Первый слайд презентации
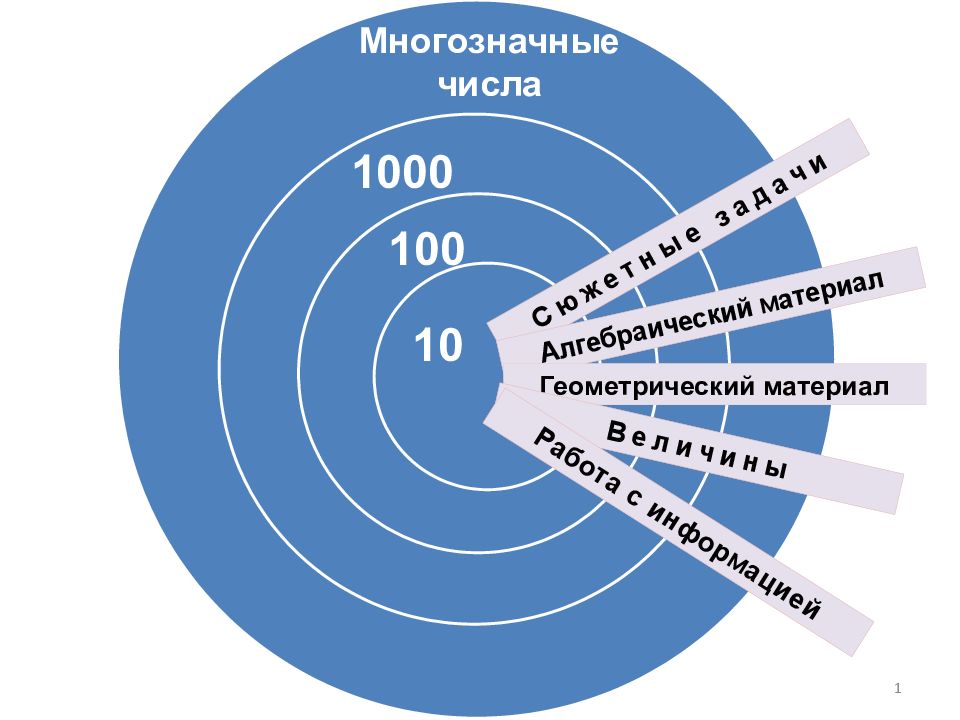
1 Сюжетные задачи Алгебраический материал Геометрический материал Величины 10 100 1000 Многозначные числа Работа с информацией
Слайд 2
Алгебраический материал изучается, начиная с 1 класса, в тесной связи с изучением арифметического материала 2
Слайд 4: Требования к знаниям и умениям
Знать: вопросы алгебраического характера (в начальном курсе математики), уровень обобщения при их раскрытии, последовательность изучения по различным программам; виды упражнений алгебраического характера; различные виды, формы и методы проверки усвоения алгебраического материала. 4
Слайд 5: Требования к знаниям и умениям
Уметь: реализовывать в практике обучения взаимосвязь арифметического и алгебраического материала; целенаправленно использовать дидактические игры, способствующие усвоению алгебраического материала; подбирать проверочные задания, составлять самостоятельные письменные работы с элементами алгебры. 5
Слайд 6: Методико-математические основы
Основные понятия темы: выражение, значение выражения, равенство, неравенство, уравнение. Способ раскрытия содержания этих понятий – показ конкретных объектов, входящих в их объем. Например: «Это выражения…», «Это равенства…», «Это неравенства…» и т.д. 6
Слайд 7: Методико-процессуальные основы
Включение алгебраического материала в курс математики начальной школы: 1. Способствует формированию абстрактного мышления, функционального мышления. 2. Повышает уровень усвоения школьниками арифметических вопросов (способствует обобщению понятий о числе, знаний об отношениях и АД). 3. Готовит детей к изучению алгебры в следующих классах. 7
Слайд 8: Содержание алгебраического материала
Две противоположные тенденции: Ранняя алгебраизация курса математики начальных классов (системы Л.В. Занкова, В.В. Давыдова и «Школа XXI века»). Введение алгебраического материала на завершающем этапе (4 класс) обучения в начальной школе («Гармония»). «Школа России» ̶ серединные взгляды (А. В. Белошистая ) 8
Слайд 9: Выражения
Выражение – это построенная по определенным правилам последовательность математических символов – чисел, букв и арифметических действий: 7, 5 + 8, 5 (3 + b ), а, 40 : 5 + 6 и т. д. 7, 5 + 8, 40 : 5 + 6 – числовые выражения 5 (3 + b ), а, 50 : к – буквенные выражения (выражения с переменной) Число, получаемое в результате выполнения действий в числовом выражении, – значение числового выражения 9
Слайд 10: Числовые выражения (что общего?)
72 – 12 : 60 8 – 10 42 : (6 – 6) 8 : 16 444 · 125 + 125 : (2 · 28 – 8 · 7) 10
Слайд 11: Числовые выражения
Существуют числовые выражения, значения которых нельзя найти (выражения не имеют смысла): 72 – 12 : 60 42 : (6 – 6) 8 – 10 444 · 125 + 125 : (2 · 28 – 8 · 7) 8 : 16 11
Слайд 12: Задачи изучения темы «Числовые выражения»
Научить учащихся читать и записывать числовые выражения. Познакомить учащихся с правилами порядка выполнения действий над числами и выработать умение находить значения числовых выражений в соответствии с этими правилами. Познакомить учащихся с тождественными преобразованиями выражений на основе свойств арифметических действий. 12
Слайд 13: Этапы ознакомления с числовыми выражениями
содержащие одно действие (1 этап); содержащие два и более арифметических действий одной ступени (2 этап); содержащие действия одной ступени и скобки (3 этап); содержащие два и более арифметических действий разных ступеней со скобками и без скобок (4 этап) Обучающихся знакомят с простейшими выражениями – суммой и разностью – в 1-м классе (понятия «числовое выражение» и «значение выражения» вводятся позже); с произведением и частным – во 2-м классе. 13
Слайд 16: Десяток»
Название арифметических действий; термины «слагаемое», «значение суммы», «уменьшаемое», «вычитаемое», «значение разности» Чтение и запись простейших математических выражений: 5 + 4 (сумма чисел «пять» и «четыре»); 7 – 2 (разность чисел «семь» и «два») 16
Слайд 17: Десяток»
Необходимость введения выражений, содержащих два действия: 6 + 2 6 + 3 6 + 4 6 + 1 + 1 6 + 2 + 1 6 + 2 + 2 Аналогично: 6 – 1 – 1; 6 – 2 – 1; 6 – 2 – 2 Выполнение предметных действий в определенном порядке и их проговаривание – вывод: арифметические действия (сложение и вычитание) в выражениях выполняются последовательно слева направо 17
Слайд 18: Знакомство с выражениями, содержащими скобки
мотивация (?), различные приемы введения (?) 18
Слайд 19: Сотня»
Обобщение знаний о правилах порядка выполнения действий. Введение правила порядка выполнения действий в выражениях, не имеющих скобок и содержащих арифметические действия разных ступеней. Разные подходы: правило в учебнике; вычислить значение выражения 20 – 10 : 2 19
Слайд 24: Тождественные преобразования
Замена данного выражения другим, значение которого равно значению данного выражения. Встречаются с 1 класса в связи со знакомством с вычислительными приемами. Выполняются поэтапно: 35 + 4 = (30 + 5) + 4 = 30 + (5 + 4) = 30 + 9. Некоторые этапы преобразования иногда не фиксируются, а выполняются устно. Ошибки при выполнении преобразований (неправильное использование правил и т. п.). 24
Слайд 25: Тождественные преобразования
25 6 + 6 + 6 = 6 ∙ 3 8 ∙ 4 + 8 = 8 ∙ 5 7 ∙ 6 – 7 = 7 ∙ 5 9 ∙ 4 = 9 + 9 + 9 + 9
Слайд 26: Тождественные преобразования
26 6 + 6 + 6 = 6 ∙ 3 8 ∙ 4 + 8 = 8 ∙ 5 7 ∙ 6 – 7 = 7 ∙ 5 9 ∙ 4 = 9 + 9 + 9 + 9
Слайд 27: Тождественные преобразования
27 Продолжи запись так, чтобы знак равенства сохранился: 76 – (20 + 4) = 76 – 20... (10 + 7) – 5 = 10 – 5... 60 : (2 ∙ 1 0) = 60 : 10... 72 : 3 = (60 + 12) : 3 = 60 : 3 + …
Слайд 28: Тождественные преобразования
конкретный смысл АД; переместительное свойство сложения и умножения; сочетательное свойство сложения и умножения; распределительное свойство умножения относительно сложения и вычитания; другие зависимости, правила и свойства арифметических действий. 28
Слайд 29: Буквенные выражения
Буквенные выражения состоят из букв, чисел, знаков действий и скобок. Предполагается, что буквы могут принимать различные значения, т. е. в выражениях они являются переменными. 29
Слайд 30: Буквенные выражения
2. Формирование понятия «переменная»: упражнения «с окошком» < 3; 6 < ; + 2 = 5, при этом необходимо подставлять в не одно, а поочередно несколько чисел 30 3. Упражнения на вычисление значений буквенных выражений при заданных числовых значениях букв, входящих в них, позволяет наблюдать зависимость между изменениями значения переменной и значениями выражения
Слайд 32: Равенства и неравенства
Если два числовых выражения соединить знаком равенства (неравенства), то получим числовое равенство (неравенство) Числовые равенства (неравенства) могут быть истинными (верными) и ложными (неверными) 32
Слайд 33: Задачи изучения темы:
Научить устанавливать отношение «больше», «меньше», «равно» между выражениями и записывать результаты сравнения с помощью знака. 2. Научить читать равенства и неравенства. 33
Слайд 34: Последовательность изучения темы
1 этап. Сравнение совокупностей предметов (прием установления взаимно-однозначного соответствия без записи результата сравнения) 2 этап. «Десяток»: сравнение чисел с опорой на наглядность, затем на свойство натурального ряда: то число больше, которое при счете называют позже «Сотня»: применение 2 способов: 1. По месту расположения в натуральном ряду. 2. На основе сравнения соответствующих разрядных чисел, начиная с высших разрядов. 34
Слайд 35: Последовательность изучения темы
3 этап. Сравнение выражений С опорой на наглядность (прием уравнивания) С опорой на вычисления (сравнение значений выражений) С опорой: на взаимосвязь между компонентами и результатом арифметического действия 20 + 5 * 20 + 6; на свойства арифметических действий (5 + 2) 3 * 5 3 + 2 3; на конкретный смысл действий. 35
Слайд 38: Уравнения
Различные подходы к определению: Предикат вида f(x) = g(x) на множестве Х, где f(x), g(x) – выражения с переменной 2. Уравнение – равенство с переменной (истинное равенство, содержащее букву) Решение уравнения – это число, при подстановке которого уравнение обращается в истинное числовое равенство; – это процесс отыскания всех таких чисел, т. е. способ его решения 38
Слайд 39: Уравнения
Существует различные способы решения : подбор (имеет ограниченное применение), использование теорем о равносильности уравнений (в начальной школе не используется), использование знаний о зависимости между компонентами и результатами арифметических действий. 39
Слайд 40: Дидактические функции способа подбора
у + 2 = 9 Формирует осознанный подход к решению уравнения, т. к. требует проверки подобранного числа. Позволяет справиться с решением нестандартных уравнений (например, х + х = х ∙ х). Предоставляет возможность упражняться в закреплении вычислительных приемов. Требует предположить, с какого числа целесообразно начинать подбор. Формирует умение «оценить», «проанализировать» записанное уравнение, что благоприятствует решению в дальнейшем уравнений с помощью правил. 40
Слайд 41: Последовательность изучения темы
1 этап. Подготовительный Два направления подготовки: Специальные упражнения с «окошечками», в результате выполнения которых учащиеся овладевают способом подбора (Какое число нужно вставить в «окошечко», чтобы получилось верное равенство… – «корень уравнения») Усвоение взаимосвязи между компонентами и результатами арифметических действий (Если из суммы вычесть одно слагаемое…) 41
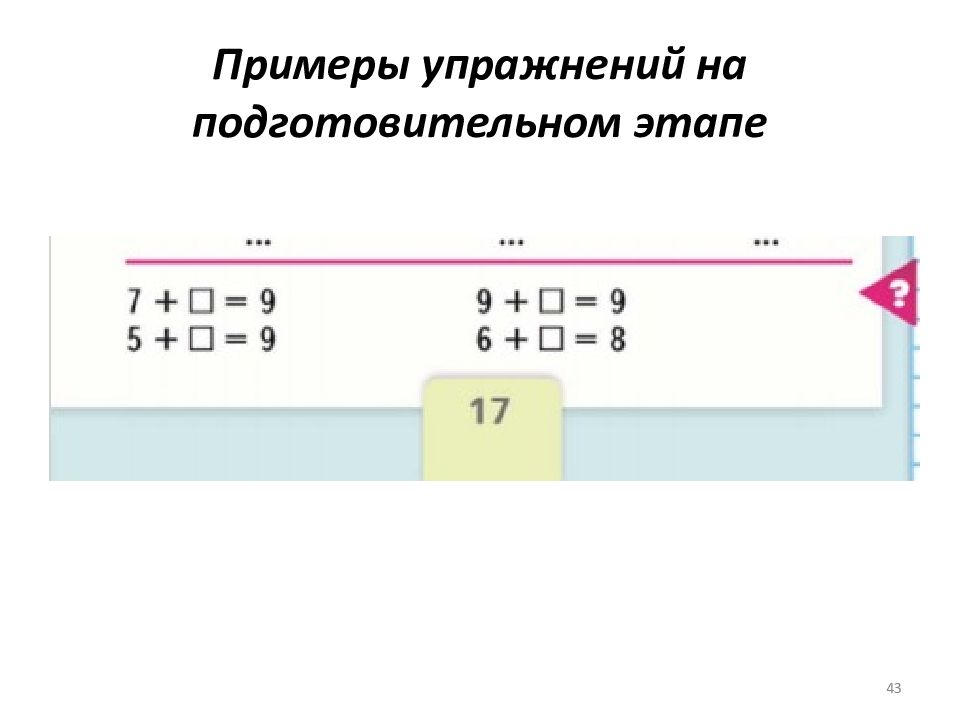
Слайд 44: Примеры упражнений на подготовительном этапе
44 К неизвестному числу прибавили 4 и получили 9. Найдите неизвестное число. Сколько надо вычесть из 6, чтобы получилось 2? Сколько надо прибавить к 3, чтобы получилось 5?
Слайд 45: 2 этап. Знакомство с понятием уравнения и овладение способами решения уравнений
замена «окошечка» латинской буквой; введение термина «неизвестное число»; узнавание уравнения среди других математических записей; решение уравнений способом подбора (сравни записи 6 + = 9 и 6 + х = 9); решение уравнений с помощью правил взаимосвязи между компонентами и результатами действий: - мотивация – ( х + 13 = 71) - поиск другого способа (с помощью учителя) 45
Слайд 50
50 1) Решите уравнения и выполните проверку. 2) Выполните проверку решенных уравнений, объясните ошибки в неверно решенных уравнениях: 20 – х = 8 х + 7 = 13 х = 20 – 8 х = 13 + 7 х = 12 х = 20 3) Составьте уравнения с числами х, 7, 10, решите их и проверьте решение. 4) Из заданных уравнений выберите и решите те, в которых неизвестное число находят вычитанием (делением). 5) Из заданных уравнений выпишите те, в которых неизвестное число равно 8. 6) Рассмотрите решение уравнения, определите, чем является неизвестное в уравнении и вставьте пропущенный знак действия: х ∙ 2 = 12 х : 2 = 12 х = 12 2 х = 12 2 7) Решите уравнения; сравните уравнения и их решения: х + 8 = 40 х ∙ 3 = 24 х – 8 = 40 х : 3 = 24.
Слайд 51
51 75 – х = 9 ∙ 7 х + (60 – 48) = 20 (х + 90) + 30 = 180 Усложнение уравнений
Слайд 54: Памятка для решения уравнений
Прочитай уравнение различными способами. Назови, что известно и что неизвестно. Вспомни, как найти неизвестное число. Найди неизвестное число, выполнив соответствующее действие. Запиши, чему равно неизвестное число. Сделай проверку. 54
Слайд 55: 3 этап. Использование уравнений при решении текстовых задач
Подготовка Запишите следующие предложения в виде равенства разными способами: 360 больше числа 40 в 9 раз, d меньше b на 17, х больше на 25, чем 12. 55
Слайд 56: Задача. В двух корзинах 37 грибов. В первой корзине 16 грибов. Сколько грибов во второй корзине?
56 37 грибов 16 гр. ? гр. х гр.
Слайд 57: Всего грибов
16 + х 37 Что можно сказать об этих выражениях? Какое уравнение можно составить? 16 + х = 37 х = 37 – 16 х = 21. 16 + 21 = 37 37 = 37 Ответ: во второй корзине 21 гриб 57
Слайд 59
59 Памятка при решении сюжетной задачи с помощью составления уравнения может быть следующей: Рассуждаю так : Подумаю, что обозначу за х. Подумаю, что буду уравнивать. Составлю два выражения, выражающих значения одной и той же величины. Записываю уравнение. Решаю уравнение. Проверяю.
Слайд 61: Развитие математической речи
Формирование умения читать выражение с помощью приема – показ образца Наиболее доступно чтение выражения в соответствии с его записью: 3 5 + 4. Другие способы чтения: к произведению чисел 3 и 5 прибавить 4, произведение 3 и 5 увеличить на 4. Затруднения в чтении выражений в соответствии с порядком действий: 3 5 + 4 «Сумма произведения чисел 3 и 5 и числа 4» 61
Слайд 62: Задание
Прочитайте выражение разными способами (используйте предложенные слова): 15 : 5 + 2 10 СУММА ПРИБАВИТЬ УВЕЛИЧИТЬ ПЛЮС 62
Слайд 64
Проверочная работа по методике изучения алгебраического материала 1. Не решая уравнений, объясните, в каком уравнении каждой пары неизвестное число больше: 70 – х = 45 и 70 – х = 25, х – 20 = 42 и х – 20 = 54, х + 15 = 40 и х + 17 = 40. 2. Укажи способы решения уравнений, которые применяют в начальной школе: подбор числа, на основе теорем о равносильности уравнений, на основе зависимости между компонентами и результатами АД, переносом слагаемых из одной части уравнения в другую. Приведите рассуждение ученика начальной школы для одного из указанных способов. 3. Выполните приведенные ниже задания и распределите их по уровню сложности (обоснуйте): А) Рассмотри два уравнения: а) c – x = m, б) s – y = m. Известно, что c < s. Поставь вместо точек знак сравнения: x … y. Обязательно докажи результат сравнения. Б) Для уравнения 385 + х = 402 выбери и обведи верное решение: 787 15 17 7 В) Запиши, как найти неизвестное число х 1) w + x = c 2) 530 – x = 620 64