Первый слайд презентации
Алгебра логики (англ. algebra of logic ) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях. Аналогию между алгеброй и логикой положил в основу своего логического учения основоположник алгебры логики английский математик и логик Дж. Буль. Любое высказывание Буль записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов. Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно — 1 или ложно — 0. Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения. Истинность или ложность высказываний зависит от истинности и ложности исходных (простых) высказываний и смысла логических операций над высказываниями . Таким образом, определение истинности некоторого логичес -кого выражения — это определение значения некоторой логической функции.
Слайд 2
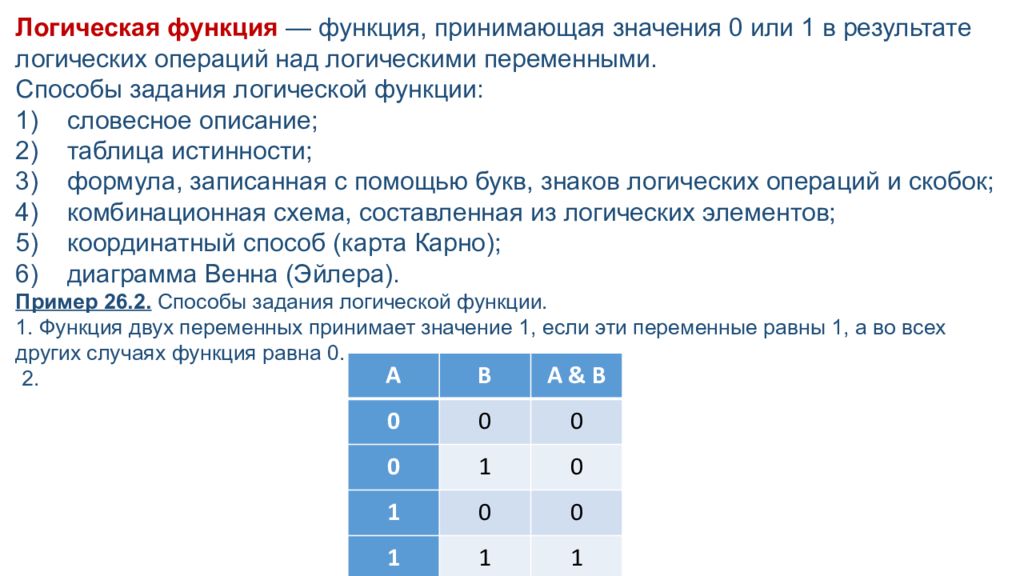
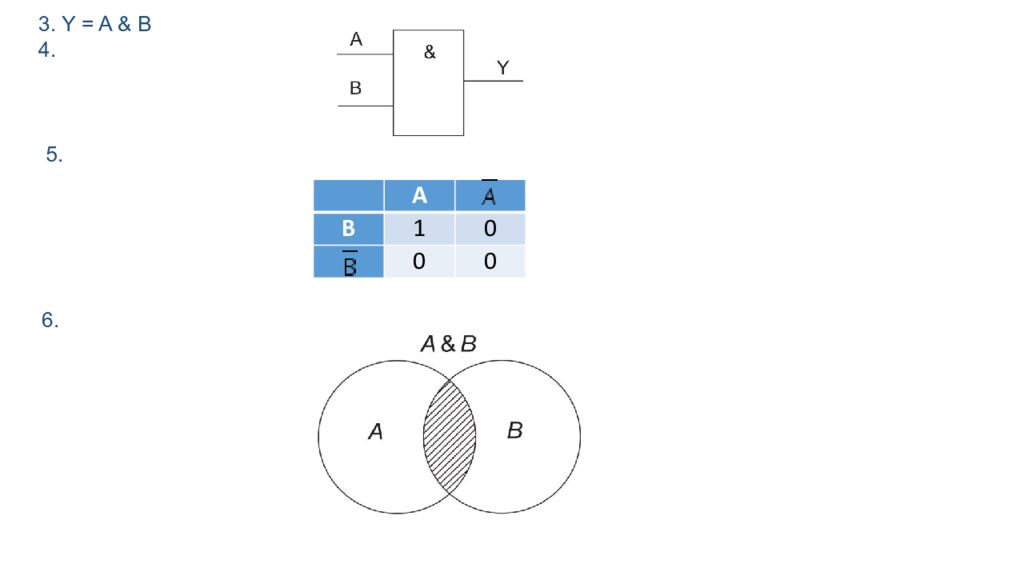
Логическая функция — функция, принимающая значения 0 или 1 в результате логических операций над логическими переменными. Способы задания логической функции: 1) словесное описание; 2) таблица истинности; 3) формула, записанная с помощью букв, знаков логических операций и скобок; 4) комбинационная схема, составленная из логических элементов; 5) координатный способ (карта Карно); 6) диаграмма Венна (Эйлера). Пример 26.2. Способы задания логической функции. 1. Функция двух переменных принимает значение 1, если эти переменные равны 1, а во всех других случаях функция равна 0. 2. A B A & B 0 0 0 0 1 0 1 0 0 1 1 1
Слайд 4
Истинность или ложность высказываний зависит от истинности и ложности исходных (простых) высказываний и смысла логических операций над высказываниями (пример 26.1). Таким образом, определение истинности некоторого логического выражения — это определение значения некоторой логической функции. Переключательная функция – такая функция от нескольких аргументов, все аргументы которой являются высказываниями, и значение которой также является высказыванием.
Слайд 5
Области применения алгебры логики: 1) в качестве средства алгоритмического описания в языках программирования для определения логических условий; 2) для формирования логических высказываний в математической логике, лингвистике, теории искусственного интеллекта; 3) в разработке и описании дискретных технических систем; 4) при анализе и синтезе логических устройств. Анализ логических устройств — это поиск аналитического выражения, которое описывает работу системы. Синтез логических устройств — обратная задача: создание технического устройства на основе математического описания средствами алгебры логики. В компьютерных устройствах применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае ток проходит, во втором — нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.
Слайд 6
Логические операции Рассмотрим основные логические операции — варианты обозначения (пример 26.3), таблицы истинности и логические элементы для каждой из логических операций (примеры 26.4 — 26.9).
Слайд 7
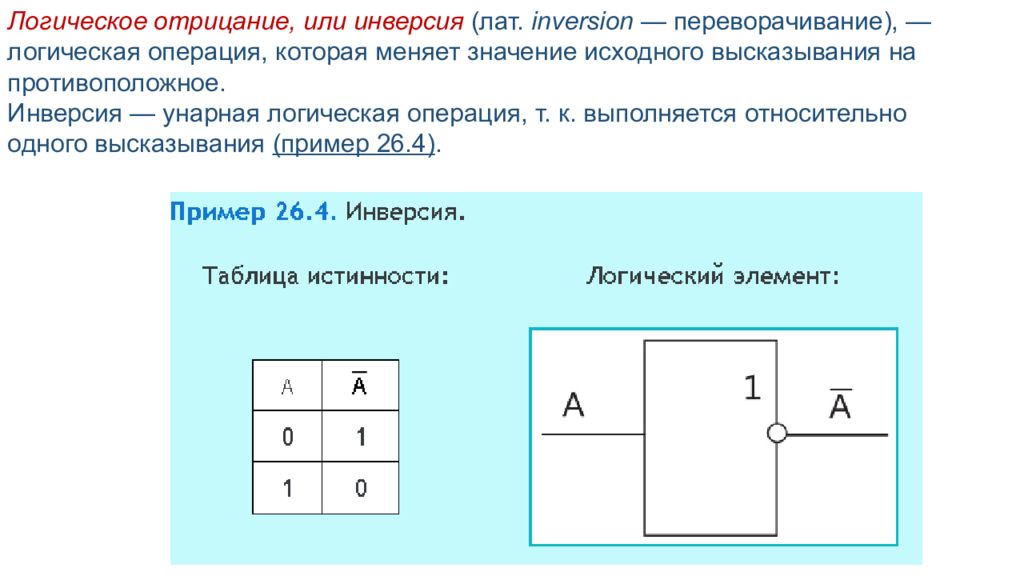
Логическое отрицание, или инверсия (лат. inversion — переворачивание), — логическая операция, которая меняет значение исходного высказывания на противоположное. Инверсия — унарная логическая операция, т. к. выполняется относительно одного высказывания (пример 26.4).
Слайд 8
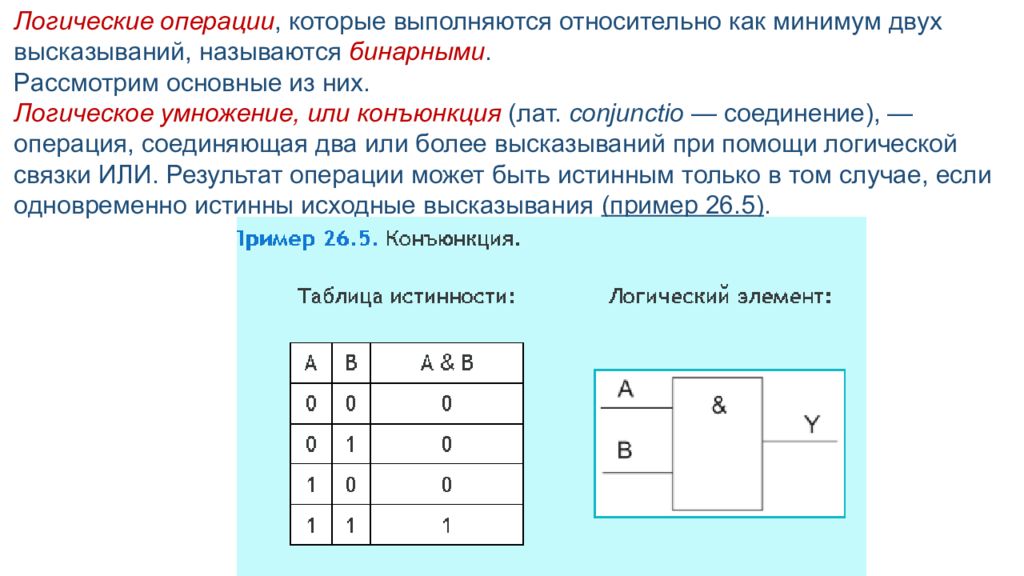
Логические операции, которые выполняются относительно как минимум двух высказываний, называются бинарными. Рассмотрим основные из них. Логическое умножение, или конъюнкция (лат. conjunctio — соединение), — операция, соединяющая два или более высказываний при помощи логической связки ИЛИ. Результат операции может быть истинным только в том случае, если одновременно истинны исходные высказывания (пример 26.5).
Слайд 9
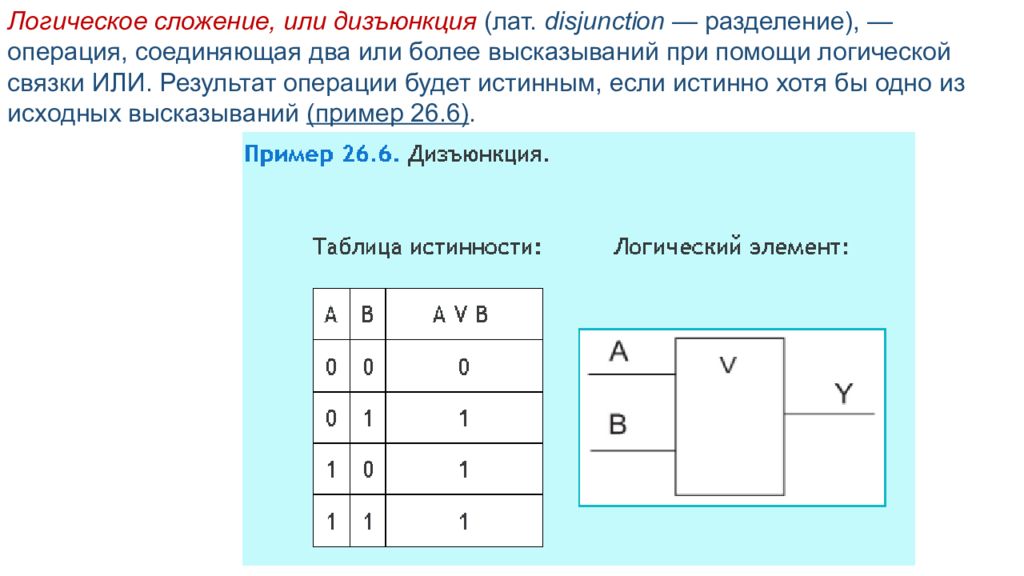
Логическое сложение, или дизъюнкция (лат. disjunction — разделение), — операция, соединяющая два или более высказываний при помощи логической связки ИЛИ. Результат операции будет истинным, если истинно хотя бы одно из исходных высказываний (пример 26.6).
Слайд 10
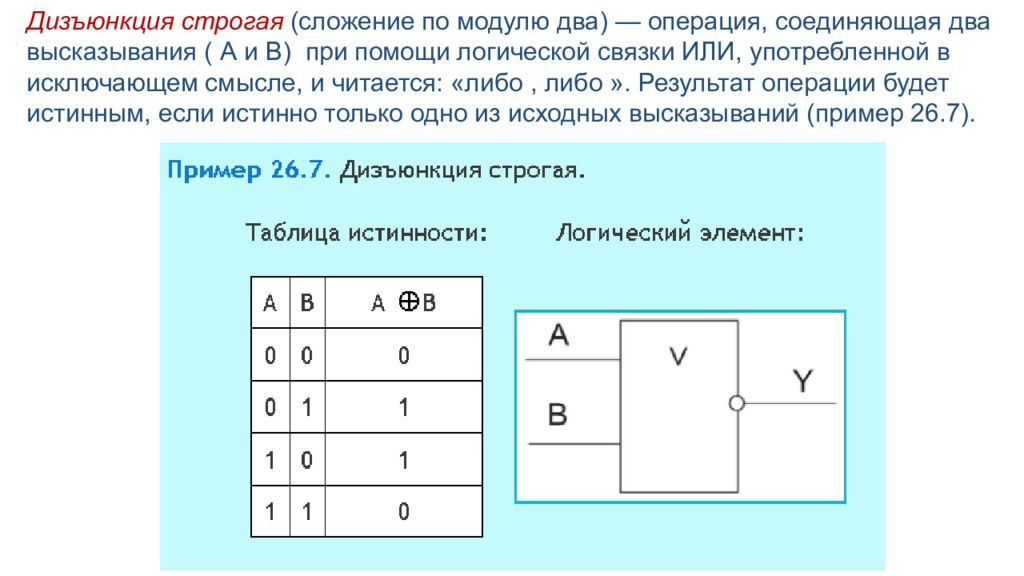
Дизъюнкция строгая (сложение по модулю два) — операция, соединяющая два высказывания ( А и В) при помощи логической связки ИЛИ, употребленной в исключающем смысле, и читается: «либо, либо ». Результат операции будет истинным, если истинно только одно из исходных высказываний (пример 26.7).
Слайд 11
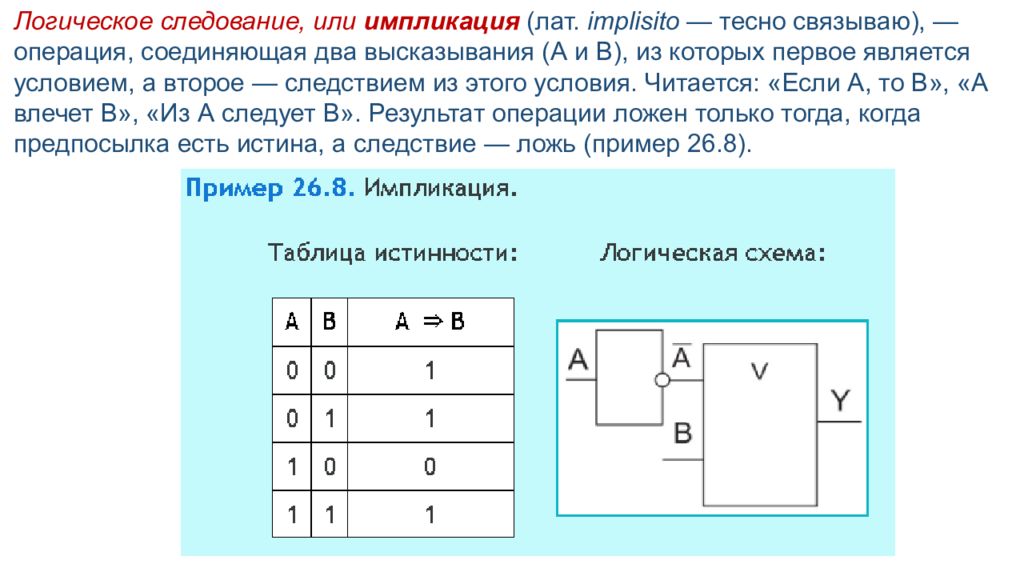
Логическое следование, или импликация (лат. implisito — тесно связываю), — операция, соединяющая два высказывания (А и В), из которых первое является условием, а второе — следствием из этого условия. Читается: «Если А, то В», «А влечет В», «Из А следует В». Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь (пример 26.8).
Слайд 12
Равнозначность, или эквивалентность (лат. aequalis — равный и valentis — имеющий силу ), — операция, позволяющая из двух высказываний (А и В) получить высказывание, которое читается так: «А равнозначно В». Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Операция эквивалентности противоположна строгой дизъюнкции и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают (пример 26.9).
Слайд 13
Логические выражения и законы логики Логическое выражение (формула) — содержит логические переменные, обозначающие высказывания, соединенные знаками логических операций. С помощью логических переменных и логических операций любое составное логическое высказывание можно формализовать, т. е. заменить логическим выражением. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу (пример 26.10). Смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Слайд 14
В логических выражениях должен соблюдаться следующий порядок выполнения операций (пример 26.11) : 1) действия в скобках; 2) инверсия; 3) конъюнкция; 4) дизъюнкция; 5) импликация; 6) эквивалентность.
Слайд 15
Значение логического выражения можно определить, построив таблицу истинности для этого выражения. Для построения таблицы истинности необходимо выполнить следующие действия (пример 26.12): 1) подсчитать число переменных в выражении ( n ); 2) подсчитать число логических операций в выражении ( p ); 3) установить последовательность выполнения логических операций в выражении с учетом скобок и приоритетов; 4) вычислить количество столбцов в таблице ( n + p ); 5) заполнить шапку таблицы, включив в нее переменные и операции в соответствии с установленной в п. 3 последовательностью; 6) вычислить количество строк в таблице ( m = 2 n ); 7) записать в таблице все возможные наборы значений переменных; 8) заполнить таблицу по столбцам, выполняя логические операции в соответствии с установленной в п. 3 последовательностью.
Слайд 16
Для преобразования и упрощения формул в алгебре логики производятся эквивалентные преобразования, опирающиеся на основные логические законы (пример 26.13). Некоторые из этих законов формулируются и записываются так же, как аналогичные законы в арифметике и алгебре, другие выглядят непривычно.
Слайд 17
Доказано, что для представления любой логической функции достаточно трех операций: конъюнкции, дизъюнкции и отрицания. Т.е. любую логическую формулу можно путем преобразований и упрощений привести к формуле, содержащей только эти три основные логические операции. Пример 26.14. Упростить логическое выражение . и построить логическую схему, соответствующую результату. Выполним эквивалентные преобразования выражения в соответствии с законами логики: Импликации. Де Моргана. Инволюции. Дистрибутивности.
Слайд 18
Основные теоремы и положения алгебры логики. Принцип двойственности. Запишем правила выполнения операций ИЛИ и И, расположив строчки И в обратном (снизу вверх) порядке: Сравним построчно операции ИЛИ и И. Если заменить в строках ИЛИ и И все 0 на 1, все 1 на 0 и знаки дизъюнкции на знаки конъюнкции, то правила меняются местами: строка ИЛИ превращается в строку И и наоборот. В этом состоит принцип двойственности, который в общем виде записывается так:
Слайд 19
Для преобразования формул алгебры логики с целью их минимизации использу-ются, как и в обычной алгебре, скобки, а если их нет, то сначала выполняется отрицание (инверсия) над отдельными переменными, затем логическое умножение (конъюнкция) и наконец логическое сложение (дизъюнкция). Однако, если черта (знак инверсии) стоит над совокупностью букв и знаков, то она выполняется в последнюю очередь. В процессе преобразования формул используются также теоремы алгебры логики.
Слайд 20
Теоремы для одной переменной ( легко проверяемые подстановкой А=1 и А=0): Эти теоремы (как и последующие) остаются справедливыми и для случая, если под А понимать не только одну переменную, но и целое выражение. Теоремы для двух и более переменных:
Слайд 21
Если теоремы 10, 11 очевидны и совпадают с правилами обычной алгебры, то очевидность теоремы 12 б (как и ряда следующих теорем) следует из принципа двойственности. Заменим в левой и правой частях теоремы 12 а все переменные их отрицаниями и поменяем знаки конъюнкции и дизъюнкции друг на друга, получим:
Слайд 24
Булевы функции Значение булевой функции F, как результат выполнения логических операций над двоичными переменными — аргументами А, В, С,..., зависит от значения аргументов. Задать булеву функцию — значит указать значения, которые принимает функция (т.е. 0 или 1) при всех возможных комбинациях значений аргументов. Таблица, в которой построчно указываются все возможные сочетания аргументов и значения, которые булева функция принимает при каждом сочетании, называется таблицей истинности. Так, например, функции ИЛИ и И имеют только два аргумента А и В, поэтому имеется четыре возмож-ные комбинации их значений, которые представлены в их таблице истинности (см. табл. 3.3). Каждую конкретную комбинацию аргументов называют набором. Для краткости набор записывают в виде двоичного числа, цифрами которого являются значения аргументов. Для п аргументов существует N = 2 n наборов. Если неизвестно, какие значения принимает функция на всех наборах аргументов, то она называется недоопределенной, или не полностью (частично) определенной, а комбинации аргументов, для которых функция не определена, — запрещенными наборами. Значения функции на запрещенных наборах можно задать по своему усмотрению (доопределить функцию). Этот прием используется при минимизации функций. После того как таблица истинности составлена, находят алгебраическую форму этой логической функции. На следующем этапе функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующих электрических схем. Логические функции записывают, как правило, в дизъюнктивной нормальной форме.
Слайд 26
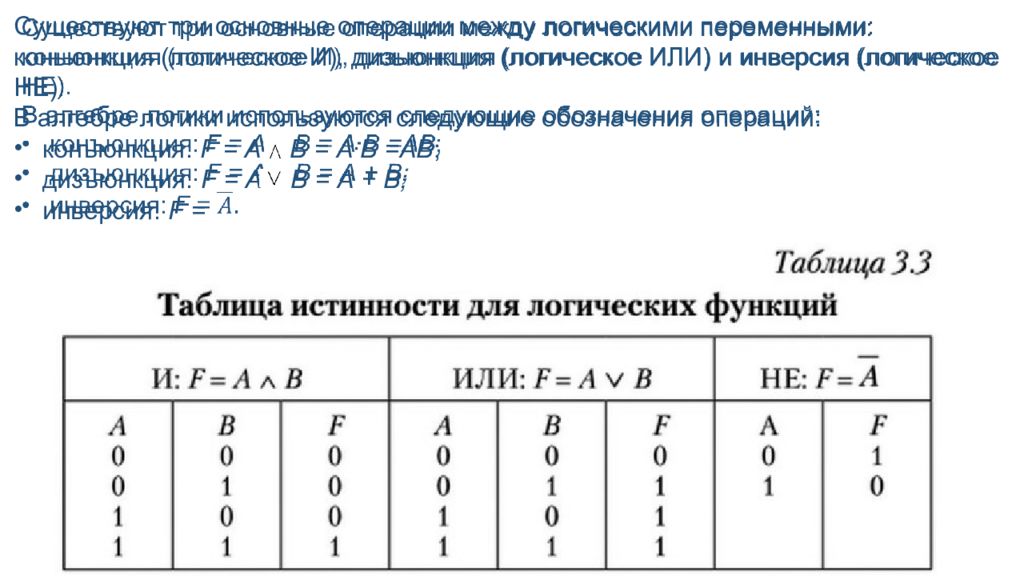
Существуют три основные операции между логическими переменными: коньюнкция (логическое И), дизьюнкция (логическое ИЛИ) и инверсия (логическое НЕ). В алгебре логики используются следующие обозначения операций: конъюнкция: F = А В = А∙В =АВ ; дизъюнкция: F = А В = А + В; инверсия: F =
Слайд 27
Как следует из табл. 3.3, для конъюнкции — логического И — F только тогда равна 1, когда ее аргументы А и В равны 1. При дизъюнкции (логическом ИЛИ) F равна 1 тогда, когда А или В равны 1. Отсюда и следуют названия этих функций. Обе эти функции можно распространить на сколь угодно большое число переменных. Инверсия — логическая функция только одной переменной.