Первый слайд презентации
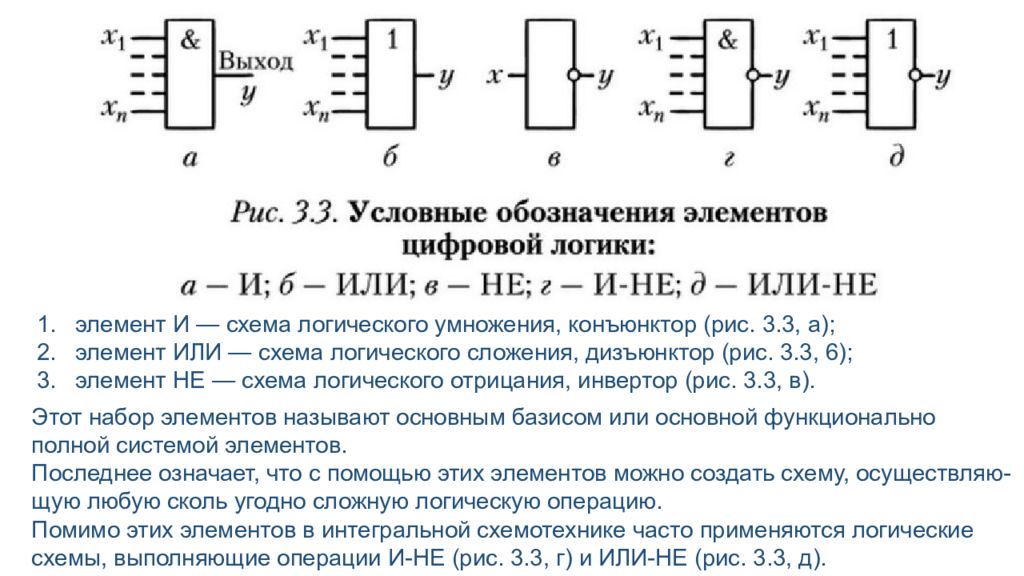
Алгебра логики и цифровые электронные схемы Как можно представить логические функции с помощью электрических схем? Логические переменные могут иметь только два дискретных значения. Следует обратить внимание на схемы, которые могут находиться в двух легко различимых состояниях. Такими схемами являются электрические переключающие схемы, выполняемые на основе транзисторных ключей. Для представления логических переменных в цифровой схемотехнике используют электрическое напряжение, имеющее два различных уровня: высокий, близкий по уровню к напряжению питания (транзистор закрыт), низкий, близкий к потенциалу корпуса (транзистор открыт). Этим уровням можно поставить в соответствие состояния логических «1» и «0». Если высокий уровень напряжения соответствует логической «1», а низкий — «0», такая система обозначений называется позитивной логикой. Если высокий уровень —« 0, а низкий – «1 », система называется негативной логикой. В соответствии с тремя операциями алгебры логики в схеме цифровых устройств используют следующие логические элементы, входные переменные которых часто обозначают через х i а выходные через y :
Слайд 2
элемент И — схема логического умножения, конъюнктор (рис. 3.3, а); элемент ИЛИ — схема логического сложения, дизъюнктор (рис. 3.3, 6); элемент НЕ — схема логического отрицания, инвертор (рис. 3.3, в). Этот набор элементов называют основным базисом или основной функционально полной системой элементов. Последнее означает, что с помощью этих элементов можно создать схему, осуществляю- щую любую сколь угодно сложную логическую операцию. Помимо этих элементов в интегральной схемотехнике часто применяются логические схемы, выполняющие операции И-НЕ (рис. 3.3, г) и ИЛИ-НЕ (рис. 3.3, д).
Слайд 3
Информация, поступающая в цифровое устройство, представляет дискретный (т.е. сос-тоящий из нулей и единиц) сигнал (код). На передачу сигнала отводится конечный отрезок времени, называемый тактом работы устройства. Если за один такт в устройство передается один из разрядов двоичного числа, то устройство работает с последовательным кодом, если же за один такт передается все двоичное число одновременно, то устройство работает с параллельным кодом. В общем случае на вход цифрового устройства поступает множество двоичных переменных Х ( х 1, х 2,..., x n ), а с выхода снимается множество двоичных переменных Y ( y 1, y 2,..., у s ). При этом устройство осуществляет (реализует) определенную связь (логическую функцию) между входными и выходными переменными. Цифровые устройства делят на комбинационные и последовательностные.
Слайд 4
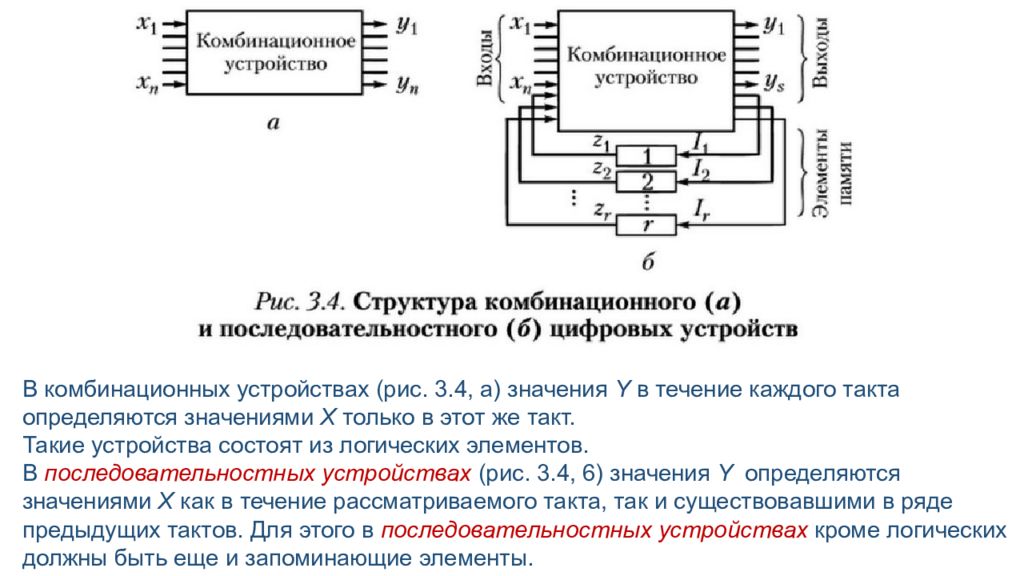
В комбинационных устройствах (рис. 3.4, а) значения Y в течение каждого такта определяются значениями Х только в этот же такт. Такие устройства состоят из логических элементов. В последовательностных устройствах (рис. 3.4, 6) значения Y определяются значениями Х как в течение рассматриваемого такта, так и существовавшими в ряде предыдущих тактов. Для этого в последовательностных устройствах кроме логических должны быть еще и запоминающие элементы.
Слайд 5
При этом память устройства может охватывать не бесконечно большое, а конечное число тактов. Поэтому цифровые (дискретные) устройства с памятью называют конечными автоматами, которыми являются все ЭВМ. Подобно входным и выходным переменным, переменные, сохраняемые в памяти устрой- ства, тоже двоичные и зависят от значений входных переменных в предыдущих тактах. Любое дискретное устройство и составляющие его элементы и узлы осуществляют ту или иную булеву функцию над двоичными входными переменными. Известно, что булеву функцию можно задать тремя способами: содержательно (путем словесного описания), таблично алгебраически. Наиболее часто для описания работы дискретных устройств пользуются табличной формой. Таблицы, показывающие связь между входными и выходными переменными комбинационных устройств, так же как и в алгебре логики, называют таблицами истинности, а алгебраическая форма этих связей представляет систему алгебраических функций :
Слайд 6
В последовательностных устройствах выходные переменные у i ; зависят не только от входных сигналов х k, но и от сигналов элементов памяти, поступающих в этот же такт. При анализе и синтезе последовательностные устройства делят на комбинационную часть и элементы памяти. Обозначим два следующих друг за другом такта работы автомата как t и ( t + 1). Состояние элементов памяти в ( t + 1)-й такт определяется множествами как входных сигналов, так и сигналов на выходах элементов памяти в предыдущий такт t, т.е. z i t +1 = >φ i (х 1, х 2, …, х n, I 1, I 2, …, I r ) t. Это выражение называют функцией переходов. Функции переходов и выходов последовательностных устройств могут выражаться таблицами переходов и выходов. Поскольку эти таблицы описывают работу последовательностного устройства, т.е. процесс его переключения, они называются также таблицами переключений. Реальные электрические схемы всегда инерционны, и между моментом изменения сигналов на входе схемы и моментом появления соответствующего сигнала на выходе всегда проходит пусть и небольшое (наносекунды), но конечное время.
Слайд 7
Таблицы и алгебраические функции описывают лишь установившийся режим, т.е. в статике. В динамической же части такта связь между переменными может отличаться от режима статики. Это явление называют переходным состоянием (гонками в автоматах). Если его не учитывать, то спроектированное устройство может работать с ошибками. Для борьбы с гонками в автоматах используют синхронизацию работы электронных схем. В соответствии с этим цифровые устройства разделяются на: асинхронные; синхронные. В асинхронных изменение входных сигналов сразу влечет за собой соответствующее изменение выходных сигналов (конечно, после окончания переходных процессов в электронных схемах). В синхронных изменение выходных сигналов происходит только после подачи синхронизирующих (тактовых) импульсов, управляющих работой автомата. Комбинационные части автоматов являются асинхронными. Значит, на их выходе могут появляться гонки, которые приводят к сбоям (ошибкам), если элементы памяти автомата будут управляться непосредственно выходными сигналами комбинационной части.
Слайд 8
Такие автоматы называют асинхронными, и в них существует опасность сбоев. В синхронных автоматах элементы памяти изменяют свое состояние только с приходом внешнего тактового импульса, т.е. когда все переходные процессы в комбинационной части закончатся и на ее выходах установятся сигналы, соответствующие входным. Поэтому опасности сбоев из-за гонок в таких автоматах нет.
Слайд 9
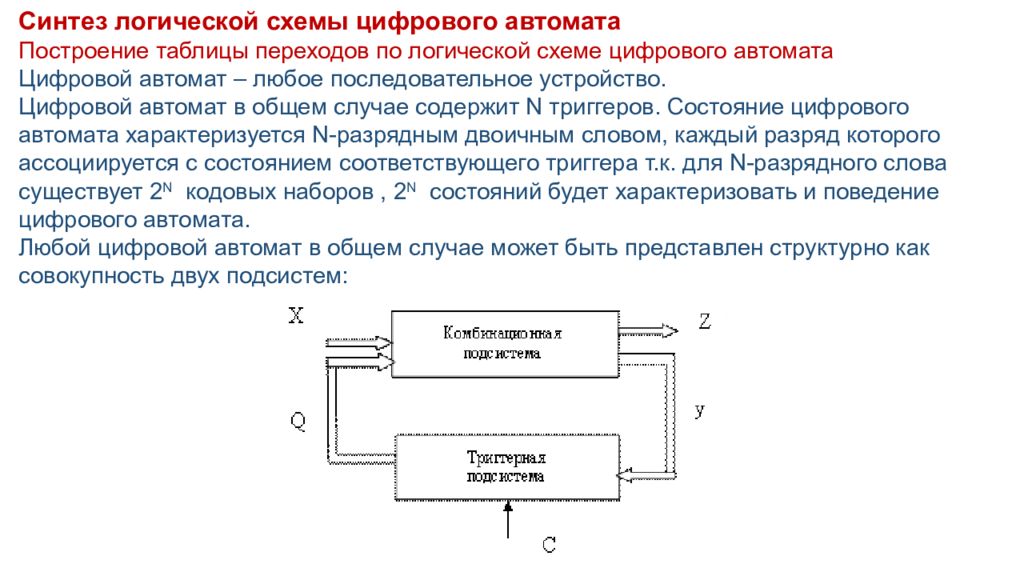
Синтез логической схемы цифрового автомата Построение таблицы переходов по логической схеме цифрового автомата Цифровой автомат – любое последовательное устройство. Цифровой автомат в общем случае содержит N триггеров. Состояние цифрового автомата характеризуется N-разрядным двоичным словом, каждый разряд которого ассоциируется с состоянием соответствующего триггера т.к. для N-разрядного слова существует 2 N кодовых наборов, 2 N состояний будет характеризовать и поведение цифрового автомата. Любой цифровой автомат в общем случае может быть представлен структурно как совокупность двух подсистем:
Слайд 10
Поведение структуры описывается 4-мя группами сигналов: Х – кодовое слово входного воздействия Z – кодовое слово, обеспечивающее требуемый порядок смены состояний цифрового автомата Q- кодовое слово, характеризующее состояние цифрового автомата. Сигнал С-синхронизации, инициирующий перекл -е триггера в триггерной подсистеме. Формирование С, как правило, непосредственно связано с алгоритмом работы устройства, в любом конкретном случае оговаривается отдельно. При проектировании цифрового аппарата необходимо определить объем памяти или число триггеров, обеспечивающих заданный алгоритм работы цифрового аппарата: n ≥log2 M , где n- ближайшее большое число, М- число необходимое из условий работы состояний цифрового аппарата. Необходимое число состояний цифрового аппарата М может быть определено как максимальное число значений выходного сигнала, которое может существовать при одном значении входного сигнала. Работа цифрового аппарата может быть описана любой формой записи. Чаще для первичной постановки задачи используют словесное описание и таблицы состояний (переходов) или графы переходов (схемы состояния) т.к. все эти формы описывают один и тот же алгоритм работы, они легко преобразуется одна в другую.
Слайд 11
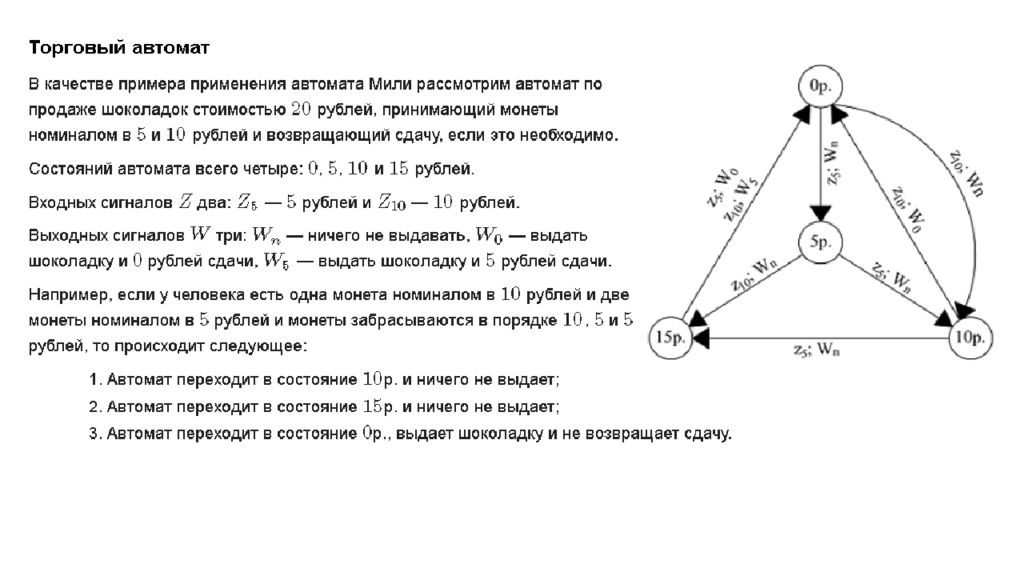
Пример: Автомат для формирования сигнала перегрузки пассажирского лифта. Допустим: Одновременно в кабине лифта, вмещающей 6 человек, могут транспортироваться не более 3-х человек. Если число пассажиров превышает 3-х, то должен выдаваться сигнал на блокировку работы лифта (сигнал перегрузки). Входным сигналом является двоичный код, 1 в нулевом разряде который обозначает больше числа пассажиров на 1, что фиксируется датчиком, а 1 в первом разряде – уменьшение пассажиров на 1. Решение: По словесному описанию алгоритма на входе цифрового автомата возможно действие трех различных входных сигналов: число пассажиров в лифте остается неизменно число пассажиров в лифте больше на одного число пассажиров в лифте меньше на одного. Таблица состояний включает: - G+1 столбец, где G – число различных входных сигналов, которые могут быть на входе цифрового автомата, т.е. 3+1=4 столбца. - 2 n строк. Число необходимых состояний М определяется из анализа работы устройства: - лифт пуст - в лифте 1 чел - в лифте 2 чел - в лифте 3 чел - в лифте 4 чел - в лифте 5 чел - в лифте 6 чел.
Слайд 12
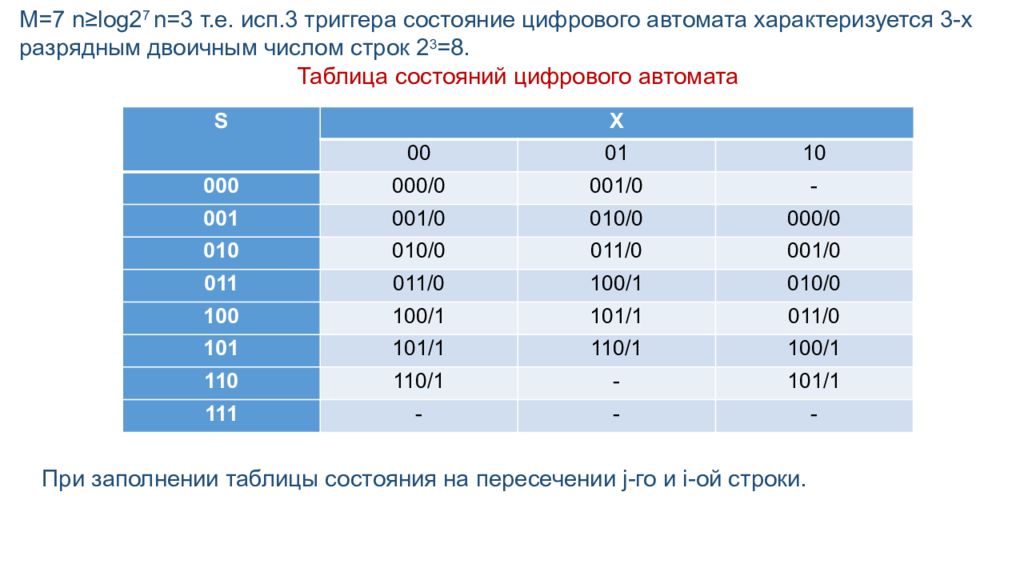
М=7 n≥log2 7 n=3 т.е. исп.3 триггера состояние цифрового автомата характеризуется 3-х разрядным двоичным числом строк 2 3 =8. Таблица состояний цифрового автомата S X 00 01 10 000 000/0 001/0 - 001 001/0 010/0 000/0 010 010/0 011/0 001/0 011 011/0 100/1 010/0 100 100/1 101/1 011/0 101 101/1 110/1 100/1 110 110/1 - 101/1 111 - - - При заполнении таблицы состояния на пересечении j- го и i-ой строки.
Слайд 13
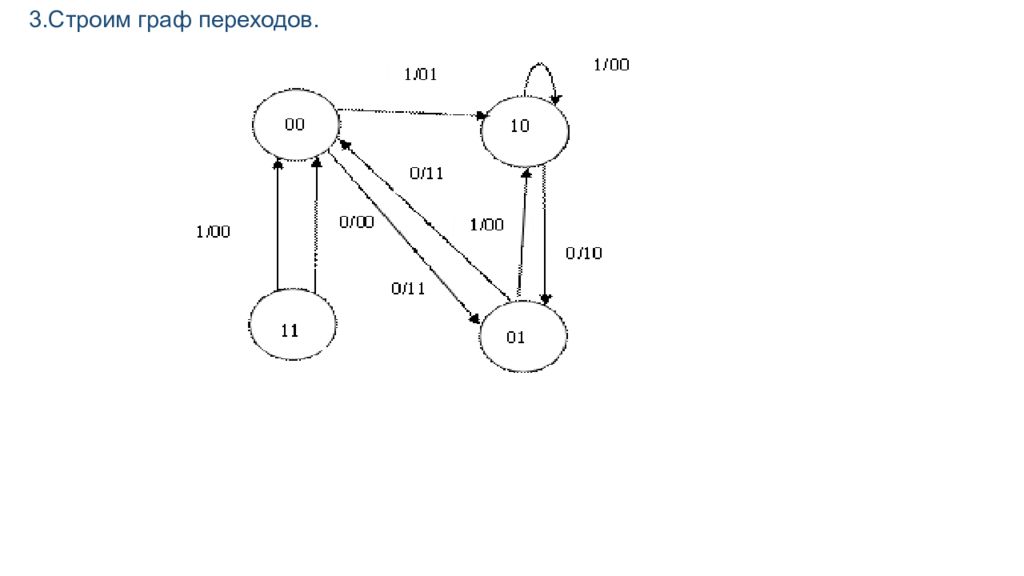
Записывается дробь: - в числителе записывается состояние, в которое попадает цифровой автомат после прихода очередного импульса С, если он находился в i-ом состоянии и на его вход действовал j- ый входной сигнал - в знаменателе указывается текущее значение выходного сигнала существующего в цифровой автомат до прихода очередного импульса С при нахождении его в i-ом состоянии при действии j- го входного сигнала. Граф переходов – представляет собой графическую интерпретацию работы цифрового автомата. Им удобно пользоваться, если при первичном описании до конца не рассмотрен весь алгоритм работы и нельзя определить число М возможных состояний. При числе состояний 2 n >16 граф нагляднее таблицы. Каждое состояние цифрового автомата изображено в виде окружности с указанием N или кода соответствующего состояния. Переход от одного состояния к другому изображено в виде стрелки. Над стрелкой записывается дробь: - в числителе которой, дано значение входного сигнала, под действием которого, при очередном импульсе С, произойдет указанный переход. - в знаменателе записывается текущее значение выходного сигнала, соответствующее указанным состоянию и значению выходного сигнала.
Слайд 14
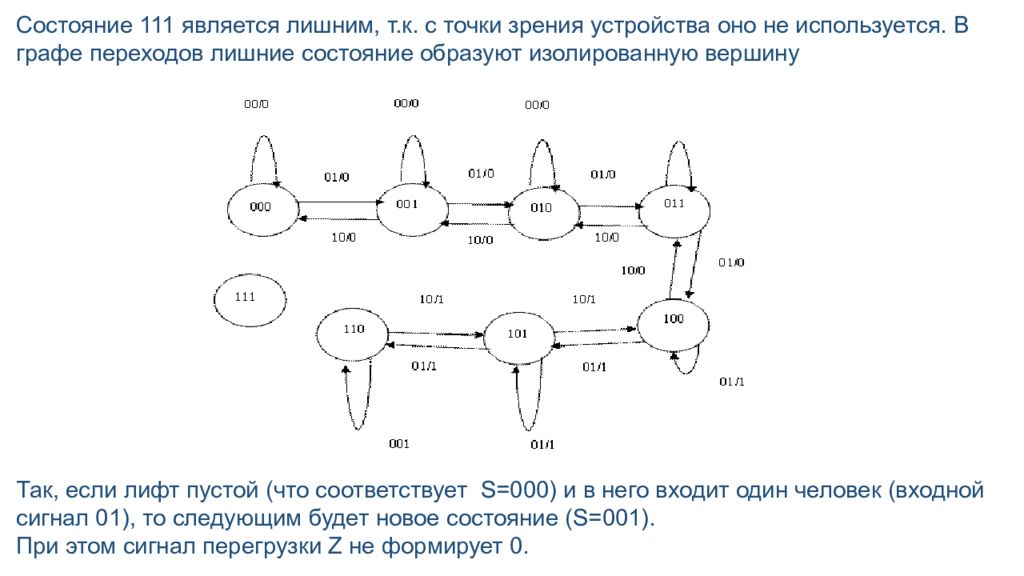
Состояние 111 является лишним, т.к. с точки зрения устройства оно не используется. В графе переходов лишние состояние образуют изолированную вершину Так, если лифт пустой (что соответствует S=000) и в него входит один человек (входной сигнал 01), то следующим будет новое состояние (S=001 ). При этом сигнал перегрузки Z не формирует 0.
Слайд 15
Правила синтеза логической схемы цифрового автомата. По условию работы цифрового автомата определяют число необходимых состояний и требуемый объем памяти его триггерной подсистемы Выполняют формальное описание алгоритма работы цифрового автомата, т.е. составляют таблицу состояний или граф переходов. Выбирают тип триггера для реализации триггерной подсистемы. Используя формализованный алгоритм работы цифрового автомата и таблицы истинности для выбранного типа триггера, составляют расширенную таблицу переходов. Число строк таблицы равно максимальному числу значений входного сигнала комбинационной подсистемы. Число столбцов таблицы 5: Х – входной сигнал; Qn – текущее состояние; Qn+1 – следующее состояние; Y – входные сигналы на информационных входах триггеров; Z – выходные сигналы. Используя расширенную таблицу переходов, минимизируют ФАЛ (функции алгебры логики), описывающие комбинационную подсистему цифрового автомата. По полученным ФАЛ строят логическую схему цифрового автомата.
Слайд 16
Пример: Вернемся к нашему примеру. 1 и 2 пункты уже сделаны, выберем тип триггера. Нет однозначных рекомендаций по выбору типа триггера, чтобы в дальнейшем получить наиболее простую техническую реализацию. Однако, при выборе триггера, информационные сигналы, которые содержат большое число неопределенных значений входного сигнала, структура цифрового аппарата получается более проста. Рекомендуется предпочтение отдавать JK,RS и: 3 пункт: выбираем JK-Триггер 4 пункт: получение расширенной таблицы истинности По таблице состояний – на вход комбинационной подсистемы действующих 5 переменных: х1,х0 – входные управляющие сигналы, Q2 Q1 Q0 – вых. сост. триггерной подсистемы. Расширенная таблица истинности должна содержать 2 5 =32 строки, что усложняет процедуру проектирования. Для упрощения проектирования необходимо понизить число входных переменных комбинационной подсистемы. Обратимся к таблице состояний. Объем памяти понижать не можем, т.к. он определяется числом состояний М.
Слайд 17
Пути упрощения данного алгоритма: 2-й способ: 2-х разрядный код воздействия отражает всего 2 ситуации: человек вошел в лифт (01 ) человек вышел (10 ). Код 11 невозможен по условиям работы устройства. Код 00 при нем по каждому сигналу С происходит подтверждение текущего состояния и выходных сигналов устройства. Того же эффекта можно добиться, если нет изменения состояния. Сигнал С будет отсутствовать и триггер будет в режиме хранения информации. Тогда, используя асинхронный триггер, внешнее воздействие на устройство можно представить одноразрядным двоичным кодом. Число строк ниже в 2 раза: 2 4 =16
Слайд 18
1 способ: Присвоение входным воздействиям различного приоритета, так чтоб устройство при поступлении одновременно нескольких входных сигналов выбирало бы наиболее важный. Так, по условию надо формировать сигнал перегрузки. Увеличение числа пассажиров (х0=1) – имеет повышенный приоритет. Таблица истинности должна рассматривать все возможные ситуации в работе, для однозначного определения поведения устройства в любых аварийных ситуациях. Хотя по условию работы входной сигнал 11 не возможен, по таблице истинности должны рассмотреть все варианты. При появлении кода 11 устройство должно реагировать, как на сигнал 01. Тогда в данном случае можно сократить число строк на 8.
Слайд 19
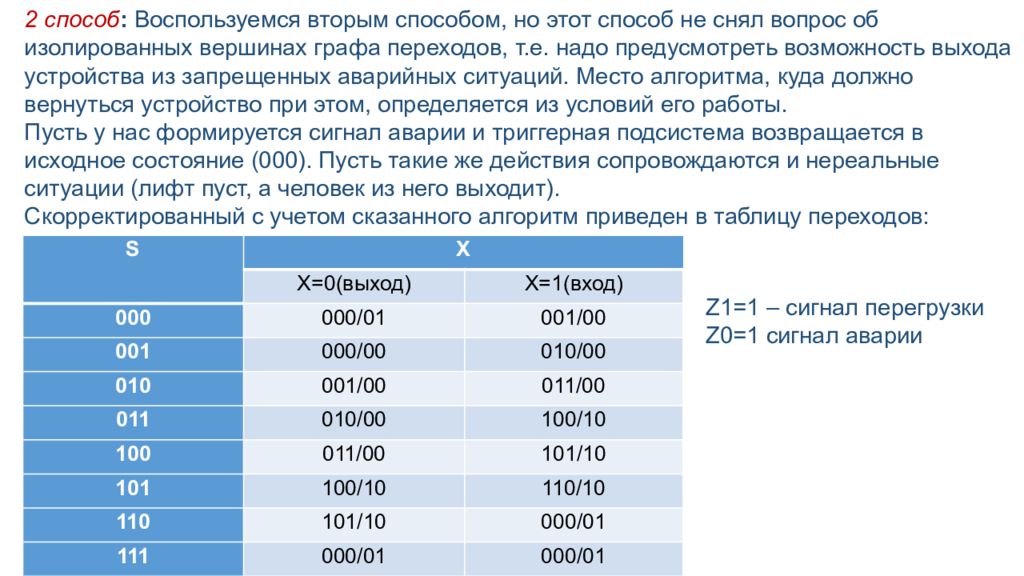
2 способ : Воспользуемся вторым способом, но этот способ не снял вопрос об изолированных вершинах графа переходов, т.е. надо предусмотреть возможность выхода устройства из запрещенных аварийных ситуаций. Место алгоритма, куда должно вернуться устройство при этом, определяется из условий его работы. Пусть у нас формируется сигнал аварии и триггерная подсистема возвращается в исходное состояние (000). Пусть такие же действия сопровождаются и нереальные ситуации (лифт пуст, а человек из него выходит). Скорректированный с учетом сказанного алгоритм приведен в таблицу переходов: S X Х=0(выход) Х=1(вход) 000 000/01 001/00 001 000/00 010/00 010 001/00 011/00 011 010/00 100/10 100 011/00 101/10 101 100/10 110/10 110 101/10 000/01 111 000/01 000/01 Z1=1 – сигнал перегрузки Z0=1 сигнал аварии
Слайд 20
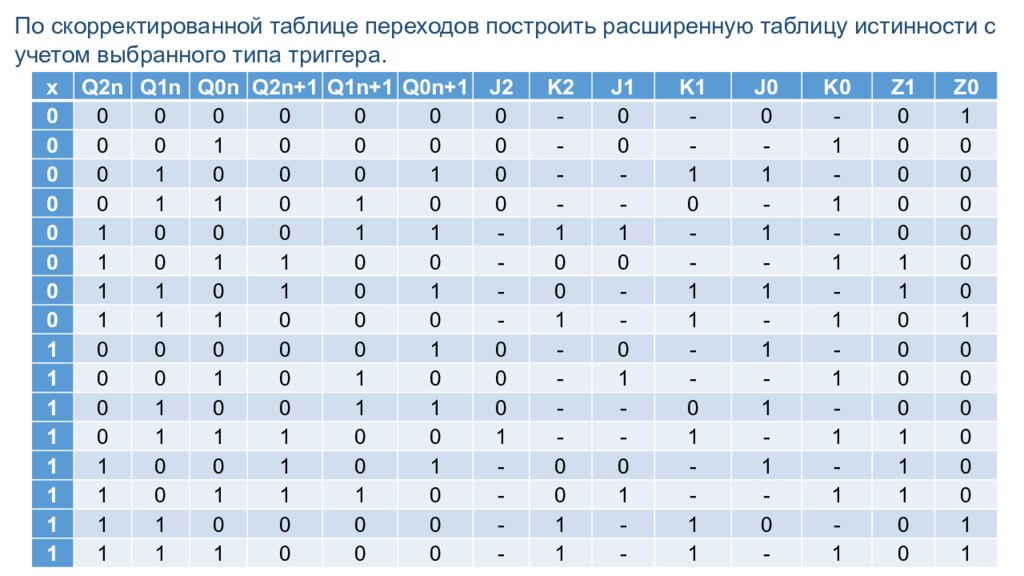
По скорректированной таблице переходов построить расширенную таблицу истинности с учетом выбранного типа триггера. х Q2n Q1n Q0n Q2n+1 Q1n+1 Q0n+1 J2 K2 J1 K1 J0 K0 Z1 Z0 0 0 0 0 0 0 0 0 - 0 - 0 - 0 1 0 0 0 1 0 0 0 0 - 0 - - 1 0 0 0 0 1 0 0 0 1 0 - - 1 1 - 0 0 0 0 1 1 0 1 0 0 - - 0 - 1 0 0 0 1 0 0 0 1 1 - 1 1 - 1 - 0 0 0 1 0 1 1 0 0 - 0 0 - - 1 1 0 0 1 1 0 1 0 1 - 0 - 1 1 - 1 0 0 1 1 1 0 0 0 - 1 - 1 - 1 0 1 1 0 0 0 0 0 1 0 - 0 - 1 - 0 0 1 0 0 1 0 1 0 0 - 1 - - 1 0 0 1 0 1 0 0 1 1 0 - - 0 1 - 0 0 1 0 1 1 1 0 0 1 - - 1 - 1 1 0 1 1 0 0 1 0 1 - 0 0 - 1 - 1 0 1 1 0 1 1 1 0 - 0 1 - - 1 1 0 1 1 1 0 0 0 0 - 1 - 1 0 - 0 1 1 1 1 1 0 0 0 - 1 - 1 - 1 0 1
Слайд 21
По таблице истинности записываем ФАЛ: По ФАЛ можно построить принципиальную схему: Берем 3 триггера и заводим на каждый вход соответствующие функции. Схема большая приводить не будем.
Слайд 23
Построение таблицы переходов по логической схеме цифрового автомата Данная задача является обратной к выше рассматриваемой и позволяет по известной схеме цифрового автомата определить его реакцию на заданную последовательность входных сигналов. Реакцию на последовательность входных сигналов можно определить по таблице или по графу переходов цифрового автомата. Получить их можно по методике: По логической схеме цифрового автомата записывают ФАЛ, связывающее его выходные сигналы и сигналы на информационных входах Т с входными сигналами и кодами состояний триггерной подсистемы. Строят расширенную таблицу истинности. Записываются все возможные комбинации входных сигналов и кодов состояния триггерной подсистемы По ФАЛ для записанных входных воздействий комбинационной подсистемы отыскивают соответствующие значения выходных сигналов и сигналов на информационных входах триггеров; По известным информационным сигналам триггеров и таблице истинности переходов находят коды следующих состояний триггерной подсистемы По расширенной таблице истинности составляют таблицу состояний или граф переходов цифрового автомата.
Слайд 24
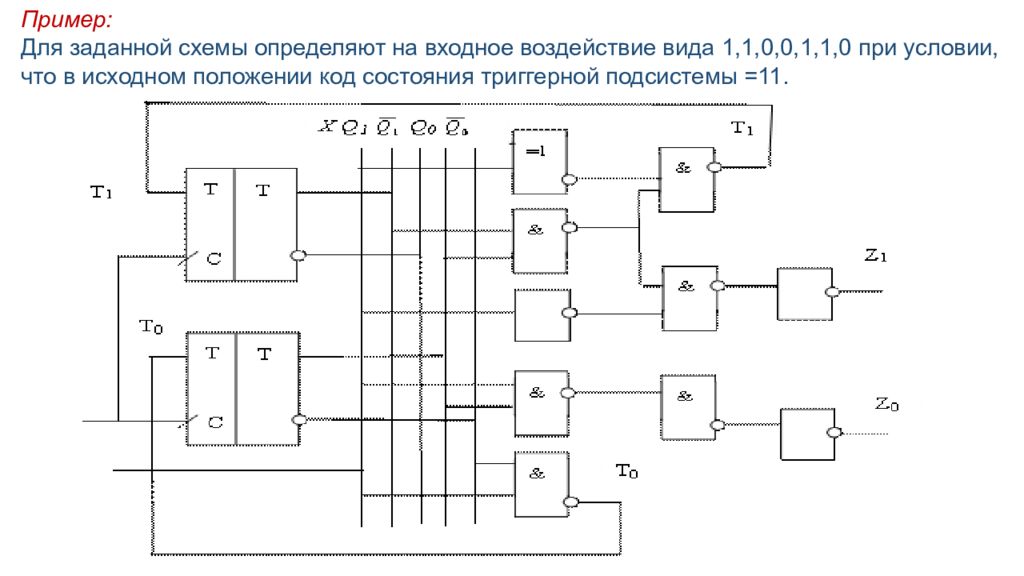
Пример: Для заданной схемы определяют на входное воздействие вида 1,1,0,0,1,1,0 при условии, что в исходном положении код состояния триггерной подсистемы =11.
Слайд 25
Решение : 1. Записываем ФАЛ для выходных сигналов Z1 и Z0 и сигналов на информационных входах триггеров Т1 и Т0.
Слайд 26
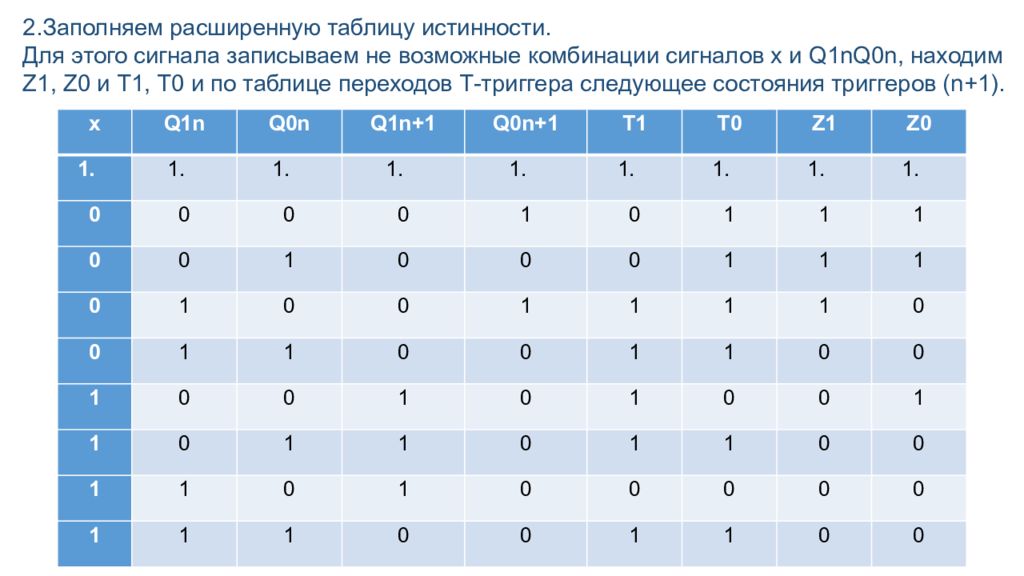
2.Заполняем расширенную таблицу истинности. Для этого сигнала записываем не возможные комбинации сигналов х и Q1nQ0n, находим Z1, Z0 и Т1, Т0 и по таблице переходов Т-триггера следующее состояния триггеров (n+1). х Q1n Q0n Q1n+1 Q0n+1 T1 T0 Z1 Z0 0 0 0 0 1 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 1 0 0 1 1 0 1 1 0 1 1 0 0 1 1 0 1 0 0 0 0 0 1 1 1 0 0 1 1 0 0
Слайд 28
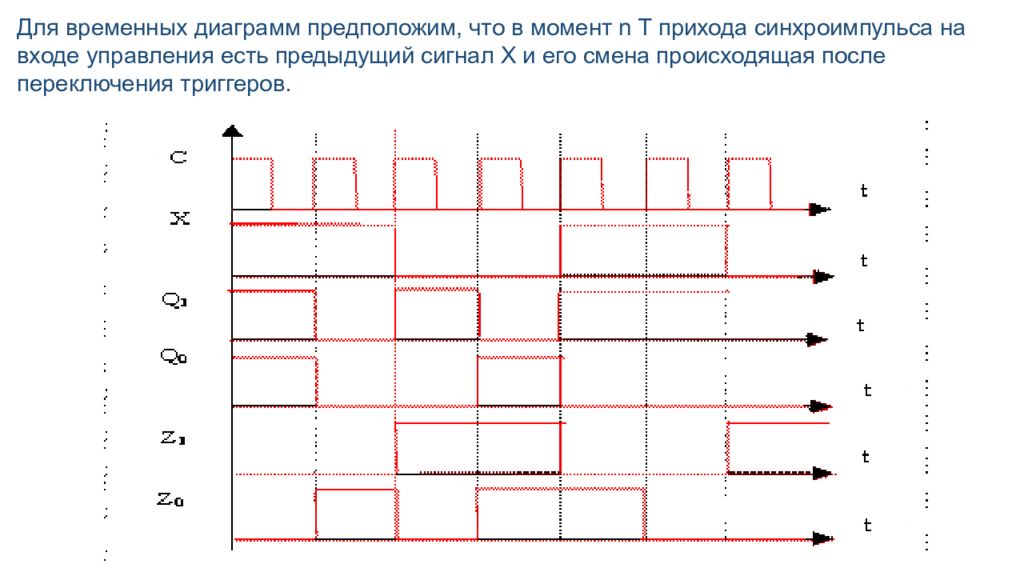
Для временных диаграмм предположим, что в момент n T прихода синхроимпульса на входе управления есть предыдущий сигнал Х и его смена происходящая после переключения триггеров.
Слайд 29
Понятие о комбинационной схеме и цифровом автомате При проектировании ЭВМ и ВС (вычислительных систем) значительное внимание уделяется выбору операционных блоков АЛУ (арифметико-логическое устройство - выполняет некоторый набор арифметических и логических операций над входными словами (операндами) фиксированной разрядности, выдавая результат в виде выходного слова той же разрядности) для реализации заданных логических и арифметических операций. Преобразование информации в ЭВМ производятся электронными схемами двух типов : комбинационными схемами цифровыми автоматами (накапливающимися или последовательными схемами). В комбинационных схемах ( КС ) результат преобразования (выходные сигналы) зависит только от комбинации сигналов, поданных на ее входы в данный момент времени. В КС отсутствуют элементы памяти, так что сигналы, действующие на входах КС, не сохраняются. Поэтому КС называют автоматами без памяти или примитивными автоматами, используемыми в основном для построения простейших узлов и функциональных блоков ЭВМ (шифраторов, дешифраторов, сумматоров, преобразователей кодов, схем контроля и др.).
Слайд 30
В цифровых автоматах ( ЦА ) в отличие от КС результат преобразования информации зависит не только от значений сигналов, поданных на входы в данный момент времени, но и от последовательности предыдущих состояний входов и выходов, т. е. внутренних состояний схемы. Для фиксации внутренних состояний ЦА должен содержать элементы памяти. Поэтому под ЦА понимают комбинационное устройство с памятью, называемое автоматом с памятью или полным автоматом. Они используются для построения триггерных устройств регистров, счетчиков, распределителей импульсов и др. По зависимости выходного сигнала от входного все электронные схемы разделяют на автоматы: Мили Мура. Мили и Мур исследовали их первыми. К автоматам Мили относятся комбинационные схемы, к автоматам Мура — цифровые автоматы. Переход от условий работы автомата к его функционированию осуществляется с помощью аппарата логики, или булевой алгебры, являющейся одной из ветвей математической логики.
Слайд 43
https://youtu.be/0L0catcHqy8?si=JgRTQbGatqwJfHsb https://youtu.be/0L0catcHqy8?si=JgRTQbGatqwJfHsb https://youtu.be/t0y7Tw7Nzh0?si=Fxl27QwVj4UVCAWy https:// youtu.be/EwmwzfS-uqU?si=WxfPwbRlZZsY7oYv https://youtu.be/T48GampeJ7c?si=IIFt04-5WyOs9TMg – конечный автомат https://youtu.be/qKKlm-BFJEM?si=O53kPmUpAX11WGpg – автомат Мили https://youtu.be/aqFQ_iMNWgY?si=Sj3n3wXyb4qdURrG – автомат мура
Слайд 44
В электронике, да и в программировании, в простейшем случае мы имеем дело с так называемыми «переключательными функциями». Это относительно примитивная абстракция не имеющая собственной памяти: мы на вход схемы аргумент, она на выход некое значение. Выходное значение всегда зависит только от входного. А если нам необходимо, чтобы последующее значение функции зависело от предыдущего? От нескольких предыдущих? Тут мы уже приходим к некой абстракции с собственной памятью. Это и будет автомат. Выходное значение на автомате зависит от значения на входе и текущего состояния автомата. Конечный автомат соответственно потому так называется, что число его внутренних состояний конечно. Наверное, самым простейшим из конечных автоматов является детерминированный: для каждого входного сигнала существует лишь одно состояние, в которое автомат может перейти из текущего.
Слайд 45
Таким образом, наш автомат определяется следующим: начальным состоянием; входным алфавитом (набором возможных входных сигналов); множеством состояний; таблицей переходов. Собственно, вся суть автомата определяется последним пунктом. Таблица переходов (также изображается как диаграмма переходов) состоит из 3-х столбцов: входной сигнал (символ), текущее состояние, следующее состояние. Конечный автомат можно представить в виде графа, вершины которого являются состояниями, а ребра — переходы между ними. Каждое ребро имеет метку, информирующую о том, когда должен произойти переход.
Слайд 46
Планирование состояний и их переходов Реализация конечного автомата начинается с выявления его состояний и переходов между ними. Представьте себе конечный автомат, описывающий действия муравья, несущего листья в муравейник: Отправной точкой является состояние « find leaf », которое остается активным до тех пор, пока муравей не найдет лист. Когда это произойдет, то состояние сменится на « go home ». Это же состояние останется активным, пока наш муравей не доберется до муравейника. После этого состояние вновь меняется на « find leaf ». Если состояние « find leaf » активно, но курсор мыши находится рядом с муравьем, то состояние меняется на « run away ». Как только муравей будет в достаточно безопасном расстоянии от курсора мыши, состояние вновь сменится на « find leaf ». Обратите внимание на то, что при направлении домой или из дома муравей не будет бояться курсора мыши. Почему? А потому что нет соответствующего перехода.