Задание 5
Система Счисления(СС ) -это способ записи числа с помощью символов. Основные системы счисления: Двоичная – состоит только из 0, 1 Восьмеричная - состоит из чисел от 0 до 7 Десятичная - состоит из чисел от 0 до 9 Шестнадцатеричная - состоит из чисел от 0 до 15. Причём начиная с 10 числа обозначаются буквами: А-10, B – 11, C – 12, D – 13, E – 14, F – 15.
Для перевода в некоторые системы счисления в python уже есть готовые функции, которые можно сразу вызывать. В ним относятся: bin(n) – перевод числа n из десятичной системы счисления в двоичную. Результат функции записывается в строковом типе данных oct (n) - перевод числа n из десятичной системы счисления в восьмеричную. Результат функции записывается в строковом типе данных int (‘n’, x) – перевод числа n из любой системы счисления в десятичную, где x – система счисления из которой переводят. n должно быть строкой. hex(n) - перевод числа n из десятичной системы счисления в шестнадцатеричная. Результат функции записывается в строковом типе данных
print(bin(879)) -> 0b1101101111 print( oct (879)) -> 0o1557 print( int ('872', 9)) -> 713 print(hex(879)) -> 0x36f Как работают встроенные функции Заметим, что при переводе числа в двоичную, восьмеричную или шестнадцатеричную систему счисления программа добавляет два символа, указывающие используемую систему. Для дальнейшей обработки данные символы не понадобятся, поэтому с помощью среза уберём их: print(bin(879)[2:]) - > 1101101111 print( oct (879)[2:]) -> 1557 print(hex(879)[2:])) -> 36f [2:] – означает, что мы берем срез строки, начиная с третьего символа (индекс 2) и до конца.
Если в задаче требуется перевести в СС отличную от 2-ой, 8-ой, 16-ой, то необходимо написать свой алгоритм перевода. Задание: перевести 45 из десятичной системы счисления в шестеричную. Напишем для этого функцию:
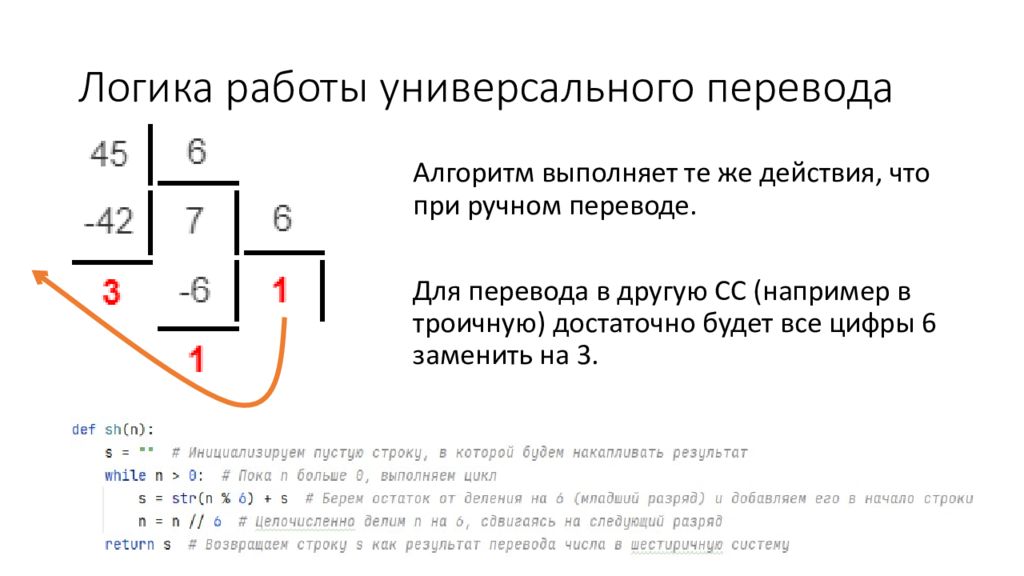
Алгоритм выполняет те же действия, что при ручном переводе. Для перевода в другую СС (например в троичную) достаточно будет все цифры 6 заменить на 3.
Бит чётности - это дополнительный контрольный бит, который добавляется к двоичному коду так, чтобы количество единиц в полученном двоичном коде стало чётным. Если в исходном коде уже было чётное количество единиц, дописывается 0, если нечётное — дописывается 1. Количество единиц можно проверить с помощью метода count: a = 1135 b = bin(a)[2:] if b.count ("1") % 2 == 0: print(True) else: print(False)
a = [] for n in range(1, 12): r = bin(n)[2:] if n % 2 == 0: r = '10' + r else: r = '1' + r + '01' a.append(int(r, 2)) print(min(a)) Будем перебирать n диапазоне чисел. Внутри этого цикла перепишем весь алгоритм из задачи на python. Создадим список a, в котором будем хранить все найденные, подходящие под условия задачи, числа. Необходимо вывести наименьшее число R, значит, воспользуемся функцией min.
a = [] for n in range(1, 10000): r = bin(n)[2:] if n % 3 == 0: r = r + r[-2] + r[-1] else: r = r + bin(n % 3 * 3)[2:] r = int(r, 2) if r >= 195: a.append(r) print(min(a)) Для вычисления двух последних чисел в записи воспользуемся индексами. У каждого элемента строки есть свой индекс начиная с 0, если смотреть слева-направо, или начиная с -1, начиная с справа-налево.
Необходимая СС отсутствует в функциях python, тогда напишем свою, воспользовавшись универсальным алгоритмом.
В троичной системе счисления используются только цифры 0, 1, 2. С помощью метода count можно посчитать количество каждой цифры, а затем их сложить. Однако нам нужна не сумма количеств цифр, а сумма самих цифр. Для этого умножим каждое найденное количество на соответствующую цифру и сложим результаты.
Сказано что число четырёхзначное, значит, будем перебирать от 1000 до 9999. Чтобы вычислить произведение цифр в числе, сначала переведём его в строковый тип данных. Это позволит обращаться к каждой цифре по индексу. Чтобы определить два наибольших произведения, воспользуемся сортировкой. Наибольшее произведение окажется на позиции -1 позиции,, а второе по величине — на -2.
Вспомним что такое бит чётности и как его проверять
Чтобы перевернуть число воспользуемся срезом. [::-1] означает срез с шагом -1 или в обратном порядке.
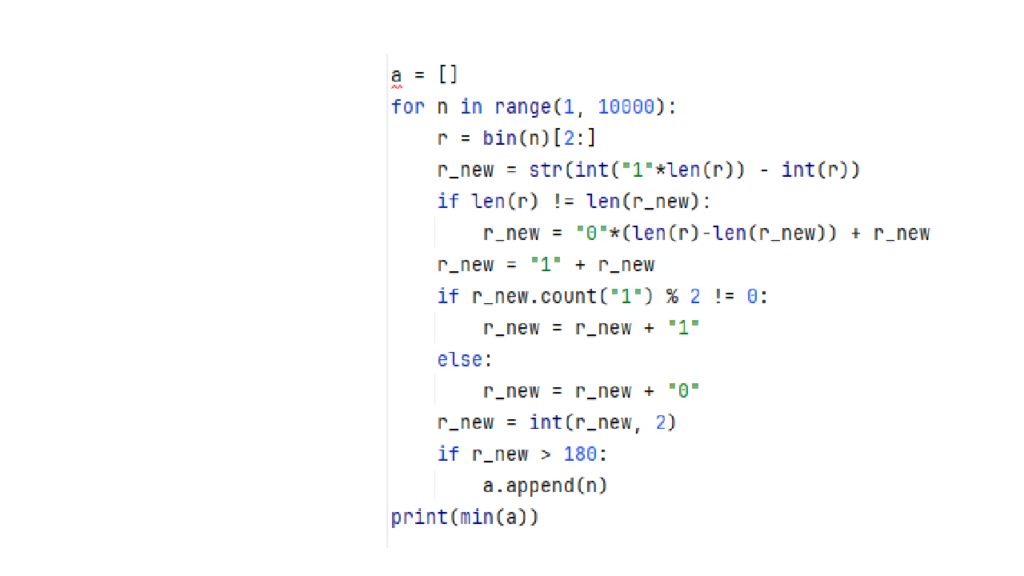
Для того чтобы производить замену, воспользуемся побитовой инверсией путём вычитания из числа, состоящего из всех единиц наше число. Пример 1 1 1 1 0 1 0 1 1 0 1 0 При переводе между разными типами данных незначащие нули (нули в начале числа, которые не изменяют его значение) должны сохраняться. После инвертирования число не должно сокращаться в длине. Если длина изменилась, необходимо добавить в начало инвертированного числа столько незначащих нулей, чтобы восстановить исходную длину: if len (r) != len ( r_new ): r_new = "0"*( len (r)- len ( r_new )) + r_new
Решить с сайта https://kompege.ru/course из 17 раздела (5 задание из ЕГЭ) номера 1-12 и 14 – 16
