Первый слайд презентации: Алгоритмизация и программирование. Язык Python
§ 41. Стек, дек, очередь 1
Слайд 2: Что такое стек?
2 Стек (англ. stack – стопка) – это линейный список, в котором элементы добавляются и удаляются только с одного конца («последним пришел – первым ушел»). LIFO = Last In – First Out. Системный стек: адреса возврата из подпрограмм передача аргументов подпрограмм хранение локальных переменных
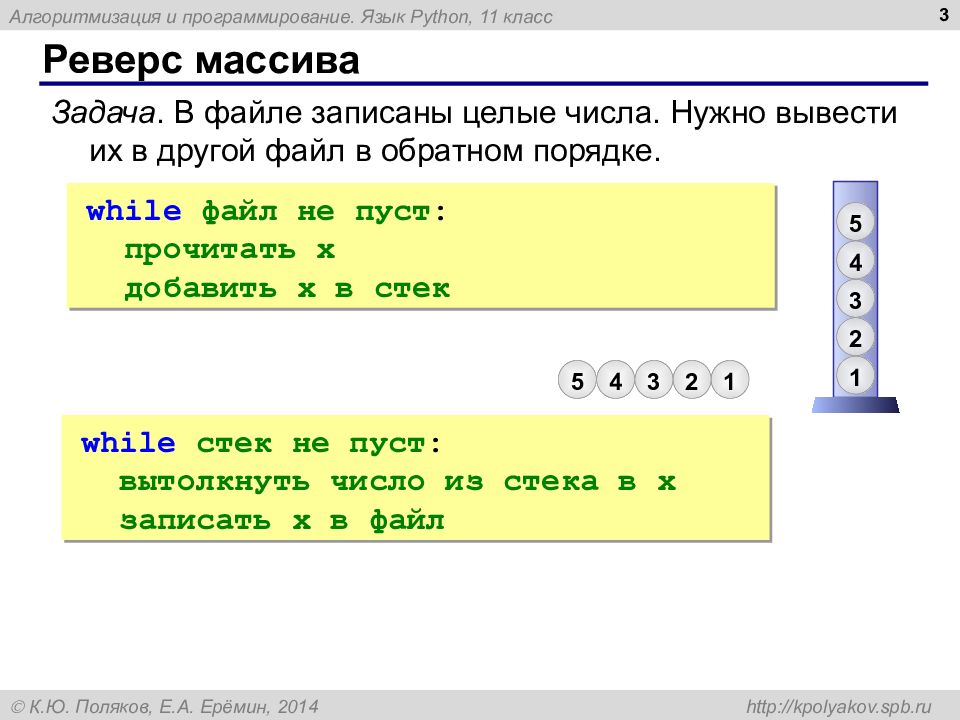
Слайд 3: Реверс массива
3 Задача. В файле записаны целые числа. Нужно вывести их в другой файл в обратном порядке. while файл не пуст : прочитать x добавить x в стек while стек не пуст : вытолкнуть число из стека в x записать x в файл 1 2 3 4 5 5 4 3 2 1
Слайд 4: Использование списка
4 stack = [] Создать стек: Конец списка – вершина стека! ! stack. append ( x ) «Втолкнуть» x в стек: x = stack. pop () Снять элемент с вершины стек в x : удалить последний элемент вернуть удалённый элемент как результат функции
Слайд 5: Инверсия массива неизвестной длины
5 F = open ( "input.txt" ) stack = [] while True : s = F. readline () if not s: break stack. append ( int (s) ) F. close () Чтение из файла: stack = [] for s in open ( "input_arr.dat" ): stack. append ( int ( s ) ) или так:
Слайд 6: Инверсия массива неизвестной длины
6 F = open ( "output.txt", "w" ) while len (stack) > 0 : x = stack. pop () F. write ( str (x) + "\n" ) F. close () Запись в файл (в обратном порядке):
Слайд 7: Вычисление арифметических выражений
7 Как компьютер вычисляет арифметические выражения ? ? (5+15)/(4+7-1) инфиксная форма (знак операции между данными) первой стоит последняя операция (вычисляем с конца) 1920 ( Я. Лукашевич ) : префиксная форма (знак операции перед данными) / + 5 15 - + 4 7 1 / 20 - + 4 7 1 / 20 - 11 1 / 20 1 0 2 не нужны скобки
Слайд 8: Вычисление арифметических выражений
8 (5+15)/(4+7-1) 1950-е : постфиксная форма (знак операции после данных) не нужны скобки вычисляем с начала 5 15 + 4 7 + 1 - / 20 4 7 + 1 - / 20 11 1 - / 20 1 0 / 2 Вычисляем с помощью стека! !
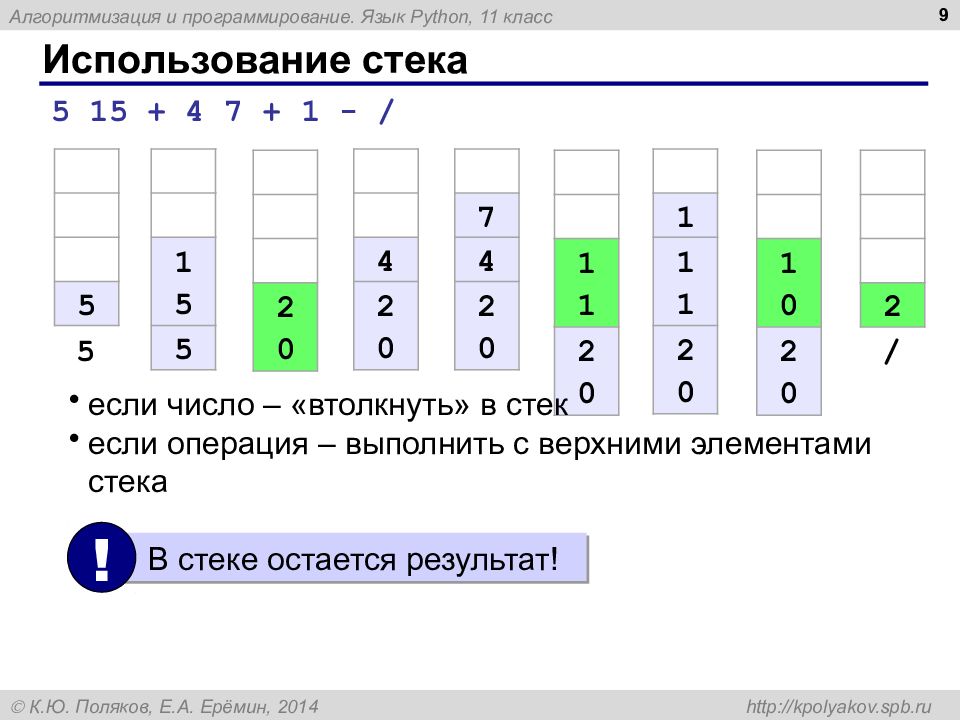
Слайд 9: Использование стека
9 5 5 15 + 4 7 + 1 - / 15 5 20 4 20 7 4 20 11 20 1 11 20 10 20 2 В стеке остается результат! ! 5 15 + 4 7 + 1 - / если число – «втолкнуть» в стек если операция – выполнить с верхними элементами стека
Слайд 10: Вычисление постфиксной формы
10 data = input (). split () stack = [] for x in data: if x in "+-*/" : # если операция op2 = int (stack. pop ()) op1 = int (stack. pop ()) if x == "+" : res = op1 + op2 elif x == "-" : res = op1 - op2 elif x == "*" : res = op1 * op2 else : res = op1 // op2 stack. append ( res ) else : stack. append ( x ) print ( stack[0] ) # результат разбить строку на элементы взять 2 значения со стека выполнить операцию результат в стек данные в стек
Слайд 11: Скобочные выражения
11 Задача. Вводится символьная строка, в которой записано некоторое (арифметическое) выражение, использующее скобки трёх типов: ( ), [ ] и { }. Проверить, правильное ли расставлены скобки. ()[{()[]}] [() )( [()} ([)] Для одного типа скобок: ( ) ( ( ) ( ( ) ) ) счётчик 0 1 0 1 2 1 2 3 2 1 0 Когда выражение правильное? ? счётчик всегда 0 в конце счётчик = 0 ( { [ ) } ] Для разных скобок не работает! !
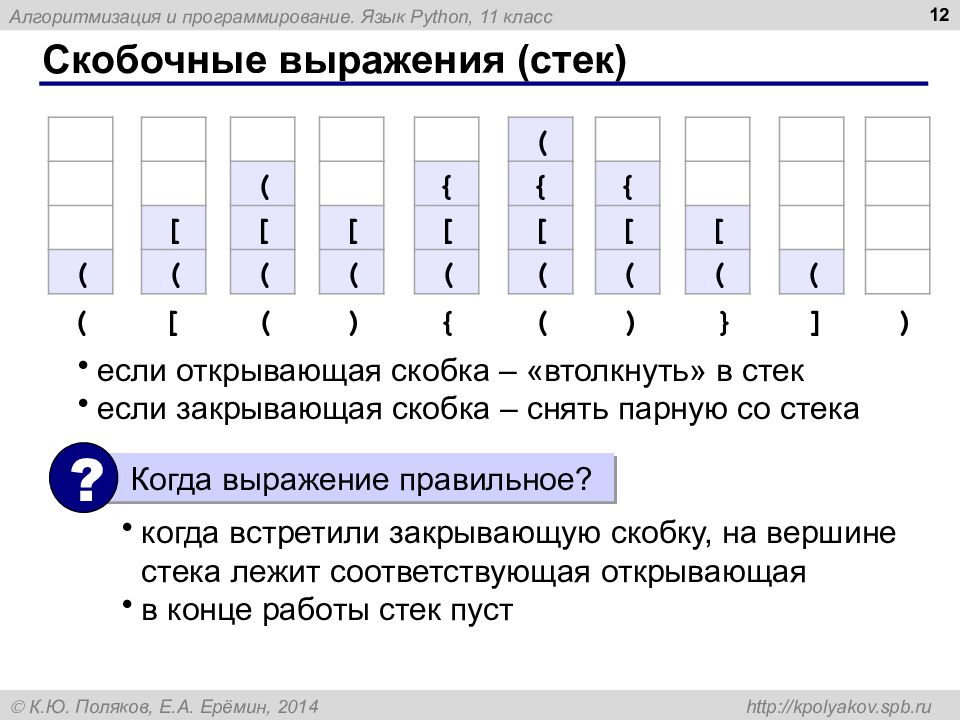
Слайд 12: Скобочные выражения (стек)
12 ( [ ( ) { ( ) } ] ) ( [ ( ( [ ( [ ( { [ ( ( { [ ( { [ ( [ ( ( Когда выражение правильное? ? когда встретили закрывающую скобку, на вершине стека лежит соответствующая открывающая в конце работы стек пуст если открывающая скобка – «втолкнуть» в стек если закрывающая скобка – снять парную со стека
Слайд 13: Скобочные выражения (стек)
13 L = "([{" # открывающие скобки R = ")]}" # парные закрывающие stack = [] # пустой стек err = False # признак ошибки Подготовка: Вывод результата: if not err : print ( "Выражение правильное." ) else : print ( "Выражение неправильное." )
Последний слайд презентации: Алгоритмизация и программирование. Язык Python: Скобочные выражения (стек)
14 for c in s: p = L. find (c) if p >= 0: stack. append (c) p = R. find (c) if p >= 0: if len(stack) == 0: err = True else : top = stack. pop () if p!= L. find (top): err = True if err : break открывающую скобку в стек если закрывающая скобка… если не та скобка… Что ещё? ?