Слайд 2
Четырехугольник — фигура, состоящая из четырех точек и четырех отрезков, последовательно их соединяющих; причем ни одна из четырех данных точек не лежит на одной прямой, а отрезки, соединяющие их, не пересекаются.
Слайд 3
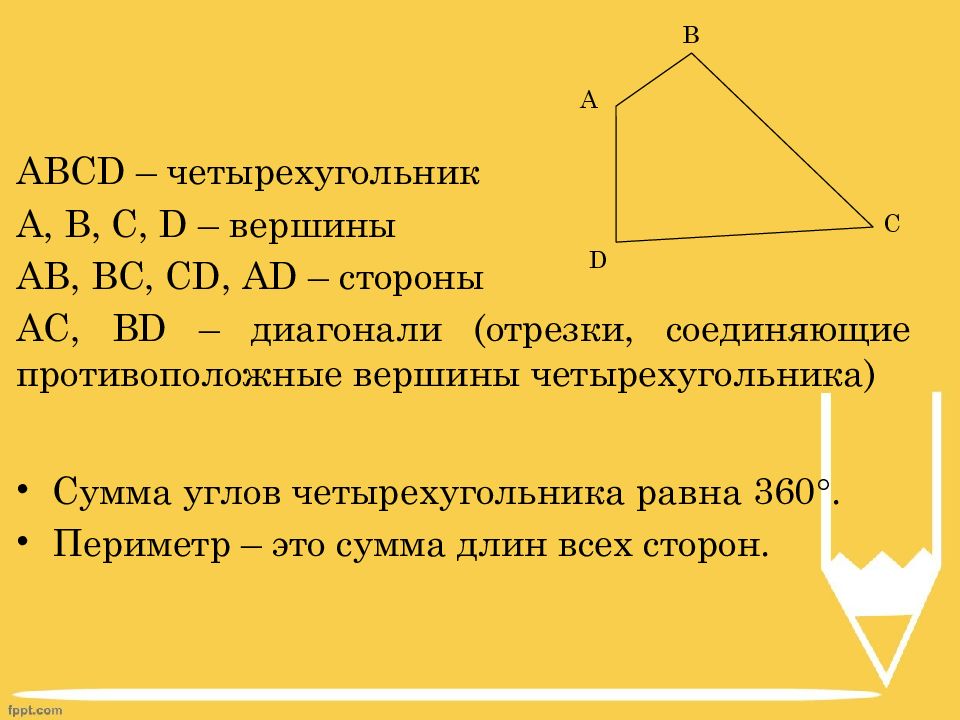
ABCD – четырехугольник A, B, C, D – вершины AB, BC, CD, AD – стороны AC, BD – диагонали (отрезки, соединяющие противоположные вершины четырехугольника) A B C D Сумма углов четырехугольника равна 360 . Периметр – это сумма длин всех сторон.
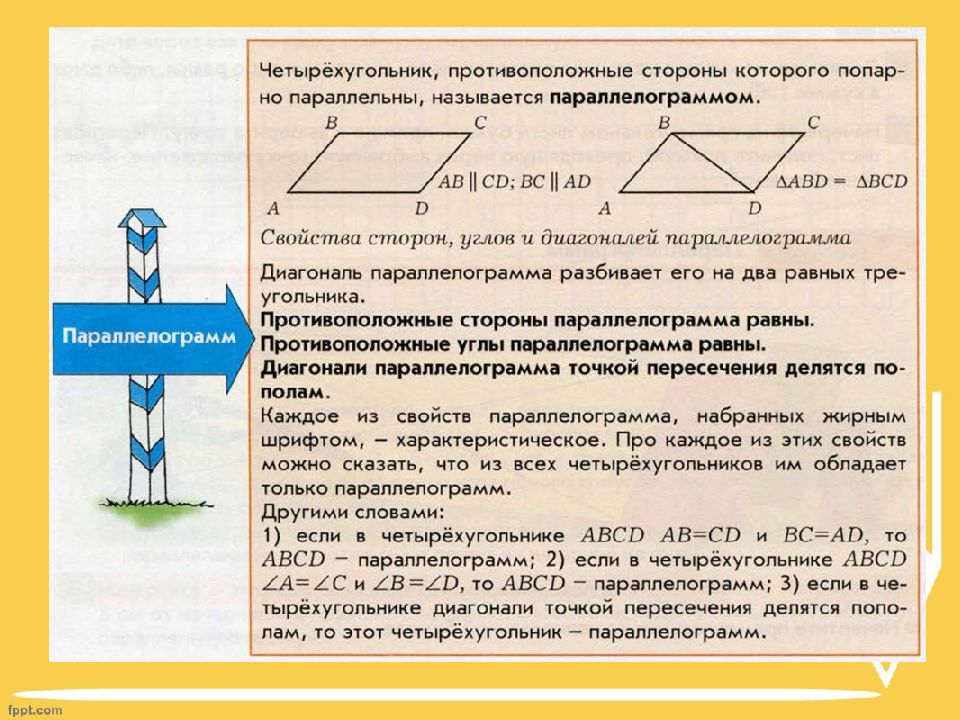
Слайд 4: Параллелограмм
Это четырехугольник, у которого стороны попарно параллельны ( AB CD, BC AD). Свойство первое: углы, прилежащие к одной стороне составляют в сумме 180. Свойство второе: в параллелограмме противоположные стороны и противоположные углы равны. Свойство третье: диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. P = AB + BC + CD + AD = 2(AB + BC) A D C B
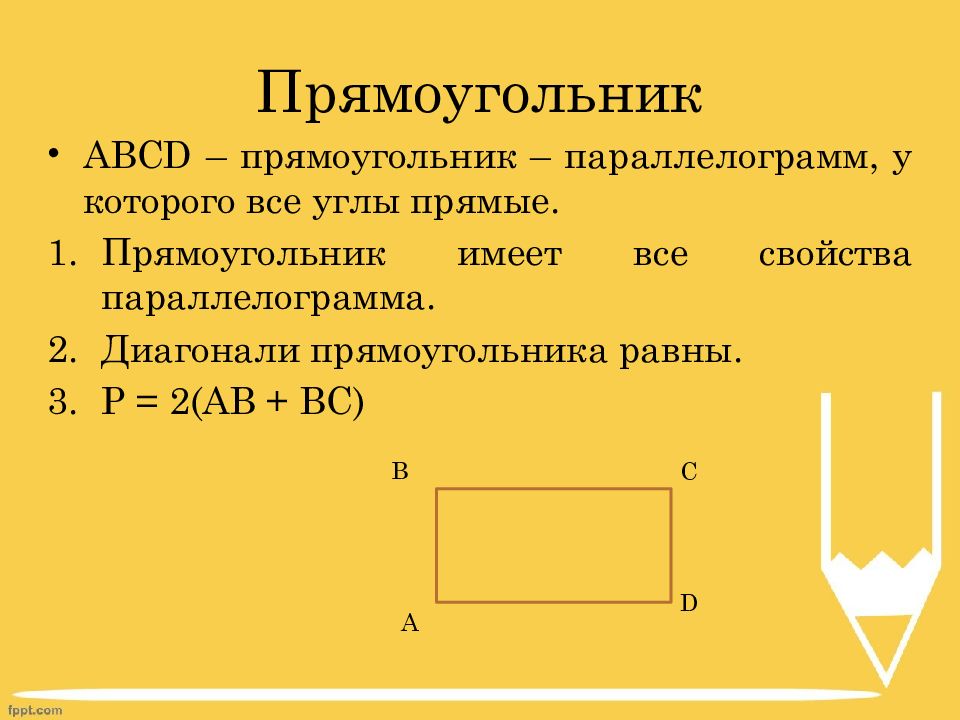
Слайд 7: Прямоугольник
ABCD – прямоугольник – параллелограмм, у которого все углы прямые. Прямоугольник имеет все свойства параллелограмма. Диагонали прямоугольника равны. P = 2(AB + BC) A D C B
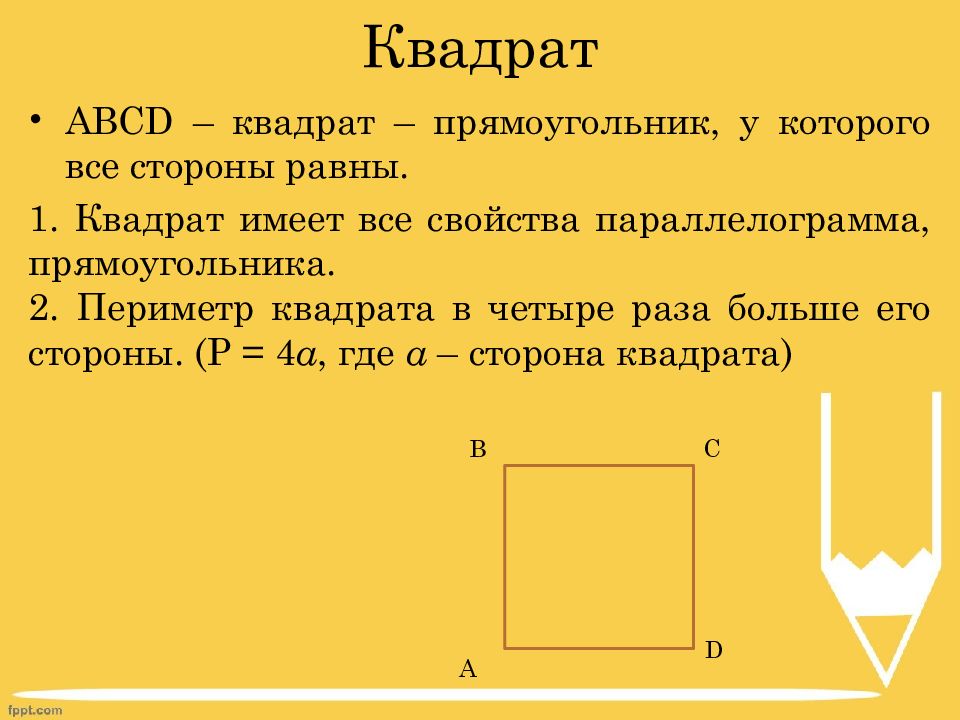
Слайд 8: Квадрат
ABCD – квадрат – прямоугольник, у которого все стороны равны. 1. Квадрат имеет все свойства параллелограмма, прямоугольника. 2. Периметр квадрата в четыре раза больше его стороны. ( P = 4 a, где a – сторона квадрата) A D C B
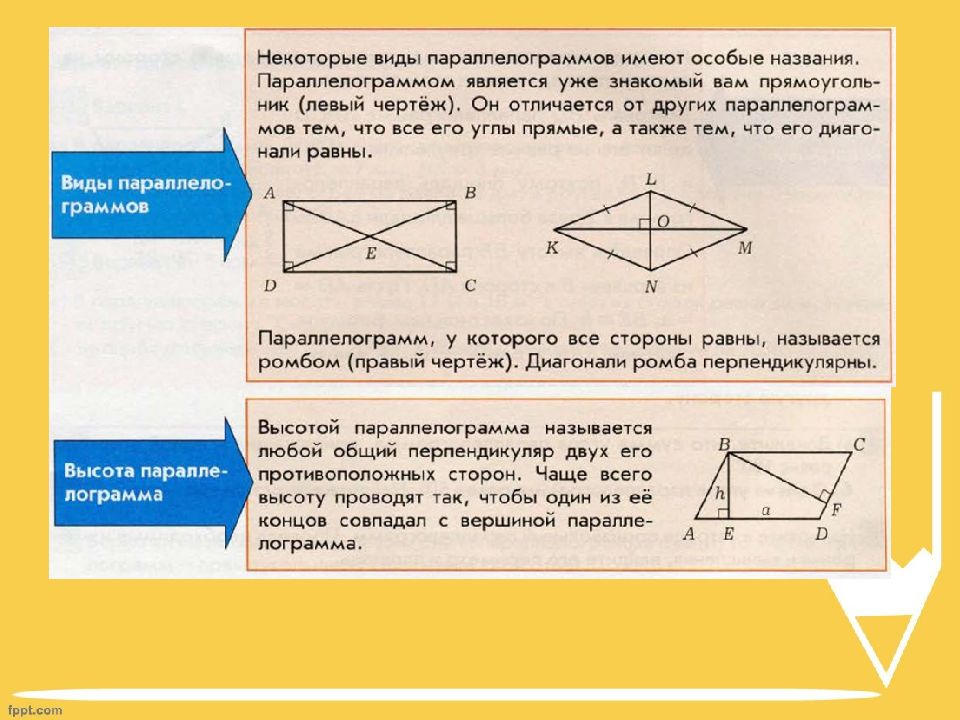
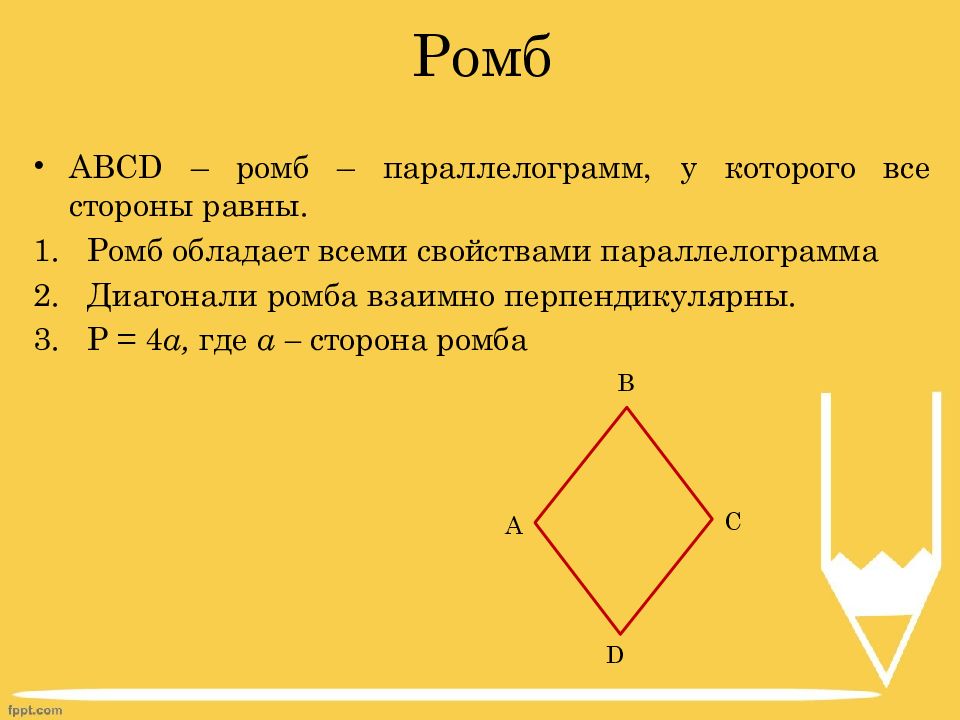
Слайд 9: Ромб
ABCD – ромб – параллелограмм, у которого все стороны равны. Ромб обладает всеми свойствами параллелограмма Диагонали ромба взаимно перпендикулярны. P = 4 a, где a – сторона ромба A B C D
Слайд 10
Четырехугольник Формула периметра Параллелограмм P = 2( a+b ) Прямоугольник P = 2( a+b ) Ромб P = 4a Квадрат P = 4a
Слайд 11
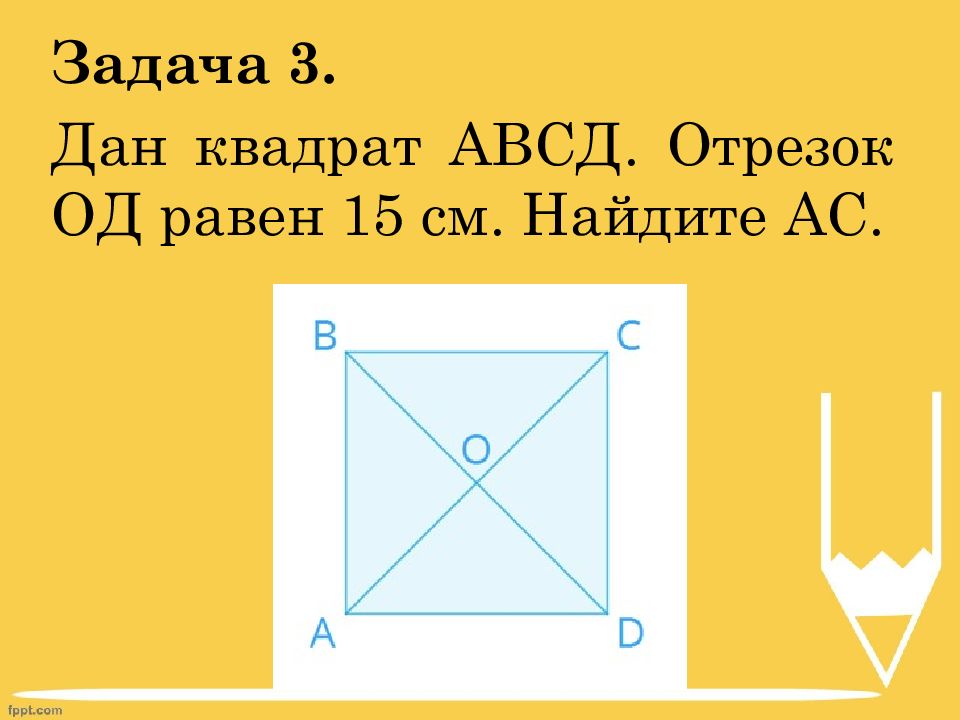
Задача 1. Одна сторона прямоугольника равна 25 см, другая – на 8 см меньше. Вычислите периметр прямоугольника.