Слайд 2: Повторение
Что такое комбинаторика? Что такое перебор ? Расскажите правило умножения Что такое перестановки? Что такое факториал? Что такое размещения? https://t.me/zanimmath
Слайд 3: Задача 1
Из класса, в котором учится 25 человек, нужно выбрать двоих для участия в олимпиаде по краеведению. Сколькими способами это можно сделать? https://t.me/zanimmath
Слайд 4: Задача 1
Из класса, в котором учится 25 человек, нужно выбрать двоих для участия в олимпиаде по краеведению. Сколькими способами это можно сделать ? Решение: первого ученика можно выбрать 25 способами, после чего второго — 24 способами. Всего таких способов по правилу умножения будет 25 ∙ 24 = 600. Однако при выборе пары учеников для участия в олимпиаде их порядок в паре не имеет значения. Получается, что каждую пару мы посчитали дважды, поэтому правильным ответом будет (25 ∙ 24):2 = 300 Ответ: 300 https://t.me/zanimmath
Слайд 5: Задача 2
Из 11 футболистов, участвовавших в матче, нужно выбрать троих для проведения антидопинговой пробы. Сколькими способами это можно сделать ? https://t.me/zanimmath
Слайд 6: Задача 2
Из 11 футболистов, участвовавших в матче, нужно выбрать троих для проведения антидопинговой пробы. Сколькими способами это можно сделать? Решение: первого игрока можно выбрать 11 способами, после чего второго — 10 и третьего — 9 способами. Всего таких способов будет 11 ∙ 10 ∙ 9 = 990. Однако при выборе тройки футболистов порядок их выбора не имеет значения. Посмотрим, сколько же раз мы посчитали каждую тройку. Для этого нужно найти, сколькими способами можно упорядочить тройку футболистов, не меняя её состава. На первое место можно поставить любого из трёх выбранных футболистов, на второе — любого из двух, и для третьего места остаётся только один вариант. Значит, мы посчитали каждую тройку футболистов 3 ∙ 2 ∙ 1 = 6 раз. Поэтому правильным ответом в этой задаче будет (11 ∙ 10 ∙ 9):6=165 Ответ: 165 https://t.me/zanimmath
Слайд 7: Сочетания
В двух приведённых примерах мы столкнулись с комбинациями, в которых порядок элементов не учитывается. Такие комбинации называются сочетаниями. Сочетанием из N элементов по k называют комбинацию, составленную из любых k этих элементов без учёта их порядка. https://t.me/zanimmath
Слайд 8: Сочетания
Ранее мы с вами считали размещения. Формула для подсчёта сочетаний получена на основе формулы размещений: Количество сочетаний из N по k обозначается в комбинаторике обозначается буквой С, где буква C берётся от французского слова combination — « комбинация » https://t.me/zanimmath
Слайд 9: Задача 3
В текущем учебном году десятиклассникам предлагаются на выбор 7 дополнительных предметов, из которых они должны выбрать для посещения 4. Сколькими способами это можно сделать? https://t.me/zanimmath
Слайд 10: Задача 3
В текущем учебном году десятиклассникам предлагаются на выбор 7 дополнительных предметов, из которых они должны выбрать для посещения 4. Сколькими способами это можно сделать ? Решение: В этой ситуации нам нужно выбрать 4 предмета из 7, причём порядок выбора значения не имеет — важен только состав этой четвёрки. Значит, речь идёт о сочетаниях из 7 по 4. Находим их количество по формуле Ответ: 35 https://t.me/zanimmath
Слайд 12: Реши самостоятельно
Задача 1. Чему равны числа Задача 2. Чему равны числа Задача 3. Чему равна сумма чисел https://t.me/zanimmath
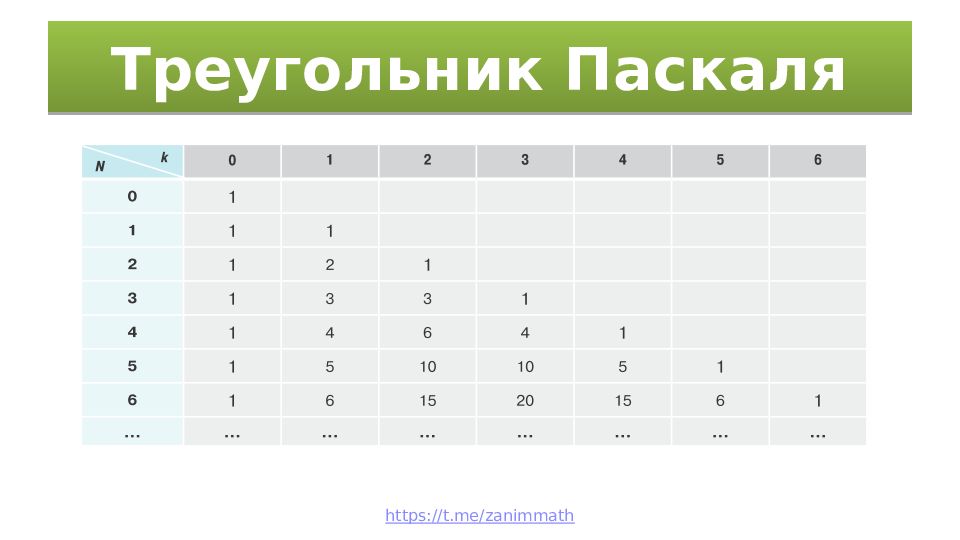
Слайд 13: Треугольник Паскаля
Свойство 5, позволяет находить сочетания из N по k вообще без использования факториалов. Для этого нужно последовательно применять полученную рекуррентную формулу при N = 1, 2, 3 и т. д. После чего мы можем получить такого рода таблицу: https://t.me/zanimmath
Слайд 15: Треугольник Паскаля
Полученная таблица, составленная из чисел, носит название треугольника Паскаля по имени замечательного французского учёного Блеза Паскаля (1623—1662). Первое упоминание этой конструкции из чисел встречается гораздо раньше в трудах древнеиндийских математиков, но Паскаль посвятил ей «Трактат об арифметическом треугольнике», в котором обнаружил ряд других замечательных закономерностей, помимо рекуррентного соотношения между строками треугольника. https://t.me/zanimmath
Слайд 16: Треугольник Паскаля
https://t.me/zanimmath Если сложить числа в любой строке, то по свойству 4 получится соответствующая степень двойки, например для седьмой строки ( треугольник начинается с нулевой строки! ): 1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128 То есть получили 7 степень двойки
Последний слайд презентации: Число сочетаний. Треугольник Паскаля: Задание на дом
Задача 1. Из класса, в котором учится 13 мальчиков и 17 девочек, нужно набрать команду для участия в школьной олимпиаде по спортивному многоборью. В команде должно быть 2 мальчика и 2 девочки. Сколькими способами это можно сделать? Задача 2. Для поездки на экскурсию 30 участников олимпиады нужно распределить по трём микроавтобусам, каждый из которых вмещает 10 человек. Сколькими способами это можно сделать? Задача 3. Запиши 10 строчку треугольника Паскаля. Сколько чисел в этой строке? https://t.me/zanimmath Ответы: Задача 1. 10608 Задача 2. 5 550 996 791 340 Задача 3. 11