Декартовы координаты в пространстве
Урок 1
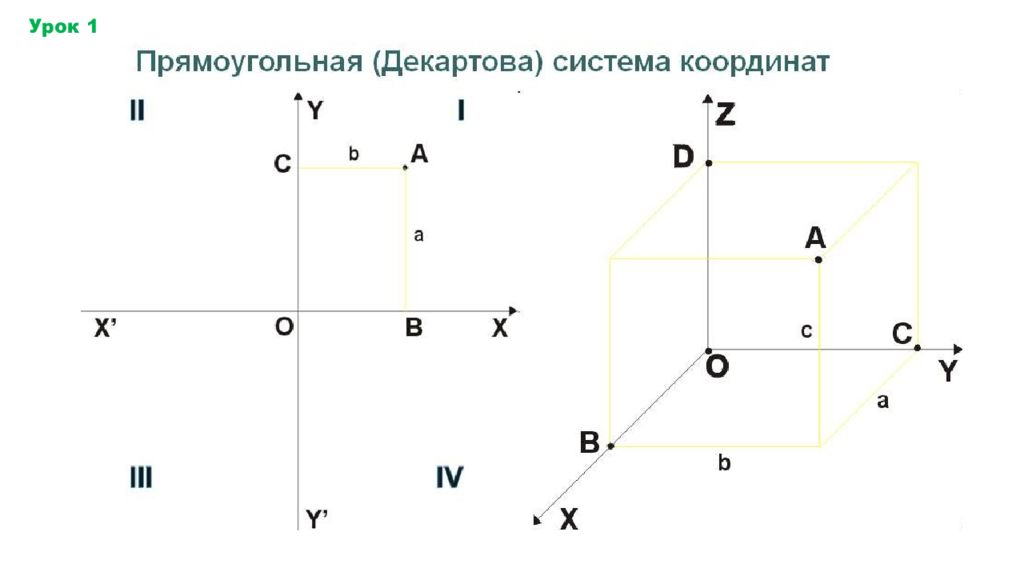
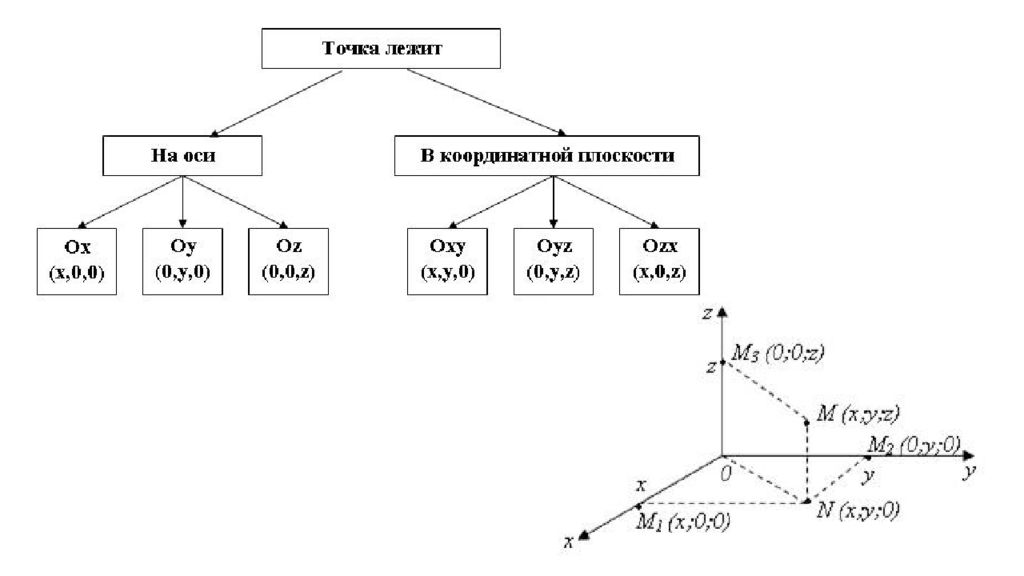
Координата x точки А – число, равное по абсолютной величине длине отрезка лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси. Координаты записываются А( x ; y ; z)
Задача:
Тема: « Расстояние между точками. Координаты середины отрезка» Цель урока: Закрепление знаний о координатах в пространстве; Изучение формул для вычисления расстояния между точками, координат середины отрезка; Применение формулы для решения задач.
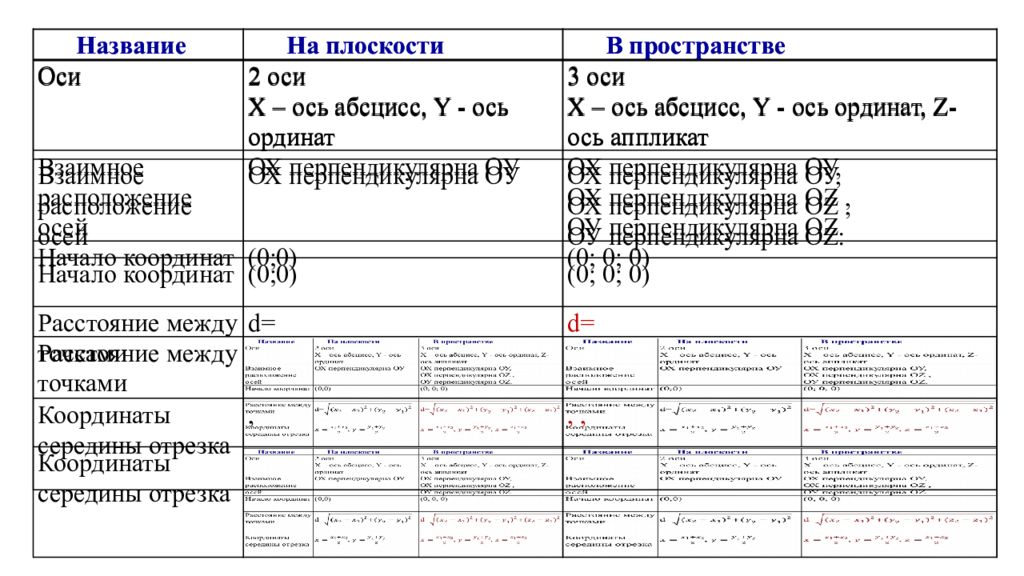
Название На плоскости В пространстве Оси 2 оси X – ось абсцисс, Y - ось ординат 3 оси X – ось абсцисс, Y - ось ординат, Z- ось аппликат Взаимное расположение осей ОХ перпендикулярна ОУ ОХ перпендикулярна ОУ, ОХ перпендикулярна ОZ, ОУ перпендикулярна ОZ. Начало координат (0;0) (0; 0; 0) Расстояние между точками d= d= Координаты середины отрезка , ,, Название На плоскости В пространстве Оси 2 оси X – ось абсцисс, Y - ось ординат 3 оси X – ось абсцисс, Y - ось ординат, Z- ось аппликат Взаимное расположение осей ОХ перпендикулярна ОУ ОХ перпендикулярна ОУ, ОХ перпендикулярна ОZ, ОУ перпендикулярна ОZ. Начало координат (0;0) (0; 0; 0) Расстояние между точками Координаты середины отрезка
Решим задачи: 1. Найдите расстояние между точками А и В, если А(9;3;-5) и В (2;10; -5). 2. Найдите координаты середины отрезка, соединяющего точки А (-2;4;0) и В (-4;10;6).
Задачи для самостоятельной работы: № 1.9 № 1.11 № 1.15
Домашнее задание: Параграф 1, ответы на вопросы, записи ТТ № 1.4, 1.6, 1.8, 1.12, 1.16
Повторение Проверочная работа 1.Напишите координаты точки, которая лежит: На оси X На оси Y На оси Z В плоскости XY В плоскости XYZ В плоскости YZ 2. В какой плоскости лежат точки? (0;5;6) (1;2;3) (1;0;3) (1;2;0) Урок 2
Ответы для взаимопроверки: 1. ( X ;0;0) ( 0 ; У ;0) ( 0 ; 0 ;Z) ( X ;У;0) (X; У; Z ) (0;Y;Z) 2. В какой плоскости лежат точки? YZ XYZ XZ XY
Критерии оценки: 10-9 – оценка «5» 8-7 – оценка «4» 6-5 – оценка «3» Менее 5 – оценка «2»
Решим задачи: № 1.9, 1.13, 1.17, 1.18, 1.20, 1.22, 1.24
Домашнее задание: № 1.14, 1.19, 1.21, 1.23, 1.25
