Слайд 2: Деревья решений
Дерево решений – это графическое представление процесса принятия решения, в котором отображаются возможные варианты решений, состояния природы, вероятности их наступления, а также платежи при различных сочетаниях состояний природы и возможных решениях (Мадера)
Слайд 3: Структура дерева решений
Дерево решений состоит из узлов и ветвей. Узлы бывают трех типов: Узел решений Узел событий Конечный узел. Ветви дерева решений подразделяются на Ветви решений Ветви событий Конечные ветви
Слайд 4: Структура дерева решений
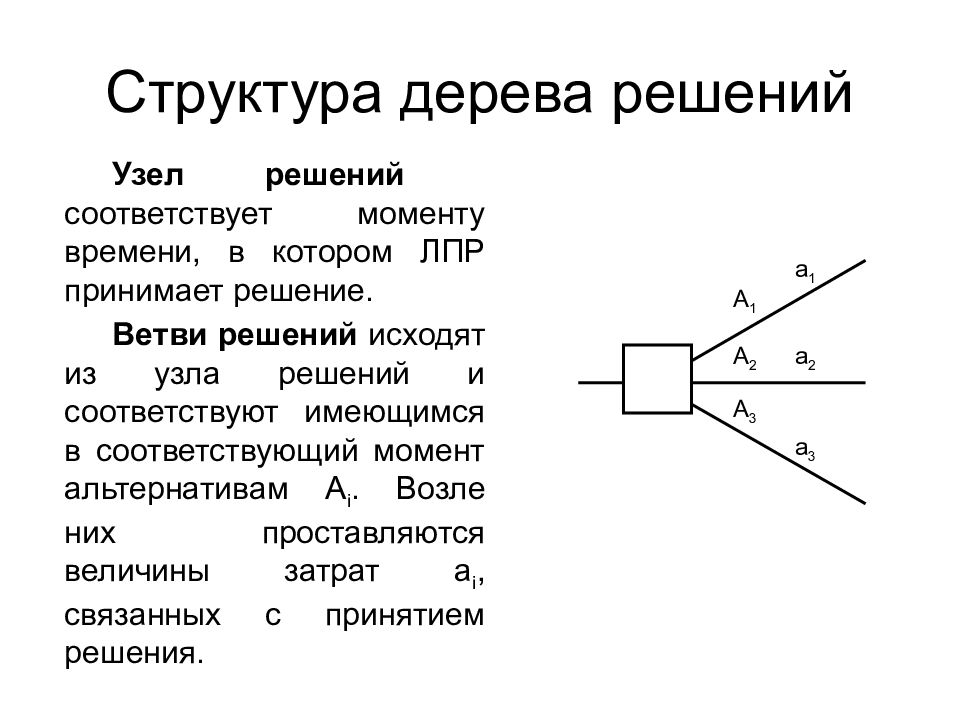
Узел решений соответствует моменту времени, в котором ЛПР принимает решение. Ветви решений исходят из узла решений и соответствуют имеющимся в соответствующий момент альтернативам A i. Возле них проставляются величины затрат a i, связанных с принятием решения. A 1 A 2 A 3 a 1 a 2 a 3
Слайд 5: Структура дерева решений
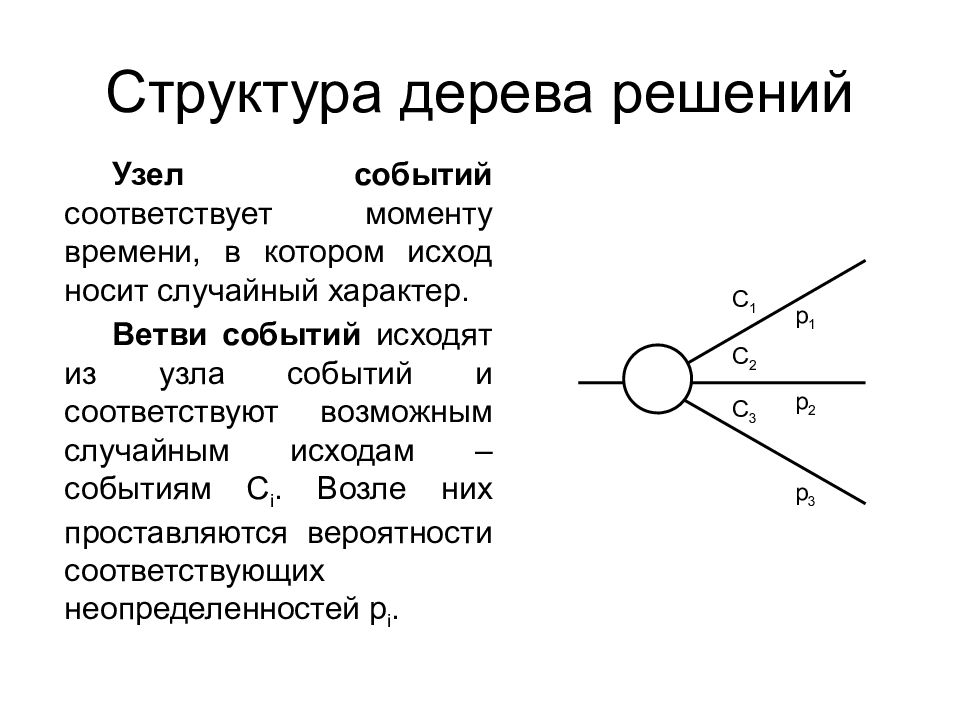
Узел c обытий соответствует моменту времени, в котором исход носит случайный характер. Ветви событий исходят из узла событий и соответствуют возможным случайным исходам – событиям C i. Возле них проставляются вероятности соответствующих неопределенностей p i. C 1 C 2 C 3 p 1 p 2 p 3
Слайд 6: Структура дерева решений
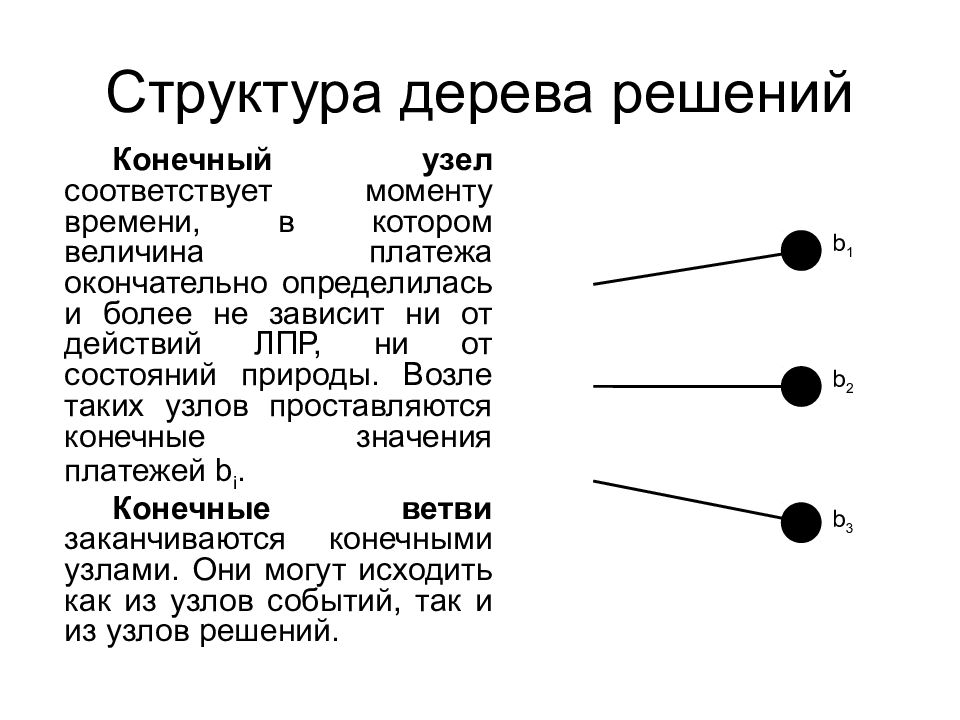
Конечный узел соответствует моменту времени, в котором величина платежа окончательно определилась и более не зависит ни от действий ЛПР, ни от состояний природы. Возле таких узлов проставляются конечные значения платежей b i. Конечные ветви заканчиваются конечными узлами. Они могут исходить как из узлов событий, так и из узлов решений. b 2 b 1 b 3
Слайд 7: Построение дерева решений
Дерево решений строится слева направо. Его структура отражает последовательность принятия решений в хронологическом порядке. Построение дерева начинается с узла, называемого корневым, и заканчивается конечными узлами.
Слайд 8: Виды деревьев решений
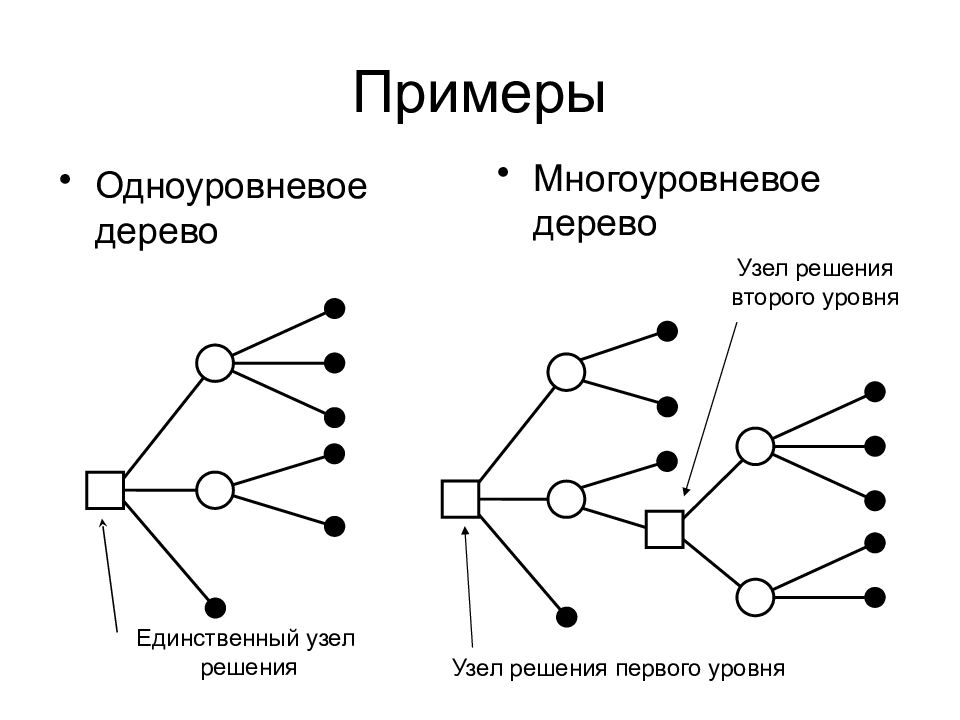
Одноуровневые деревья решений соответствуют ситуации, когда принимается одно решение из нескольких возможных альтернатив, причем результат зависит также от случайных исходов состояний природы. Часто такому дереву можно поставить в соответствие матрицу платежей, и наоборот, любой платежной матрице соответствует одноуровневое дерево решений. Многоуровневые деревья решений отражают принятие последовательных решений, когда решения предыдущего уровня порождают новые возможные решения и новые неопределенные исходы на следующем уровне.
Слайд 9: Примеры
Многоуровневое дерево Одноуровневое дерево Единственный узел решения Узел решения первого уровня Узел решения второго уровня
Слайд 10: Определение наилучшего решения
Наилучшее решение находят методом обратного пересчета. Метод основан на критерии максимального ожидаемого платежа. Обратный пересчет осуществляется при движении по дереву от конечных узлов к корневому. Вычисляются ожидаемые платежи для всех узлов решений и событий. Для узла решения в качестве ожидаемого платежа берется максимальное значение ожидаемого платежа в дочерних узлах (с учетом затрат). Для узла события ожидаемый платеж равен сумме произведений платежей в дочерних узлах на вероятности перехода в эти узлы.
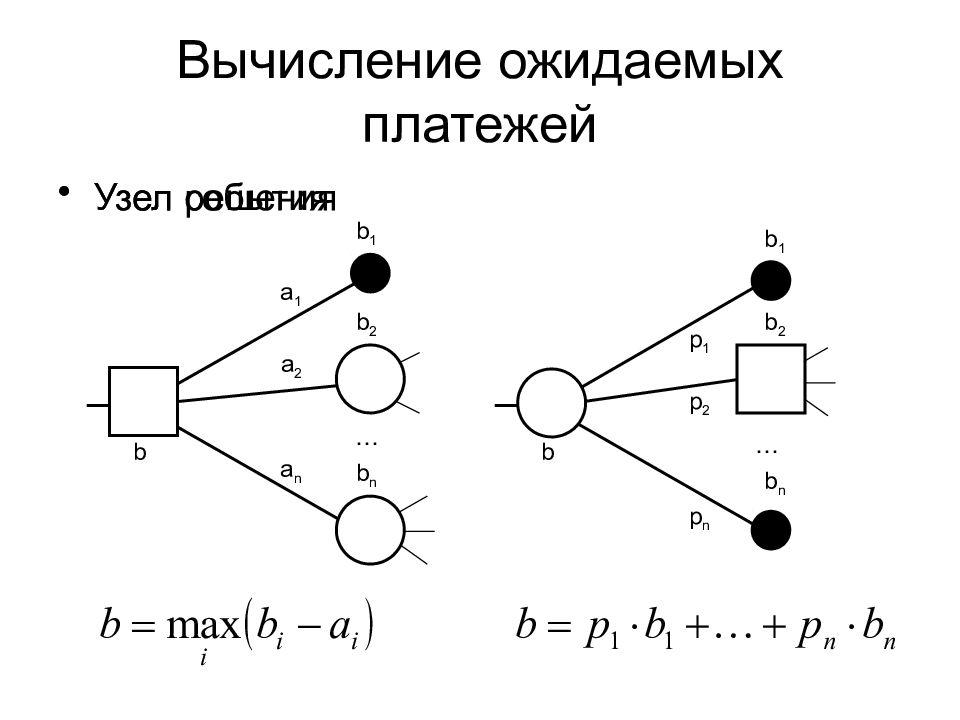
Слайд 11: Вычисление ожидаемых платежей
Узел решения Узел события a 1 a 2 a n p 1 p 2 p n b 1 b 2 b n b 1 b 2 b n b b … …
Слайд 12: Пример
Рассмотрим процесс построения и использования дерева решений на примере следующей задачи: Фирма закончила разработку технологии выпуска нового товара, и теперь её руководство должно принять решение о дальнейших действиях. Всего существует три возможности. Во-первых, фирма может создать крупное производство нового товара. Этот вариант приносит наибольшую прибыль в случае успеха, но требует значительных вложений: 180 д.е. Во-вторых, можно организовать малое предприятие, что потребует 80 д.е. В-третьих, фирма может продать технологию выпуска другому предприятию за 10 д.е.
Слайд 13: Пример
Прибыль, получаемая фирмой, зависит также от реакции рынка на новый товар. По мнению экспертов, вероятность благоприятной для фирмы ситуации на рынке составляет 0,4. Доходы фирмы в зависимости от выбранного варианта и состояния рынка представлены в таблице. Действие фирмы Реакция рынка Благо-приятная Неблаго- Приятная Крупное производство 400 д.е. 40 д.е. Малое производство 200 д.е. 20 д.е. Продажа патента 10 д.е.
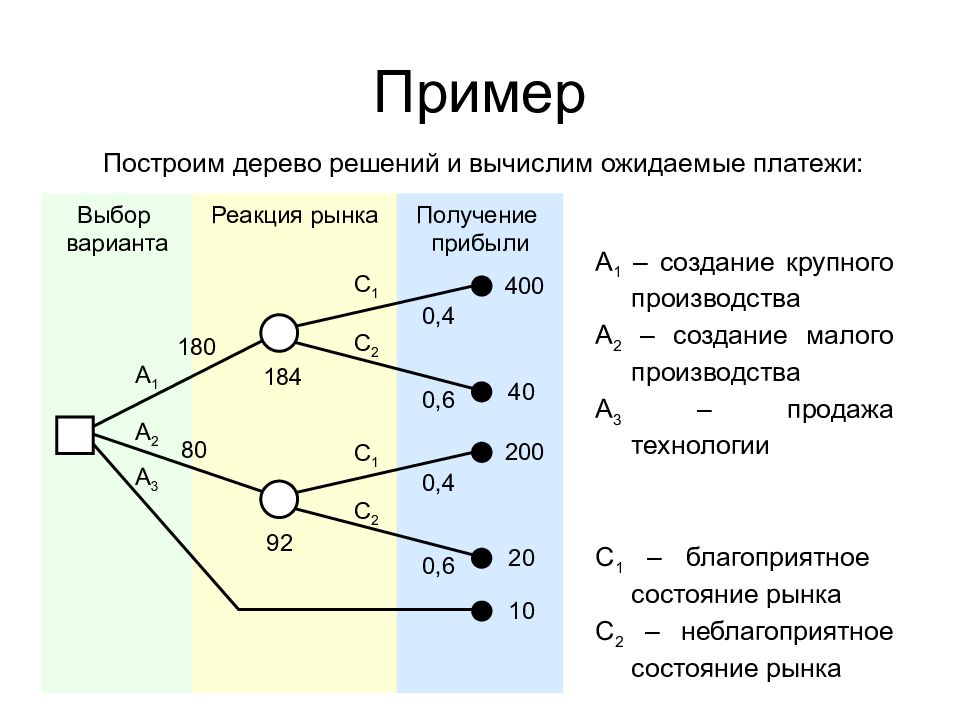
Слайд 14: Пример
Построим дерево решений и вычислим ожидаемые платежи: Реакция рынка Получение прибыли Выбор варианта 200 20 10 0,4 0,6 180 80 184 92 400 40 0,4 0,6 A 1 A 2 A 3 С 1 С 2 С 1 С 2 А 1 – создание крупного производства А 2 – создание малого производства А 3 – продажа технологии С 1 – благоприятное состояние рынка С 2 – неблагоприятное состояние рынка
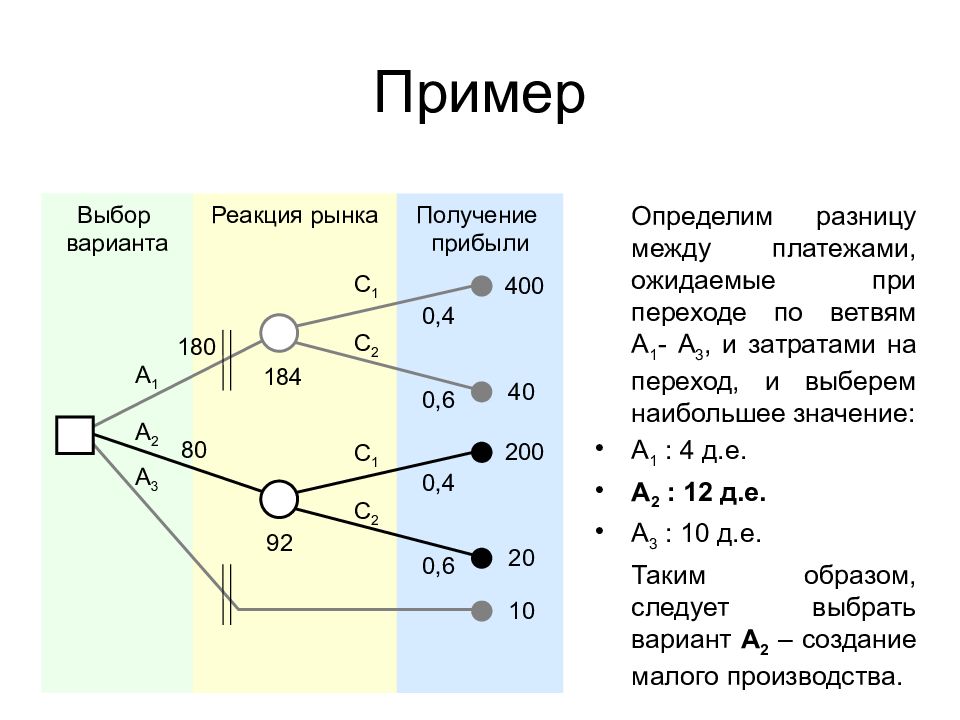
Слайд 15: Пример
Реакция рынка Получение прибыли Выбор варианта 200 20 10 0,4 0,6 180 80 184 92 400 40 0,4 0,6 A 1 A 2 A 3 С 1 С 2 С 1 С 2 Определим разницу между платежами, ожидаемые при переходе по ветвям А 1 - А 3, и затратами на переход, и выберем наибольшее значение: А 1 : 4 д.е. А 2 : 12 д.е. А 3 : 10 д.е. Таким образом, следует выбрать вариант А 2 – создание малого производства.