Слайд 2
ПЛАН 1.Инерциальные системы отсчета. Первый закон Ньютона. Принцип относительности Галилея. 2.Масса тела. Плотность вещества. 3. Сила. Принцип суперпозиции сил. 4. Второй закон Ньютона для материальной точки в ИСО. 5. Третий закон Ньютона для материальных точек. 6. Закон всемирного тяготения: силы притяжения между точечными массами. Сила тяжести. Центр тяжести тела. Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R 0. 7. Движение небесных тел и их искусственных спутников. Первая космическая скорость. Вторая космическая скорость. 8. Сила упругости. Закон Гука. 9. Сила трения. Сухое трение. Сила трения скольжения. Сила трения покоя. Коэффициент трения. 10. Давление
Слайд 3: 1. Инерциальные системы отсчета
Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению). Инерция — явление сохранения состояния движения или покоя при отсутствии внешних воздействий. Движение по инерции — движение тела, происходящее без внешних воздействий. Принцип инерции : если на тело не действуют внешние силы, то оно сохраняет состояние покоя или равномерного прямолинейного движения. Инерциальная система отсчёта — система отсчёта, в которой тело, не взаимодействующее с другими телами, сохраняет состояние покоя или равномерного прямолинейного движения. Системы отсчёта, в которых принцип инерции не выполняется, называют неинерциальными.
Слайд 4: Первый закон Ньютона
Инерциальная система отсчёта Тело движется прямолинейно и равномерно Первый закон Ньютона Формулировка I. Материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее (его) изменить это состояние. Формулировка II. Существуют инерциальные системы отсчёта, в которых все тела в отсутствии внешних воздействий движутся прямолинейно и равномерно.
Слайд 5: Принцип относительности Галилея
Принцип относительности Галилея был сформулирован для механических явлений. Это означает, что при переходе от одной инерциальной системы отсчёта к другой математические формулы, описывающие законы механики, не изменяются. Все инерциальные системы отсчёта равноправны. Это положение было впервые установлено итальянским учёным Г. Галилеем в 1636 г . Принцип относительности Галилея. Во всех инерциальных системах отсчёта законы классической динамики имеют один и тот же вид.
Слайд 6: 2. Масса тела
Масса тела — физическая величина, являющаяся мерой инертности тела. Гравитационную массу m 1 (или m 2 ) определяют сравнением ее с массой эталонного тела – цилиндра из платино-иридиевого сплава, масса которого принята за 1 кг. Эталонное тело – цилиндр из платино-иридиевого сплава, масса которого принята за 1 кг Взвешивание на рычажных весах Процесс сравнения масс на рычажных весах называется взвешиванием. Единица измерения массы – килограмм ( кг ).
Слайд 7: Плотность вещества
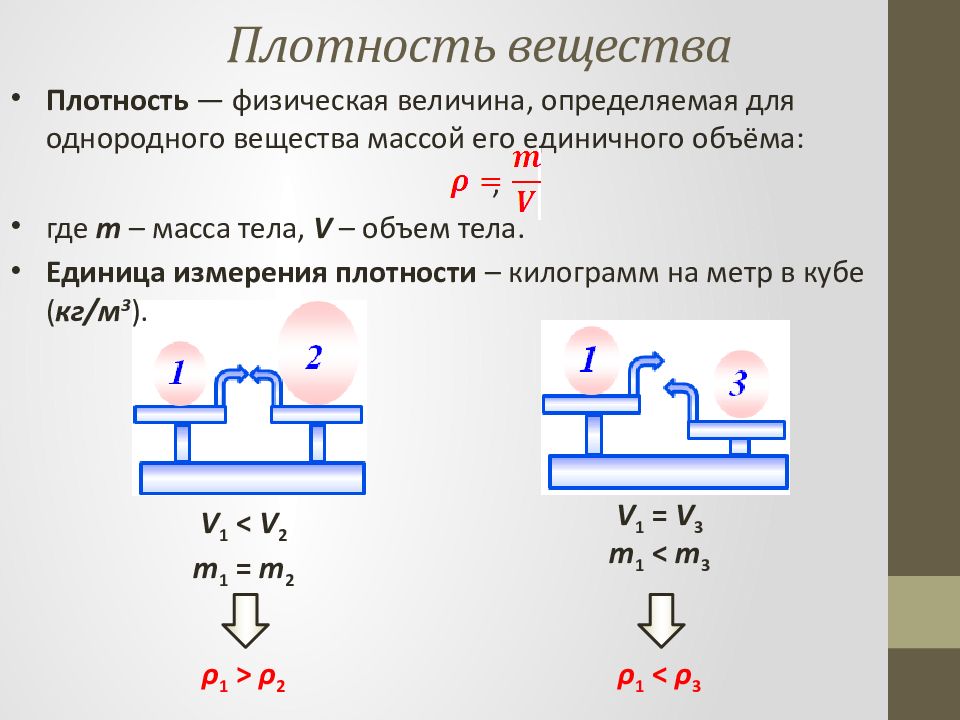
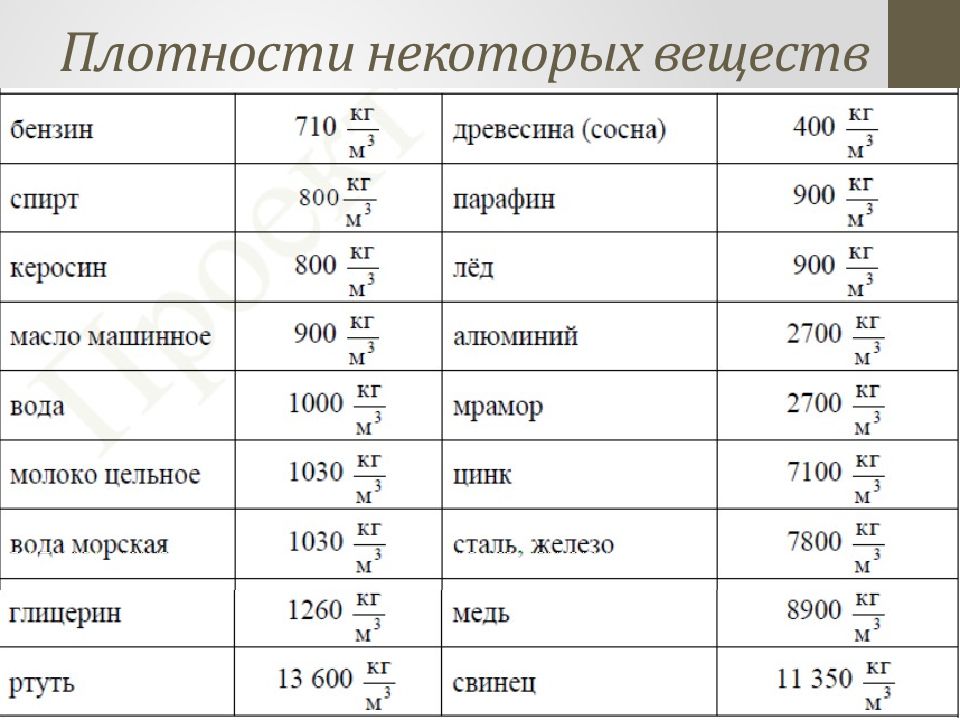
Плотность — физическая величина, определяемая для однородного вещества массой его единичного объёма: , где m – масса тела, V – объем тела. Единица измерения плотности – килограмм на метр в кубе ( кг/м 3 ). ρ 1 > ρ 2 ρ 1 < ρ 3 V 1 < V 2 m 1 = m 2 V 1 = V 3 m 1 < m 3
Слайд 9: 3. Сила
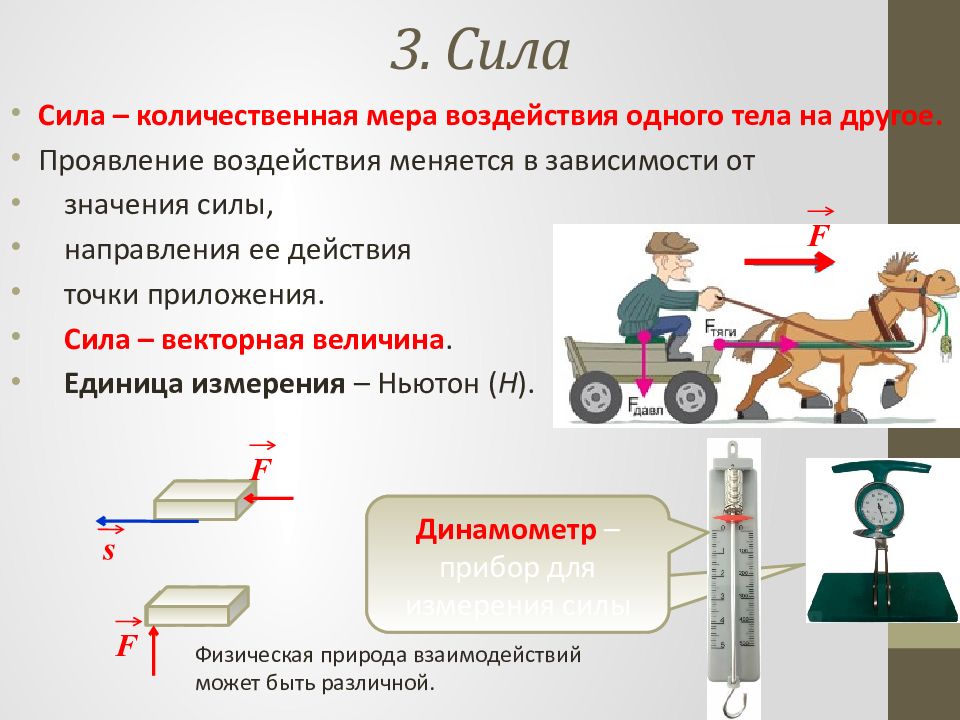
Динамометр – прибор для измерения силы 3. Сила Сила – количественная мера воздействия одного тела на другое. Проявление воздействия меняется в зависимости от значения силы, направления ее действия точки приложения. Сила – векторная величина. Единица измерения – Ньютон ( Н ). F s F F Динамометр – прибор для измерения силы Физическая природа взаимодействий может быть различной.
Слайд 10: Принцип суперпозиции сил
Воздействие на рассматриваемое тело других тел изображается векторами, число которых равно числу воздействующих тел. Равнодействующая нескольких сил – сила, эквивалентная данной системе сил, т.е. сила, вызывающая такое же механическое воздействие на рассматриваемое тело, что и система сил. - сила тяжести; - сила реакции опоры; - сила тяги; - сила трения.
Слайд 11: Принцип суперпозиции сил
Равнодействующая сила равна векторной сумме всех сил, приложенных к материальной точке. Принцип суперпозиции сил позволяет когда это удобно, рассматривать одну силу как сумму нескольких сил, называемых составляющими данной силы. - вес тела; - сила реакции опоры; - равнодействующая сила. P R
Слайд 12: 4. Второй закон Ньютона для материальной точки в ИСО
Формулировка I : В инерциальной системе отсчета ускорение тела прямо пропорционально векторной сумме всех действующих на тело сил и обратно пропорционально массе тела: где - ускорение тела, - равнодействующая сил,,, …,, действующих на тело, m - масса тела. Формулировка I I : Произведение массы тела и его ускорения равно векторной сумме всех действующих на него сил:
Слайд 13: 5. Третий закон Ньютона для материальных точек
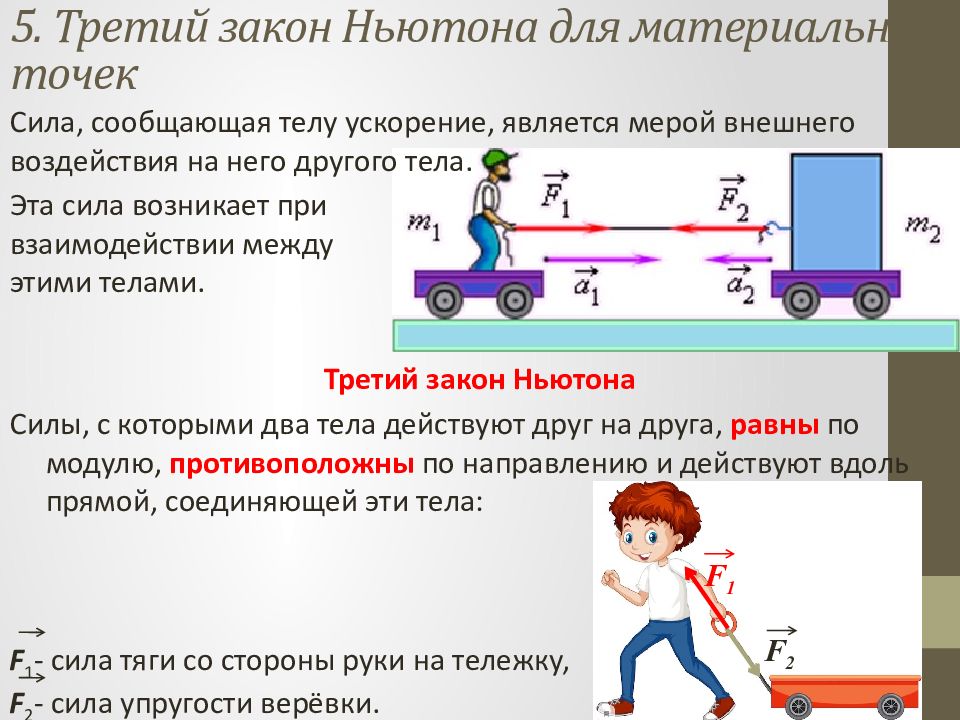
Сила, сообщающая телу ускорение, является мерой внешнего воздействия на него другого тела. Третий закон Ньютона Силы, с которыми два тела действуют друг на друга, равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей эти тела: Эта сила возникает при взаимодействии между этими телами. F 1 F 2 F 1 - сила тяги со стороны руки на тележку, F 2 - сила упругости верёвки.
Слайд 14: Третий закон Ньютона для материальных точек
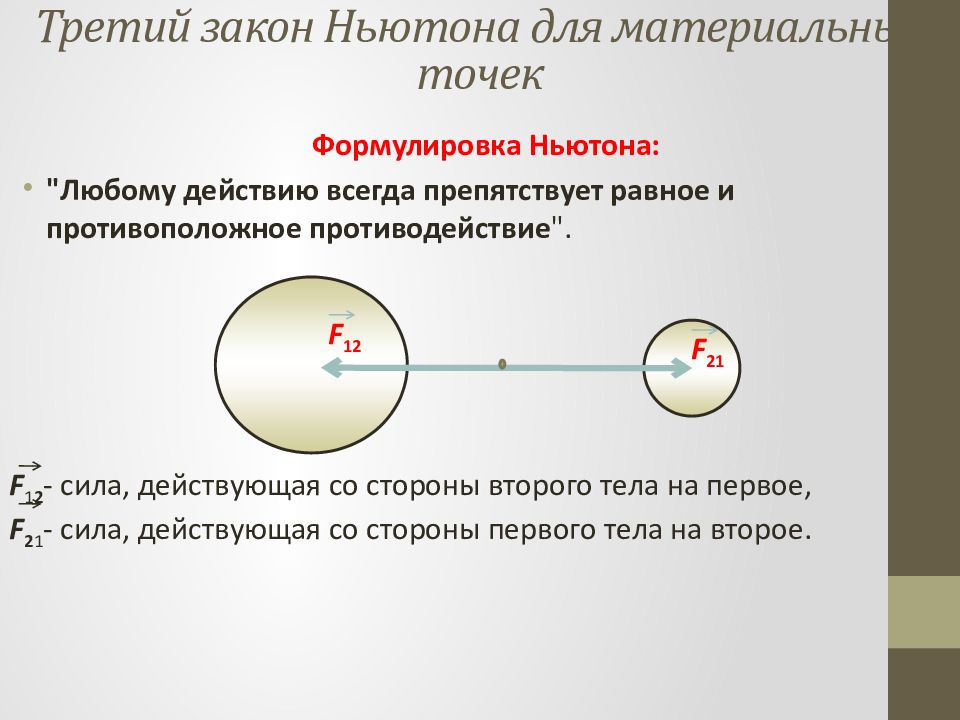
Формулировка Ньютона: "Любому действию всегда препятствует равное и противоположное противодействие ". F 1 2 - сила, действующая со стороны второго тела на первое, F 2 1 - сила, действующая со стороны первого тела на второе. F 12 F 21
Слайд 15: Применение законов Ньютона к решению задач
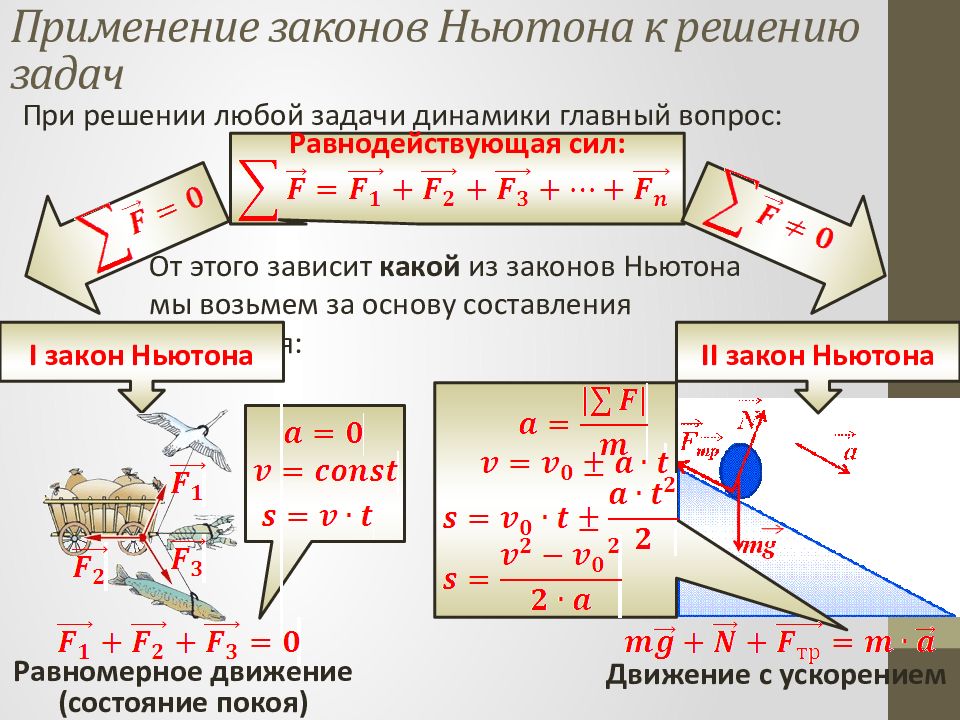
При решении любой задачи динамики главный вопрос: Равнодействующая сил: От этого зависит какой из законов Ньютона мы возьмем за основу составления уравнения: I закон Ньютона II закон Ньютона Равномерное движение (состояние покоя) Движение с ускорением
Слайд 16: 6. Закон всемирного тяготения: силы притяжения между точечными массами
Слово «гравитация» происходит от латинского слова gravitas, означающего «вес, тяжесть». Свободное падение тел на Землю объясняется наличием их притяжения к Земле. Закон всемирного тяготения : м ежду двумя любыми материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек, обратно пропорциональная квадрату расстояния между ними, направленная вдоль прямой, соединяющей материальные точки: где - гравитационная постоянная (коэффициент пропорциональности, одинаковый для всех тел), m 1 и m 2 - массы взаимодействующих тел, r - расстояние между ними. Закон был открыт И. Ньютоном в 1666 г.
Слайд 17: Гравитационная постоянная
Гравитационная постоянная численно равна силе гравитационного притяжения двух тел, массой по 1 кг каждое, находящихся на расстоянии 1 м одно от другого. Силы всемирного тяготения, действующие на два взаимодействующих тела. m 1 и m 2 - массы взаимодействующих тел, r - расстояние между ними.
Слайд 18: Сила тяжести
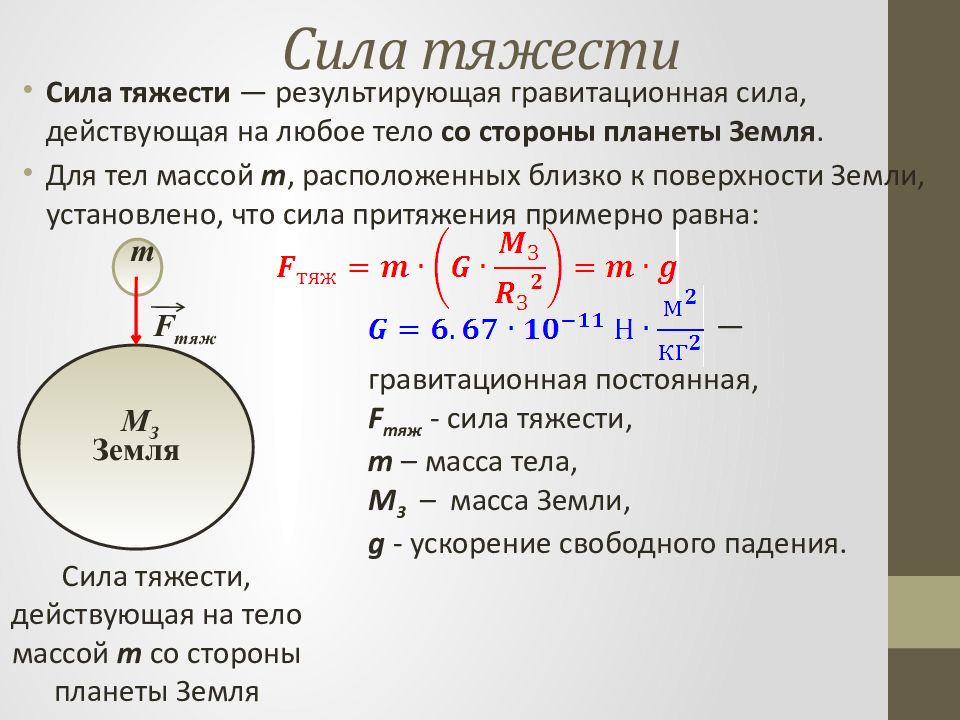
Сила тяжести — результирующая гравитационная сила, действующая на любое тело со стороны планеты Земля. Для тел массой m, расположенных близко к поверхности Земли, установлено, что сила притяжения примерно равна: m Земля M З F тяж Сила тяжести, действующая на тело массой m со стороны планеты Земля гравитационная постоянная, F тяж - сила тяжести, m – масса тела, M З – масса Земли, g - ускорение свободного падения. —
Слайд 19: Ускорение свободного падения
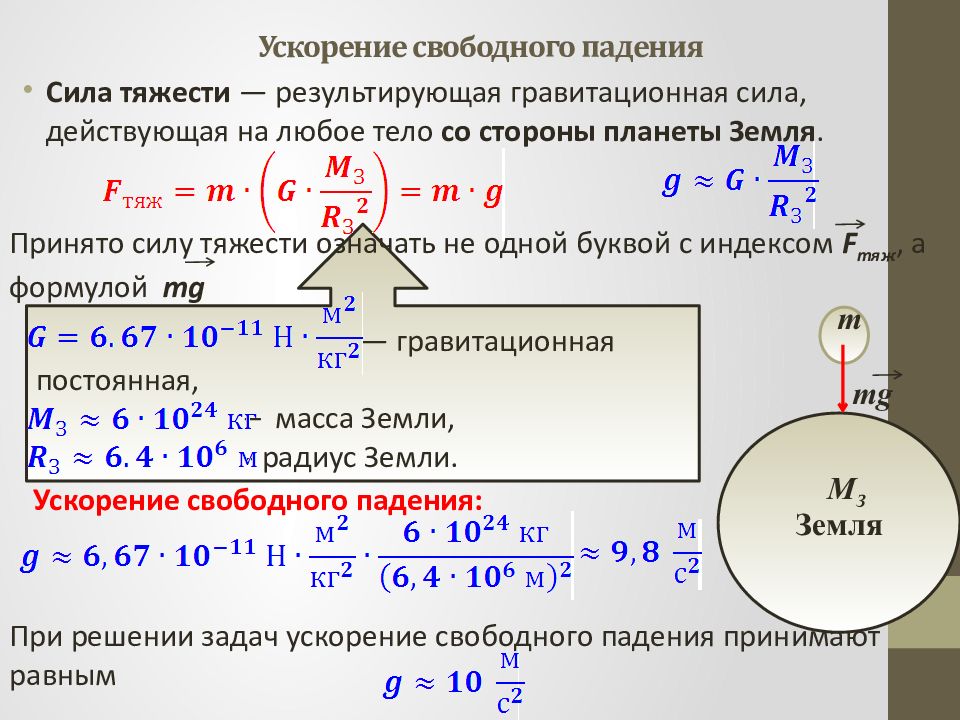
Сила тяжести — результирующая гравитационная сила, действующая на любое тело со стороны планеты Земля. m Земля M З mg Принято силу тяжести означать не одной буквой с индексом F тяж, а формулой mg — гравитационная постоянная, – масса Земли, - радиус Земли. Ускорение свободного падения: При решении задач ускорение свободного падения принимают равным
Слайд 20: Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R 0
где — гравитационная постоянная, m – масса тела, M З - масса Земли, R 0 - радиус Земли, - ускорение свободного падения на расстояние h от поверхности Земли. Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R 0 При удалении от поверхности Земли сила тяжести, а также ускорение свободного падения, уменьшается. Если тело находится на расстояние h от поверхности Земли, то силу тяжести будем искать по формуле:
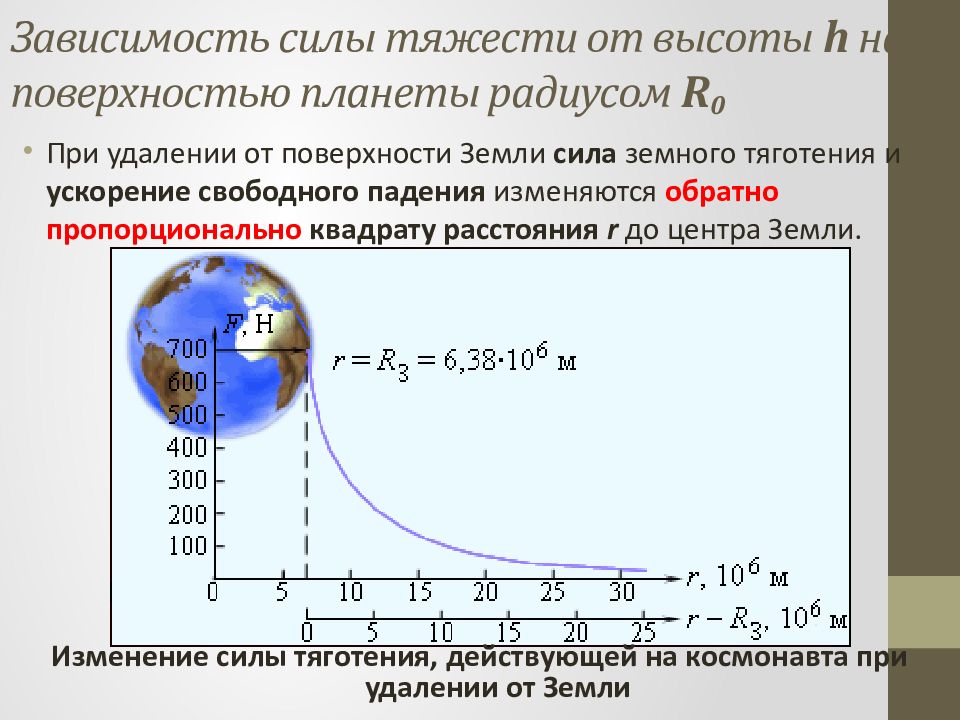
Слайд 21: Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R 0
Изменение силы тяготения, действующей на космонавта при удалении от Земли Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R 0 При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли.
Слайд 22: 7. Движение небесных тел и их искусственных спутников
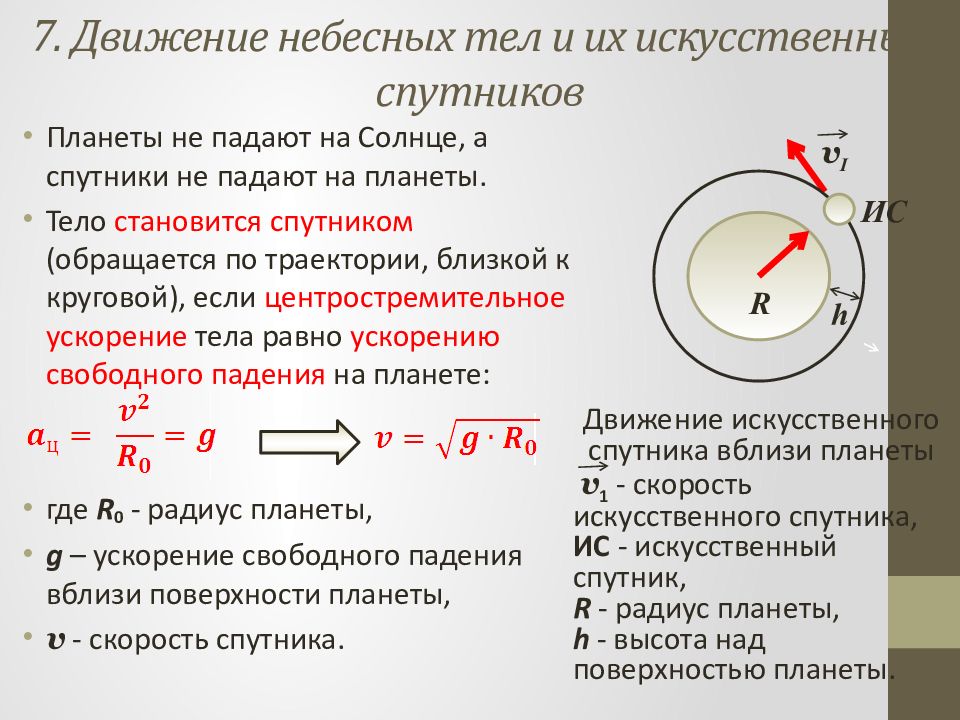
Планеты не падают на Солнце, а спутники не падают на планеты. Тело становится спутником (обращается по траектории, близкой к круговой), если центростремительное ускорение тела равно ускорению свободного падения на планете: где R 0 - радиус планеты, g – ускорение свободного падения вблизи поверхности планеты, v - скорость спутника. Движение искусственного спутника вблизи планеты v 1 - скорость искусственного спутника, ИС - искусственный спутник, R - радиус планеты, h - высота над поверхностью планеты. v I R h ИС
Слайд 23: Первая космическая скорость
Первая космическая (круговая) скорость — минимальная скорость, которую надо сообщить телу у поверхности Земли (или небесного тела), чтобы тело могло двигаться вокруг Земли (или небесного тела) по круговой орбите. Первая космическая скорость для планеты Земля : Движение искусственного спутника вблизи планеты v 1 - скорость искусственного спутника, ИС - искусственный спутник, R - радиус планеты, h - высота над поверхностью планеты. v I R h ИС где - радиус Земли, - ускорение свободного падения.
Слайд 24: Первая космическая скорость
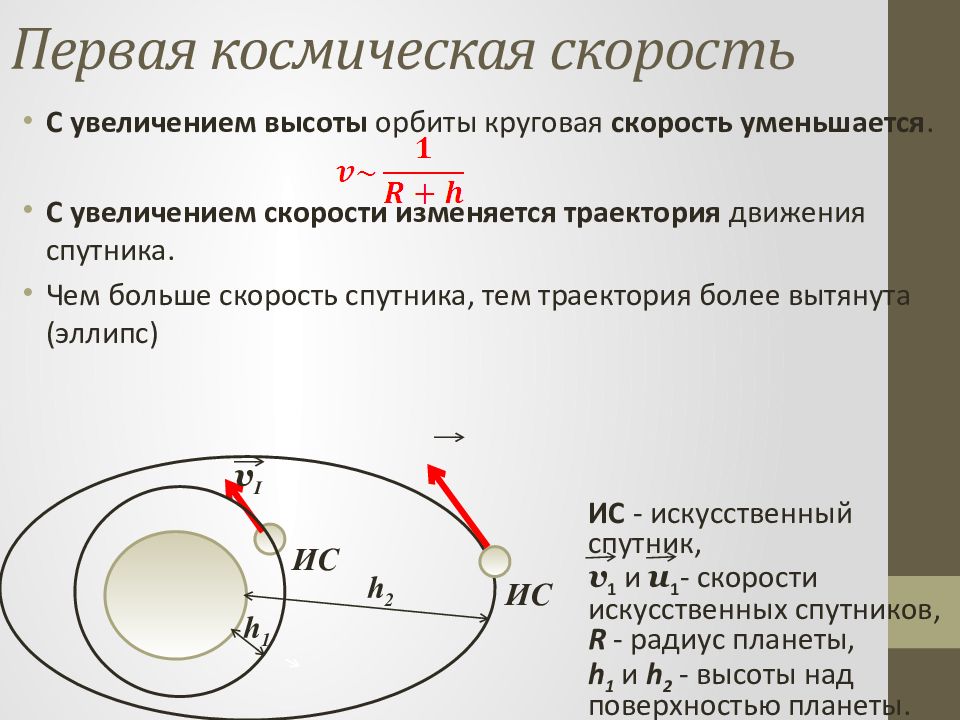
С увеличением высоты орбиты круговая скорость уменьшается. С увеличением скорости изменяется траектория движения спутника. Чем больше скорость спутника, тем траектория более вытянута (эллипс) v I ИС ИС h 1 h 2 ИС - искусственный спутник, v 1 и u 1 - скорости искусственных спутников, R - радиус планеты, h 1 и h 2 - высоты над поверхностью планеты.
Слайд 25: Зависимость траектории спутника от скорости его движения
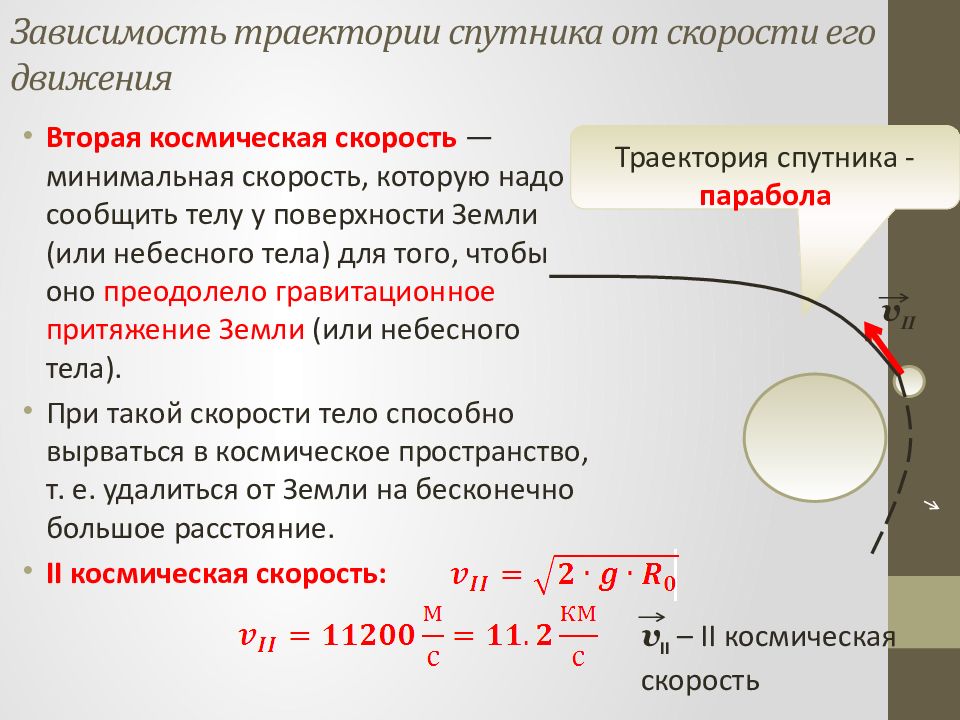
Вторая космическая скорость — минимальная скорость, которую надо сообщить телу у поверхности Земли (или небесного тела) для того, чтобы оно преодолело гравитационное притяжение Земли (или небесного тела). При такой скорости тело способно вырваться в космическое пространство, т. е. удалиться от Земли на бесконечно большое расстояние. II космическая скорость: Траектория спутника - парабола v II v II – II космическая скорость
Слайд 26: Зависимость траектории спутника от скорости его движения
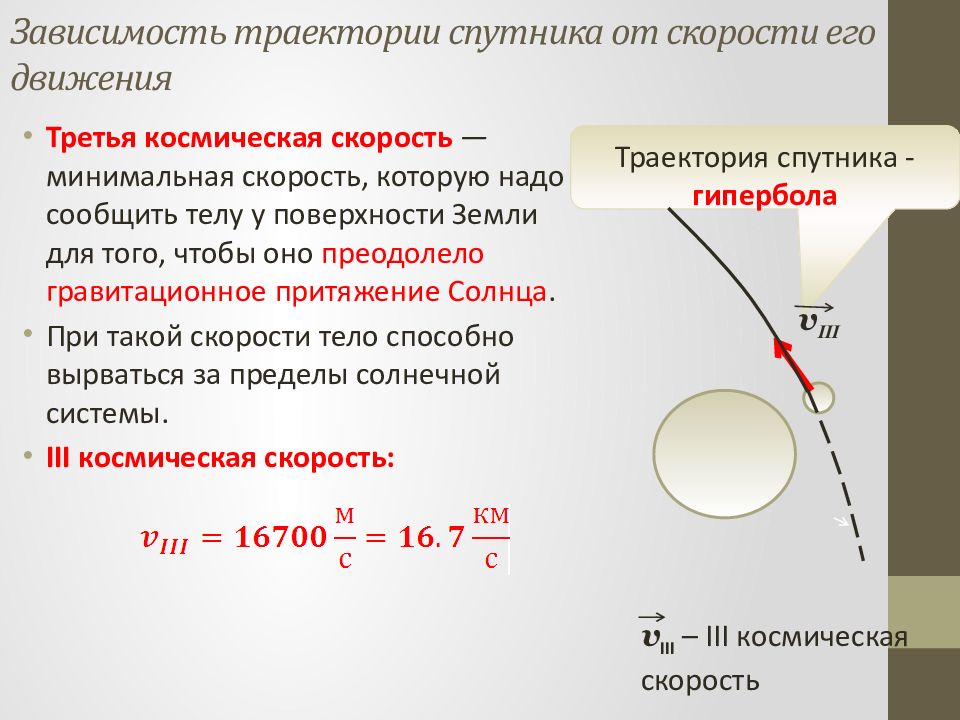
Третья космическая скорость — минимальная скорость, которую надо сообщить телу у поверхности Земли для того, чтобы оно преодолело гравитационное притяжение Солнца. При такой скорости тело способно вырваться за пределы солнечной системы. III космическая скорость: Траектория спутника - гипербола v III v III – III космическая скорость
Слайд 27: 8. Сила упругости. Закон Гука
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил. Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими, а деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело, - пластическими. Упругая деформация Пластическая деформация
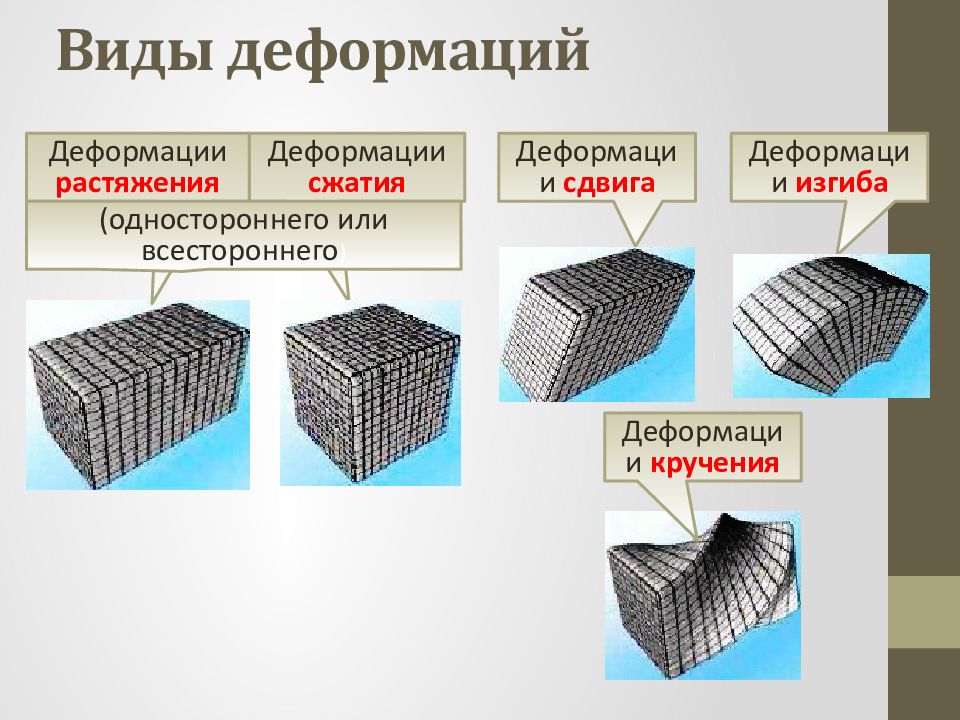
Слайд 28: Виды деформаций
Деформации сжатия Деформации изгиба Деформации сдвига Деформации растяжения (одностороннего или всестороннего ) Деформации кручения
Слайд 29: Сила упругости
Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Сила упругости F упр mg Δ x mg – сила тяжести, действующая на брусок массой m, P – сила, действующая на перекладину вследсвие действия силы тяжести и вызывающая деформацию Δ x F упр – противодействующая сила – сила упругости. P
Слайд 30: Силы упругости
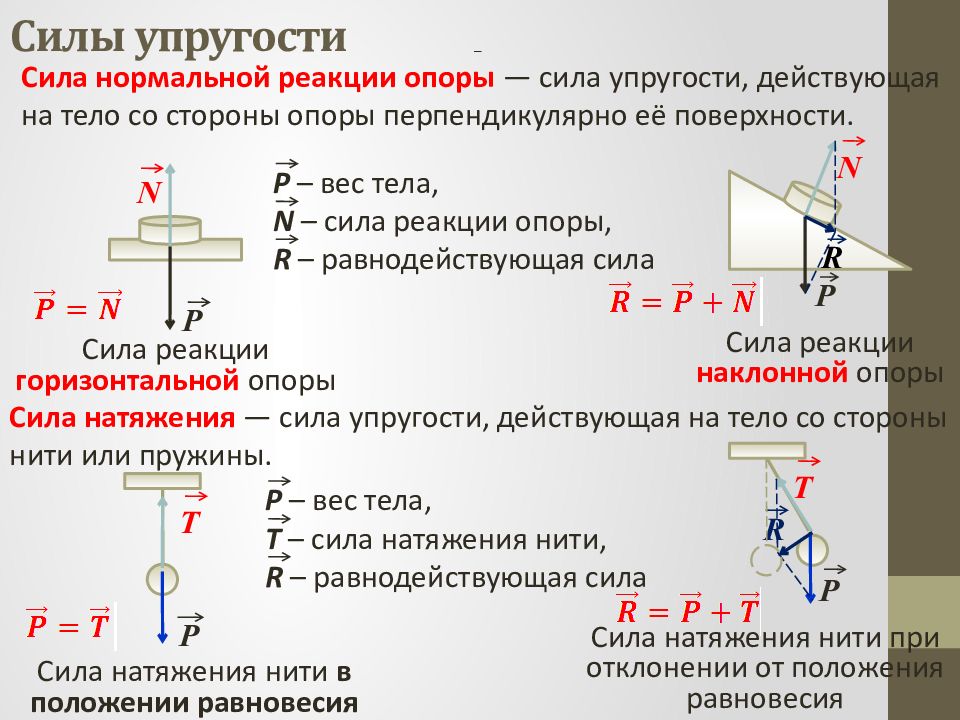
Сила нормальной реакции опоры — сила упругости, действующая на тело со стороны опоры перпендикулярно её поверхности. N P P N R Сила реакции горизонтальной опоры Сила реакции наклонной опоры P – вес тела, N – сила реакции опоры, R – равнодействующая сила Сила натяжения — сила упругости, действующая на тело со стороны нити или пружины. Сила натяжения нити в положении равновесия Сила натяжения нити при отклонении от положения равновесия P T P – вес тела, T – сила натяжения нити, R – равнодействующая сила P T R –
Слайд 31: 1.2.8. Сила упругости
Сила упругости F упр - сила, возникающая при деформации тела (нить, пружина, трос и др.) и восстанавливающая первоначальные размеры и форму тела при прекращении внешнего воздействия где k - коэффициент жесткости или просто жесткость пружины (единица измерения ), ∆ x или чаще ее обозначают x – растяжение (сжатие) пружины или нити (единица измерения ). Знак «-» показывает, что сила упругости всегда направлена противоположно деформации тела. Сила упругости, как и все силы, измеряется в ньютонах ( Н ).
Слайд 32: 8. Закон Гука
Модуль силы упругости F упр, возникающей при деформации тела, пропорционален его удлинению ∆ l : где k - жесткость пружины, ∆ l – (имеет тот же смысл, что и ∆ x ) - растяжение (сжатие); В задачах могут встречаться три обозначения одной величины «растяжение»: ∆ l, ∆ x,. x. Коэффициент жесткости зависит от длины пружины. Эта зависимость обратно пропорциональная : длинную резинку натянуть легче чем короткую. от площади поперечного сечения упругого стержня. Эта зависимость прямо пропорциональная : толстую резинку натянуть труднее чем тонкую.
Слайд 33: 8. Закон Гука
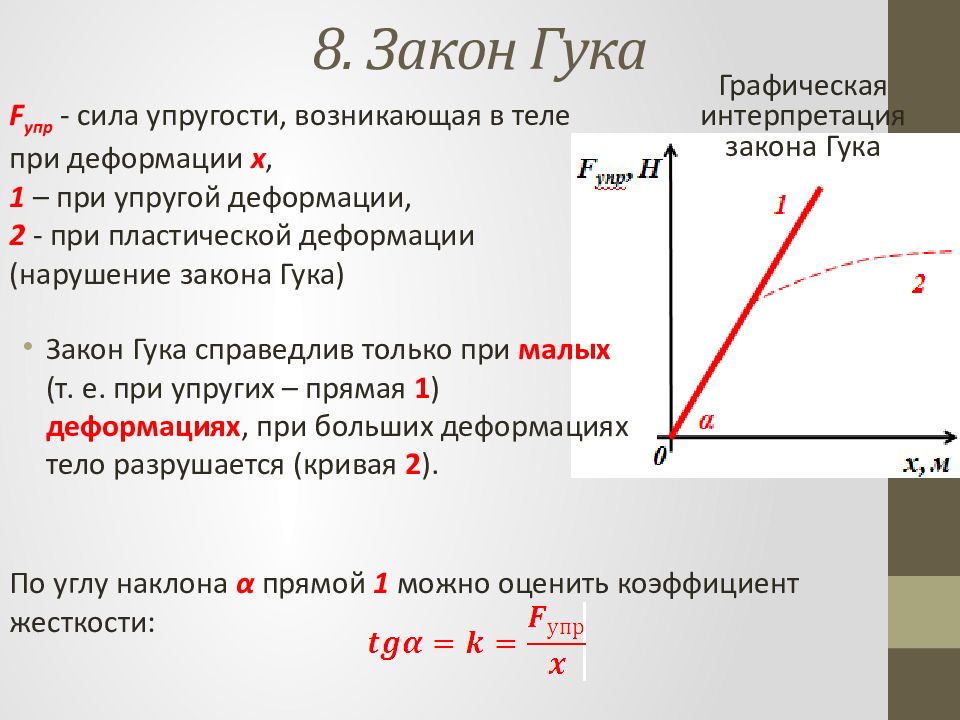
Закон Гука справедлив только при малых (т. е. при упругих – прямая 1 ) деформациях, при больших деформациях тело разрушается (кривая 2 ). Графическая интерпретация закона Гука F упр - сила упругости, возникающая в теле при деформации x, 1 – при упругой деформации, 2 - при пластической деформации (нарушение закона Гука) По углу наклона α прямой 1 можно оценить коэффициент жесткости:
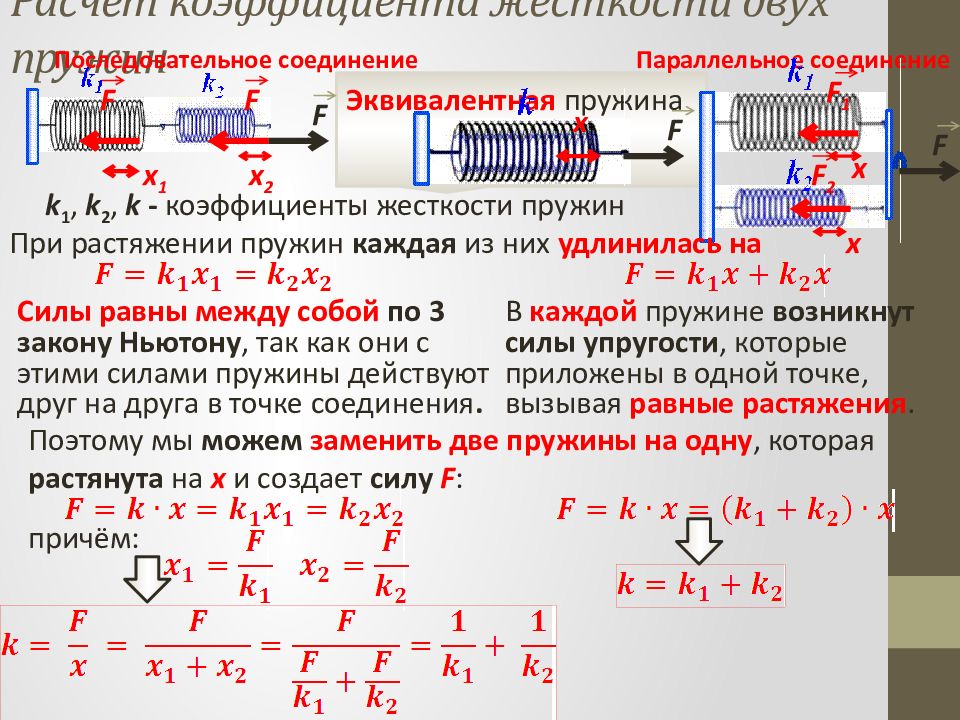
Слайд 34: Расчет коэффициента жесткости двух пружин
Последовательное соединение Силы равны между собой по 3 закону Ньютону, так как они с этими силами пружины действуют друг на друга в точке соединения. Параллельное соединение В каждой пружине возникнут силы упругости, которые приложены в одной точке, вызывая равные растяжения. Эквивалентная пружина k 1, k 2, k - коэффициенты жесткости пружин При растяжении пружин каждая из них удлинилась на F F F F F 1 F 2 x x x 1 x 2 Поэтому мы можем заменить две пружины на одну, которая растянута на х и создает силу F : F x причём:
Слайд 35: Динамометр
Как следует из закона Гука, по удлинению пружины можно судить о силе, действующей на неё. Этот факт используется для измерения сил с помощью динамометра — пружины с линейной шкалой, проградуированной в единицах силы. Для измерения силы обычно используют специальное устройство называемое динамометром. Динамометр – прибор для измерения силы
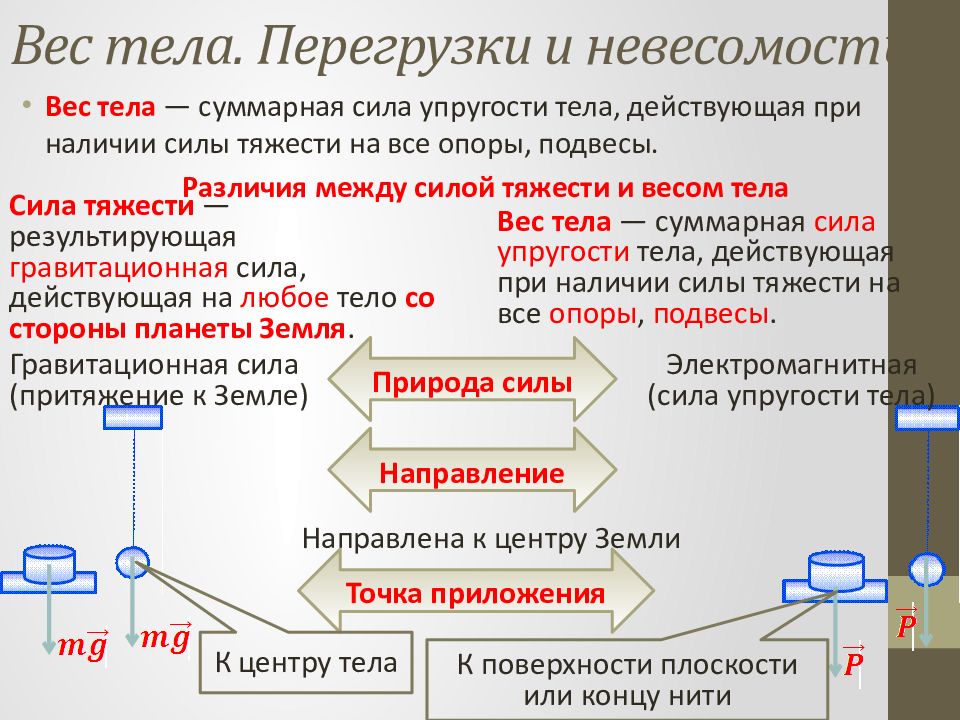
Слайд 36: Вес тела. Перегрузки и невесомость
Вес тела — суммарная сила упругости тела, действующая при наличии силы тяжести на все опоры, подвесы. Различия между силой тяжести и весом тела Сила тяжести — результирующая гравитационная сила, действующая на любое тело со стороны планеты Земля. Вес тела — суммарная сила упругости тела, действующая при наличии силы тяжести на все опоры, подвесы. Природа силы Гравитационная сила (притяжение к Земле) Электромагнитная (сила упругости тела) Направление Направлена к центру Земли Точка приложения К центру тела К поверхности плоскости или концу нити
Слайд 37
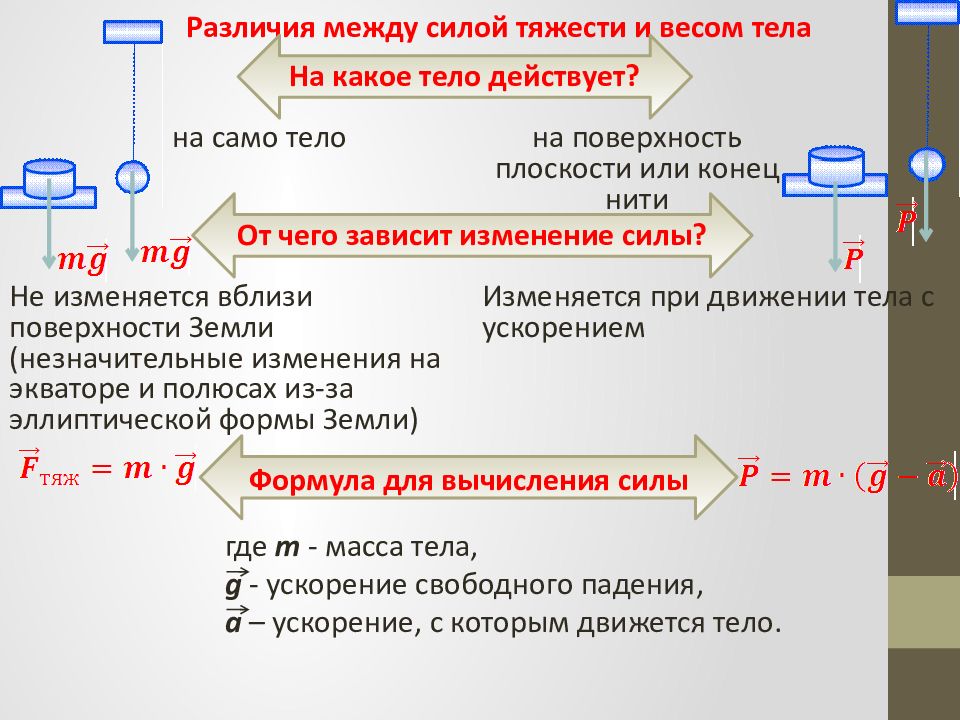
Различия между силой тяжести и весом тела На какое тело действует? на само тело на поверхность плоскости или конец нити От чего зависит изменение силы? Не изменяется вблизи поверхности Земли (незначительные изменения на экваторе и полюсах из-за эллиптической формы Земли) Формула для вычисления силы Изменяется при движении тела с ускорением где m - масса тела, g - ускорение свободного падения, a – ускорение, с которым движется тело.
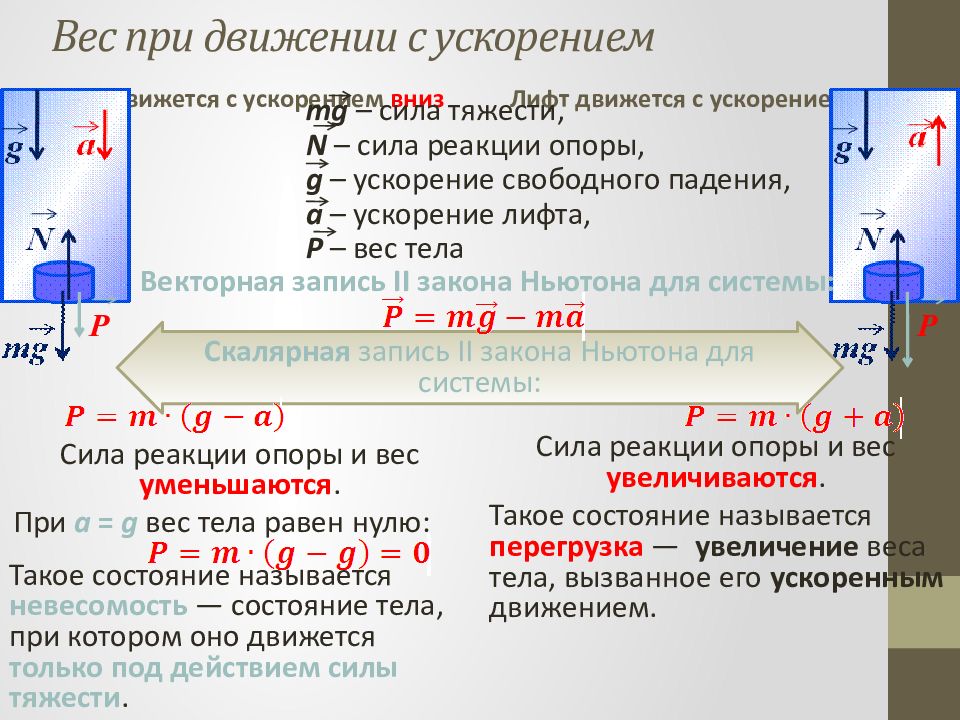
Слайд 38: Вес при движении с ускорением
Лифт движется с ускорением вниз Лифт движется с ускорением вверх P P mg – сила тяжести, N – сила реакции опоры, g – ускорение свободного падения, a – ускорение лифта, P – вес тела Скалярная запись II закона Ньютона для системы: Векторная запись II закона Ньютона для системы: Сила реакции опоры и вес уменьшаются. Сила реакции опоры и вес увеличиваются. При a = g вес тела равен нулю: Такое состояние называется невесомость — состояние тела, при котором оно движется только под действием силы тяжести. Такое состояние называется перегрузка — увеличение веса тела, вызванное его ускоренным движением.
Слайд 39: 9. Сила трения
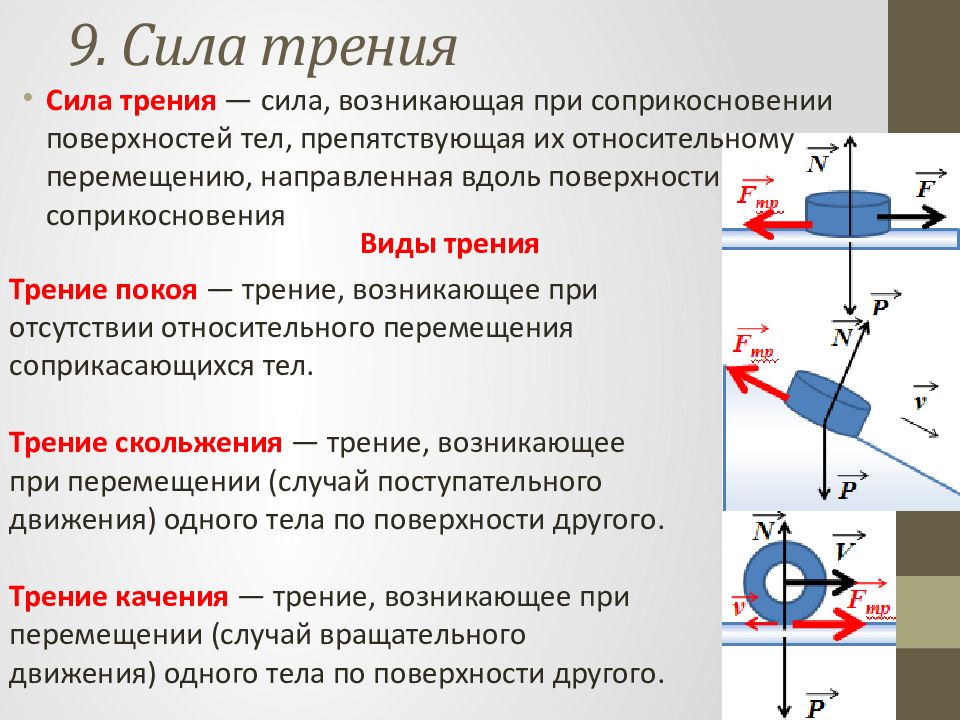
Сила трения — сила, возникающая при соприкосновении поверхностей тел, препятствующая их относительному перемещению, направленная вдоль поверхности соприкосновения Виды трения Трение покоя — трение, возникающее при отсутствии относительного перемещения соприкасающихся тел. Трение скольжения — трение, возникающее при перемещении (случай поступательного движения) одного тела по поверхности другого. Трение качения — трение, возникающее при перемещении (случай вращательного движения) одного тела по поверхности другого.
Слайд 40: Трение покоя
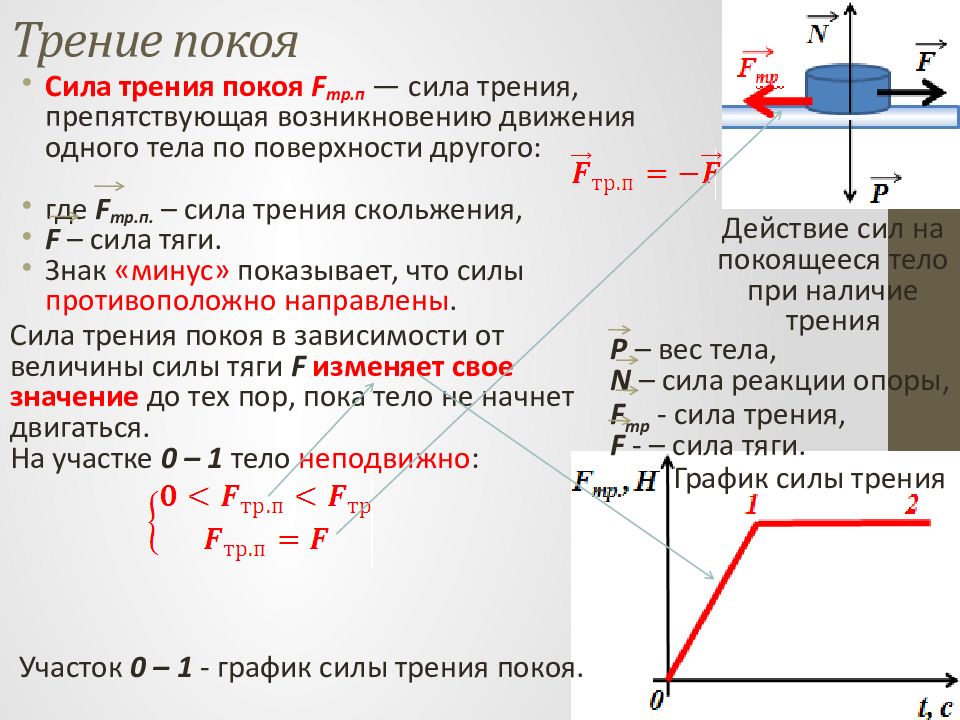
Сила трения покоя F тр.п — сила трения, препятствующая возникновению движения одного тела по поверхности другого: где F тр.п. – сила трения скольжения, F – сила тяги. Знак «минус» показывает, что силы противоположно направлены. Действие сил на покоящееся тело при наличие трения P – вес тела, N – сила реакции опоры, F тр - сила трения, F - – сила тяги. Сила трения покоя в зависимости от величины силы тяги F изменяет свое значение до тех пор, пока тело не начнет двигаться. На участке 0 – 1 тело неподвижно : График силы трения Участок 0 – 1 - график силы трения покоя.
Слайд 41: Трение скольжения
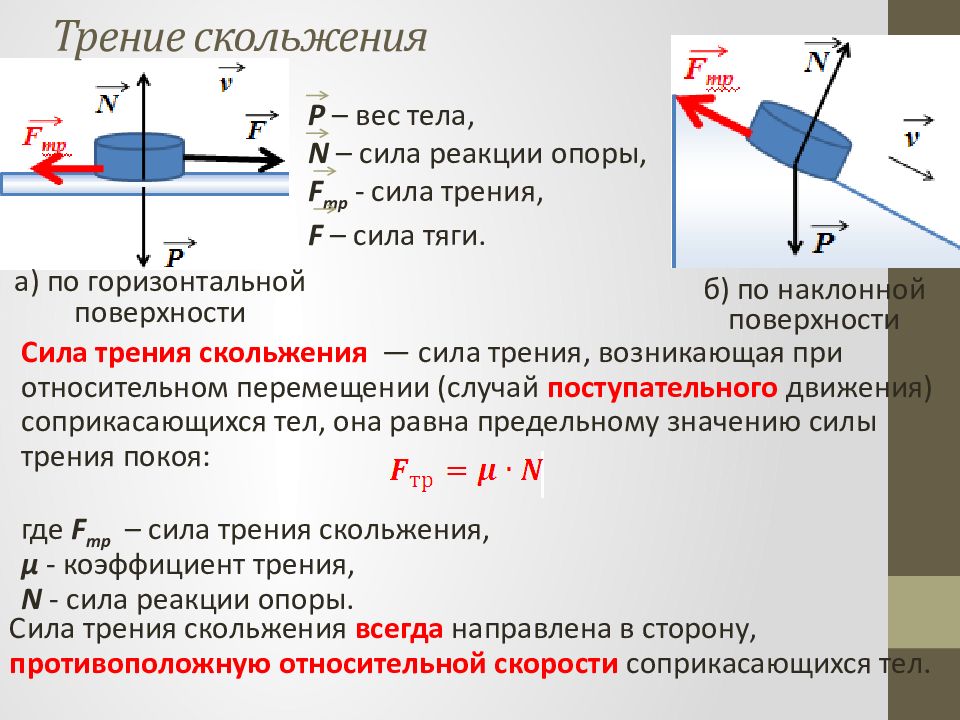
Сила трения скольжения — сила трения, возникающая при относительном перемещении (случай поступательного движения) соприкасающихся тел, она равна предельному значению силы трения покоя: где F тр – сила трения скольжения, μ - коэффициент трения, N - сила реакции опоры. P – вес тела, N – сила реакции опоры, F тр - сила трения, F – сила тяги. Сила трения скольжения всегда направлена в сторону, противоположную относительной скорости соприкасающихся тел. а) по горизонтальной поверхности б) по наклонной поверхности
Слайд 42: Трение скольжения
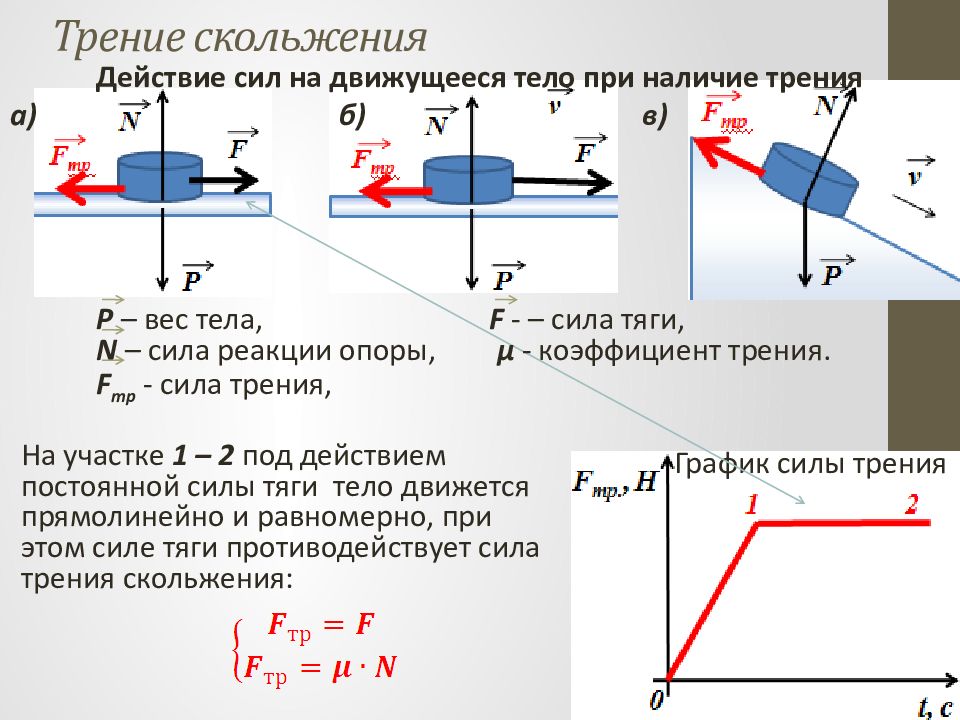
График силы трения Трение скольжения На участке 1 – 2 под действием постоянной силы тяги тело движется прямолинейно и равномерно, при этом силе тяги противодействует сила трения скольжения: P – вес тела, N – сила реакции опоры, F тр - сила трения, а) б) в) F - – сила тяги, μ - коэффициент трения. Действие сил на движущееся тело при наличие трения
Слайд 43: Трение качения
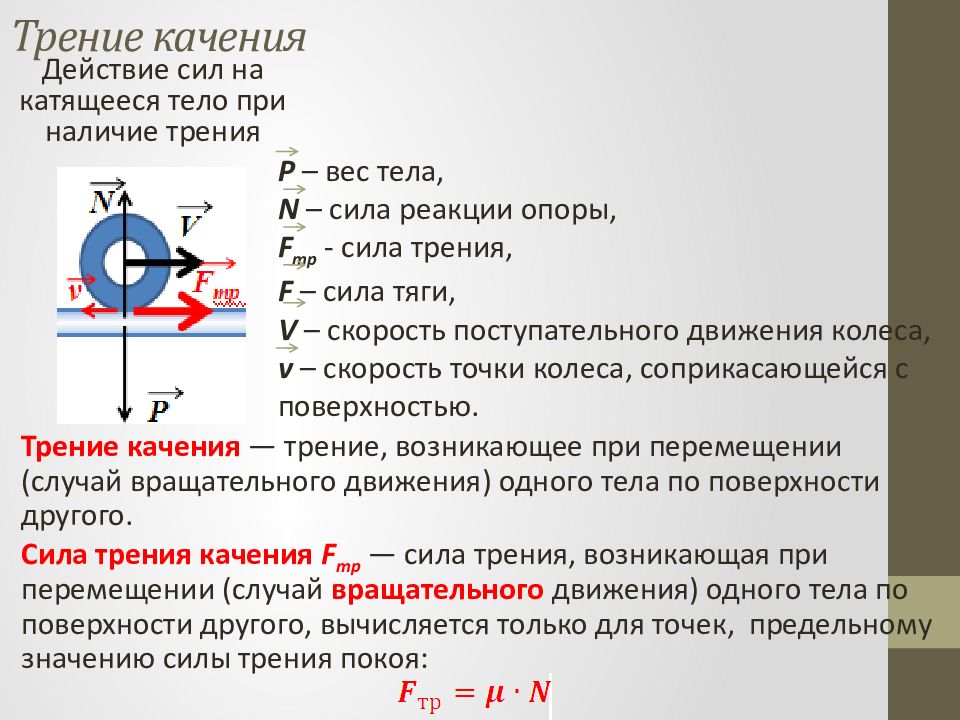
Трение качения — трение, возникающее при перемещении (случай вращательного движения) одного тела по поверхности другого. Сила трения качения F тр — сила трения, возникающая при перемещении (случай вращательного движения) одного тела по поверхности другого, вычисляется только для точек, предельному значению силы трения покоя: P – вес тела, N – сила реакции опоры, F тр - сила трения, F – сила тяги, V – скорость поступательного движения колеса, v – скорость точки колеса, соприкасающейся с поверхностью. Действие сил на катящееся тело при наличие трения
Слайд 44: 10. Давление
Давление - величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности: где F - сила давления тела, S – площадь поверхности тела, единица измерения – метр квадратный ( м 2 ). Действие силы на поверхность Единица измерения Па ( Паскаль ), Давление - величина скалярная, у давления нет направления. Обратите внимание! Любая поверхность выдерживает только определенное давление. Если это давление будет выше, то опора разрушается. ... давление гусеничного трактора массой 6,7 тонны на почву составляет 47000 Па ... втыкая пальцем иглу или булавку в ткань, мы создаем давление около 100 000 000 Па ... когда жалит оса, то она оказывает на кожу человека давление 30 000 000 000 Па.
Слайд 45: Давление
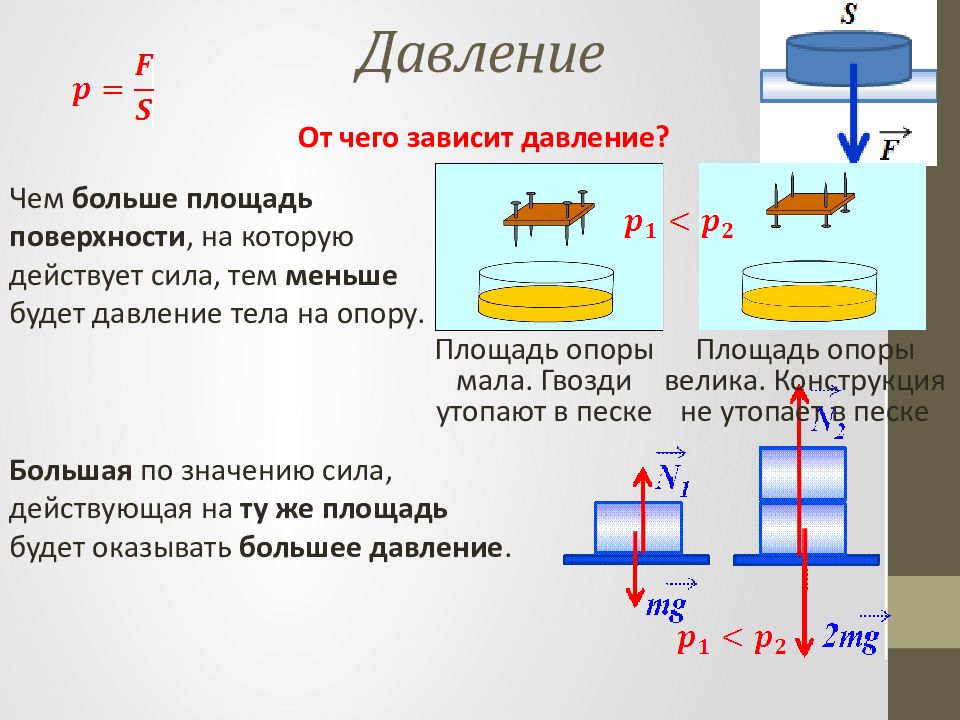
От чего зависит давление? Чем больше площадь поверхности, на которую действует сила, тем меньше будет давление тела на опору. Большая по значению сила, действующая на ту же площадь будет оказывать большее давление. Площадь опоры мала. Гвозди утопают в песке Площадь опоры велика. Конструкция не утопает в песке
Слайд 46: Способы изменения давления
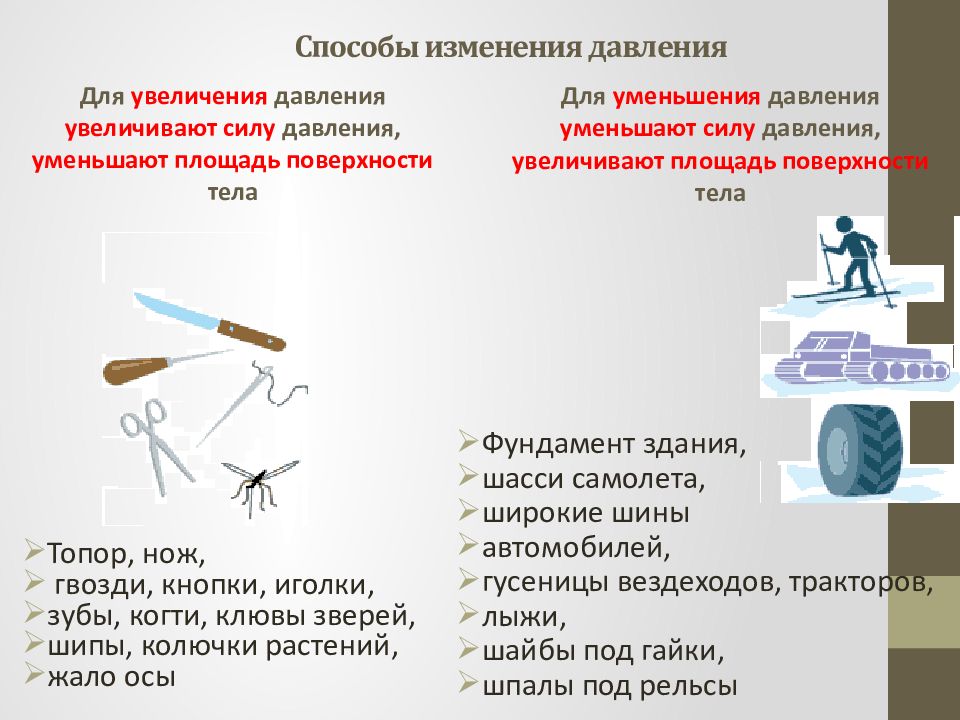
Для увеличения давления увеличивают силу давления, уменьшают площадь поверхности тела Топор, нож, гвозди, кнопки, иголки, зубы, когти, клювы зверей, шипы, колючки растений, жало осы Для уменьшения давления уменьшают силу давления, увеличивают площадь поверхности тела Фундамент здания, шасси самолета, широкие шины автомобилей, гусеницы вездеходов, тракторов, лыжи, шайбы под гайки, шпалы под рельсы
Последний слайд презентации: Динамика: Это интересно…
Если вылить содержимое яйца, а для опыта оставить скорлупу, то можно попробовать проткнуть ее иголкой изнутри и снаружи. Изнутри - легче, снаружи - тяжелее. Результат при одинаковых усилиях будет зависеть от формы скорлупы: выпуклая или вогнутая. Поэтому маленький цыпленок легко разбивает скорлупу изнутри, а снаружи он защищен более надежно. Свойство выпуклых форм лучше выдерживать нагрузку позволяет архитекторам проектировать куполообразные крыши, мосты, потолки, т.к. они прочнее плоских !