Слайд 2
Индекс - уақыт ішінде, кеңістікте немесе жоспармен кез-келген әлеуметтік – экономикалық құбылыстардың шамасының қатынасын көрсететін қатысты шама
Слайд 3: Экономи калық индекстер
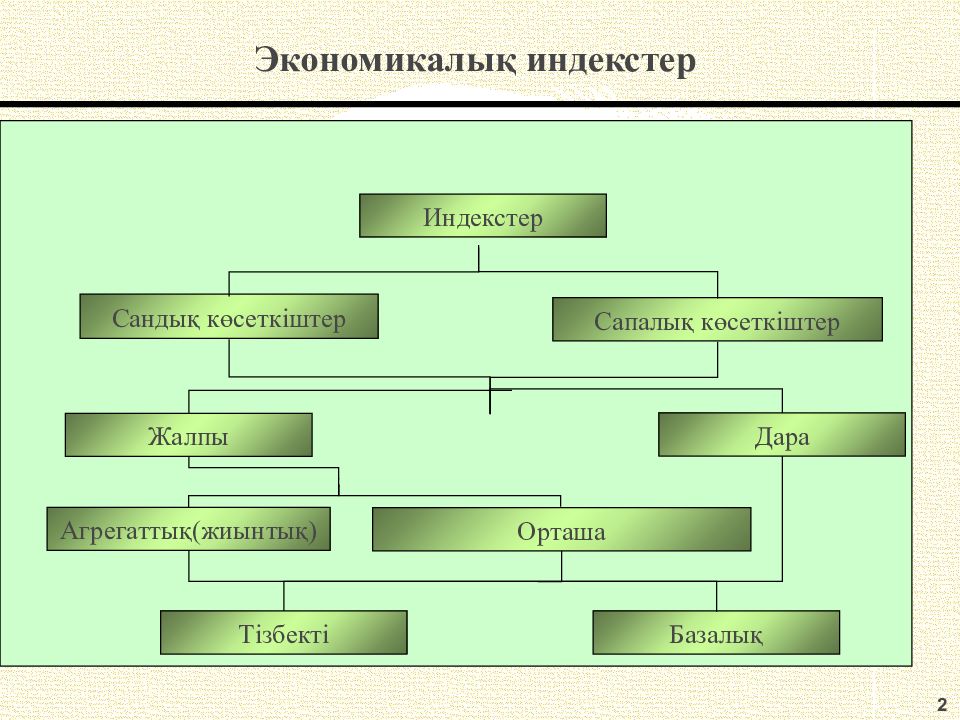
2 Экономи калық индекстер Индекстер Сандық көсеткіштер Сапалық көсеткіштер Дара Агрегаттық(жиынтық ) Орташа Базалық Тізбекті Жалпы
Слайд 4: Шарты белгілеулер
q -өнім көлемі p- тауар бағасы pq - тауар айналымы z- өнімнің өзіндік құны zq - барлық өнімге жұмсалған шығын w- еңбек өнімділігі t- бір өнімге жұмсалған уақыт T- жалпы уақыт шығыны ( T= tq ) i - дара индекс I -жалпы индекс
Слайд 5: Дара индекстер ж иынтықтың тек бір элементінің өзгерісін сипаттайды
3 Дара индекстер ж иынтықтың тек бір элементінің өзгерісін сипаттайды 1. Бағаның дара индексі : 2. Өнімнің физикалық көлемінің дара индексі : 3. Тауар айналымының дара индексі :
Слайд 6: Дара индекстер
4 Дара индекстер 4. Өзіндік құнның дара индексі : 5. Еңбек өнімділігінің дара индексі :
Слайд 7: Дара индекстер
6. Өндіріс шығындарының дара индексі 7. Еңбек сыйымдылығының дара индексі
Слайд 8: Тапсырма 1
Машина жасау зауытының 2 тоқсанда шығарған өнім көлемі кестеде : Өнім түрі Шығарылған өнім, дана. Бір дана бағасы, ш.б I тоқ. (q 0 ) II тоқ. (q 1 ) I тоқ. (p 0 ) II тоқ. (p 1 ) Автомобиль А моделі 2500 2610 4,8 5,4 Автомобиль В моделі 3000 2950 7,1 7,6 Автомобиль С моделі 3600 3700 5,0 5,7
Слайд 9: Тапсырма 1. Әр өнім түрі бойынша шығарылған өнімнің (%-бен) өзгерісін анықтау қажет
А автомобилінің өндірісі ағымдағы жылы өткен жылмен салыстырғанда 104,4%, яғни 4,4% ға өсті В автомобилінің өндірісі 98,3%, яғни 1,7% қысқарды
Слайд 11: Тапсырма 1 Әр өнім түрі бойынша бағаның (%-бен) өзгерісін анықтау қажет
А модельді автомобиль үшін немесе 112,5% Баға 12,5% (112,5-100) өсті
Слайд 13: Тапсырма 1
С модельді автомобиль үшін немесе 114,0%, яғни баға 14,0% өсті
Слайд 14
Жалпы индекстер күрделі құбылыстың барлық элементтерінің өзгерісін сипаттайды, басқаша айтқанда олар салыстыруға келмейтін элементтерден тұратын күрделі әлеуметтік-экономикалық құбылыс деңгейлерінің қатынасын көрсетеді.
Слайд 15
Агрегаттық индекстер 2 элементтен тұрады: Индексі есептелетін шама; Индекс салмағы х 1,х 0 - индексі есептелетін шаманың есепті және базалық мәндері (өзгермелі шама) f- индекс салмағы (тұрақты шама)
Слайд 17: Агрегаттық (жиынтық ) индекстер
5 Агрегаттық (жиынтық ) индекстер 1. Агрегаттық баға индексі а) Ласпейрес бойынша : б) Пааше бойынша :
Слайд 18: Агрегаттық (жиынтық ) индекстер
6 Агрегаттық (жиынтық ) индекстер 2. Өнімнің физикалық көлемінің агрегаттық индексі немесе
Слайд 19: Агрегаттық (жиынтық ) индекстер
7 Агрегаттық (жиынтық ) индекстер 3. Тауар айналымының агрегаттық индексі
Слайд 20: Агрегаттық (жиынтық ) индекстер
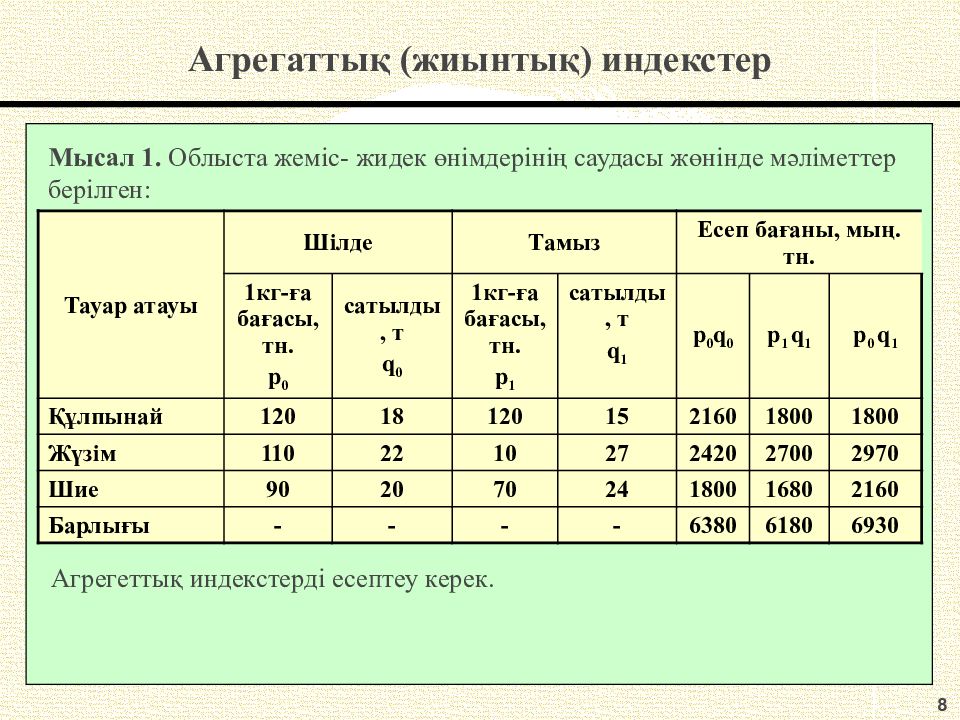
8 Агрегаттық (жиынтық ) индекстер Мысал 1. Облыста жеміс - жидек өнімдерінің саудасы жөнінде мәліметтер берілген : Тауар атауы Шілде Тамыз Есеп бағаны, мың. тн. 1кг-ға бағасы, тн. p 0 сатылды, т q 0 1кг-ға бағасы, тн. p 1 сатылды, т q 1 p 0 q 0 p 1 q 1 p 0 q 1 Құлпынай 120 18 120 15 2160 1800 1800 Жүзім 110 22 10 27 2420 2700 2970 Шие 90 20 70 24 1800 1680 2160 Барлығы - - - - 6380 6180 6930 Агрегеттық индекстерді есептеу керек.
Слайд 21: Агрегаттық (жиынтық ) индекстер
9 Агрегаттық (жиынтық ) индекстер Шешімі : 1. Тауар айналымының индексі : 2. Баға индексі :
Слайд 22: Агрегаттық (жиынтық ) индекстер
10 Агрегаттық (жиынтық ) индекстер 3. Сатып алушылардың бағаның өзгеруінен үнемдеуі немесе ұтылуы: 4. Өнімнің физикалық көлемінің агрегаттық индексі : Тексеру :
Слайд 23: Агрегаттық (жиынтық ) индекстер
11 Агрегаттық (жиынтық ) индекстер 4. Өзіндік құнның индексі : Кәсіпорынның өзіндік құнды төмендетуден алатын үнемдеу сомасы :
Слайд 24: Агрегаттық (жиынтық ) индекстер
12 Агрегаттық (жиынтық ) индекстер 5. I шығарылған өнім көлемінің агрегаттық индексі : 6. Өндіріс шығындары индексі :
Слайд 25: Агрегаттық (жиынтық ) индекстер
13 Агрегаттық (жиынтық ) индекстер 7. Еңбек өнімділігінің индексі : 8. Еңбек сыйымдылығының агрегаттық индексі :
Слайд 26: Средние индексы
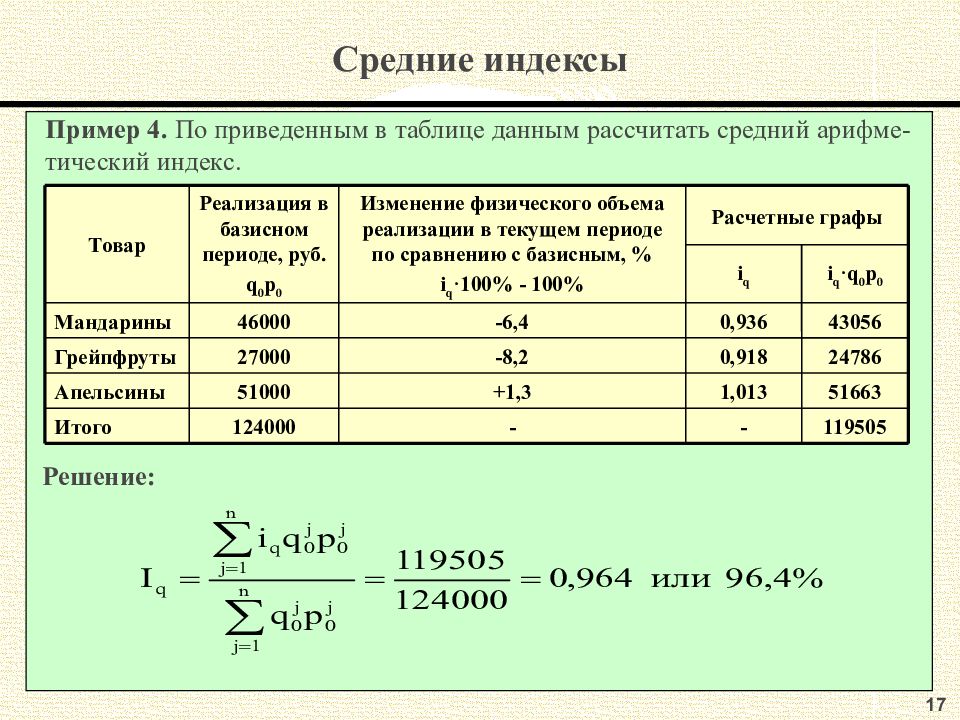
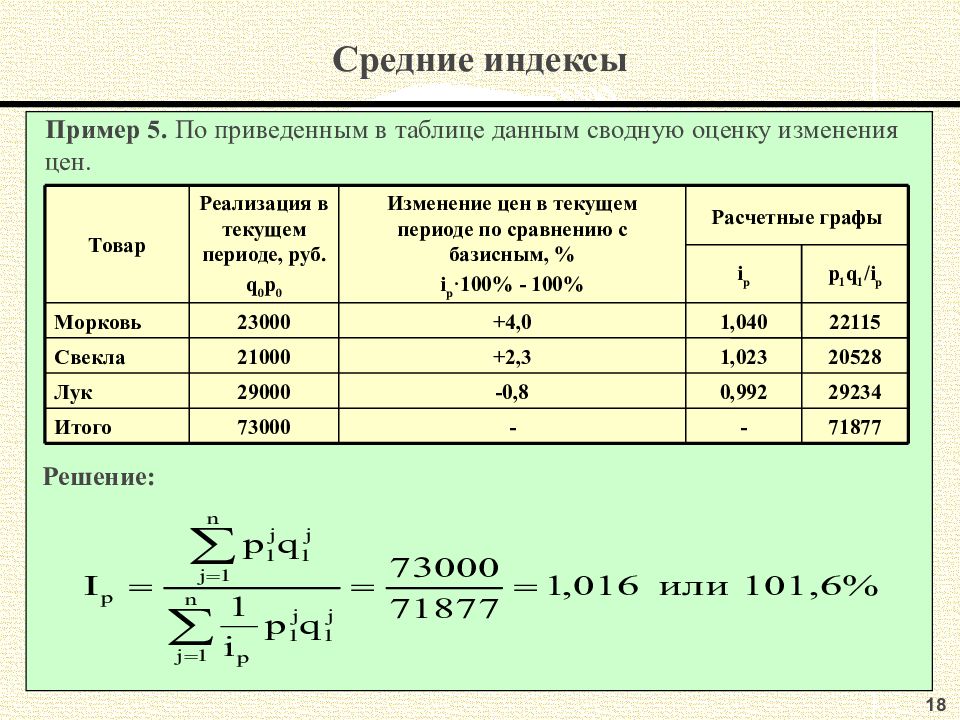
16 Средние индексы 1. Средний арифметический индекс. Получается при помощи преобразо-вания агрегатного индекса физического объема продукции, учитывая что q 1 =i q q 0 : 2. Средний гармонический индекс. Получается при помощи преобразо-вания агрегатного индекса цен, учитывая что p 0 =p 1 /i p :
Слайд 27: Средние индексы
17 Средние индексы Пример 4. По приведенным в таблице данным рассчитать средний арифме-тический индекс. 0,918 -8,2 - 1,013 0,936 119505 - 124000 Итого 51663 +1,3 51000 Апельсины 24786 27000 Грейпфруты 43056 -6,4 46000 Мандарины i q ·q 0 p 0 i q Расчетные графы Изменение физического объема реализации в текущем периоде по сравнению с базисным, % i q · 100% - 100% Реализация в базисном периоде, руб. q 0 p 0 Товар Решение:
Слайд 28: Средние индексы
18 Средние индексы Пример 5. По приведенным в таблице данным сводную оценку изменения цен. 1, 023 +2,3 - 0, 992 1, 040 71877 - 73000 Итого 29234 -0,8 29000 Лук 20528 21000 Свекла 22115 +4,0 23000 Морковь p 1 q 1 /i p i p Расчетные графы Изменение цен в текущем периоде по сравнению с базисным, % i p · 100% - 100% Реализация в текущем периоде, руб. q 0 p 0 Товар Решение:
Слайд 29: Средние индексы
19 Средние индексы 3. Средний арифметический индекс производительности труда по трудоемкости (индекс Струмилина):
Слайд 30: Системы индексов
20 Системы индексов 1. Цепные индексы цен с переменными весами: 2. Цепные индексы цен с постоянными весами:
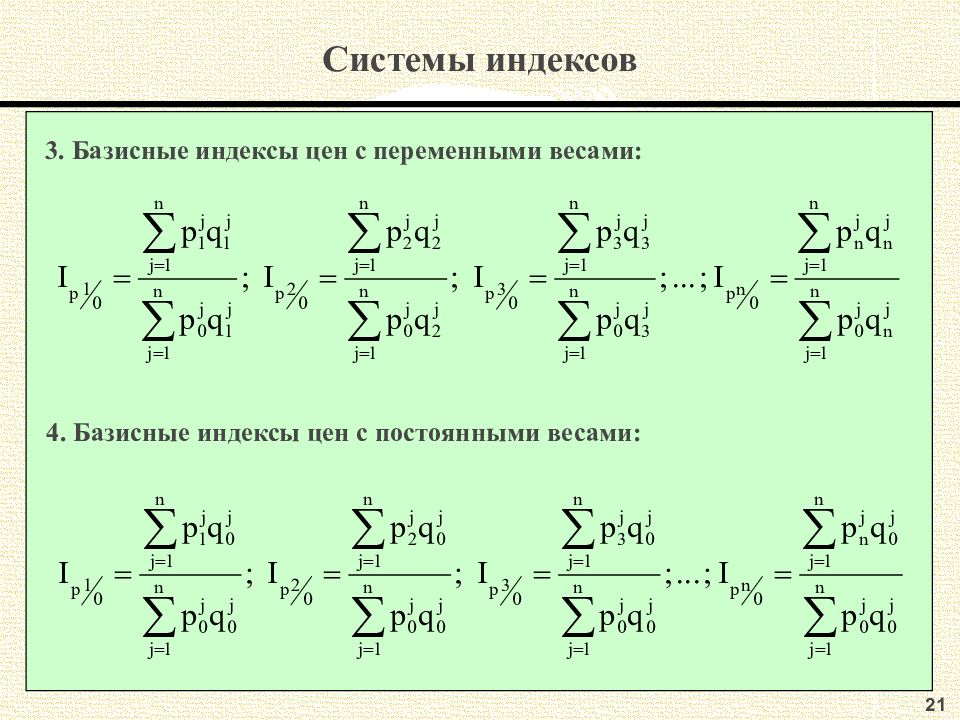
Слайд 31: Системы индексов
21 Системы индексов 3. Базисные индексы цен с переменными весами: 4. Базисные индексы цен с постоянными весами:
Слайд 32: Индексы постоянного и переменного состава
22 Индексы постоянного и переменного состава 1. Индекс переменного состава: 2. Индекс структурных сдвигов:
Слайд 33: Индексы постоянного и переменного состава
2 3 Индексы постоянного и переменного состава 3. Индекс цен фиксированного состава:
Слайд 34: Агрегатные (сводные) индексы
24 Агрегатные (сводные) индексы Пример 6. Имеются следующие данные о реализации товара А в двух регионах: Регион Июнь Июль Расчетные графы, руб. цена за шт., руб. p 0 продано шт., q 0 цена за шт., руб. p 1 продано шт., q 1 p 0 q 0 p 1 q 1 p 0 q 1 1 12 10000 13 18000 120000 234000 216000 2 17 20000 19 9000 340000 171000 153000 Итого - 30000 - 27000 460000 405000 369000 Провести анализ изменения цен реализации товара.
Слайд 35: Индексы постоянного и переменного состава
25 Индексы постоянного и переменного состава 1. Индекс цен переменного состава: 2. Индекс структурных сдвигов:
Слайд 36: Индексы постоянного и переменного состава
26 Индексы постоянного и переменного состава 3. Индекс цен фиксированного состава:
Слайд 37: Территориальные индексы
2 7 Территориальные индексы Территориальные индексы служат для сравнения показателей в пространстве, т.е. по предприятиям, округам, городам, районам, республикам, странам и пр. Способы расчета территориальных индексов. 1. В качестве весов принимается сумма объемов проданных товаров по двум регионам: Территориальный индекс цен:
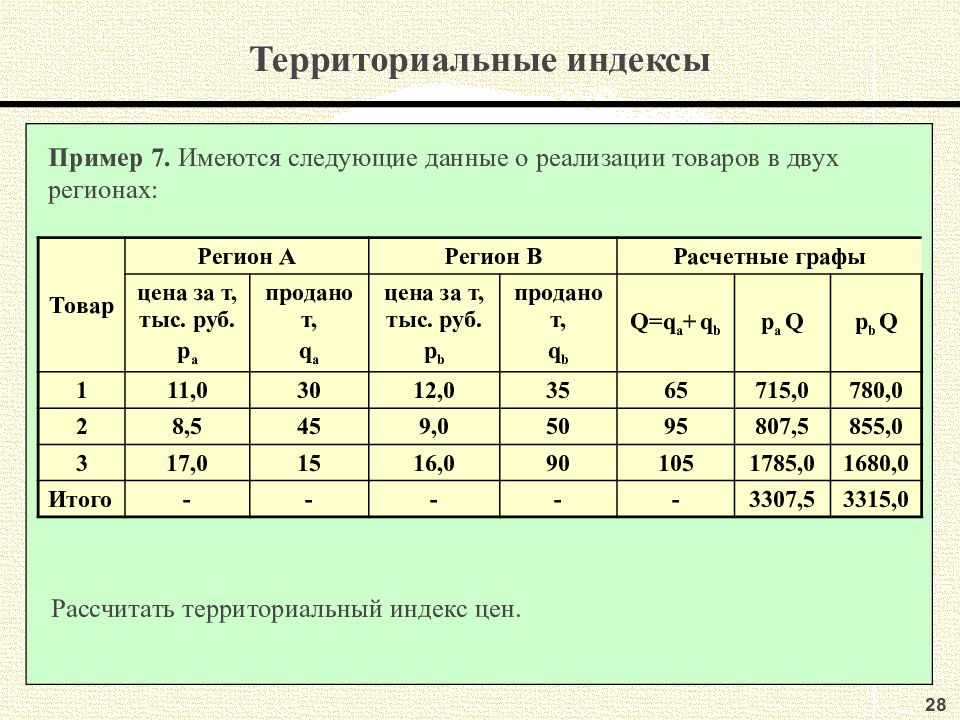
Слайд 38: Территориальные индексы
2 8 Территориальные индексы Пример 7. Имеются следующие данные о реализации товаров в двух регионах: Товар Регион А Регион В Расчетные графы цена за т, тыс. руб. p а продано т, q a цена за т, тыс. руб. p b продано т, q b Q=q a + q b p a Q p b Q 1 1 1,0 30 1 2,0 35 65 715,0 780,0 2 8,5 45 9,0 50 95 807,5 855,0 3 17,0 15 16,0 90 105 1785,0 1680,0 Итого - - - - - 3307,5 3315,0 Рассчитать территориальный индекс цен.
Слайд 39: Территориальные индексы
2 9 Территориальные индексы Территориальный индекс цен: или
Слайд 40: Территориальные индексы
30 Территориальные индексы Территориальный индекс цен: 2. Учитывается соотношение весов сравниваемых территорий.
Слайд 41: Территориальные индексы
31 Территориальные индексы Территориальный индекс физического объема реализации: Территориальный индекс товарооборота: