Первый слайд презентации: Электротехника, электроника и схемотехника
Часть 1. Электротехника. Раздел 1. Электрические цепи постоянного тока Классификация методов расчета. Свойства цепей Универсальные методы расчета электрических цепей Расчет электрических цепей для частных случаев
Слайд 2: Классификация методов расчета линейных электрических цепей (постоянного и переменного тока)
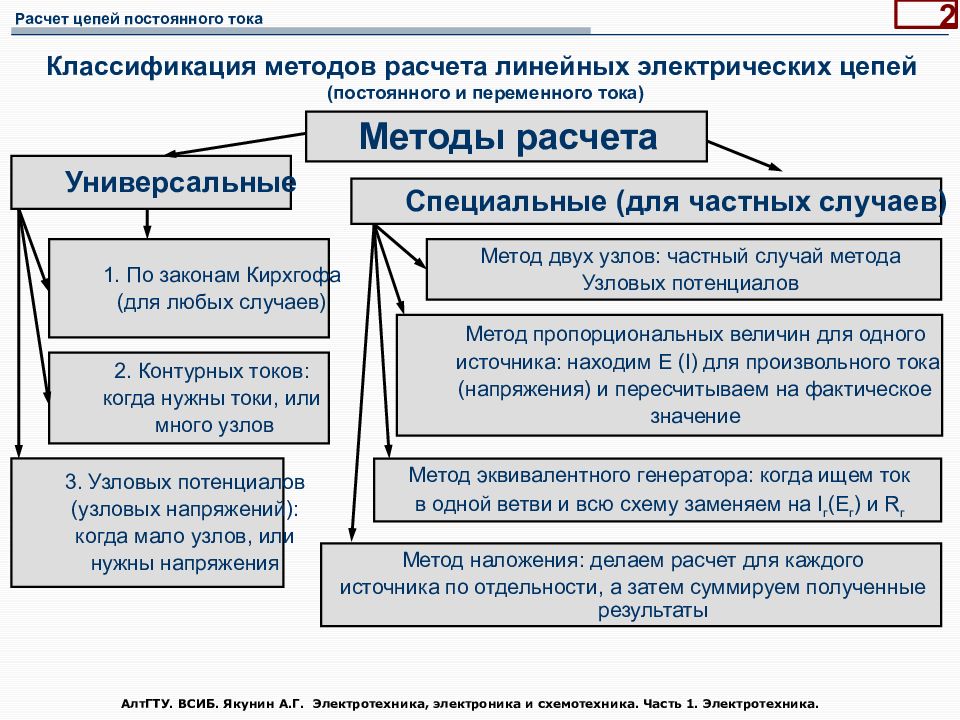
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 2 Классификация методов расчета линейных электрических цепей (постоянного и переменного тока) Методы расчета Универсальные Специальные (для частных случаев) 1. По законам Кирхгофа (для любых случаев) Метод пропорциональных величин для одного источника: находим E ( I) для произвольного тока (напряжения) и пересчитываем на фактическое значение Метод эквивалентного генератора: когда ищем ток в одной ветви и всю схему заменяем на I г (E г ) и R г Метод двух узлов: частный случай метода Узловых потенциалов 2. Контурных токов: когда нужны токи, или много узлов 3. Узловых потенциалов (узловых напряжений): когда мало узлов, или нужны напряжения Метод наложения: делаем расчет для каждого источника по отдельности, а затем суммируем полученные результаты
Слайд 3: Потенциальная диаграмма и энергетический баланс
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 3 Потенциальная диаграмма и энергетический баланс Потенциальная диаграмма - график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек Баланс мощностей - следствие закона сохранения энергии и может служить критерием правильности расчета электрической цепи: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи. Если направление тока противоположно ЭДС, мощность на источнике будет отрицательной Задача о максимальном к.п.д. – при каком соотношении между R н и R г к.п.д. максимален? Задача о максимальной мощности – при каком соотношении между R н и R г мощность на нагрузке максимальна? Передача энергии на расстояние – почему для передачи электроэнергии используют высокое напряжение?
Слайд 4: Свойства и понятия линейных цепей
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 4 Свойства и понятия линейных цепей Определение: линейной называют цепь, для всех элементов которой соблюдается закон Ома. В ней всегда соблюдаются зависимости y=ax+b, где х – ток или напряжение в одной ветви, а y – в другой Принцип наложения (суперпозиции): ток в k – й ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности Принцип (теорема) взаимности: если ЭДС, действуя в некоторой ветви схемы, не содержащей других источников, вызывает в другой ветви ток, то перенесенная в эту ветвь ЭДС вызовет в первой ветви такой же ток. Входная проводимость Y ii или g ii : проводимость, равная отношению тока к ветви к ЭДС источника, установленного в эту ветвь (проводимость между двумя точками цепи) Взаимная проводимость Y ik или g ik : проводимость, равная отношению тока в m- й ветви к ЭДС источника, установленного в k- ю ветвь Аналогичным образом определяются входные и взаимные сопротивления ветвей R ki =1/Y ki и коэффициенты передачи токов k ki =I i /I k и напряжений h ki =U i /U k Теорема вариаций: вариации токов, ЭДС, напряжений и сопротивлений линейно связаны между собой Вариации ЭДС и токов: ΔI k = Sum ( ΔE m * g km )+ Sum ( ΔJ j * k k m ); Δ U k = Sum ( ΔE m * h km )+ Sum ( ΔJ m * R k m ) Вариации ЭДС сопротивлений: ΔI k =-( g m k * ΔR k *I m )/(1+ ΔR k *g mm ) ; ΔI m =-( g m m * ΔR k *I m )/(1+ ΔRk *g mm ) Теорема компенсации: вместо сопротивления можно включить ЭДС = падению напряжения на нем. Теорема вариаций Теорема компенсации
Слайд 5: Пример решения задачи по законам Кирхгофа
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 5 Пример решения задачи по законам Кирхгофа Дано: R1=16 Ом; R2=31 Ом; R3=24 Ом;R4=13 Ом; R5=33 Ом; R6=40 Ом; R7=22 Ом; R8=7 Ом; E1=30 В; E2=24 В; E7=16 В; E8=11 В. Найти: Токи в цепи Решение В приведенной схеме m=7 ветвей и n=4 узла. 1. Подсчитываем число уравнений по законам Кирхгофа. Первый закон Кирхгофа ( n-1 =3 уравнения): сумма втекающих и вытекающих токов в любом узле схемы равна нулю Второй закон Кирхгофа ( m-(n+1) = 4 уравнения): алгебраическая сумма падений напряжений по замкнутому контуру равна сумме ЭДС в этом контуре. 2. Размечаем произвольно выбранные направления токов, контуры обходов, узлы схемы 3. Ответ: I1=0,265 А; I2=0,082 А; I3=0,347 А; I5=0,131 А; I6=0,214 А; I7=0,140 А; I8=-0,273 А. http://toe5.ru/examples.php 3. Составляем уравнения по законам Кирхгофа, подставляем значения и находим решение
Слайд 6: Метод контурных токов
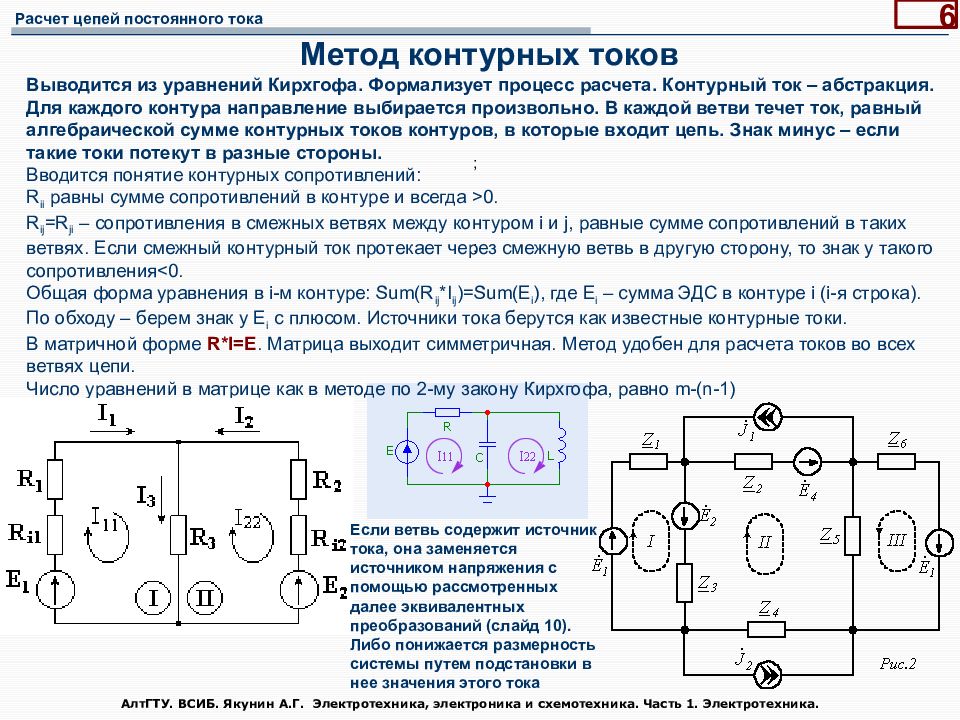
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 6 Метод контурных токов ; ; ; ; Выводится из уравнений Кирхгофа. Формализует процесс расчета. Контурный ток – абстракция. Для каждого контура направление выбирается произвольно. В каждой ветви течет ток, равный алгебраической сумме контурных токов контуров, в которые входит цепь. Знак минус – если такие токи потекут в разные стороны. Вводится понятие контурных сопротивлений: R ii равны сумме сопротивлений в контуре и всегда >0. R i j = R ji – сопротивления в смежных ветвях между контуром i и j, равные сумме сопротивлений в таких ветвях. Если смежный контурный ток протекает через смежную ветвь в другую сторону, то знак у такого сопротивления<0. Общая форма уравнения в i-м контуре: Sum ( R ij * I ij )= Sum ( E i ), где E i – сумма ЭДС в контуре i (i-я строка). По обходу – берем знак у E i с плюсом. Источники тока берутся как известные контурные токи. В матричной форме R*I=E. Матрица выходит симметричная. Метод удобен для расчета токов во всех ветвях цепи. Число уравнений в матрице как в методе по 2-му закону Кирхгофа, равно m - (n-1) Если ветвь содержит источник тока, она заменяется источником напряжения с помощью рассмотренных далее эквивалентных преобразований ( слайд 10). Либо понижается размерность системы путем подстановки в нее значения этого тока
Слайд 7: Пример решения задачи методом контурных токов (МКТ)
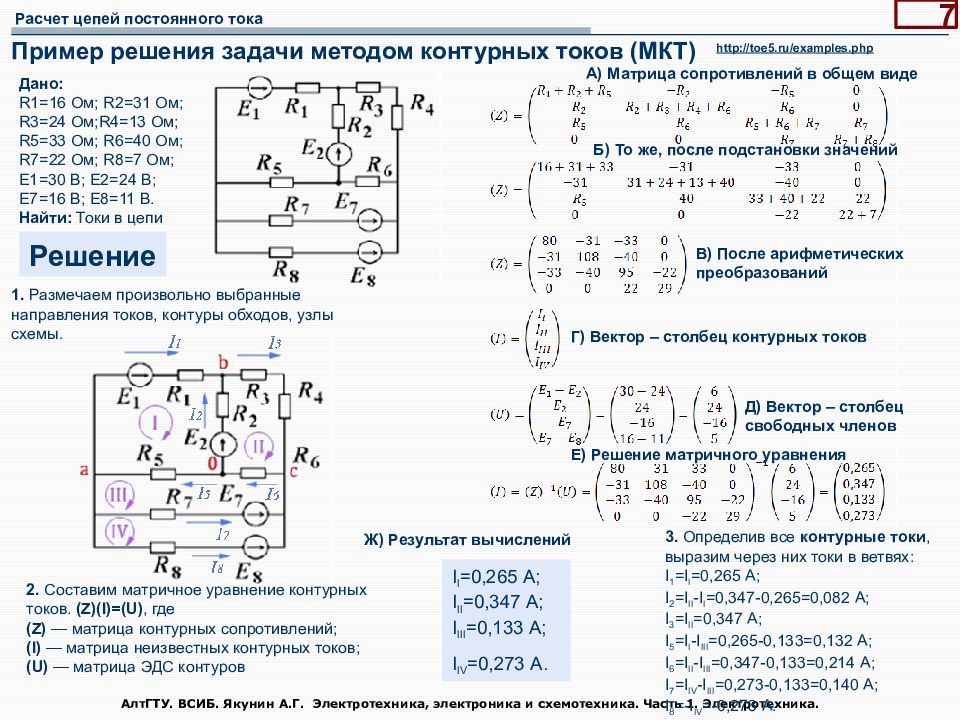
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 7 Пример решения задачи методом контурных токов (МКТ) Дано: R1=16 Ом; R2=31 Ом; R3=24 Ом;R4=13 Ом; R5=33 Ом; R6=40 Ом; R7=22 Ом; R8=7 Ом; E1=30 В; E2=24 В; E7=16 В; E8=11 В. Найти: Токи в цепи Решение 1. Размечаем произвольно выбранные направления токов, контуры обходов, узлы схемы. 2. Составим матричное уравнение контурных токов. (Z)(I)=(U), где (Z) — матрица контурных сопротивлений; (I) — матрица неизвестных контурных токов; (U) — матрица ЭДС контуров 3. Определив все контурные токи, выразим через них токи в ветвях: I 1 =I I =0,265 А; I 2 =I II -I I =0,347-0,265=0,082 А; I 3 =I II =0,347 А; I 5 =I I -I III =0,265-0,133=0,132 А; I 6 =I II -I III =0,347-0,133=0,214 А; I 7 =I IV -I III =0,273-0,133=0,140 А; I 8 =-I IV =-0,273 А. I I =0,265 А; I II =0,347 А; I III =0,133 А; I IV =0,273 А. А) Матрица сопротивлений в общем виде Б) То же, после подстановки значений В) После арифметических преобразований Г) Вектор – столбец контурных токов Д) Вектор – столбец свободных членов Е) Решение матричного уравнения Ж) Результат вычислений http://toe5.ru/examples.php
Слайд 8: Метод узловых потенциалов (узловых напряжений)
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 8 Метод узловых потенциалов (узловых напряжений) Вытекает из законов Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно числу ветвей дерева Введем понятия: 1. Проводимость i- го узла g i – сумма проводимостей всех присоединенных к нему ветвей. 2. Узловой ток I i – сумма ЭДС во всех присоединенных к i-му узлу ветвях, поделенная на сопротивление этих ветвей, то есть I i = Σ ( Ej * g j ), где суммирование ведется по всем смежным с узлом ветвям j, g j – суммарная эквивалентная проводимость j –й ветви, а E j – ее суммарная эквивалентная э.д.с.. Знак э.д.с. >0, если она направлена к узлу. 3. Проводимость ветви между узлами i и j: g ij =1/ R ij. Тогда для каждого узла i составляем линейное уравнение вида: g i * i - Σ (g ij * i )= I i. Число таких уравнений = число узлов -1. Как и для метода контурных токов, система уравнений может быть записана в матричной форме http://toe5.ru/examples.php Если ветвь ij, между узлами i и j содержит только ЭДС E ij, то для таких ветвей j-e уравнение из системы исключается, а вместо потенциала φ j в другие уравнения подставляется величина φ i + E ij. Альтернативный вариант – заменить эту ветвь с помощью приведенных далее эквивалентных преобразований (слайд10)
Слайд 9: Пример решения задачи методом узловых потенциалов
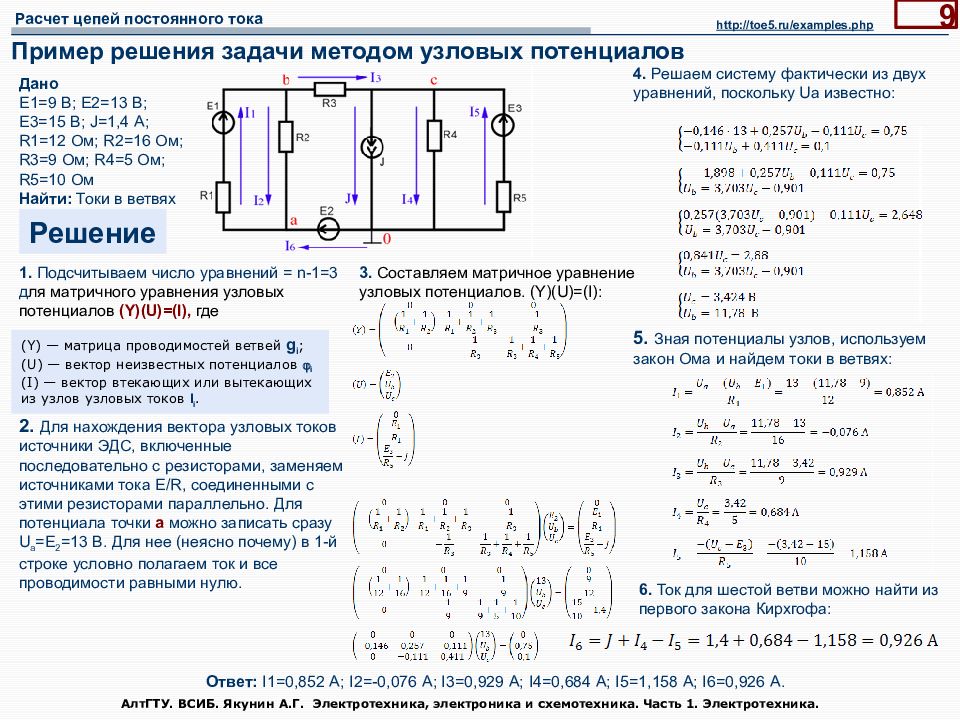
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 9 Пример решения задачи методом узловых потенциалов Дано Е1=9 В; Е2=13 В; Е3=15 В; J=1,4 А; R1=12 Ом; R2=16 Ом; R3=9 Ом; R4=5 Ом; R5=10 Ом Найти: Токи в ветвях Решение 1. Подсчитываем число уравнений = n-1=3 д ля матричного уравнения узловых потенциалов (Y)(U)=(I), где 2. Для нахождения вектора узловых токов источники ЭДС, включенные последовательно с резисторами, заменяем источниками тока E/R, соединенными с этими резисторами параллельно. Для потенциала точки a можно записать сразу U a =E 2 =13 В. Для нее (неясно почему) в 1-й строке условно полагаем ток и все проводимости равными нулю. 6. Ток для шестой ветви можно найти из первого закона Кирхгофа: Ответ: I1=0,852 А; I2=-0,076 А; I3=0,929 А; I4=0,684 А; I5=1,158 А; I6=0,926 А. http://toe5.ru/examples.php 5. Зная потенциалы узлов, используем закон Ома и найдем токи в ветвях: (Y) — матрица проводимостей ветвей g i ; (U) — вектор неизвестных потенциалов i (I) — вектор втекающих или вытекающих из узлов узловых токов I i. 3. Составляем матричное уравнение узловых потенциалов. (Y)(U)=(I): 4. Решаем систему фактически из двух уравнений, поскольку Ua известно:
Слайд 10: Эквивалентные преобразования
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 10 Эквивалентные преобразования 1. Замена последовательных или параллельных соединений нескольких однотипных элементов одним 2. Взаимные преобразования звезды и треугольника. ; ; ; ; g 1 =1/ R 1 ; g 2 =1/ R 2 ; g 3 =1/ R 3 ; g 12 =1/ R 12 ; g 23 =1/ R 23 ; g 31 =1/ R 31. 3. Замена параллельных ветвей с R k, E k, J k на одну ветвь с последовательно включенными эквивалентной проводимостью g экв = Σ (g k ) и эквивалентным источником ЭДС E экв ={ Σ (E k *g k )+ Σ ( J k )}/ g экв. Приведенные формулы могут легко быть выведены из метода узловых потенциалов. 4. Перенос источников ЭДС из ветви в два узла: Снимает проблему появления бесконечной проводимости ветвей, содержащих только ЭДС, в методе узловых потенциалов 5. Перенос источника тока из ветви контура в другие ветви с удалением исходной ветви. Дальнейшее преобразование – замена каждой параллельной цепочки из источника тока и сопротивления эквивалентным источником напряжения с последовательно включенным сопротивлением. 6. Преобразование реального источника тока в реальный источник напряжения и наоборот. 7. Замена произвольного сопротивления в цепи источником ЭДС по теореме компенсации
Слайд 11: Метод двух узлов
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 11 Метод двух узлов В данном методе система уравнений вырождается в уравнение для одного узла вида: g · = I, где I = Σ J + Σ (E i ·g i ) - узловой ток; g= Σ g i - узловая проводимость; g i =1/ R i – проводимость i- й ветви, содержащей сопротивление R i и, возможно, ЭДС E i, но не содержащей источник тока J i - ток в ветви, содержащей источник тока Отсюда получаем развернутое выражение для искомого потенциала: = ( Σ J + Σ (E i ·g i ) ) / Σ g i http://toe5.ru/examples.php Метод двух узлов – это метод расчета электрических цепей, в котором неизвестной величиной является напряжение между двумя узлами электрической цепи, причем вся цепь состоит только из двух узлов. Является частным случаем метода узловых потенциалов, когда число узлов равно двум и фактически сводится к эквивалентному преобразованию 3 на предыдущем слайде Пример расчета для приведенной на рисунке схемы: а = ( E 1 /R 1 -E 2 /R 2 )/(1/R 1 +1/R 2 +1/R 3 +1/R 4 ) Тогда I 1 =( а - E 1 )/R 1, I 2 = а /R 2, I 1 =( а + E 2 )/R 1, I 4 = а /R 4,
Слайд 12: Метод эквивалентного генератора (МЭГ)
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 12 Метод эквивалентного генератора (МЭГ) По теореме об эквивалентном генераторе ток в нагрузке можно найти по формуле: http://toe5.ru/examples.php Используется при определении тока или падения напряжения на одной ветви или на одном компоненте. При этом сколько угодно сложная схема приводится к простейшей эквивалентной схеме, которая содержит идеальный источник э.д.с. Е и внутренний резистор с сопротивлением R в Uхх — напряжение холостого хода генератора; Rн — сопротивление нагрузки; Rг — сопротивление генератора относительно зажимов нагрузки. Применяется, когда интерес представляет нахождение тока и/или напряжения на отдельном элементе цепи Rk. Вся схема при этом заменяется активным двухполюсником представляющим собой некоторый эквивалентный генератор, параметры которого надо изначально определить. Порядок расчета. 1. Находим напряжение холостого хода U хх, для чего исключаем из цепи интересуемый элемент R k и рассчитываем величину напряжения на зажимах цепи, к которым он должен подключаться. 2. Находим входное сопротивление исследуемой цепи относительно клемм интересуемого элемента, например, методом эквивалентных преобразований, исключив из схемы все источники тока и напряжения. Найденное значение будет равно внутреннему сопротивлению эквивалентного генератора R ген. Возможен альтернативный вариант, когда находится ток в цепи I кз с закороченным элементом R k, а затем находим R ген по формуле R ген = U хх / I кз. 3. Искомые параметры цепи определим из выражений I k =U хх /(R ген +R k ); U k =I k *R, где R k – величина сопротивления, на котором ищется ток и/или напряжение. На практике метод часто применяется в модифицированном виде для нахождения токов и/или напряжений на участке цепи для произвольно заданного значения некоторого элемента. Для этого сначала измеряется напряжение на выводах схемы при отключенном элементе, равное U хх. Затем измеряется напряжение U o, когда к выводам подключено известное сопротивление R o и находится R ген = R o (U хх - U o )/ U o. Если R ген достаточно велико, его величину можно более точно определить путем измерения тока короткого замыкания по вышеописанной в п.2 формуле.
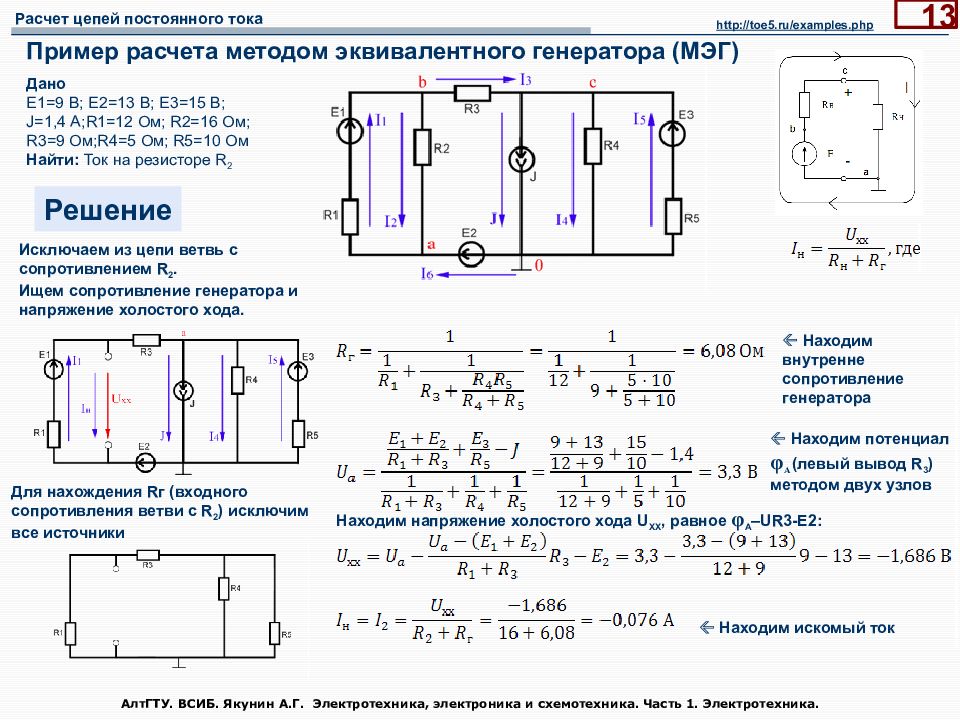
Слайд 13: Пример расчета методом эквивалентного генератора (МЭГ)
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 13 Пример расчета методом эквивалентного генератора (МЭГ) Дано Е1=9 В; Е2=13 В; Е3=15 В; J=1,4 А;R1=12 Ом; R2=16 Ом; R3=9 Ом;R4=5 Ом; R5=10 Ом Найти: Ток на резисторе R 2 Решение http://toe5.ru/examples.php Для нахождения R г (входного сопротивления ветви с R 2 ) исключим все источники Исключаем из цепи ветвь с сопротивлением R 2. Ищем сопротивление генератора и напряжение холостого хода. Находим внутренне сопротивление генератора Находим потенциал φ A (левый вывод R 3 ) методом двух узлов Находим искомый ток Находим напряжение холостого хода U XX, равное φ A – UR3-E2:
Слайд 14: Метод пропорциональных величин
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 14 Метод пропорциональных величин Используется в случаях, когда цепь содержит всего один источник тока или напряжения. Метод особенно удобен, если нужно найти ток и/или напряжение всего на одном элементе цепи. Суть метода заключается в следующем. - На интересуемом элементе задаемся произвольным значением тока и/или напряжения (удобно использовать целые значения, близкие к ожидаемой величине, например, 1 ма, 10 мА, 1 В, 100 В и т.д.) - Выполняется расчет токов и падений напряжений на всех элементах цепи, либо только тех, через которые можно рассчитать величину действующего в цепи значения источника тока или ЭДС. - Определяем коэффициент пропорциональности k, равный отношению заданного значения величины напряжения (тока) источника напряжения (тока) к ее расчетному значению. - Находим значение тока (напряжения) на интересуемом элементе цепи путем умножения изначально установленного значения (или значения, полученного в процессе расчета) на величину k. ; ; Пример применения метода для полного расчета цепи Пусть R1=4 Ом, R2=2 Ом, R3=8 Ом и E= 14 В. 1. Для расчёта выберем самую удалённую от источника ветвь, например с резистором R3. 2. Зададимся для этой ветви произвольным током, например, током I3= 1 А. 3. Для заданного тока найдем токи и напряжения на интересующих участках цепи. Так, по закону Ома UR3= I3p ·R3=8 В, а ток через R2 будет равен I2=UR3/R2=4A. Тогда по первому закону Кирхгофа ток через R1 будет равен I1=I3+I2=5A. Отсюда UR1=I1·R1= 5 А *4 Ом=20В и по второму закону Кирхгофа получим, что расчетное значение ЭДС окажется равным E р= UR2+UR1= 8В+20В=28В. 4. Находим коэффициент пропорциональности, равный отношению k=E / E р = 14В/28В=0.5 5. Находим искомые значения напряжений и токов цепи путем умножения ранее рассчитанных значений на данный коэффициент, например, U1’=U1·k=20 В · 0.5=10В, I3=1A·k=1A· 0.5=0.5A и т.д.
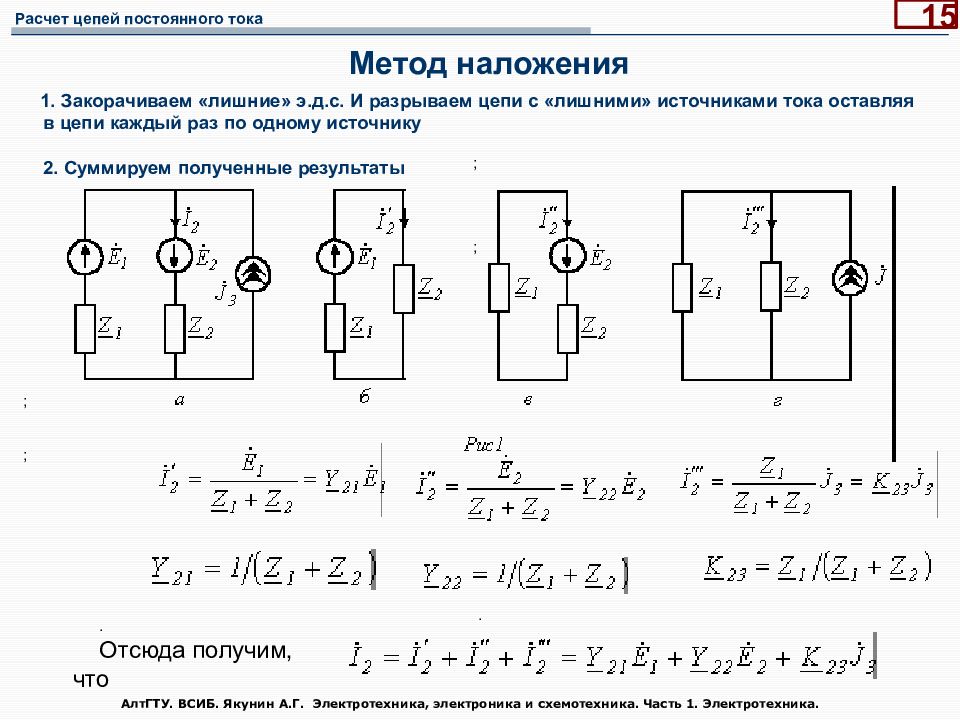
Слайд 15: Метод наложения
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 15 Метод наложения 1. Закорачиваем «лишние» э.д.с. И разрываем цепи с «лишними» источниками тока оставляя в цепи каждый раз по одному источнику 2. Суммируем полученные результаты ; ; ; ; . Отсюда получим, что .
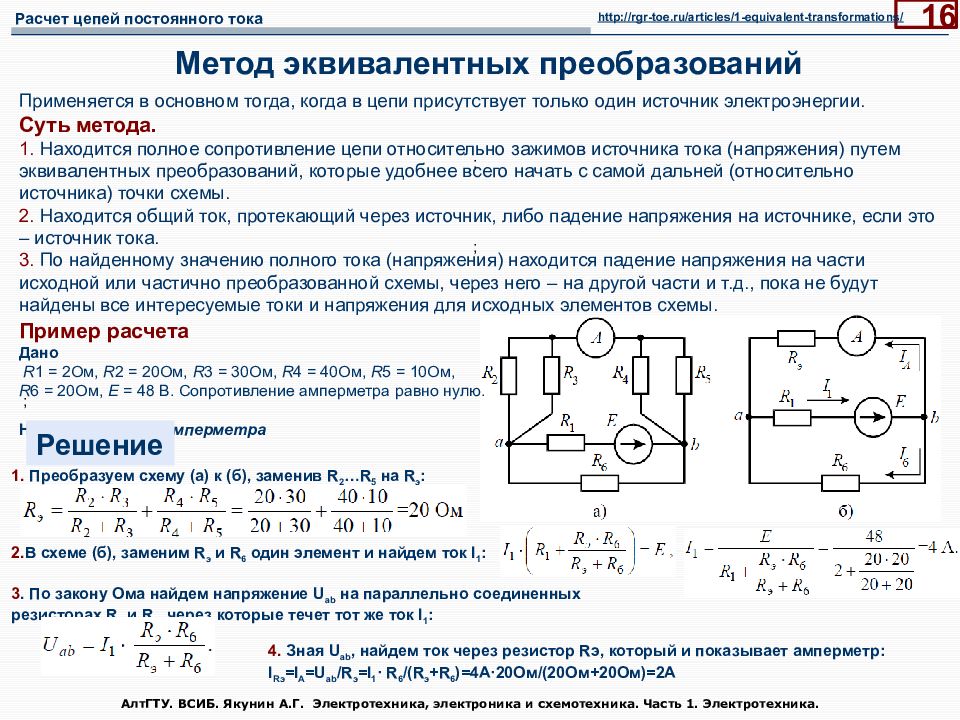
Последний слайд презентации: Электротехника, электроника и схемотехника: Метод эквивалентных преобразований
АлтГТУ. ВСИБ. Якунин А.Г. Электротехника, электроника и схемотехника. Часть 1. Электротехника. 16 Метод эквивалентных преобразований ; ; ; Применяется в основном тогда, когда в цепи присутствует только один источник электроэнергии. Суть метода. 1. Находится полное сопротивление цепи относительно зажимов источника тока (напряжения) путем эквивалентных преобразований, которые удобнее всего начать с самой дальней (относительно источника) точки схемы. 2. Находится общий ток, протекающий через источник, либо падение напряжения на источнике, если это – источник тока. 3. По найденному значению полного тока (напряжения) находится падение напряжения на части исходной или частично преобразованной схемы, через него – на другой части и т.д., пока не будут найдены все интересуемые токи и напряжения для исходных элементов схемы. http://rgr-toe.ru/articles/1-equivalent-transformations/ Пример расчета Дано R 1 = 2Ом, R 2 = 20Ом, R 3 = 30Ом, R 4 = 40Ом, R 5 = 10Ом, R 6 = 20Ом, E = 48 В. Сопротивление амперметра равно нулю. Найти: показания амперметра Решение 1. Преобразуем схему (а) к (б), заменив R 2 …R 5 на R э : 2. В схеме (б), заменим R э и R 6 один элемент и найдем ток I 1 : 3. По закону Ома найдем напряжение U ab на параллельно соединенных резисторах R э и R 6, через которые течет тот же ток I 1 : 4. Зная U ab, найдем ток через резистор R э, который и показывает амперметр: I R э = I A =U ab /R э = I 1 · R 6 /(R э + R 6 )=4A·20 Ом/(20Ом+20Ом)=2А