Первый слайд презентации
ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ Презентация к уроку по информатике в 8 классе Подготовила: Гвозденко Ольга Викторовна Учитель информатики МКОУ Марченковская ООШ
Слайд 2
Логика – наука, изучающая законы и формы мышления Этапы развития логики: 1 этап – формальная логика. Основатель Аристотель (384-322 гг до н.э.), ввел основные формы абстрактного мышления. 2 этап – математическая логика. Основатель – немецкий ученый и философ Лейбниц (1642-1716гг), предпринял попытку логических вычислений. 3 этап – математическая логика (булева алгебра). Основатель английский математик Джорж Буль (1815-1864гг), ввел алфавит, орфографию и грамматику математической логики.
Слайд 3
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Логическое высказывание – это любое повествовательное предложение в отношении которого можно однозначно сказать, истинно оно или ложно. Пример: 6- четное число – истина Рим – столица Франции – ложно Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Истинному высказыванию ставится в соответствие 1, ложному — 0. Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна. Таблица истинности – таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функций.
Слайд 4
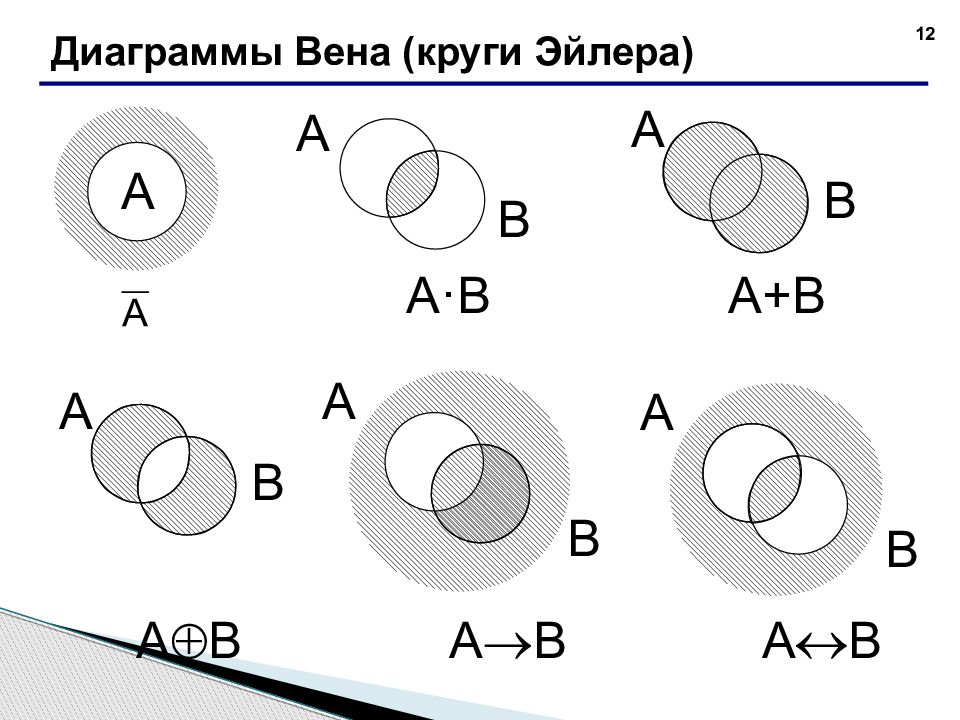
Логическая операция КОНЪЮНКЦИЯ (логическое умножение) : в естественном языке соответствует союзу и ; в алгебре высказываний обозначение & ; в языках программирования обозначение A nd. Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам. Таблица истинности Диаграмма Эйлера-Венна А В А & В 0 0 0 0 1 0 1 0 0 1 1 1
Слайд 5
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение) : - в естественном языке соответствует союзу или ; - обозначение V ; в языках программирования обозначение O r. Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В. Таблица истинности Диаграмма Эйлера-Венна А В А Ú В 0 0 0 0 1 1 1 0 1 1 1 1
Слайд 6
Логическая операция ИНВЕРСИЯ (отрицание) : в естественном языке соответствует словам неверно, что... и частице не - обозначение A в языках программирования обозначение N ot ; Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества. Таблица истинности Диаграмма Эйлера-Венна A _ A 0 1 1 0
Слайд 7
Логическая операция ИМПЛИКАЦИЯ (логическое следование) : - в естественном языке соответствует обороту если..., то... ; обозначение == >. Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно А В А Þ В 0 0 1 0 1 1 1 0 0 1 1 1 Если на улице дождь, то асфальт мокрый Если число делится на 9, то оно делиться на 3
Слайд 8
Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность) : - в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае ; - обозначения <==>. Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции : А В А Û В 0 0 1 0 1 0 1 0 0 1 1 1 Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, V, ==>, <==>. Число кратно 3 тогда и только тогда, когда сумма его цифр делится нацело на 3
Слайд 9
логические выражения и таблицы истинности Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания. Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности. Алгоритм построения таблицы истинности: 1.подсчитать количество переменных n в логическом выражении; 2.определить число строк в таблице, которое равно m = 2n; 3.подсчитать количество логических операций в логическом выражении и 4.определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций; 5.ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов; 6.заполнить столбцы входных переменных наборами значений; 7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Слайд 10
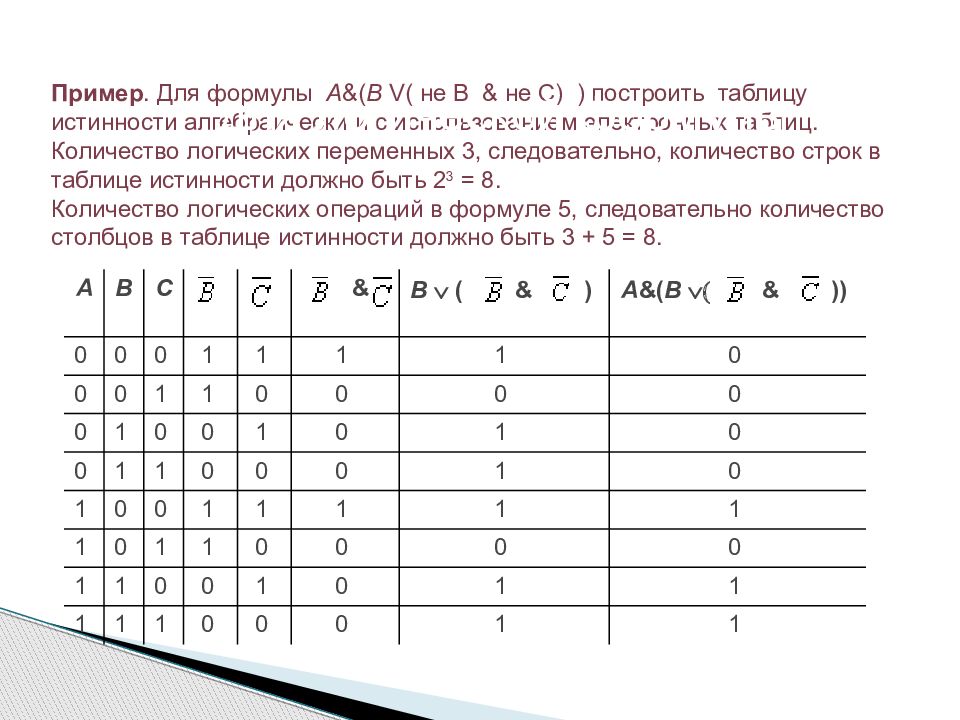
Пример. Для формулы A &( B V ( не В & не С) ) построить таблицу истинности алгебраически и с использованием электронных таблиц. Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2 3 = 8. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8. A B C & B Ú ( & ) A &( B Ú( & ) ) 0 0 0 1 1 1 1 0 0 0 1 1 0 0 0 0 0 1 0 0 1 0 1 0 0 1 1 0 0 0 1 0 1 0 0 1 1 1 1 1 1 0 1 1 0 0 0 0 1 1 0 0 1 0 1 1 1 1 1 0 0 0 1 1 Составление таблиц истинности для логической формулы
Слайд 11
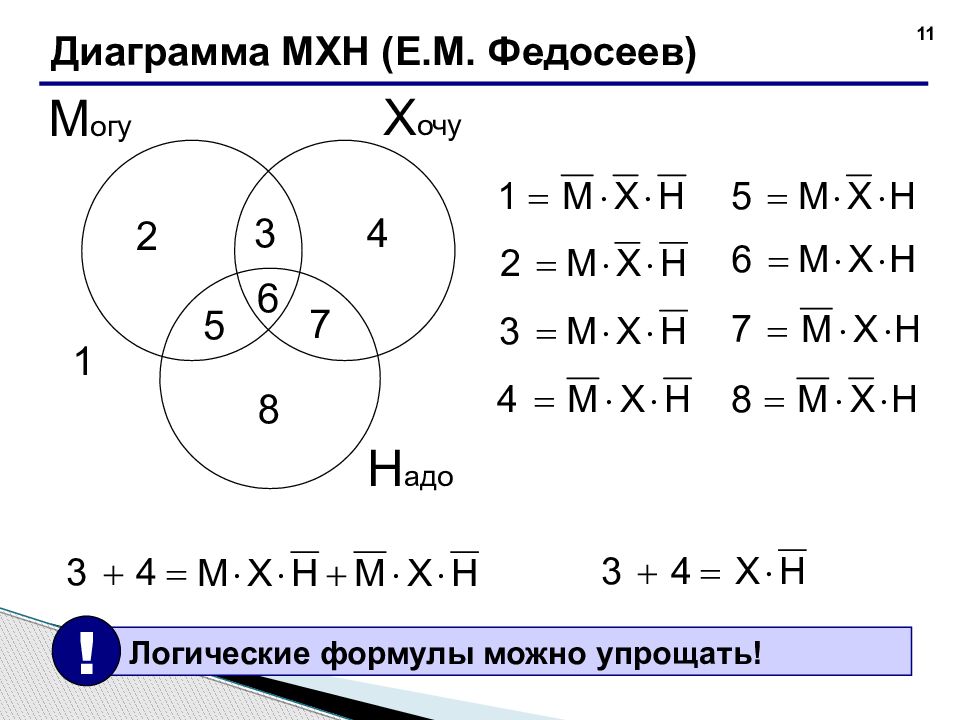
11 Диаграмма МХН (Е.М. Федосеев) Х очу М огу Н адо 1 2 3 4 5 6 7 8 Логические формулы можно упрощать! !