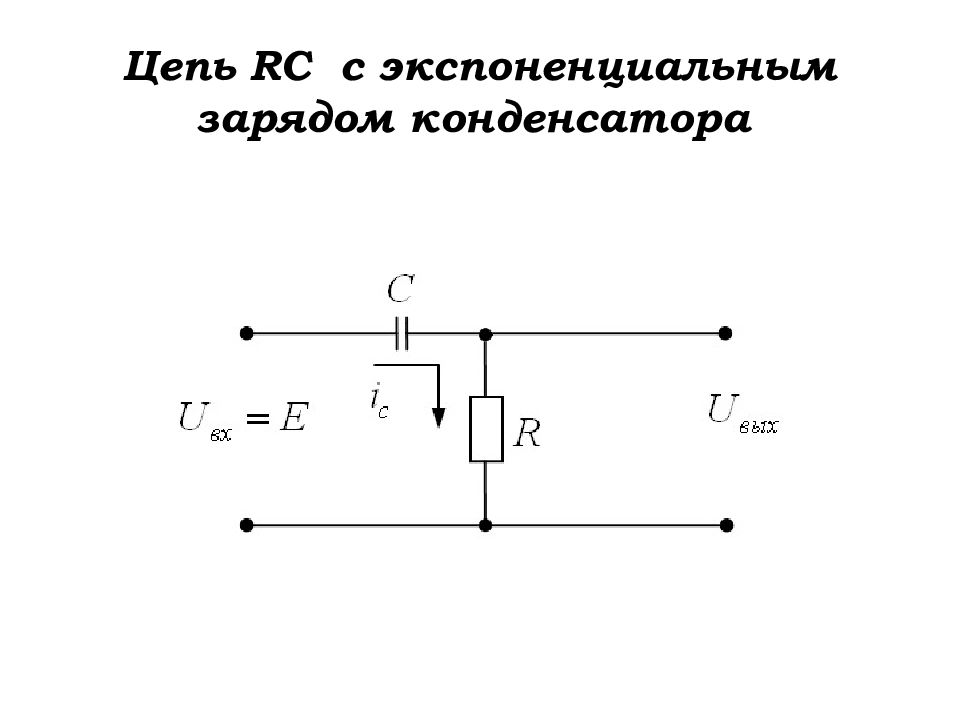
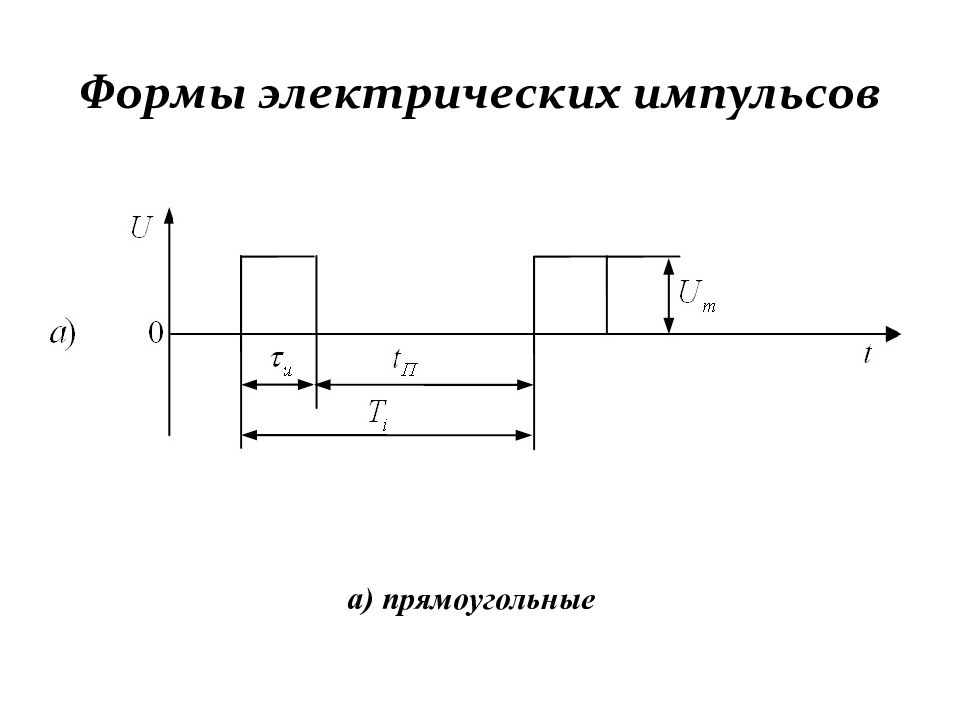
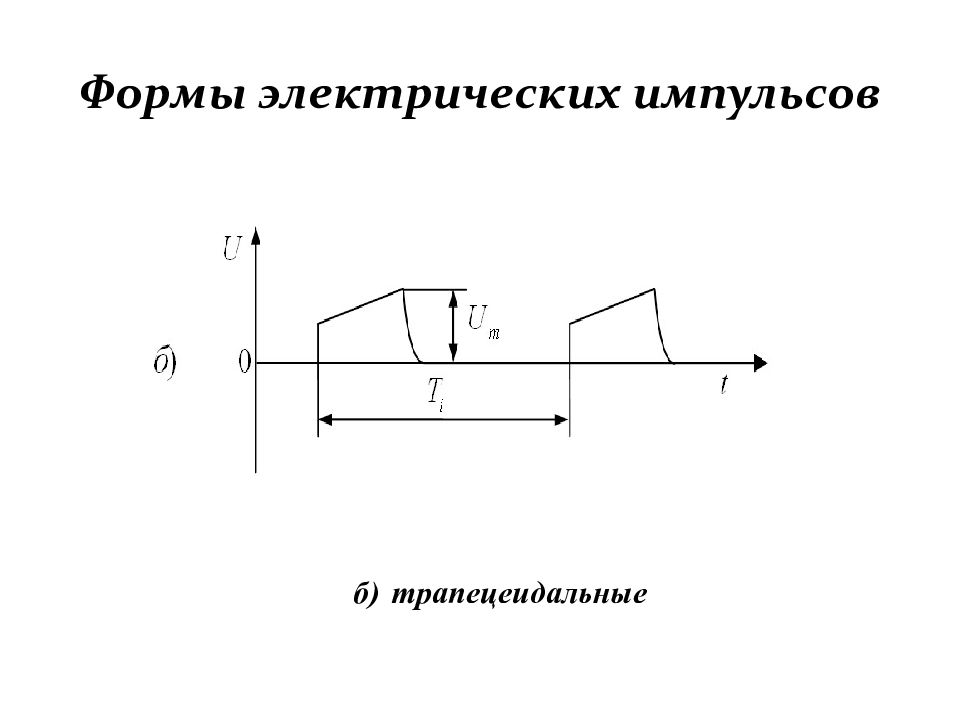
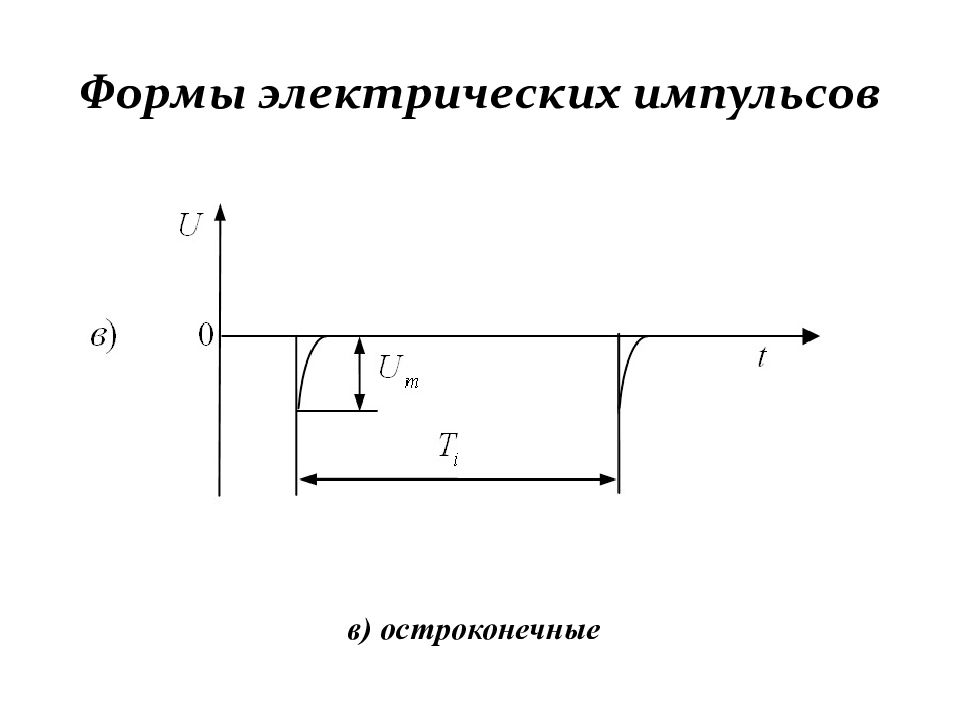
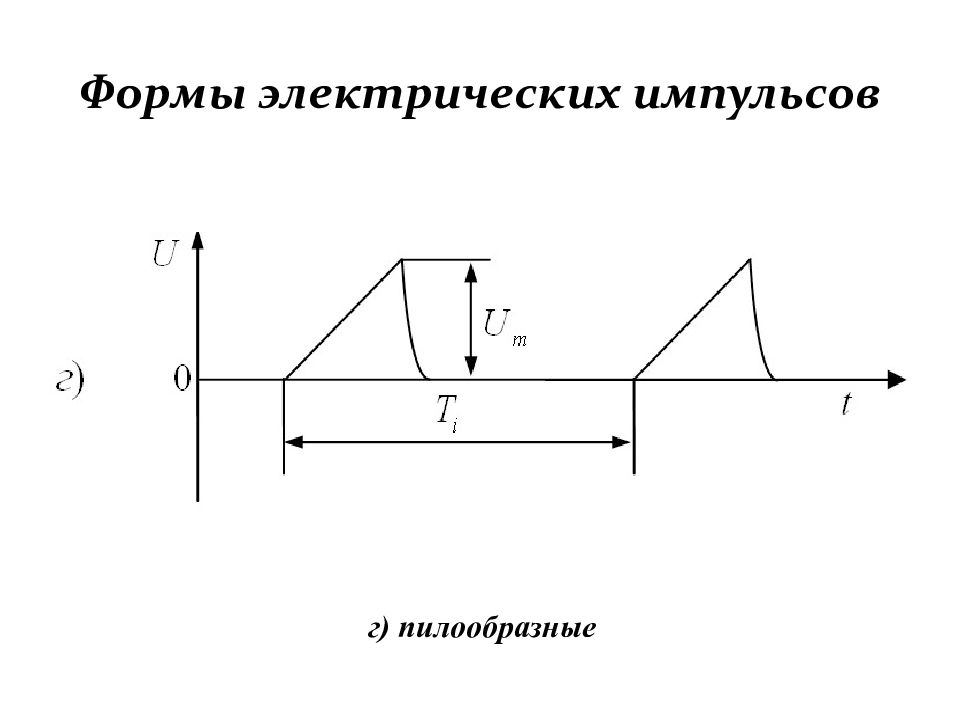
Первый слайд презентации: Формирование и генерирование электрических импульсов
Импульсная техника
Слайд 2: Рекомендуемая литература
Браммер Ю.А., Пащук И.Н. Импульсные и цифровые устройства. – 2003 г. Гольденберг Л.М. Импульсные устройства. – 1981 г. Под ред. Яковлева В.Н. Справочник по импульсной технике. – 1972 г. А.А. Зайцев, Э.И. Исакович, П.П. Мухлынин, Н.А. Фортунова Электронные средства информационных систем, часть 4. Формирование и генерирование электрических импульсов. – 2012 г.
Слайд 3: Задачи импульсной техники
Импульсная техника решает следующие задачи: Формирование импульсов; Генерирование импульсов; Управление импульсами.
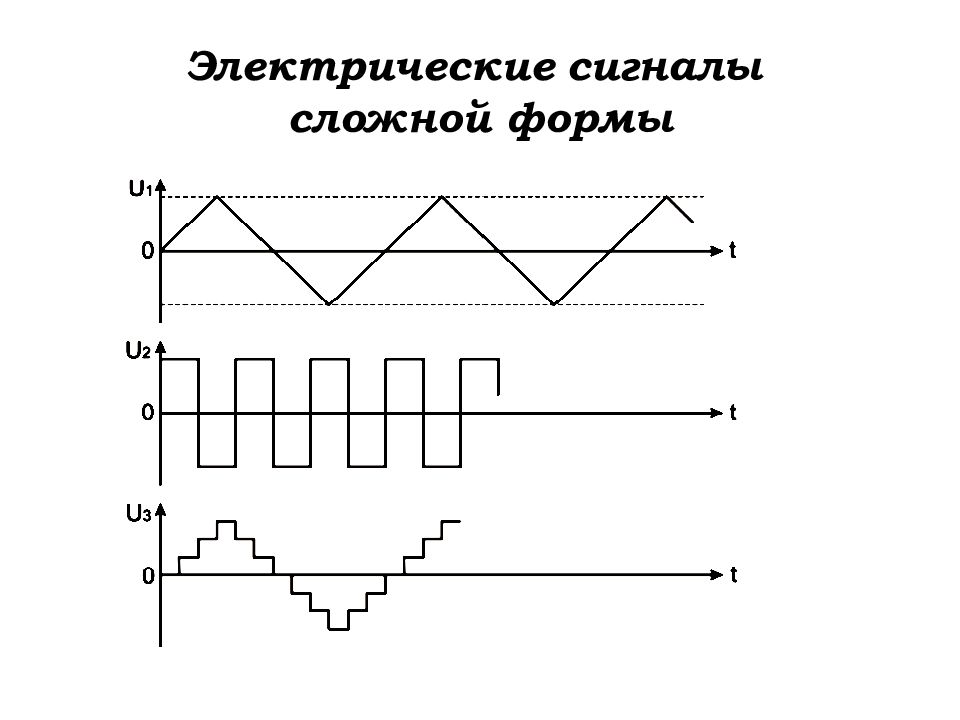
Слайд 4: Сигналы импульсных устройств
Сигналом называют физический процесс, несущий информацию. Сигналы могут быть звуковыми, световыми, электрическими. Информация сосредоточена в изменениях параметров физического процесса. Если параметры процесса не меняются, то он не является сигналом. Так, например, неизменный по тональности и громкости звук, световой поток или синусо-идальное электрическое колебание с постоянной амплитудой или частотой никакого сообщения не содержат. Наоборот, в изме-нениях громкости и тона звука, яркости и цвета светового излучения, амплитуды, частоты или фазы электрического колебания запечатлена информация. Информативным является также появление или окончание, например, электрического колебания, т.е. его изменения.
Слайд 5: Сигналы импульсных устройств
Сигналы на выходе микрофона, передающей ТВ- камеры, различного рода датчиков аналогичны по своему «рисунку» воздействиям на эти устройства – звуковому давлению, распределению освещённости, температуре и т.п. Поэтому подобные сигналы называют аналоговыми. Между минимальным и максимальным значениями аналоговый сигнал может иметь любое значение. Обычно аналоговые сигналы являются непрерывными. Устройства, в которых производится обработка таких сигналов, называются аналоговыми.
Слайд 6: Переходные процессы в электрических цепях
Такому режиму соответствует определённый запас энергии, сосредоточивающийся в реактивных элементах цепи – индуктивностях и ёмкостях. Всякий режим, длительно существующий в электрической цепи и характеризующийся неизменными значениями токов и напряже-ний, называется стационарным (установившимся) режимом. Любые изменения нагрузки или напряжения источника питания (включение или выключение его) приводят в итоге к новому установившемуся режиму с другими значениями токов, напряжений и, следовательно, запасом энергии в реактивных элементах.
Слайд 7: Переходные процессы в электрических цепях
Переход от одного стационарного состояния к другому называется переходным (нестационарным) процессом, который связан с изменением запаса энергии. Всякое изменение запаса электрической или магнитной энергии не может происходить мгновенно, а сопровождается процессом установления нового энергетического режима в цепи. При воздействии на вход электрической цепи импульсов с крутым фронтом без особых погрешностей можно полагать, что воздействие этого импульса на электрическую цепь происходит скачкообразно, подобно мгновенному включению или выключению напряжения (тока).
Слайд 8: Переходные процессы в электрических цепях
Теоретически можно считать, что коммутация цепи (т.е. изменение параметров цепи или схемы самой цепи) происходит мгновенно, т.е. на включение и выключение цепи время не расходуется. Тем не менее, переход от одного режим работы цепи к другому происходит не мгновенно, а в течение некоторого промежутка времени. Объясняется это тем, что каждому состоянию цепи соответствует определённый запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей.
Слайд 9: Энергия реактивных элементов
Энергия магнитного поля и электрического поля не может мгновенно изменяться. Энергия может изменяться только плавно. ………(1.1) ………(1.2)
Слайд 10: Энергия реактивных элементов
Если попытаться предположить обратное, то на индуктив-ности появилось бы бесконечно большое напряжение: (где – поток магнитной индукции), что лишено физического смысла так как
Слайд 11: Энергия реактивных элементов
A налогично невозможно себе представить скачкообразное изменение электрического поля ёмкости, так как в противном случае через ёмкость должен был бы протекать бесконечно большой ток что также лишено физического смысла.
Слайд 12: Постоянная времени электрической цепи
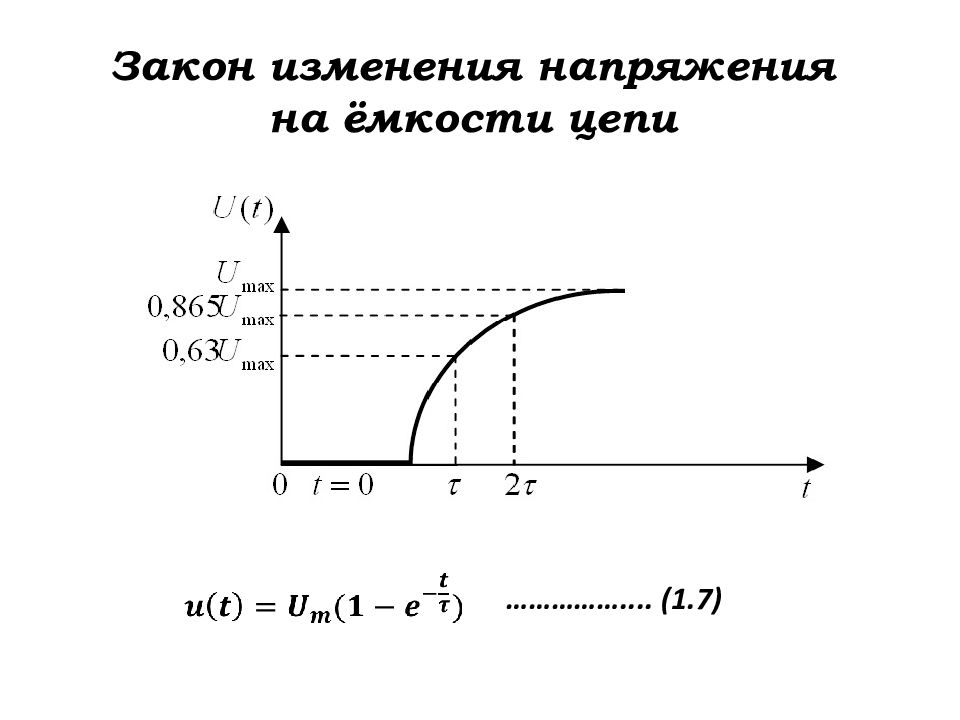
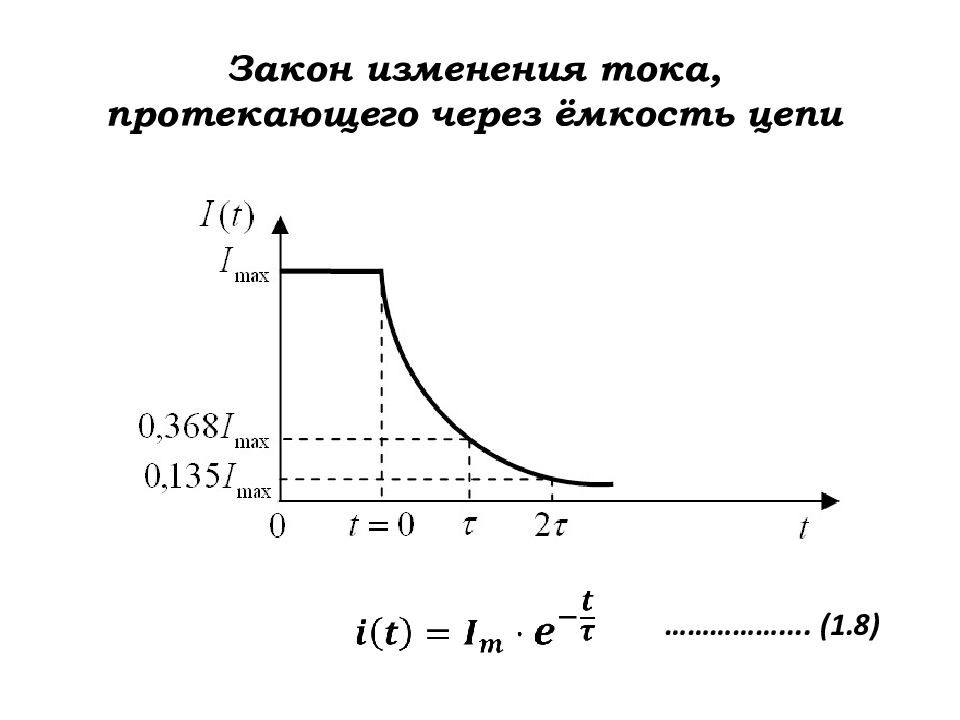
Ток заряда ёмкости С : Напряжение на выходе цепи : ………. (1.4) …………(1.3) В ыражение (1.4) называется экспоненциальной функцией. Другая её запись: ………. (1.5)
Слайд 15: Постоянная времени цепи
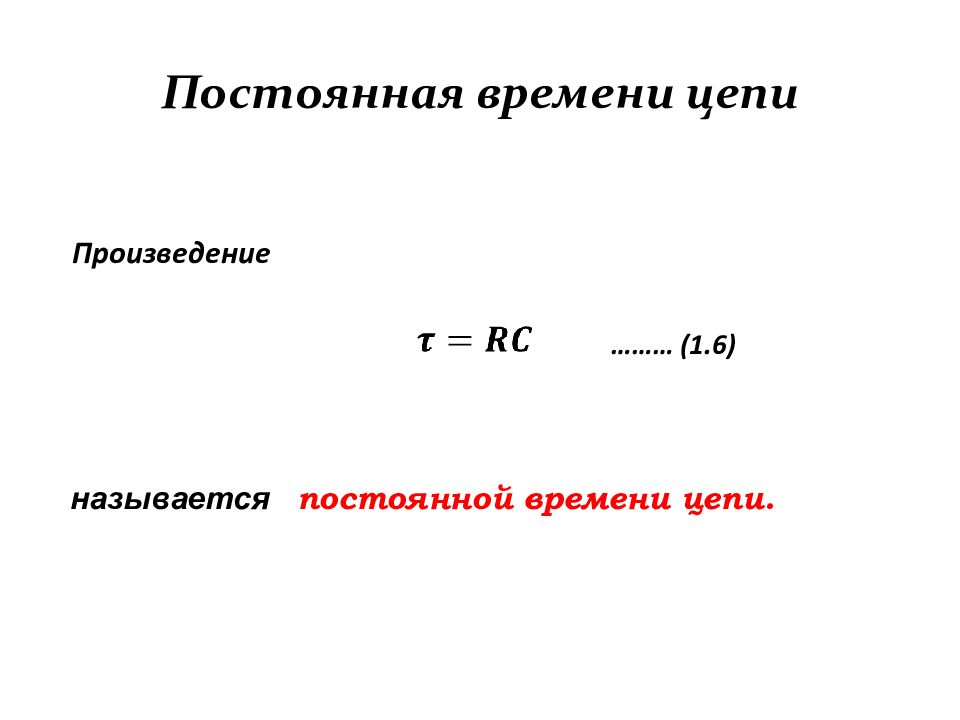
Произведение называется постоянной времени цепи. ……… (1.6)
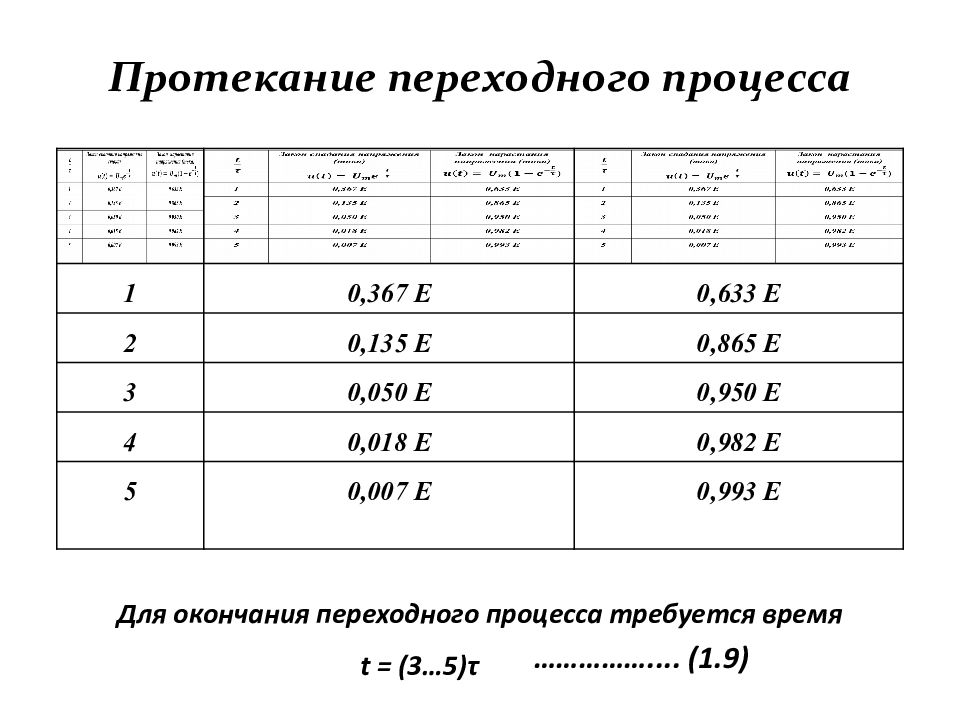
Слайд 20: Протекание переходного процесса
1 0,367 Е 0,633 Е 2 0,135 Е 0,865 Е 3 0,050 Е 0,950 Е 4 0,018 Е 0,982 Е 5 0,007 Е 0,993 Е Для окончания переходного процесса требуется время t = (3…5) τ …………….... (1.9)
Слайд 21: Законы коммутации
В импульсной технике принимают следующие допущения, позволяющие упростить анализ электрических цепей с сосредото-ченными параметрами. Эти допущения носят название законов коммутации: 1. Токи, протекающие через резисторы и ёмкости, могут изменяться скачкообразно. 2. Напряжения на индуктивностях и резисторах изменяться скачкообразно. могут
Слайд 22: Законы коммутации
Первый закон коммутации можно объяснить следующим образом. Известно, что ток, протекающий через ёмкость, и напряжение на этой ёмкости связаны следующими соотношениями: …………….... (1.10) …………….... (1.11)
Слайд 23: Законы коммутации
Аналогично можно объяснить второй закон коммутации. Известно, что напряжение, приложенное к индуктивности, и протекающий через неё ток связаны следующими соотношениями: …………….... (1.12) …………….... (1.13)
Слайд 24: Законы коммутации
Наличие переходных процессов является причиной искажения формы импульсов, действующих в линейной цепи. Если бы все процессы в цепи устанавливались мгновенно, то никаких искажений импульсов в линейной цепи не было бы.
Слайд 25: Электрические импульсы и их параметры
Под электрическим импульсом понимают отклонение напряжения или тока от некоторого постоянного уровня (в частности, от нулевого), наблюдаемое в течение времени, меньшего или сравнимого с длительностью переходных процессов в схеме.
Слайд 26: Переходный процесс
Под переходным процессом понимается всякое резкое изменение установившегося режима в электрической цепи за счёт действия внешних сигналов или переключений внутри самой цепи. Таким образом, переходный процесс – это процесс перехода электрической цепи из одного стационарного состояния в другое. Как бы ни был короток этот переходный процесс, – он всегда конечен во времени. Для цепей, в которых время существования переходного процесса несравненно меньше времени действия внешнего сигнала (напряжения или тока), режим работы считается установив-шимся, а сам внешний сигнал для такой цепи не является импульсным. Примером этого может служить срабатывание электромагнитного реле.
Слайд 27: Переходный процесс
Когда же длительность действующих в электрической цепи сигналов напряжения или тока становится соизмеримой с дли-тельностью процессов установления, переходный процесс оказывает настолько сильное влияние на форму и параметры этих сигналов, что их нельзя не учитывать. В этом случае бóльшая часть времени воздействия сигнала на электрическую цепь совпадает со временем существования переходного процесса. Режим работы цепи во время действия такого сигнала будет нестационарным, а воздействие его на электрическую цепь – импульсным.
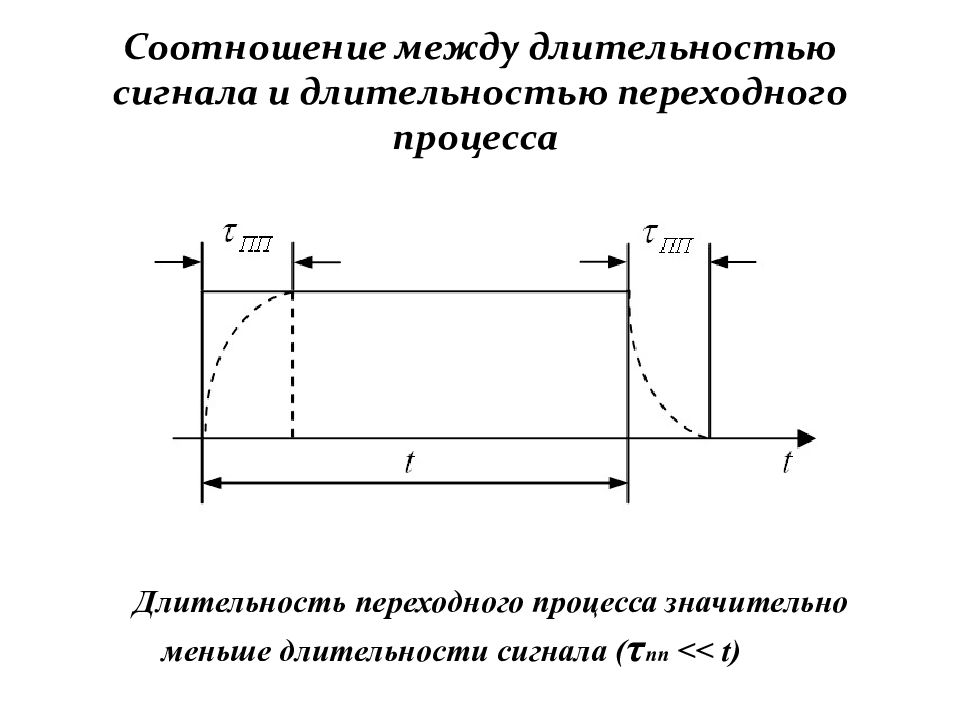
Слайд 28: Соотношение между длительностью сигнала и длительностью переходного процесса
Д лительность переходного процесса значительно меньше длительности сигнала ( τ пп << t )
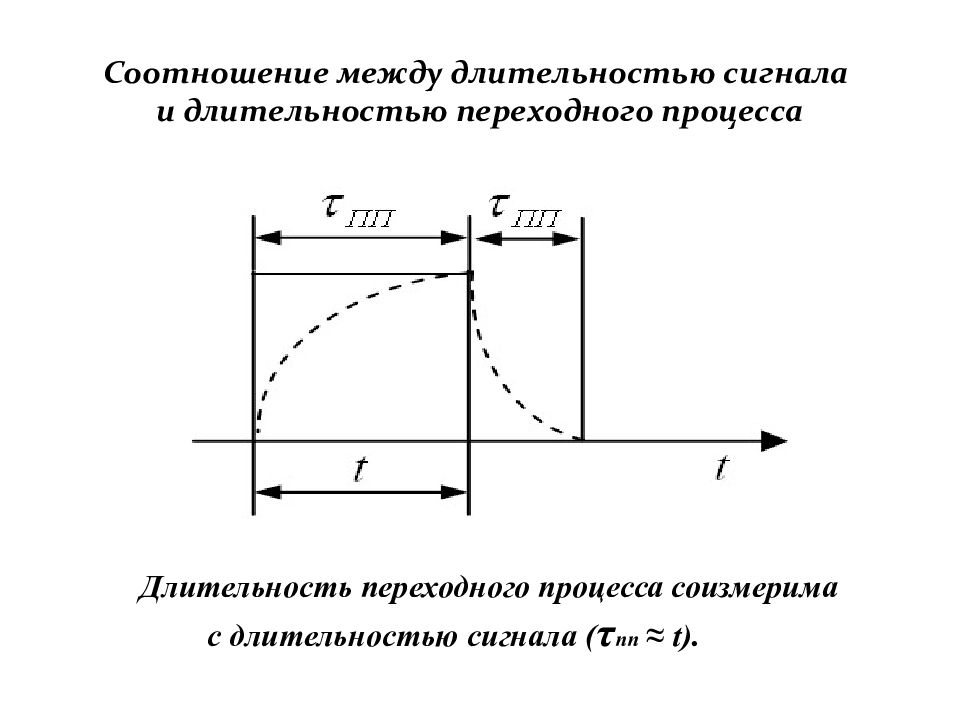
Слайд 29: Соотношение между длительностью сигнала и длительностью переходного процесса
Д лительность переходного процесса соизмерима с длительностью сигнала ( τ пп ≈ t).
Слайд 30: Что такое «электрический импульс»?
Электрическим импульсом для данной цепи называется напряже- ние или ток, действующие в течение промежутка времени, соизмеримого с длительностью переходного процесса в этой цепи. При этом предполагается, что между двумя последовательно действующими в цепи импульсами должен быть достаточный промежуток времени, превышающий длительность процесса установления. В противном случае вместо импульсов будут возникать сигналы сложной формы.
Слайд 39: Параметры импульса
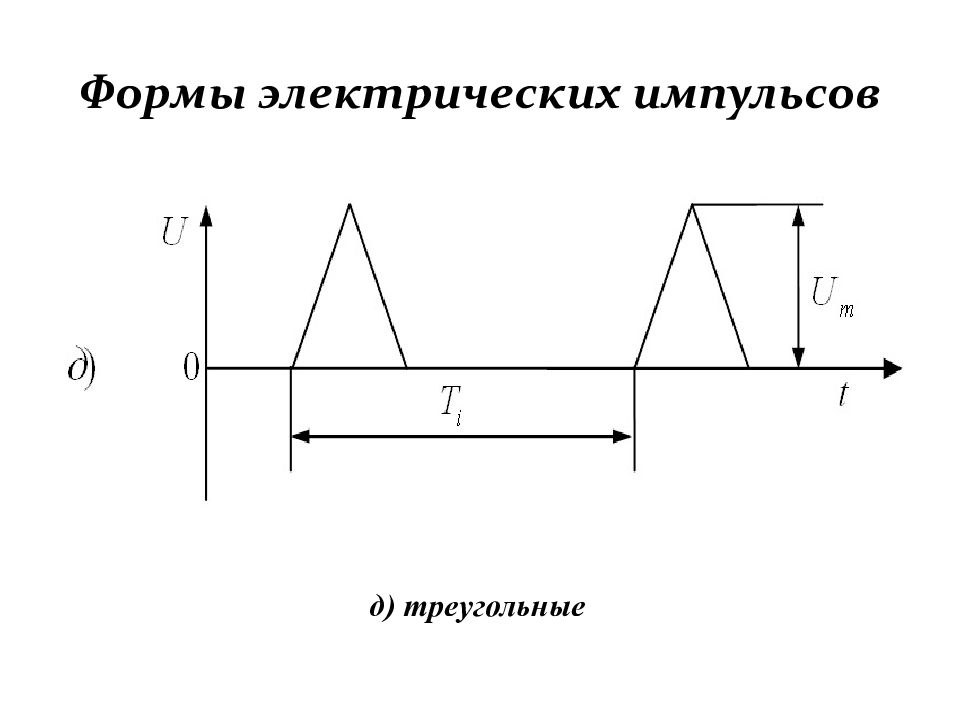
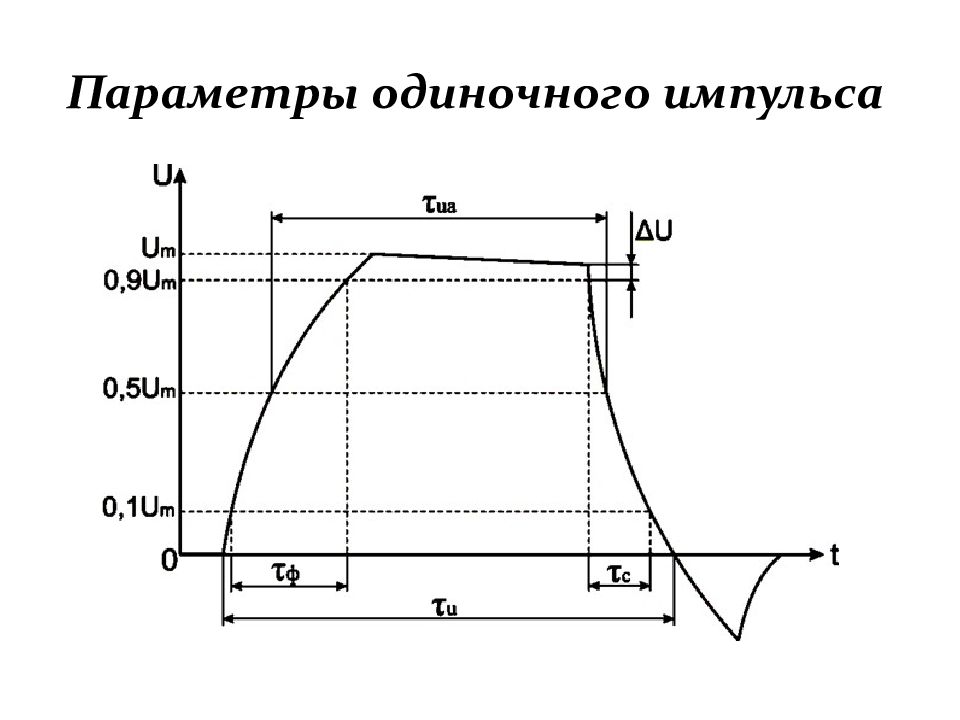
Форму импульсов и свойства отдельных его участков с количественной стороны оценивают следующими параметрами: – длительность импульса. Обычно измерения длитель-ности импульсов или отдельных участков производят на определённом уровне от их основания. Если это не оговаривается, то длительность импульса определяется на нулевом уровне. Однако чаще всего длительность импульса определяется на уровне или считая от основания. В последнем случае длительность
Слайд 41: Параметры импульса
Участок импульса между фронтами называют плоской вершиной. …………….... (1.15)
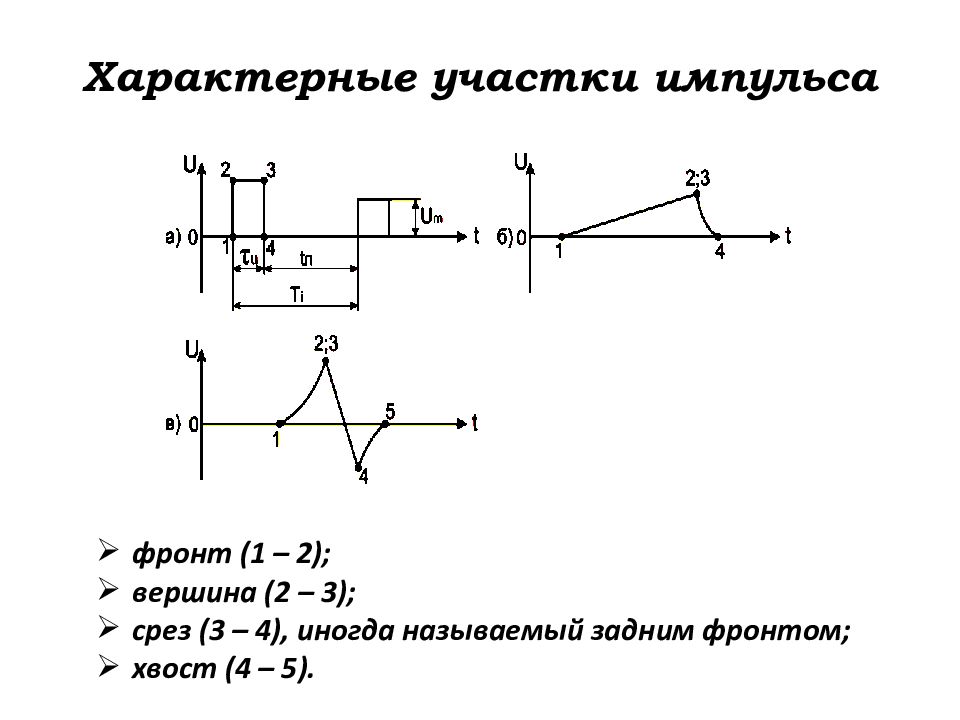
Слайд 42: Характерные участки импульса
фронт (1 – 2); вершина (2 – 3); срез (3 – 4), иногда называемый задним фронтом; хвост (4 – 5).
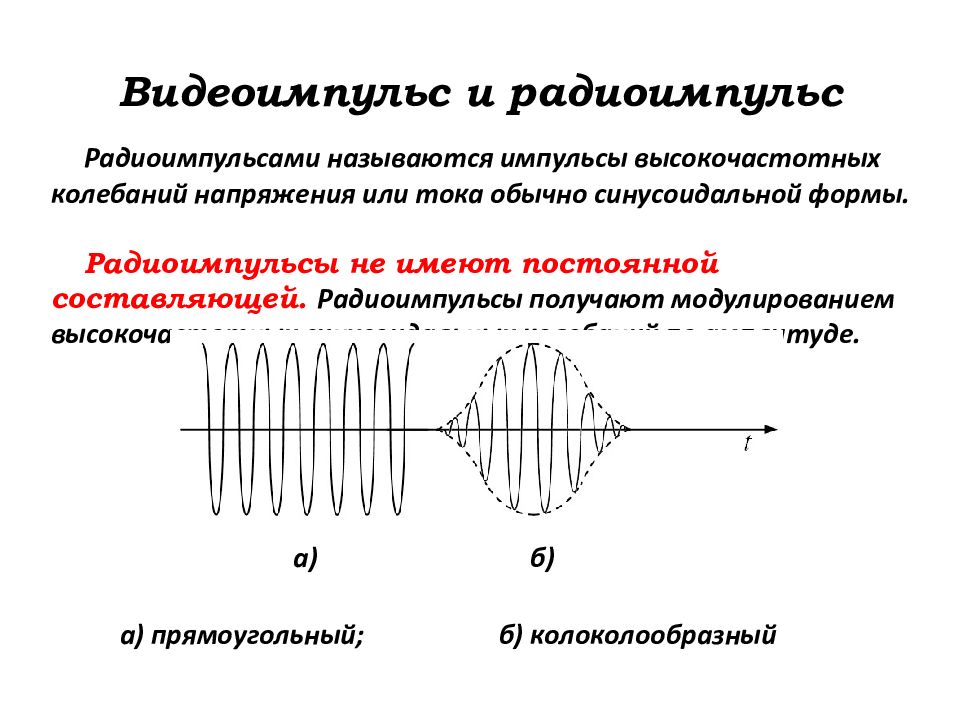
Слайд 43: Видеоимпульс и радиоимпульс
Радиоимпульсами называются импульсы высокочастотных колебаний напряжения или тока обычно синусоидальной формы. Радиоимпульсы не имеют постоянной составляющей. Радиоимпульсы получают модулированием высокочастотных синусоидальных колебаний по амплитуде. а) прямоугольный; б) колоколообразный а) б)
Слайд 45: Периодическая последовательность импульсов
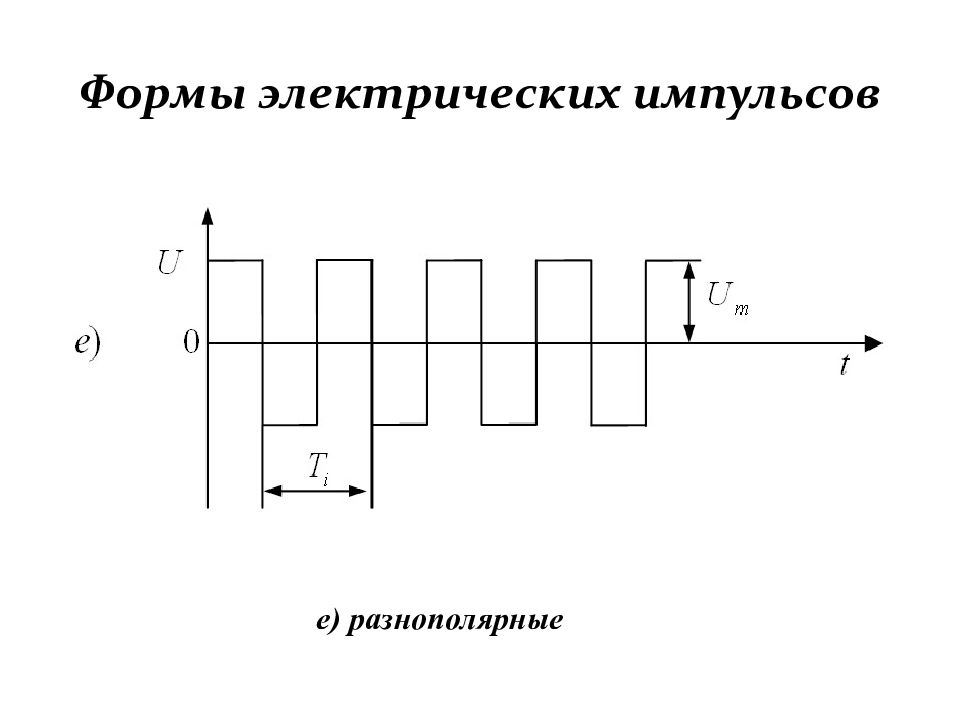
Электрические импульсы, следующие друг за другом через равные промежутки времени, называются периодической последователь-ностью. Периодическая последовательность импульсов характеризуется следующими параметрами: 1. Период повторения – промежуток времени между началом двух соседних однополярных импульсов. Он выража - ется в секундах (с) или дольных единицах секунды (мс; мкс; нс). Величина, обратная периоду повторения, называется частотой повторения (следования) импульсов. Она определяет количество импульсов, в течение одной секунды и выражается в герцах (Гц), килогерцах (кГц) и т.д. …………….... (1.1 6 )
Слайд 46: Периодическая последовательность импульсов
……… (1.18) ……… (1.17) Скважность – безразмерная величина, которая может изме-няться в очень широких пределах, так как длительность импульсов может быть в сотни и даже тысячи раз меньше периода импульсов или, наоборот, занимать большую часть периода.
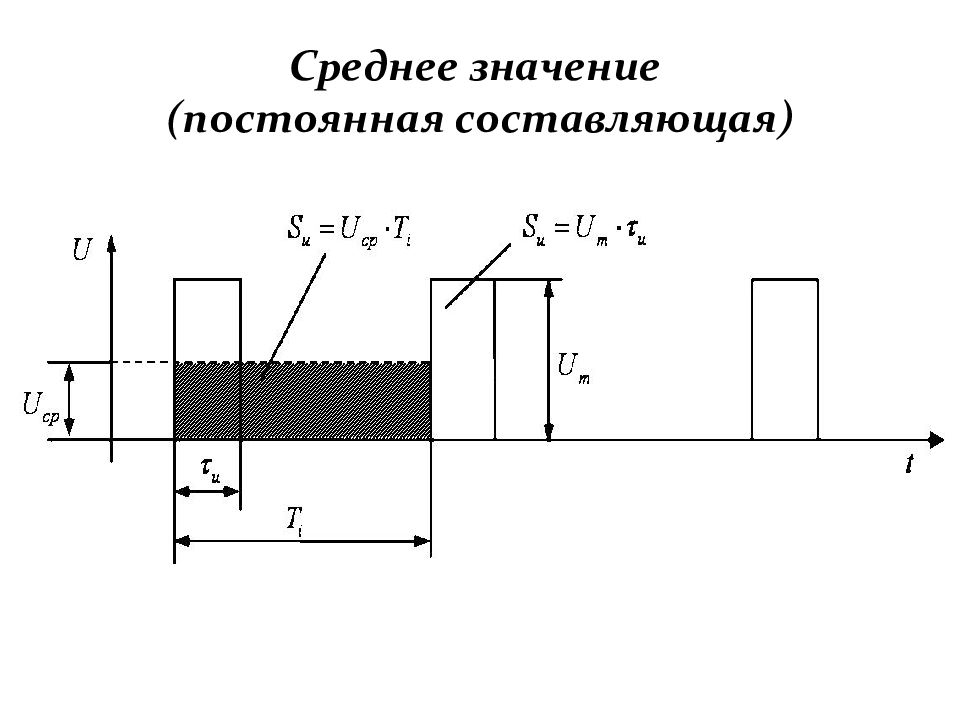
Слайд 48: Среднее значение последовательности импульсов (постоянная составляющая)
Для периодической последовательности импульсов прямо-угольной формы, у которой U (t) = U m, период повторения Т i и длительность импульса τ и, это выражение после подстановки и преобразования принимает вид: ……… (1.19) ……… (1.20)
Слайд 49: Среднее значение последовательности импульсов (постоянная составляющая)
Из рис. 1.10 видно, что откуда следует: ……… (1.21) ……… (1.22)
Слайд 50: Среднее значение последовательности импульсов (постоянная составляющая)
откуда следует ……… (1.23) и ……… (1.24)
Слайд 52: Линейные цепи
Элемент, параметры которого (сопротивление, индуктивность, ёмкость) не зависят от величины и направления токов и приложенных напряжений, называется линейным. Цепи, содержащие линейные элементы, называются линейными. Свойства линейных цепей: Вольт-амперная характеристика (ВАХ) линейной цепи представляет собой прямую линию, т.е. величины токов и напряжений будут связаны между собой линейными уравнениями . 2. Для расчёта (анализа) и синтеза линейных цепей применим принцип суперпозиций (наложения). с постоянными коэффициентами. Пример ВАХ такого вида – закон Ома.
Слайд 53: Линейные цепи
3. Линейная цепь не преобразует спектр электрического сигнала. Она может изменить составляющие спектра только по амплитуде и фазе. Это является причиной возникновения линейных искажений. 4. Всякая реальная линейная цепь искажает форму сигнала за счёт переходных процессов и конечной ширины полосы пропускания.
Слайд 54: Линейные цепи
Это объясняется тем, что гармоники входного напряжения по-разному пропускаются такой цепью. В результате прохождения входного сигнала через ёмкости и индуктивности цепи соотноше-ния между гармоническими составляющими на элементах цепи изменяются по амплитуде и фазе по отношению к входному сигналу. В результате соотношения между амплитудами и фазами гармоник на входе цепи и на её выходе не одинаковы. Это свойство положено в основу формирования импульсов с помощью линейных цепей.
Слайд 55: Нелинейные цепи
Элемент, параметры которого зависят от величины и полярно-сти приложенных напряжений или протекающих токов, называет-ся нелинейным, а цепь, содержащую такие элементы, называют нелинейной. Свойства нелинейных цепей: 1. Ток, протекающий через нелинейный элемент, не пропорционален приложенному к нему напряжению, т.е. зависимость между напряжением и током (ВАХ) носит нелинейный характер. Примером такой ВАХ служат входные и выходные характеристики ЭВП и ППП. К нелинейным элементам относятся электровакуумные приборы (ЭВП), полупроводниковые приборы (ППП), работающие на нелинейном участке ВАХ, диоды (вакуумные и полупроводниковые), а также трансформаторы с ферромагнетиками.
Слайд 56: Нелинейные цепи
2. Процессы, протекающие в нелинейных цепях, описываются нелинейными уравнениями различного вида, коэффициенты которых зависят от самой функции напряжения (тока) или от её производных, а ВАХ нелинейной цепи имеет вид кривой или ломаной линии. Примером могут служить характеристики диодов, триодов, тиристоров, стабилитронов и др. 3. Для нелинейных цепей принцип суперпозиций неприменим. При воздействии внешнего сигнала на нелинейные цепи в них всегда возникают токи, содержащие в своём составе новые частотные составляющие, которых не было во входном сигнале. Это является причиной возникновения нелинейных искажений, в результате чего сигнал на выходе нелинейной цепи всегда отличается по форме от входного сигнала.
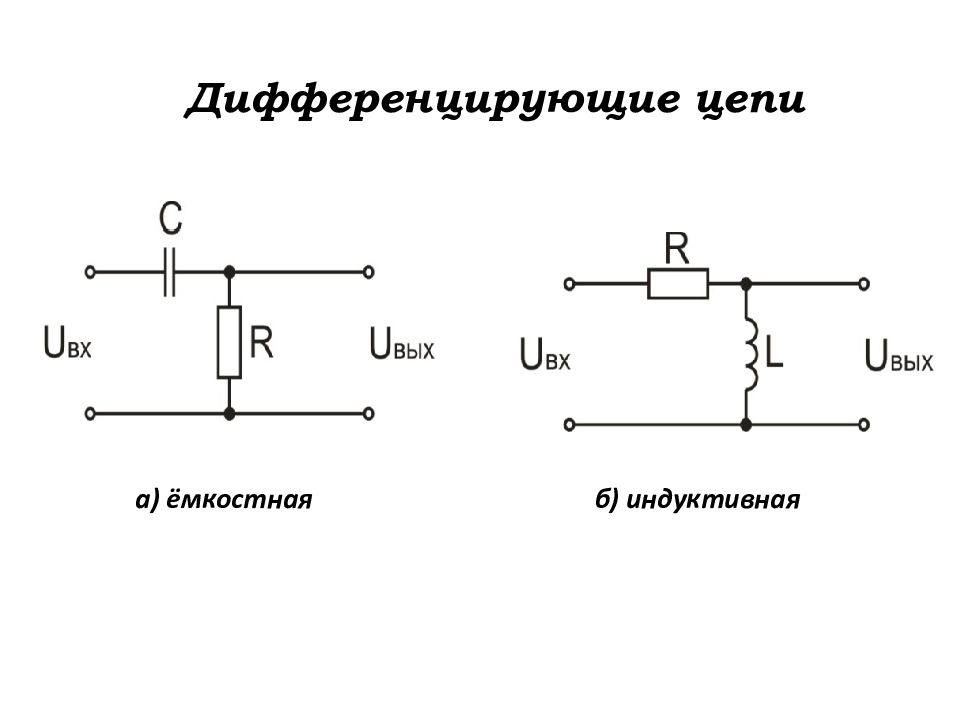
Слайд 57: Дифференцирующие цепи
Дифференцирующей называется цепь, на выходе которой напряжение пропорционально первой производной от входного напряжения. ...... (1)
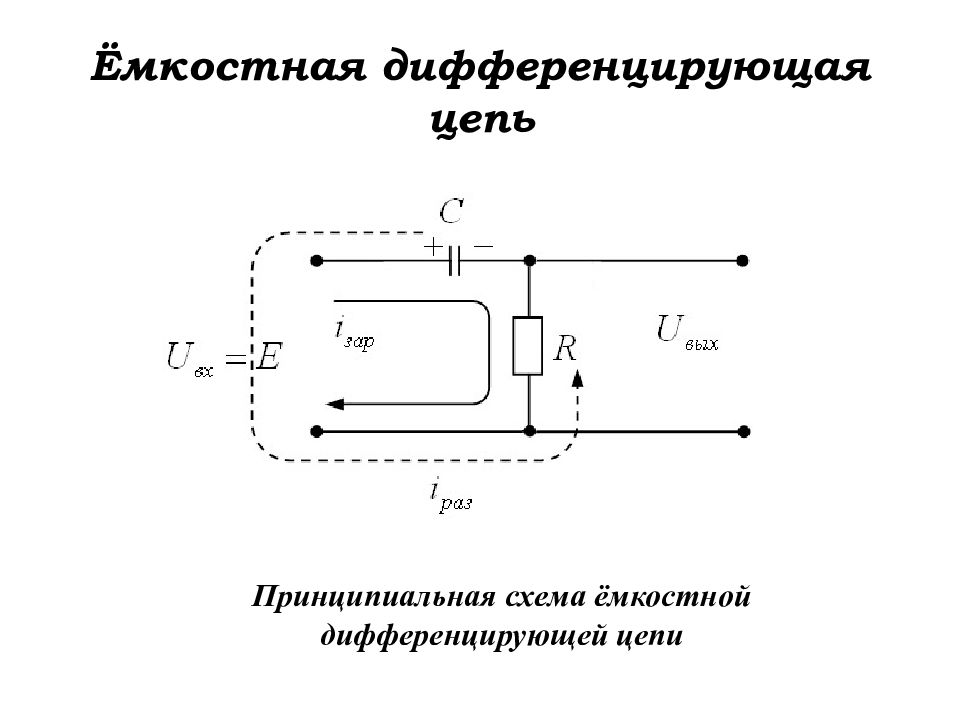
Слайд 59: Ёмкостная дифференцирующая цепь
Принципиальная схема ёмкостной дифференцирующей цепи
Слайд 60: Ёмкостная дифференцирующая цепь
Ток, протекающий через ёмкость: Из схемы ДЦ видно, что Выходное напряжение ...... (2 ) ..... (3) Подставив (1) в (2), получим: Если выбрать достаточно малую величину R, чтобы то получим приближённое равенство: ...... (4) , ...... (5)
Слайд 61: Ёмкостная дифференцирующая цепь
т.е. где – верхняя граничная частота гармоники выходного сигнала, ещё имеющая существенное значение для формы выходного импульса. Коэффициент пропорциональности носит название постоянной времени дифференцирующей цепи и имеет размерность времени.
Слайд 62: Постоянная времени цепи
В соответствии с Международной системой единиц (СИ) единица измерения электрического сопротивления а единица измерения электрической ёмкости Следовательно,
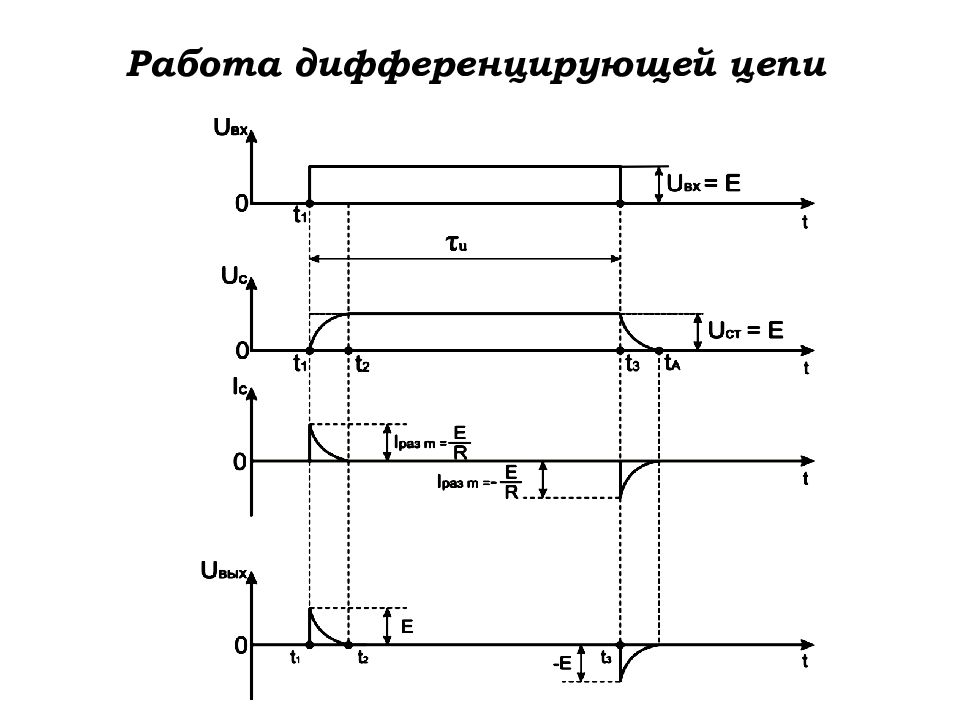
Слайд 64: Работа дифференцирующей цепи
Пусть на вход подаётся идеальный прямоугольный импульс, у которого τ ф = τ с = 0, а внутреннее сопротивление источника сиг-нала R i = 0. Пусть импульс определяется следующим выражением: 1. Исходное состояние схемы (t < t 1 ). В исходном состоянии U вх = 0; U с = 0; i с = 0; U вых = 0. 2. Первый скачок напряжения (t = t 1 ).
Слайд 65: Работа дифференцирующей цепи
3. Заряд конденсатора (t 1 < t < t 2 ). Напряжение на конденсаторе будет нарастать по экспоненциаль-ному закону: Напряжение на выходе ДЦ будет падать по мере нарастания напряжения заряда на конденсаторе: ...... (6) ...... (7)
Слайд 66: Работа дифференцирующей цепи
Т.к. в любой момент времени для делителя напряжения выполня-ется равенство то 4. Окончание заряда конденсатора (t = t 2 ). Напряжение на выходе дифференцирующей цепи достигает практически нулевого значения, т.е. в момент времени t = t 2
Слайд 67: Работа дифференцирующей цепи
5. Установившийся режим (t 2 < t < t 3 ). При этом 6. Второй скачок напряжения (t = t 3 ). В момент времени t = t 3 напряжение на входе дифференцирующей цепи скачком падает до нуля. Конденсатор C становится источ- ником напряжения, т.к. он заряжен до величины При этом ток разряда в данный момент времени становится максимальным:
Слайд 68: Работа дифференцирующей цепи
Напряжение на выходе дифференцирующей цепи 7. Разряд конденсатора (t 3 < t < t 4 ). После второго скачка напряжение на конденсаторе начинает уменьшаться по экспоненциальному закону: ; ;
Слайд 69: Принцип работы дифференцирующей цепи
8. Окончание разряда конденсатора и восстановление исходного состояния схемы (t ≥ t 4 ). После окончания переходного процесса разряда конденсатора Окончание разряда конденсатора наступает практически при t = (3…5) τ = (3…5) RC.
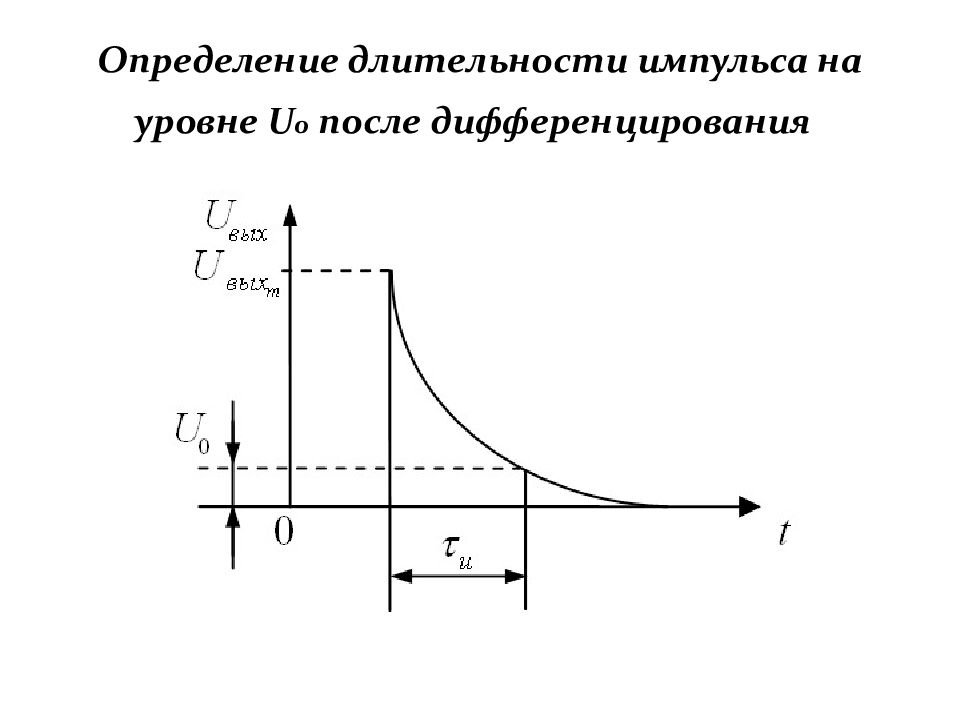
Слайд 70: Определение длительности импульса на уровне U 0 после дифференцирования
Слайд 71: Определение длительности импульса на уровне U 0 после дифференцирования
Длительность продифференцированного импульса на уровне Отсюда: и
Слайд 72: ДЦ как фильтр верхних частот
Изменение формы импульса на выходе дифференцирующей цепи можно объяснить с точки зрения спектрального анализа. Поэтому на выход плоская вершина входного импульса почти не передаётся. Для высокочастотных составляющих входного импульса, формирующих его фронт и срез, Поэтому фронт и срез входного импульса на выход передаются практически без ослабления. Эти соображения позволяют определить дифференцирующую цепь как фильтр верхних частот.
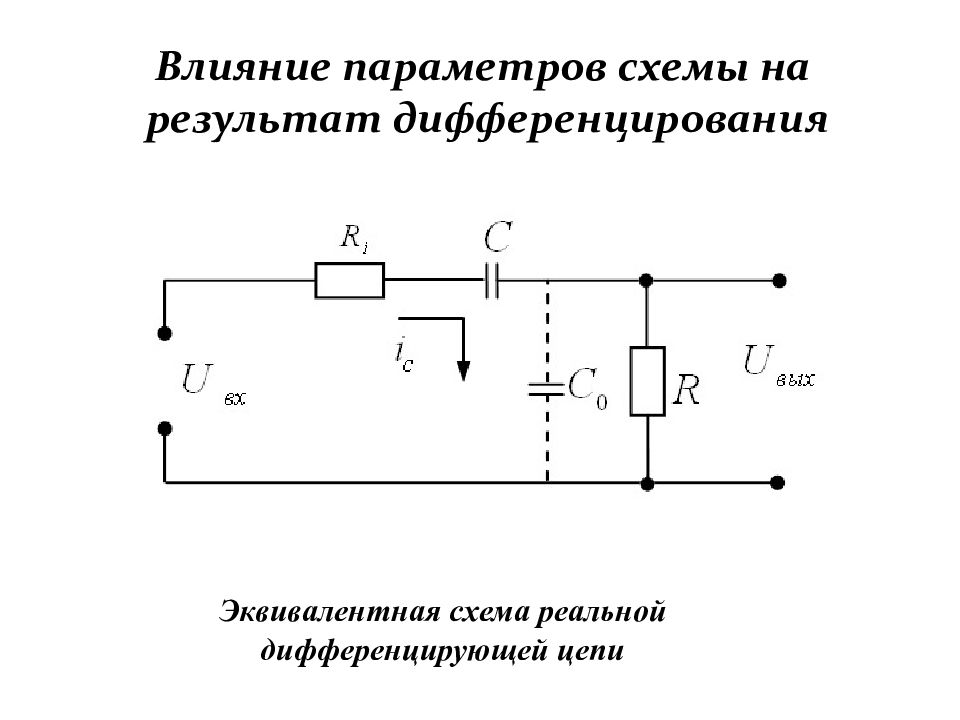
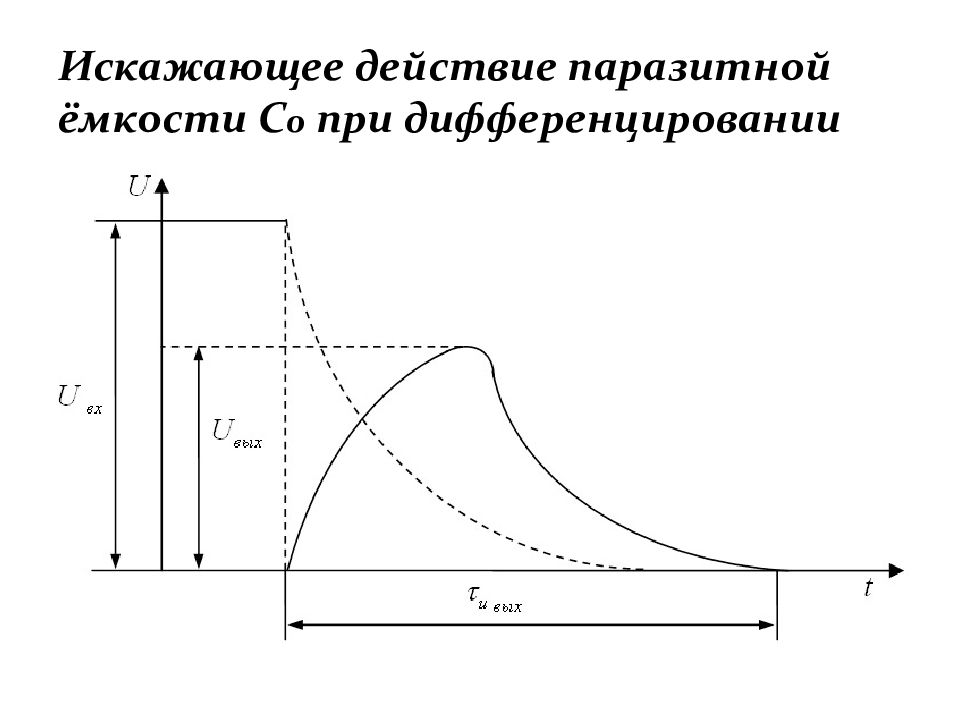
Слайд 73: Влияние параметров схемы на результат дифференцирования
Эквивалентная схема реальной дифференцирующей цепи
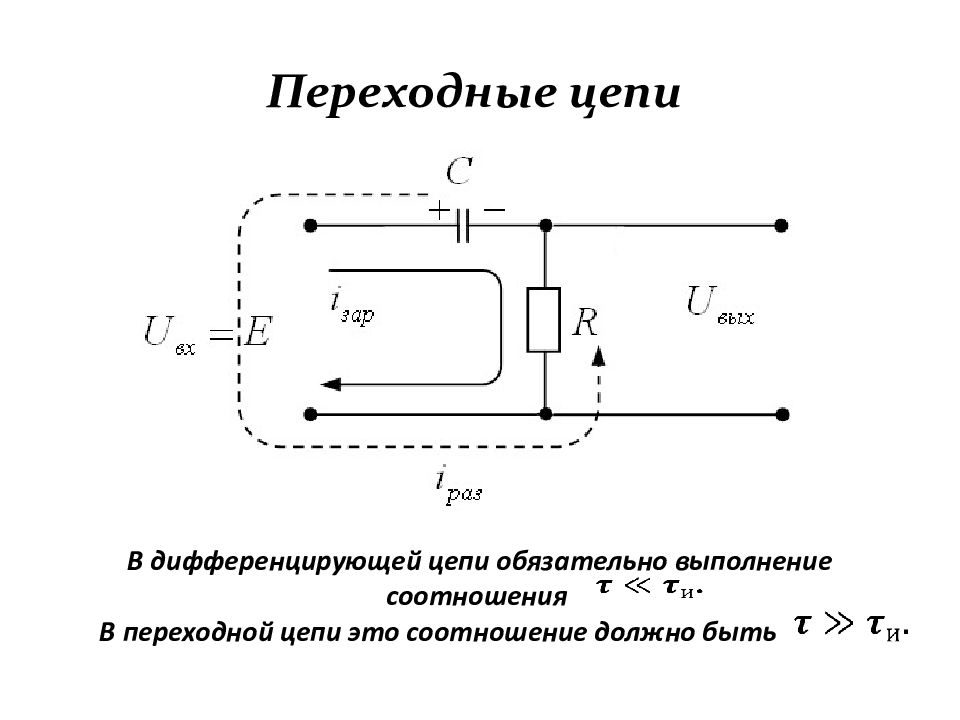
Слайд 75: Переходные цепи
минимальные искажения входного сигнала; разделение («развязка») каскадов по постоянной составляющей. Последнее условие необходимо выполнять, потому что режим работы по постоянному току последующего каскада усиления должен выбираться независимо от постоянной составляющей выходного напряжения предыдущего каскада.
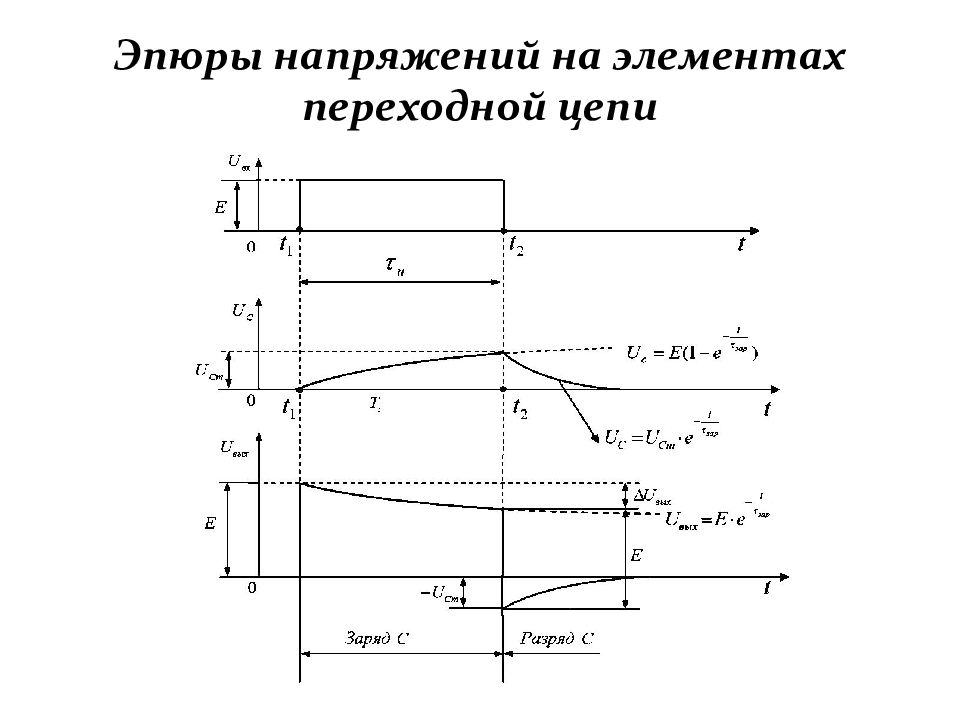
Слайд 76: Переходные цепи
Схема переходной цепи по начертанию ничем не отличается от дифференцирующей цепи. Однако если в дифференцирующей цепи обязательно выполнение соотношения то в переходной цепи это соотношение должно быть
Слайд 77: Переходные цепи
В дифференцирующей цепи обязательно выполнение соотношения В переходной цепи это соотношение должно быть
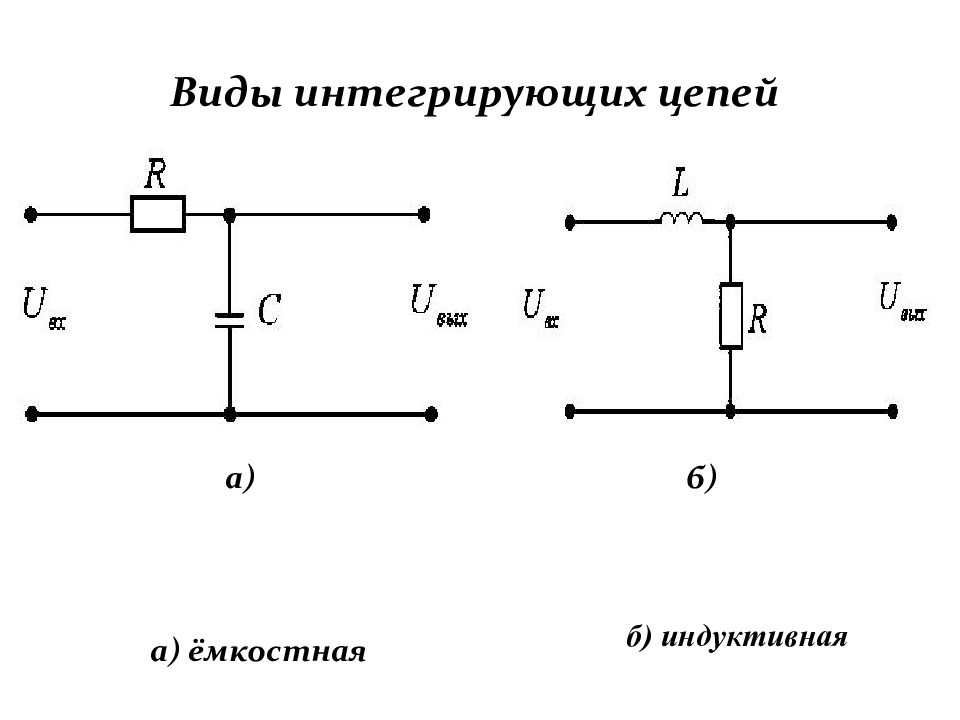
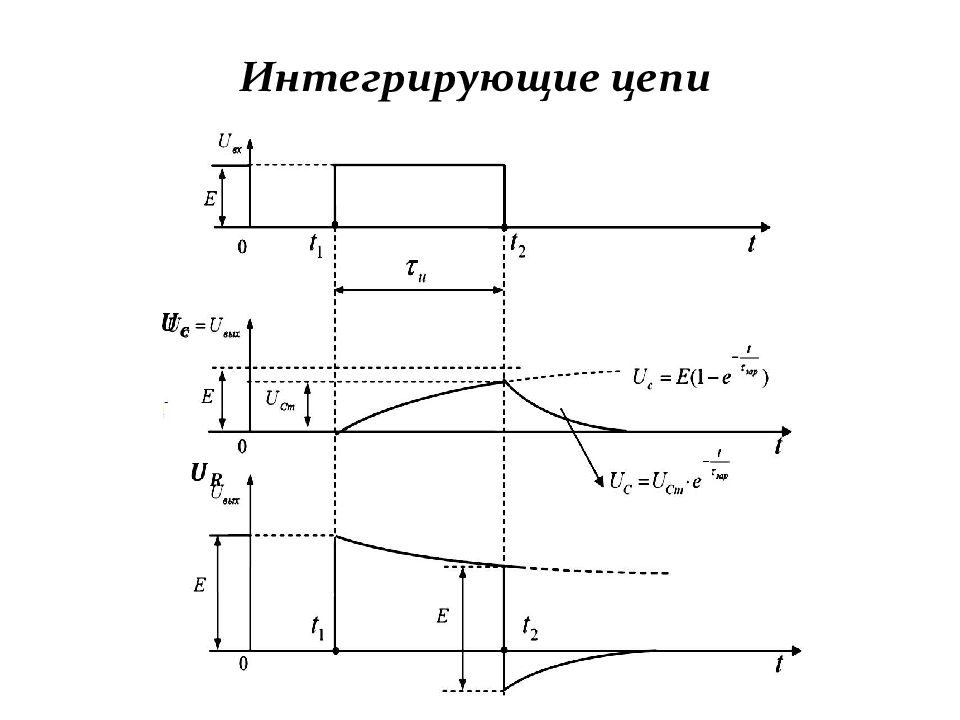
Слайд 79: Интегрирующие цепи
Интегрирующей называется цепь, величина выходного напряжения которой пропорциональна интегралу по времени от величины входного напряжения. Математически это выражается формулой:
Слайд 81: Интегрирующие цепи
Напряжение на конденсаторе и ток, протекающий через него, связаны зависимостью: Интегрирующая цепь представляет собой делитель напряжения, ток через который равен: Отсюда следует:
Слайд 82: Интегрирующие цепи
Если выбрать для высшей гармоники прямоугольного импульса, т.е. то и, следовательно, Тогда последнее выражение примет вид:
Слайд 84: ИЦ как фильтр нижних частот
Существенное изменение формы входного импульса при интегри-ровании можно объяснить с помощью спектрального анализа. Действительно, при Поэтому интегрирующую цепь можно рассматривать как фильтр нижних частот.
Слайд 85: Контур ударного возбуждения
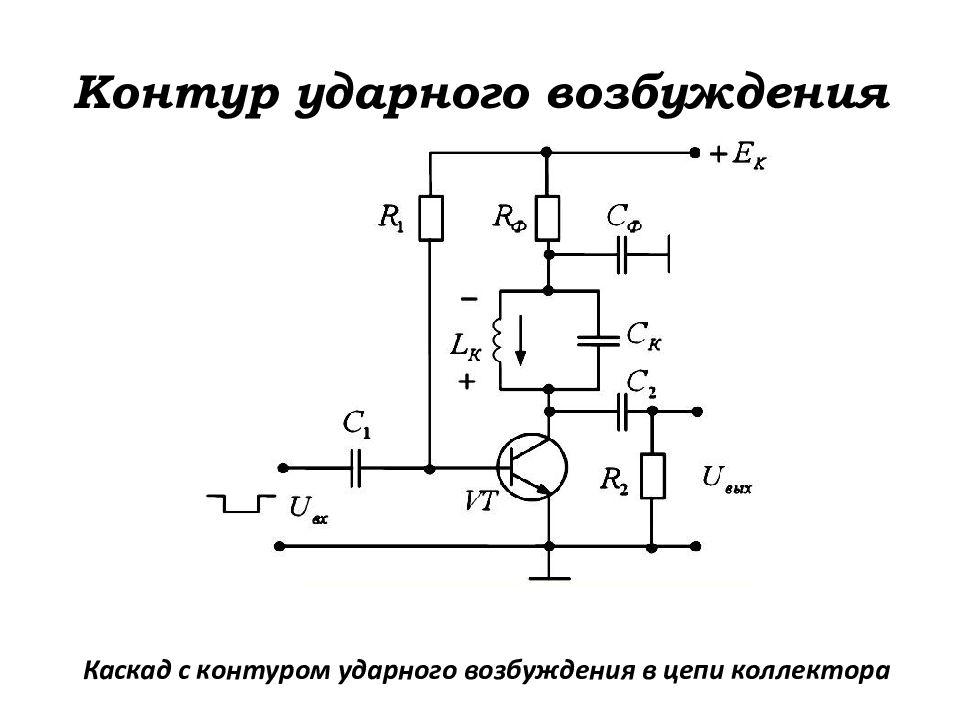
Контур ударного возбуждения (КУВ) формирует пачки синусои-дальных сигналов длительностью, равной длительности импульса на входе генератора. Существуют две разновидности генераторов с КУВ: генератор с КУВ в цепи коллектора; генератор с КУВ в цепи эмиттера.
Слайд 86: Контур ударного возбуждения
Каскад с контуром ударного возбуждения в цепи коллектора
Слайд 87: Контур ударного возбуждения
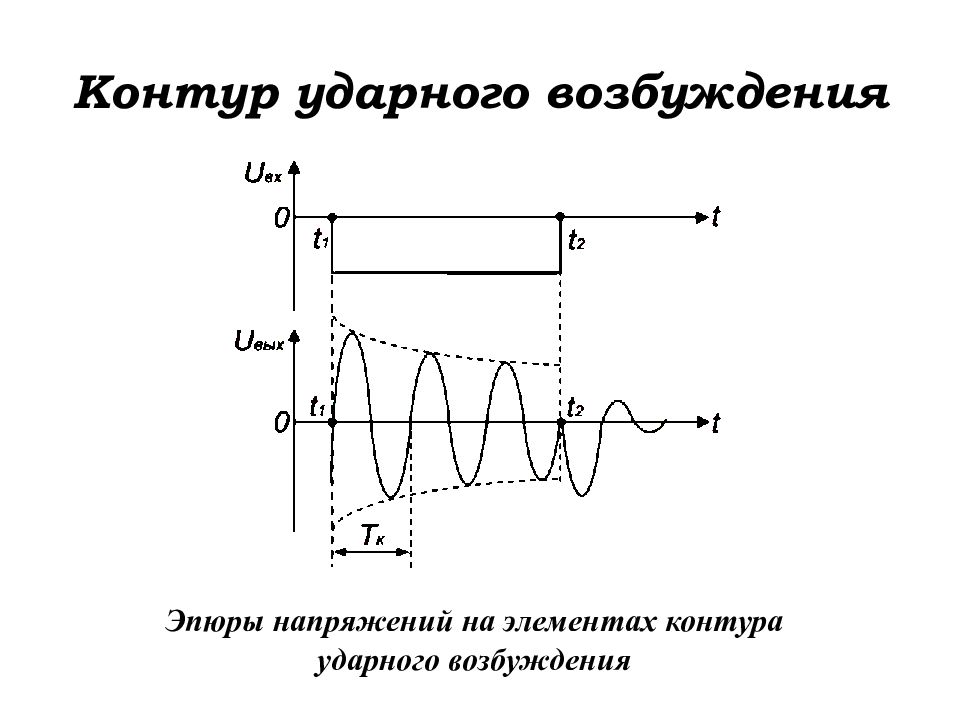
Эпюры напряжений на элементах контура ударного возбуждения
Слайд 88: Контур ударного возбуждения
Выходное напряжение каскада с КУВ представляет собой затуха-ющее по экспоненциальному закону синусоидальное колебание – коэффициент затухания:
Слайд 89: Контур ударного возбуждения
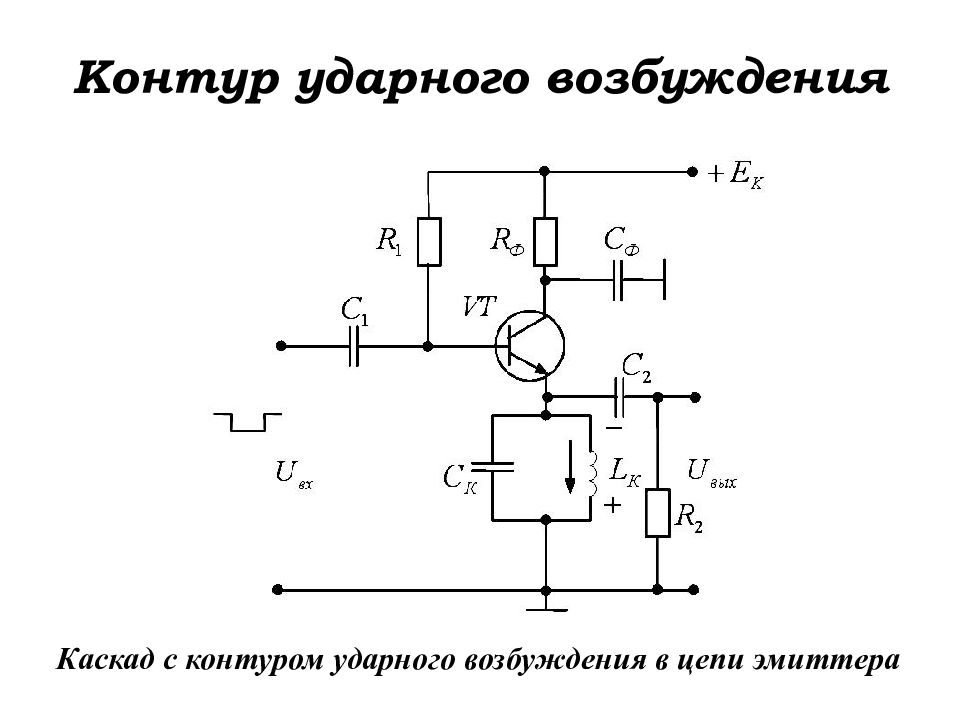
Каскад с контуром ударного возбуждения в цепи эмиттера
Слайд 90: Контур ударного возбуждения
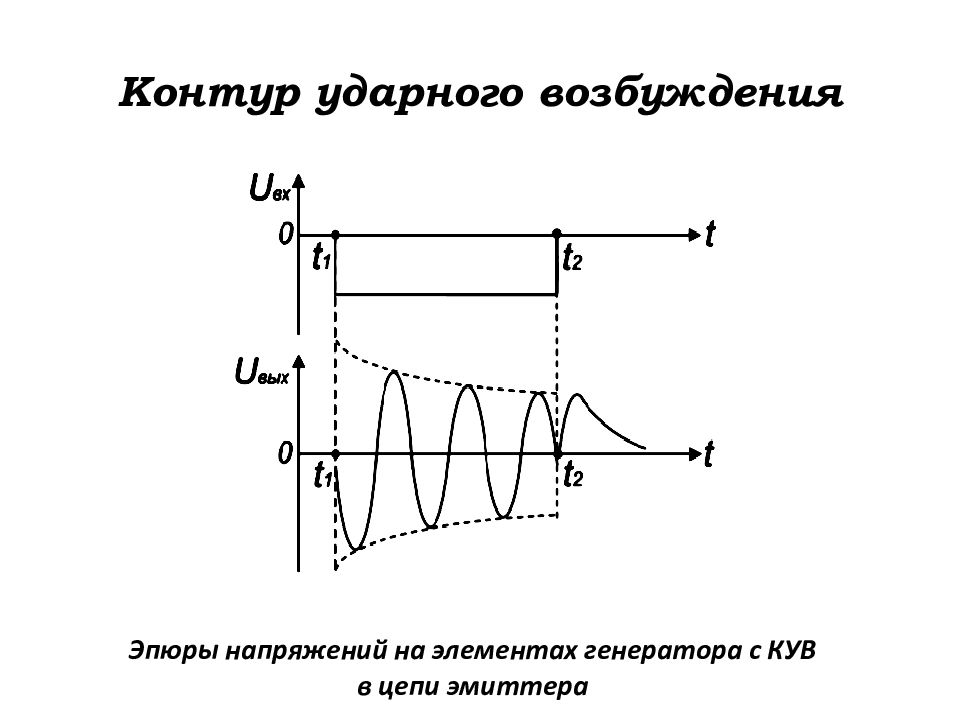
Эпюры напряжений на элементах генератора с КУВ в цепи эмиттера
Слайд 91: Контур ударного возбуждения
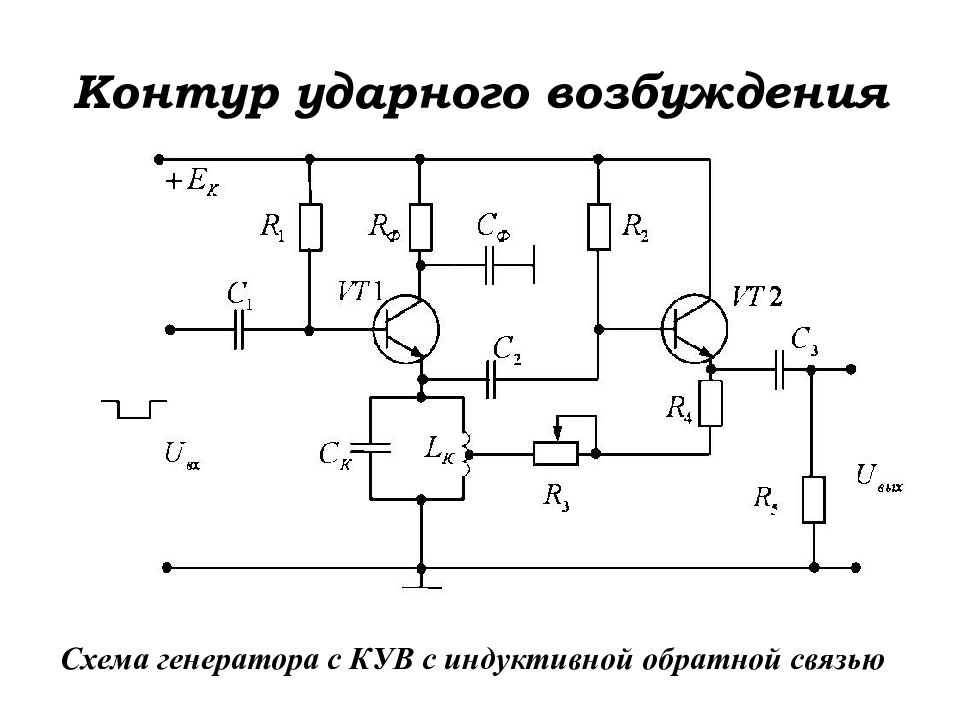
Схема генератора с КУВ с индуктивной обратной связью
Слайд 92: Контур ударного возбуждения
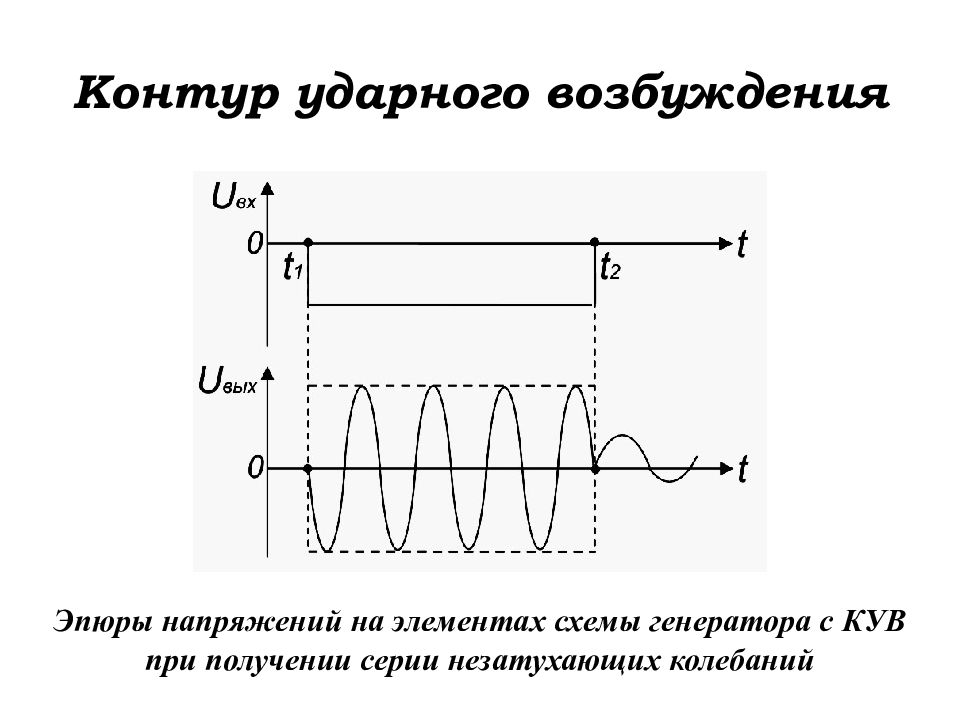
Эпюры напряжений на элементах схемы генератора с КУВ при получении серии незатухающих колебаний
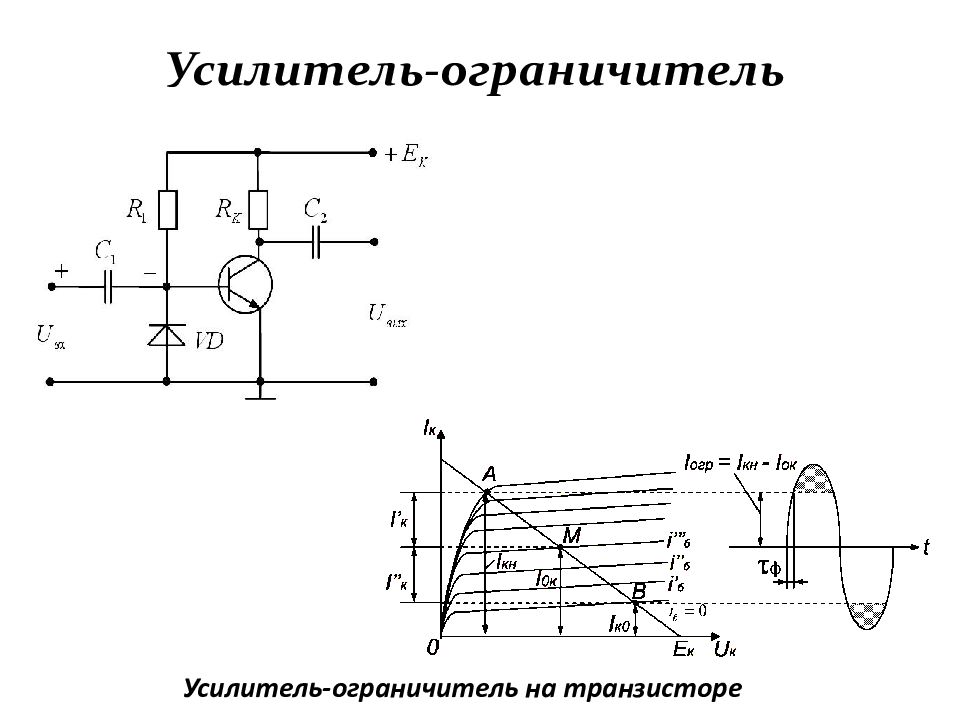
Слайд 93: Ограничители амплитуды
Ограничителем амплитуды называется устройство, напряжение на выходе которого следует за входным напряжением до определённого его значения (порога ограничения), после чего выходное напряжение остаётся постоянным или равным нулю. Существуют три вида ограничения: ограничение по максимуму (ограничение сверху); ограничение по минимуму (ограничение снизу); двустороннее ограничение (одновременное ограничение сверху и снизу).
Слайд 94: Ограничители амплитуды
Верхним порогом ограничения называется предельный уровень входного напряжения, выше которого выходное напряжение практически не зависит от входного. Основным назначением ограничителей является изменение формы подводимого к ним входного напряжения путём «срезания» части этого напряжения. Следовательно, при ограничении происходит изменение спектрального состава входного напряжения, что возможно лишь при применении нелинейных цепей.
Слайд 95: Ограничители амплитуды
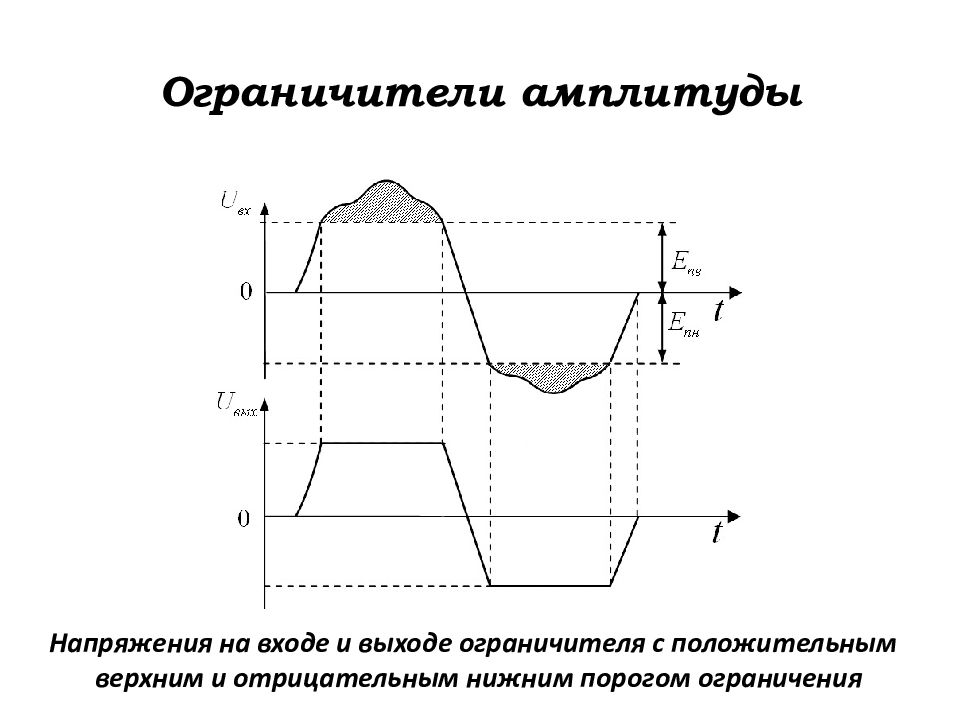
Напряжения на входе и выходе ограничителя с положительным верхним и отрицательным нижним порогом ограничения
Слайд 96: Ограничители амплитуды
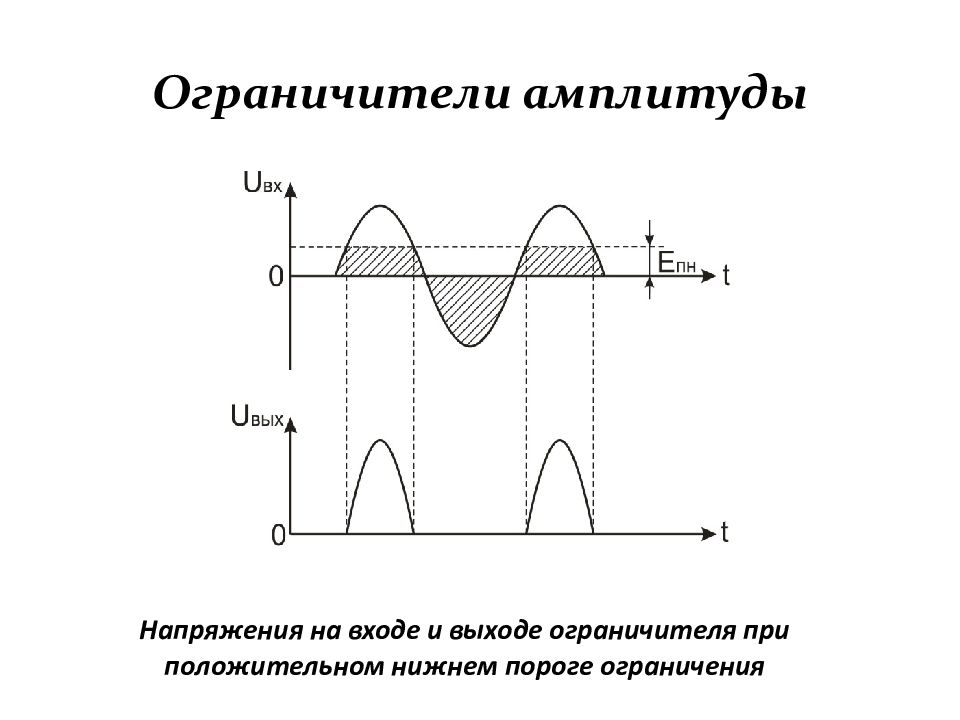
Напряжения на входе и выходе ограничителя пр и положительном нижнем пороге ограничения
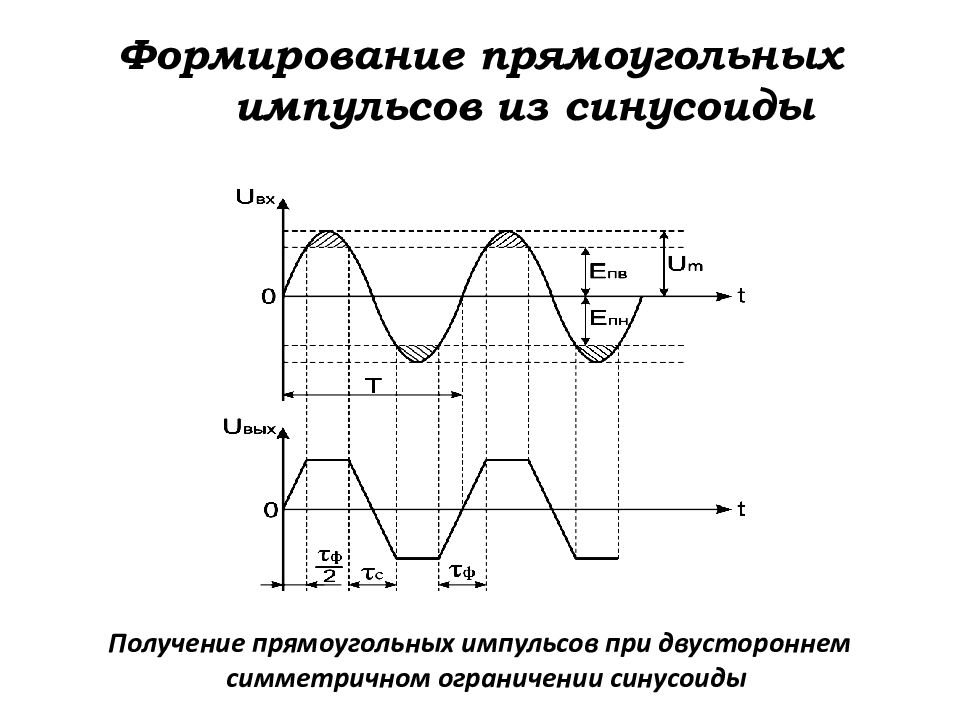
Слайд 97: Формирование прямоугольных импульсов из синусоиды
Получение прямоугольных импульсов при двустороннем симметричном ограничении синусоиды
Слайд 98: Формирование прямоугольных импульсов из синусоиды
Пусть на вход двустороннего амплитудного ограничителя подаётся синусоидальное напряжение Поскольку ограничитель двусторонний симметричный, то Е пв = Е пн = Е п. Напряжение на выходе будет определяться как и, следовательно, ,
Слайд 99: Формирование прямоугольных импульсов из синусоиды
Тогда . После преобразований получим : Если учесть, что т.е. и, следовательно, то можно функцию синуса заменить его аргументом. В результате получим:
Слайд 100: Формирование прямоугольных импульсов из синусоиды
Из этого выражения следует, что формируемое напряжение будет тем ближе к прямоугольной форме, чем больше будет амплитуда синусоиды, чем больше её частота и чем меньше будет порог ограничения. В зависимости от способа включения диода и нагрузки различают два вида ограничителей: диодные ограничители с последовательным включением диода и нагрузки; диодные ограничители с параллельным включением диода и нагрузки.
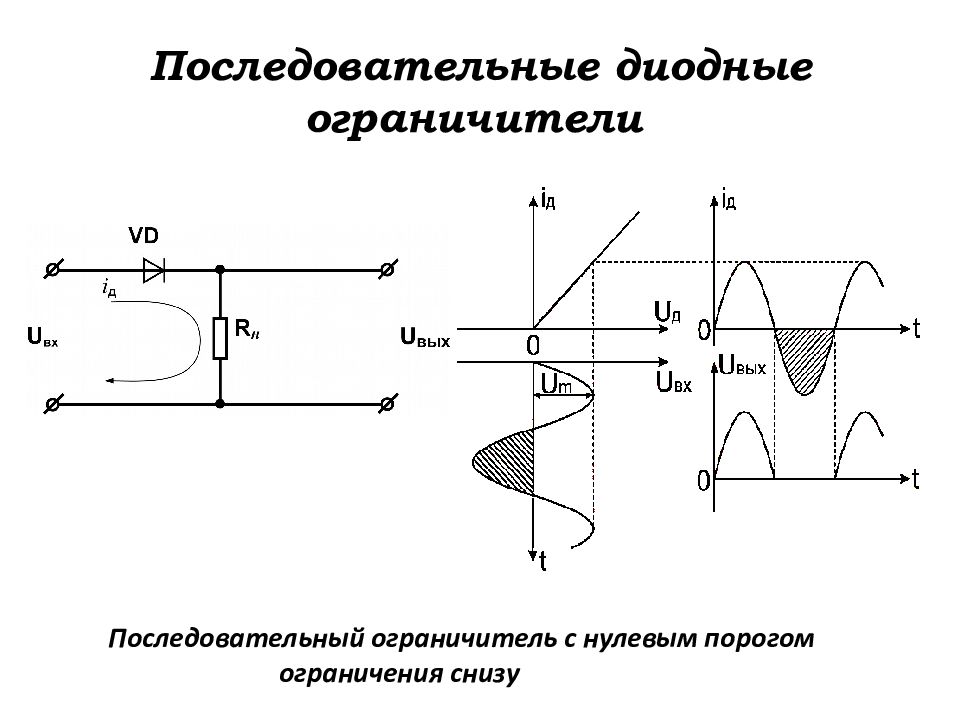
Слайд 101: Последовательные диодные ограничители
Последовательный ограничитель с нулевым порогом ограничения снизу
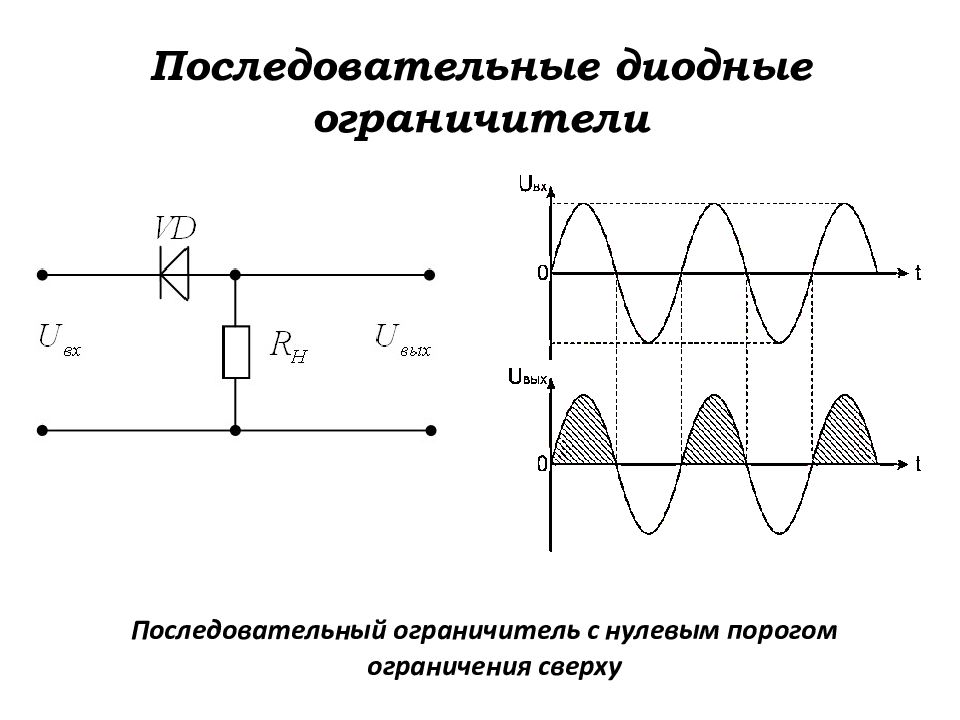
Слайд 102: Последовательные диодные ограничители
Последовательный ограничитель с нулевым порогом ограничения сверху
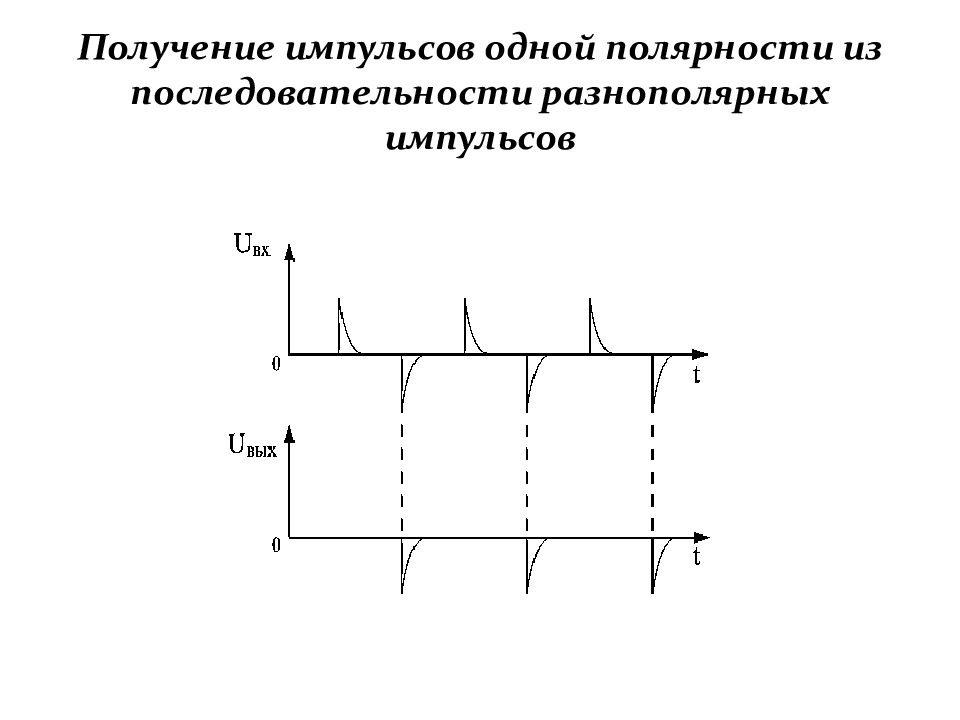
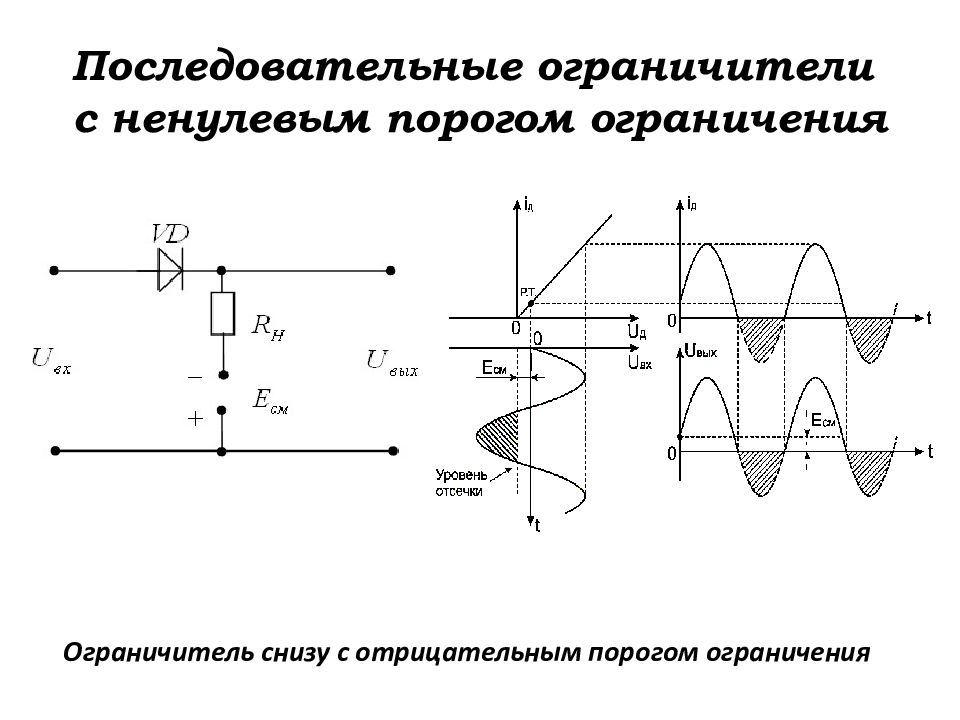
Слайд 103: Получение импульсов одной полярности из последовательности разнополярных импульсов
Ограничитель снизу с отрицательным порогом ограничения
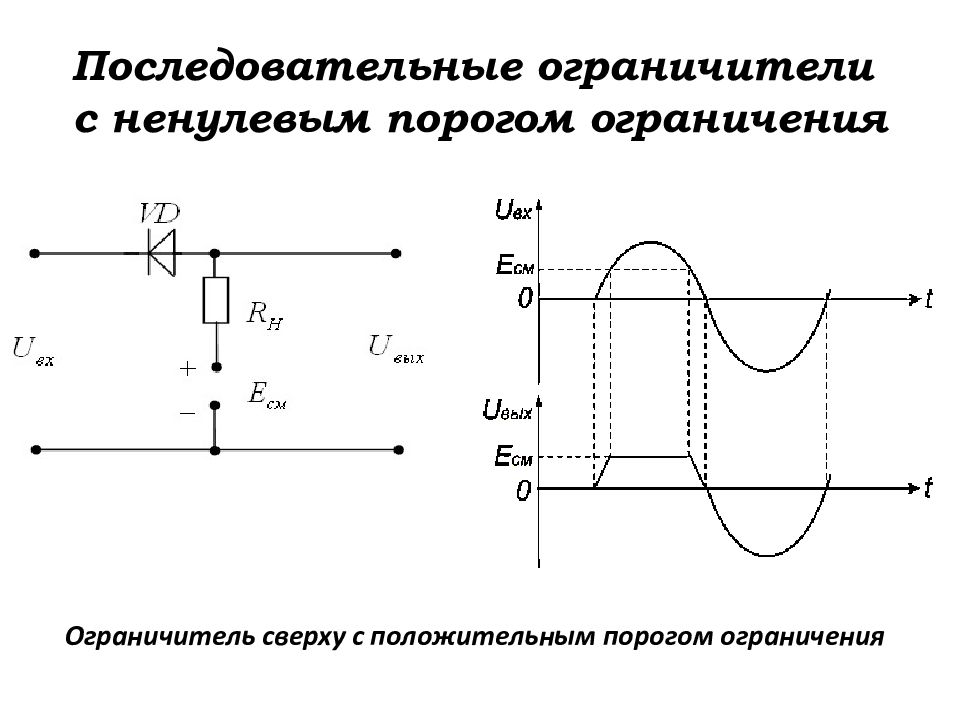
Слайд 105: Последовательные ограничители с ненулевым порогом ограничения
Ограничитель сверху с положительным порогом ограничения
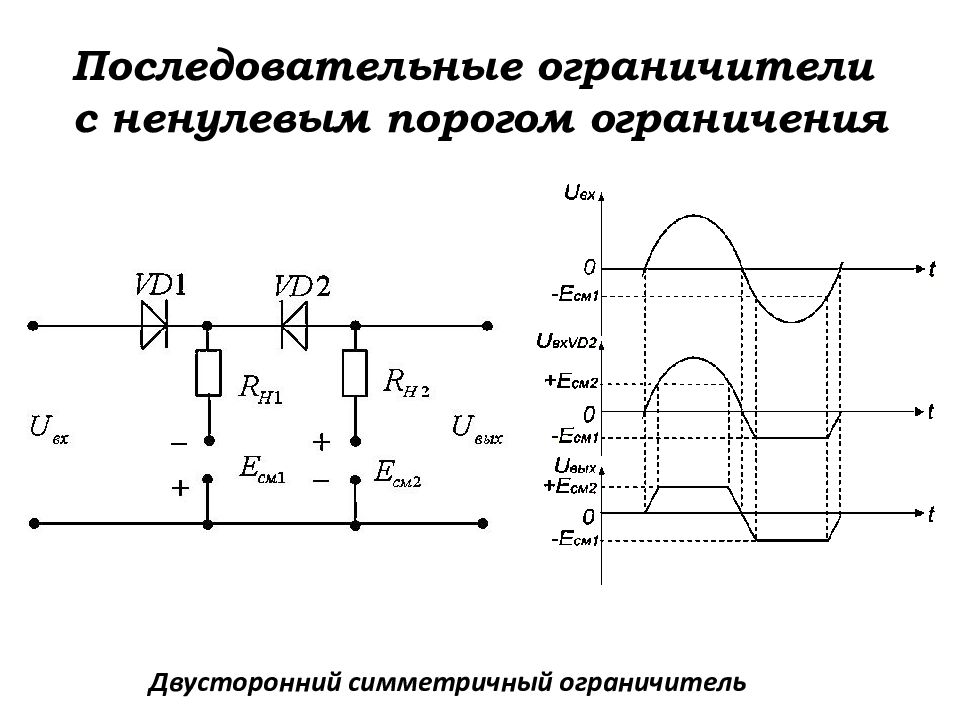
Слайд 106: Последовательные ограничители с ненулевым порогом ограничения
Двусторонний симметричный ограничитель
Слайд 107: Параллельные ограничители
Необходимым элементом схемы параллельных ограничителей является ограничивающий резистор R огр, который выбирается из условия: R обр >> R н >> R огр >> R пр, где R пр и R обр – сопротивления диода, смещённого в прямом и обратном направлениях соответственно.
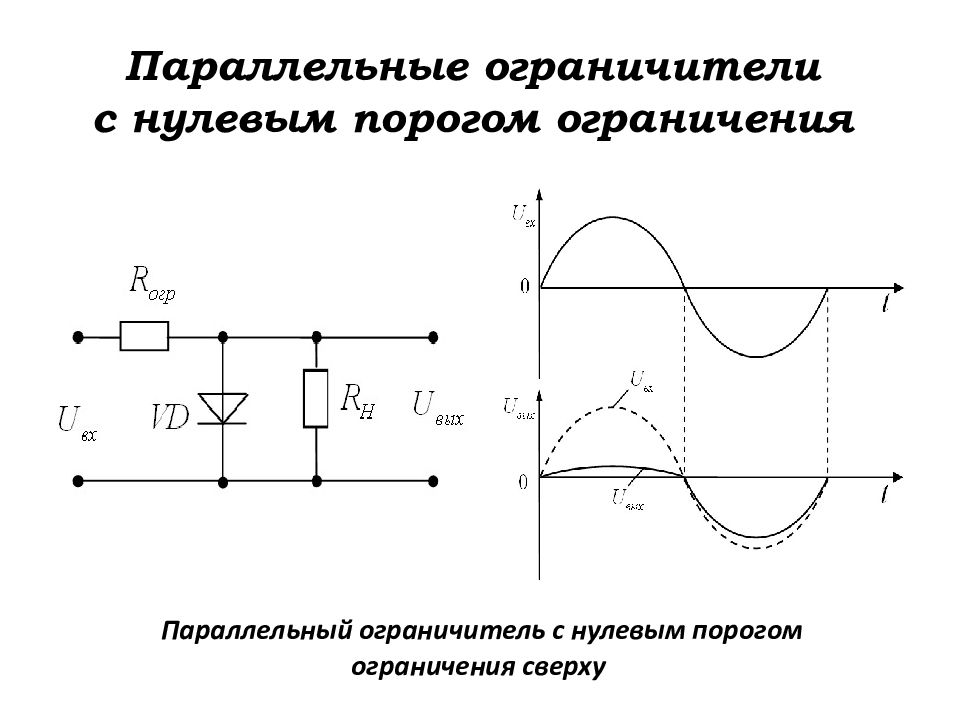
Слайд 108: Параллельные ограничители с нулевым порогом ограничения
Параллельный ограничитель с нулевым порогом ограничения сверху
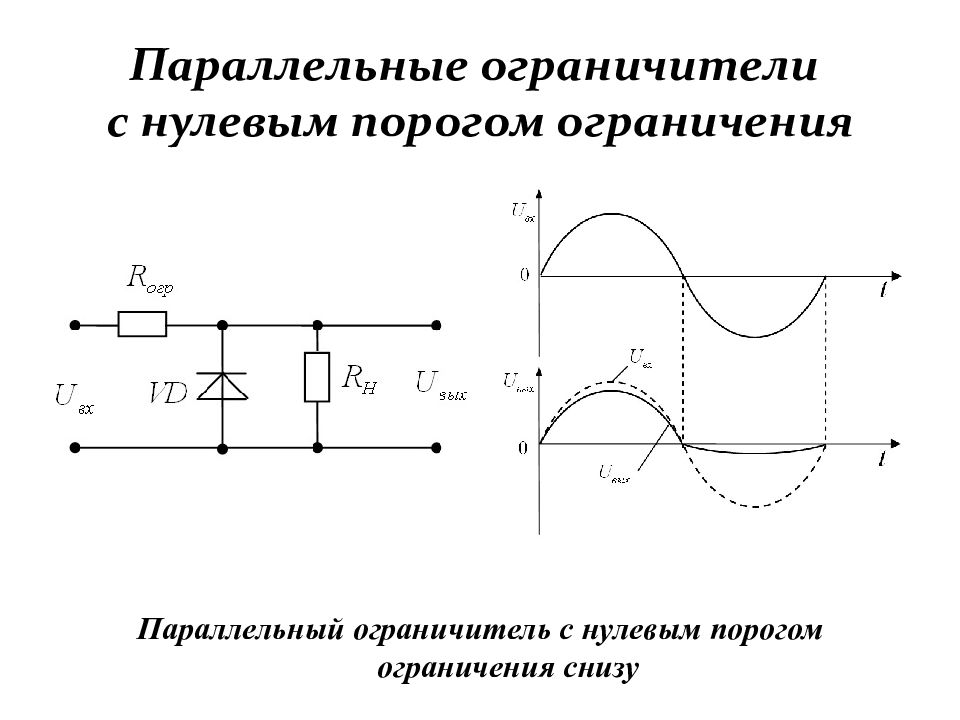
Слайд 109: Параллельные ограничители с нулевым порогом ограничения
Параллельный ограничитель с нулевым порогом ограничения снизу
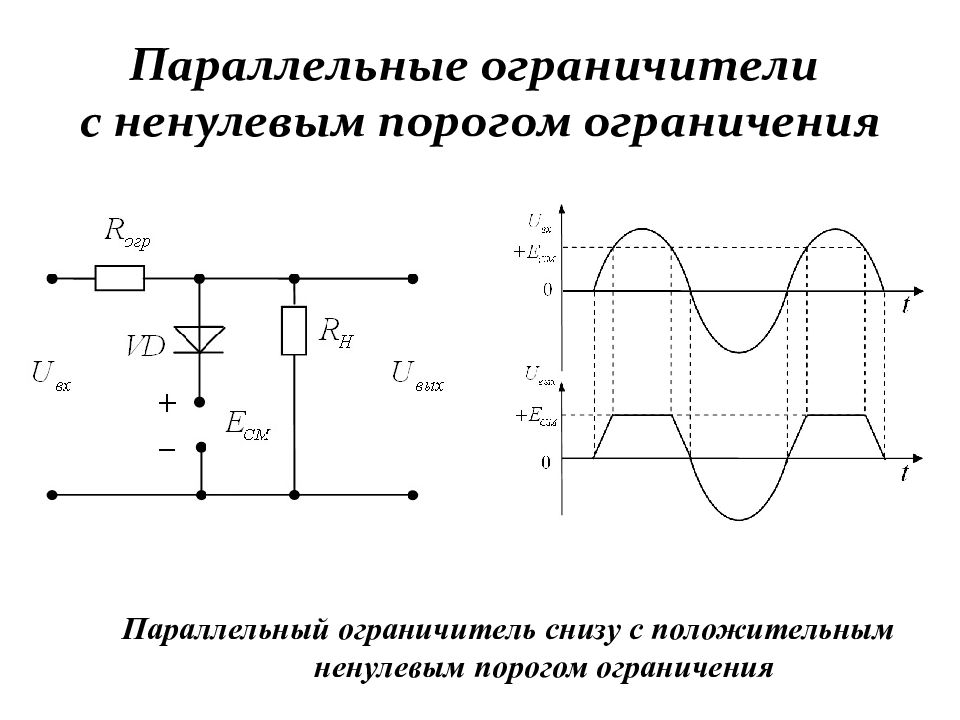
Слайд 110: Параллельные ограничители с ненулевым порогом ограничения
Параллельный ограничитель снизу с положительным ненулевым порогом ограничения
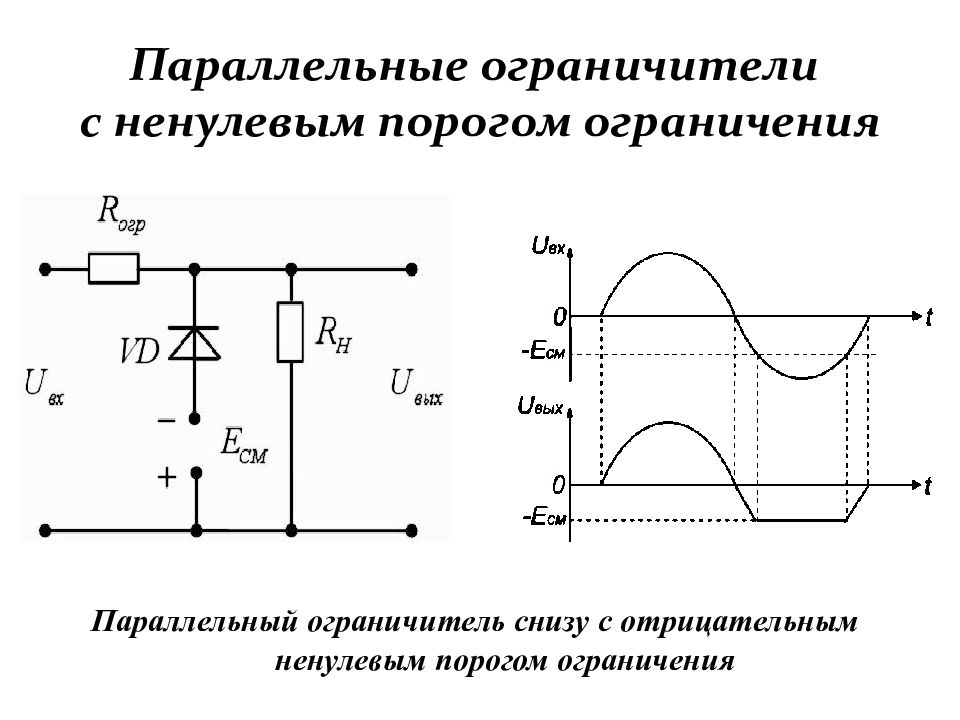
Слайд 111: Параллельные ограничители с ненулевым порогом ограничения
Параллельный ограничитель снизу с отрицательным ненулевым порогом ограничения
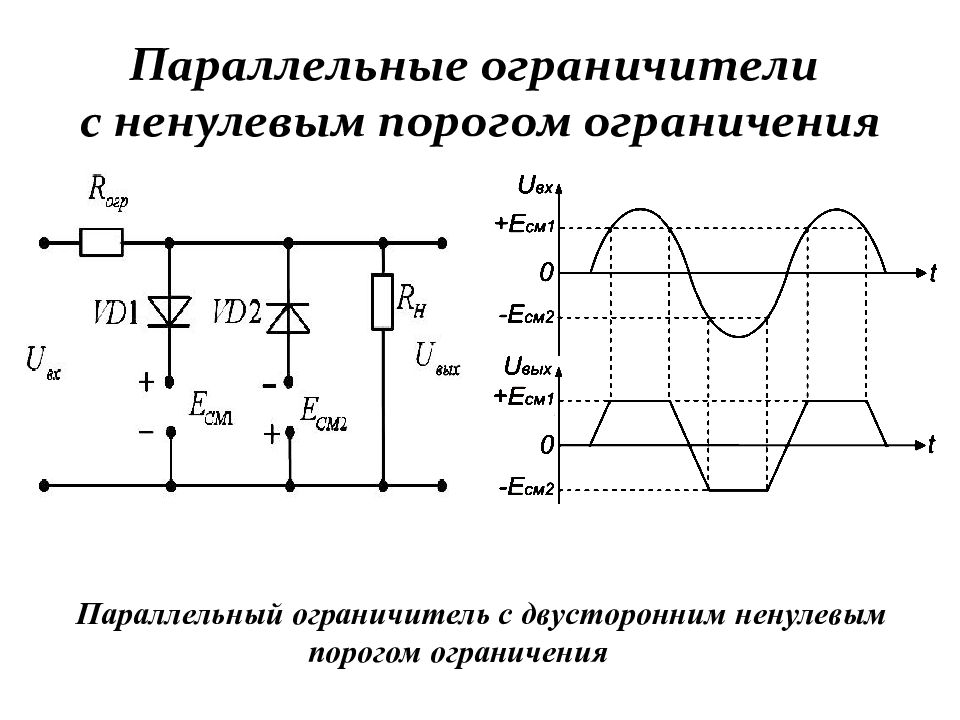
Слайд 112: Параллельные ограничители с ненулевым порогом ограничения
Параллельный ограничитель с двусторонним ненулевым порогом ограничения
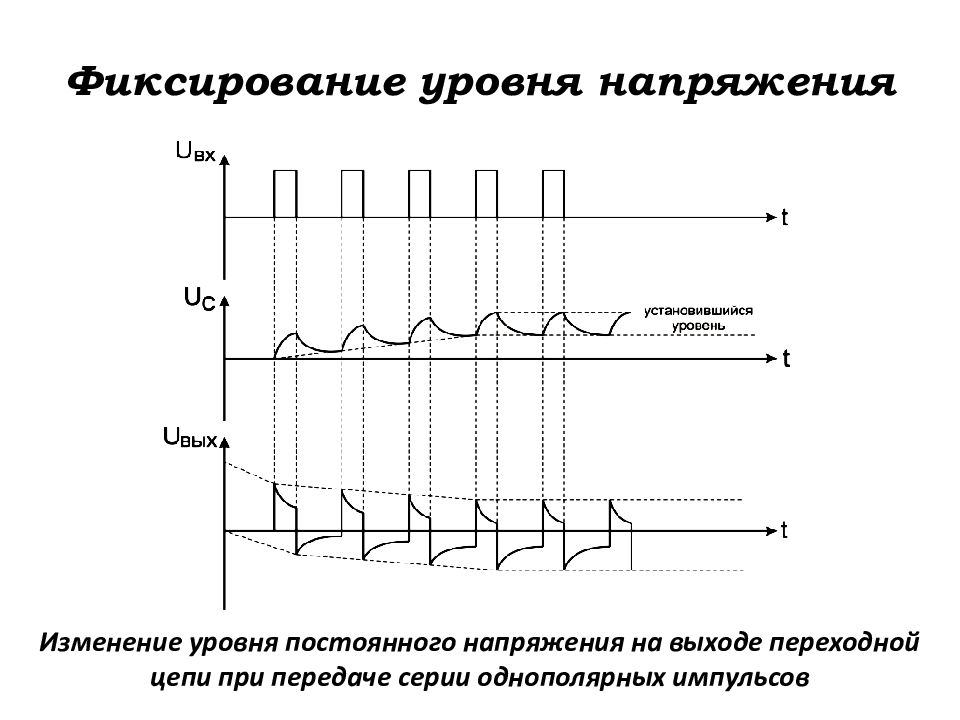
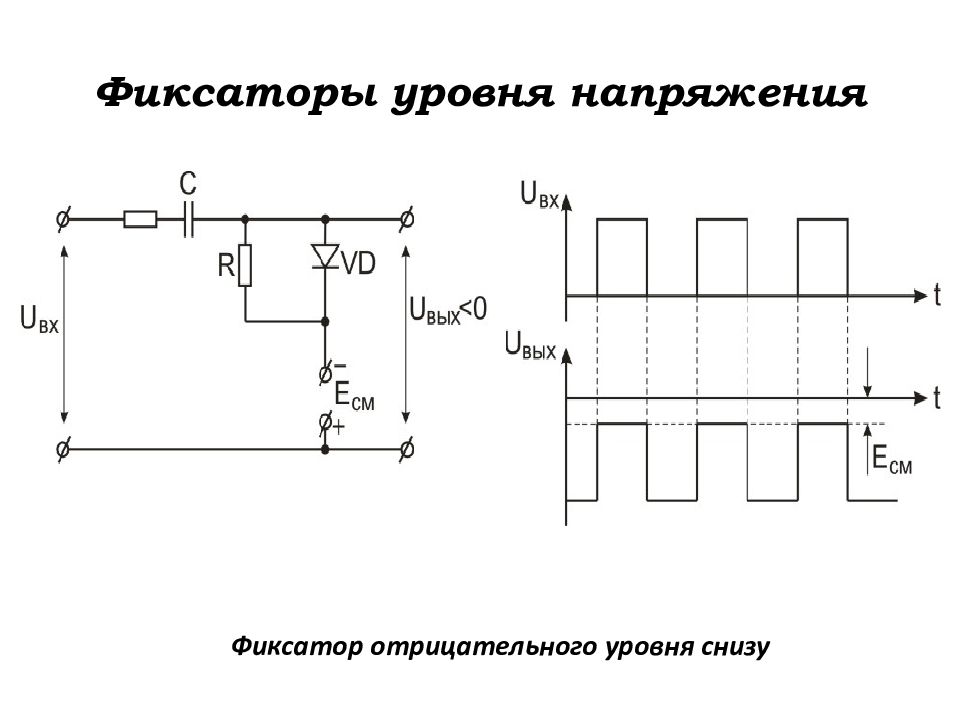
Слайд 114: Фиксирование уровня напряжения
Изменение уровня постоянного напряжения на выходе переходной цепи при передаче серии однополярных импульсов
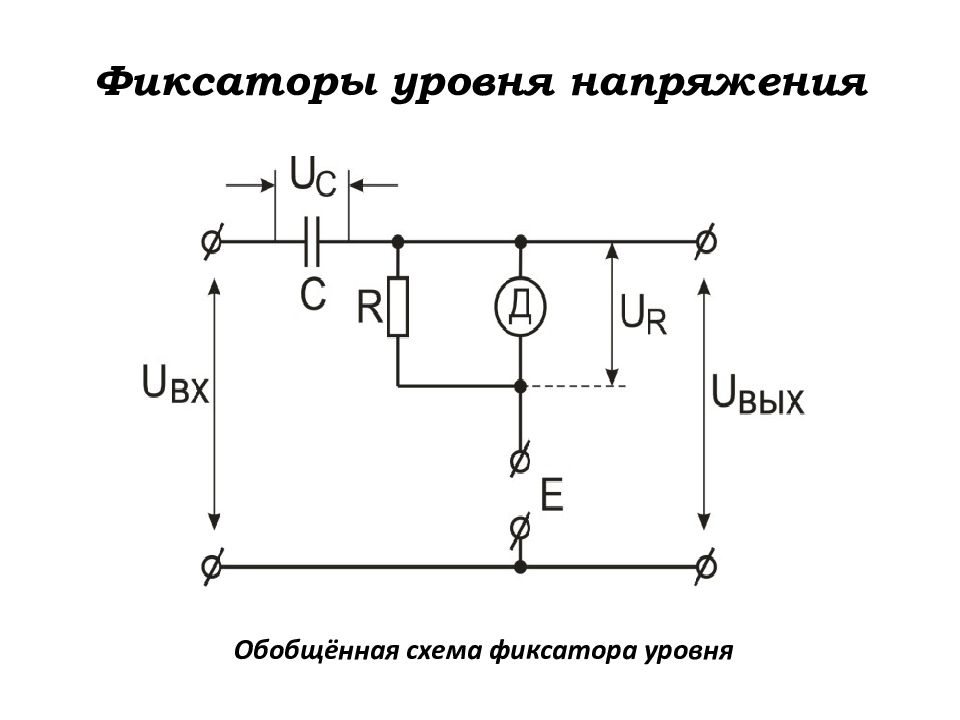
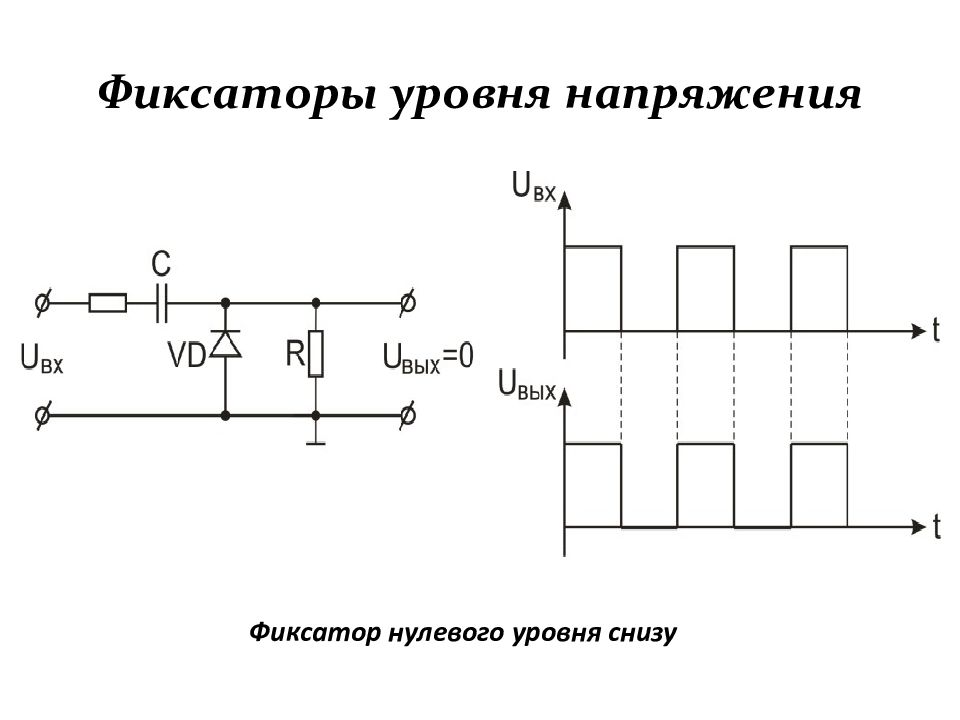
Слайд 115: Фиксаторы уровня напряжения
Фиксаторы уровня обеспечивают постоянный заданный уровень напряжения на выходе переходной цепи независимо от любых изменений параметров импульсов на её входе в любой момент времени. Влияние фиксатора уровня на работу схемы сводятся к резкому уменьшению постоянной времени цепи заряда или разряда переходного конденсатора, вследствие чего уже задолго до прихода очередного импульса в схеме устанавливается необходимый исход-ный режим. Чаще всего используются диодные фиксаторы. Диод, в зависимости от способа включения, уменьшает постоян-ную времени цепи заряда или разряда переходного конденсатора.
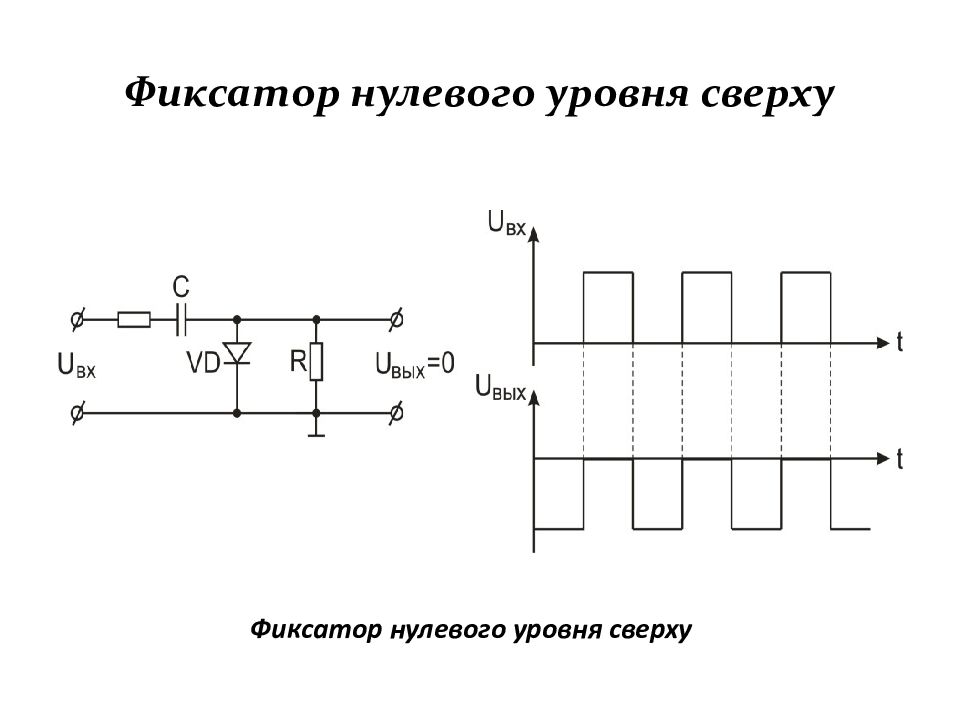
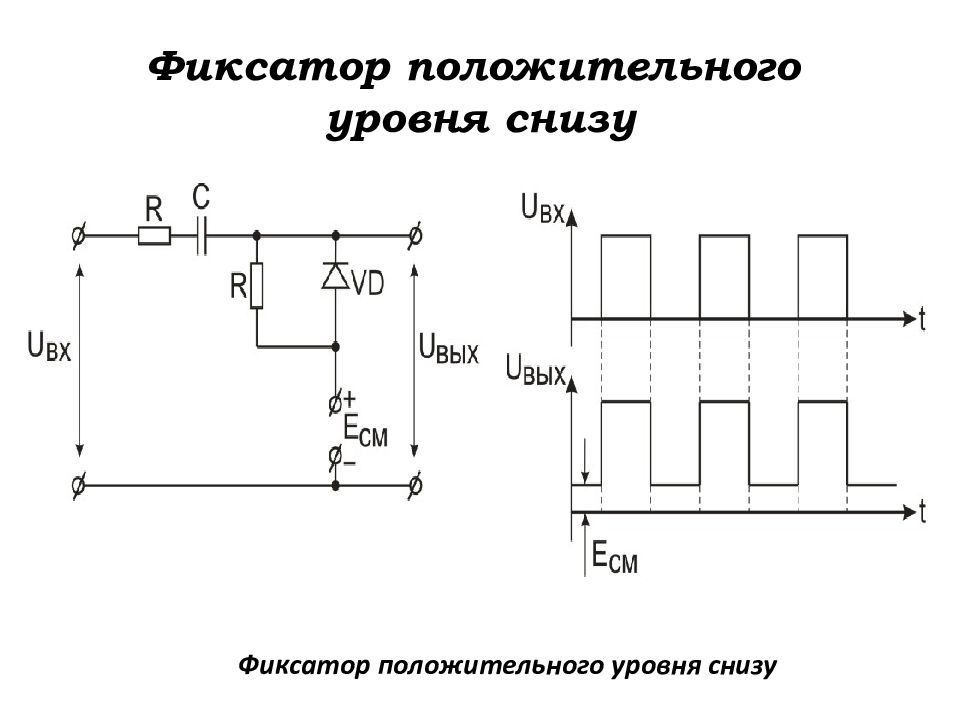
Слайд 122: Фиксатор положительного уровня снизу
Фиксатор положительного уровня снизу
Слайд 123: Фиксатор положительного уровня снизу
до напряжения Если изменить полярность источника смещения и диода, то получим схему фиксатора отрицательного уровня снизу.
Слайд 126: Релаксационные колебания
Колебания, в которых медленные изменения напряжения чередуются со скачкообразными, называются релаксационными. Релаксационным называют генератор, вырабатывающий негармонические электрические колебания (импульсы) в результате быстрого высвобождения энергии, запасённой от источника постоянного тока.
Слайд 127: Условия возникновения релаксационных колебаний:
Наличие глубокой положительной обратной связи Баланс амплитуд Баланс фаз Только при этом условии возможны скачки напряжения и тока. Это условие реализуется, если коэффициент усиления усилительного элемента будет больше единицы. Это условие реализуется, если с выхода усилительного элемента на его вход будет подаваться сигнал с фазой, равной фазе входного сигнала, что возможно только при наличии положительной обратной связи.
Слайд 128: Релаксационные генераторы
Релаксационные генераторы могут работать в трёх режимах: Автоколебательном; Ждущем (режим внешнего запуска); Автоколебательном с внешней синхронизацией Кроме того, релаксационные генераторы могут работать в режиме деления частоты (разновидность режима синхронизации). К релаксационным генераторам относятся генераторы прямоугольных и пилообразных импульсов. Прямоугольные импульсы вырабатывают мультивибраторы, спусковые схемы, триггеры и блокинг-генераторы.
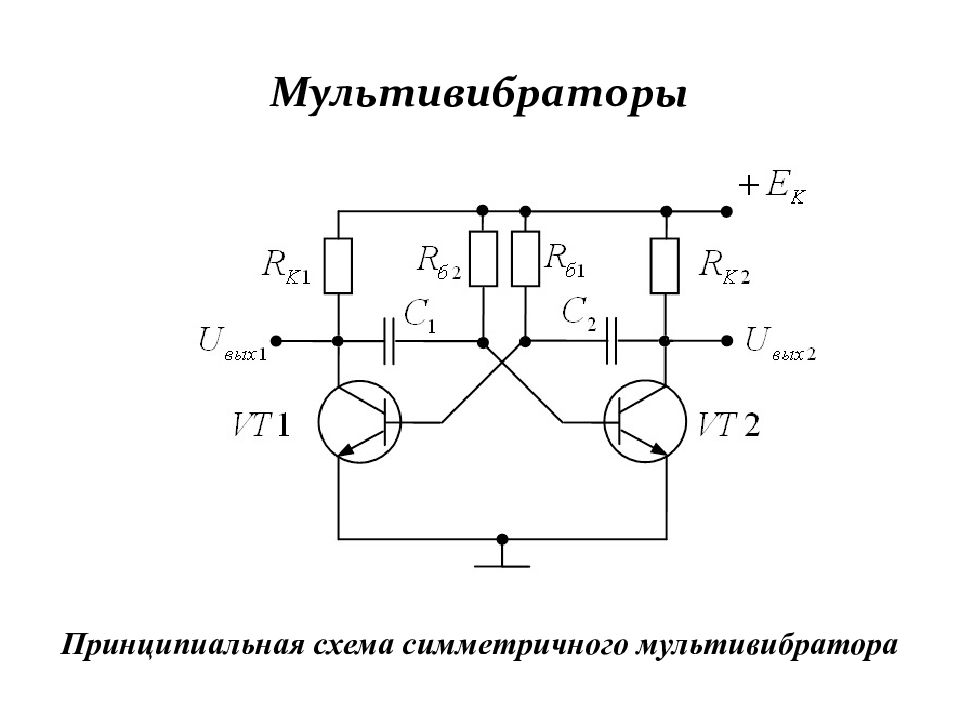
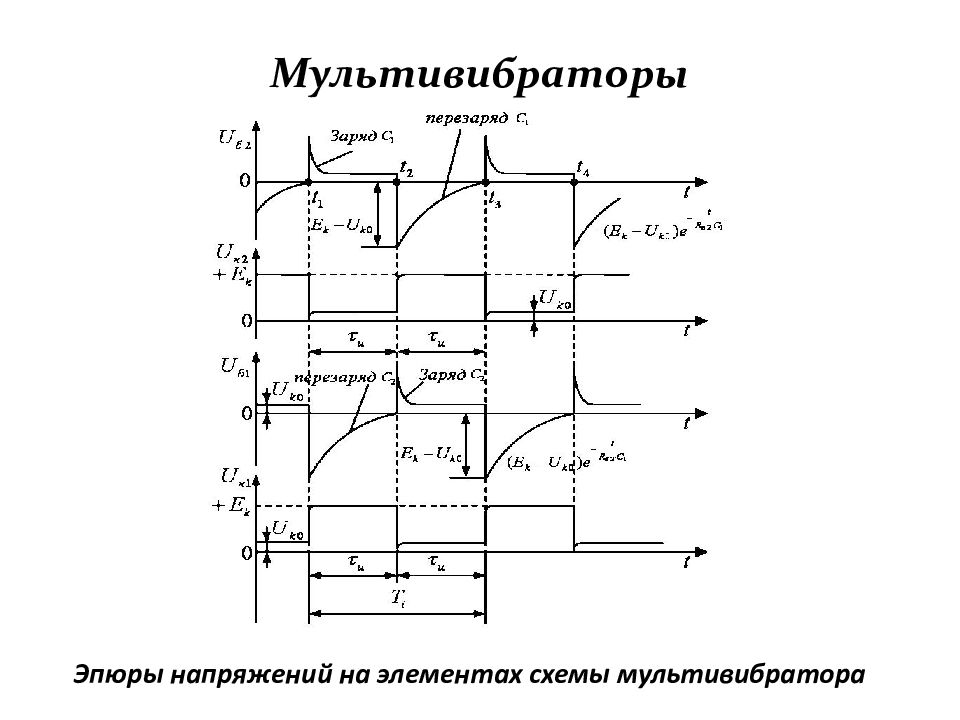
Слайд 129: Мультивибраторы
По схеме мультивибратор представляет собой двухкаскадный апериодический усилитель с глубокой положительной обратной связью, у которого выход первого каскада связан с входом второго и наоборот. Такое соединение каскадов создаёт условия для возникновения релаксационных колебаний, т.к. при этом выполняются все три условия их возникновения.
Слайд 130: Условия самовозбуждения симметричного мультивибратора
Глубокая положительная обратная связь. Это условие реализует требование баланса фаз в автогенераторе.
Слайд 133: Мультивибраторы
Первое опрокидывание схемы ( t = t 1 ) : + Δ i к 2 → – Δ U к 2 → – Δ U б 1 → – Δ i б 1 → – Δ i к 1 → + Δ U к 1 → →+ Δ U б 2 → + Δ i' к 2 > + Δ i к 2 2. t 1 < t < t 2 Заряд C 1 происходит по цепи: + Е к → R к 1 → C 1 → (Б – Э)VT 2 → корпус ( – Е к ). Разряд C 2 происходит по цепи : + C 2 → (К – Э)VT 2 → корпус ( –Е к ) → +Е к → R б 1 → –C 2 Падение напряжения на R б 1 уменьшается по закону:
Слайд 134: Мультивибраторы
3. Второй скачок (обратное опрокидывание схемы), t = t 2 : + Δ i к 1 → – Δ U к 1 → – Δ U б 2 → – Δ i к 2 → + Δ U к 2 → + Δ U б 2 → → + Δ i ' к 1 > + Δ i к 1. 4. Восстановление исходного состояния схемы, t 2 < t < t 3 : – разряд конденсатора C 1 происходит по цепи: +C 1 → (К – Э)VT 1 → ко рпус → +Е к → R б 2 → – C 1 – заряд конденсатора C 2 происходит по цепи : +Е к → R к 2 → C 2 → (Б – Э) VT 1 → корпус ( –Е к )
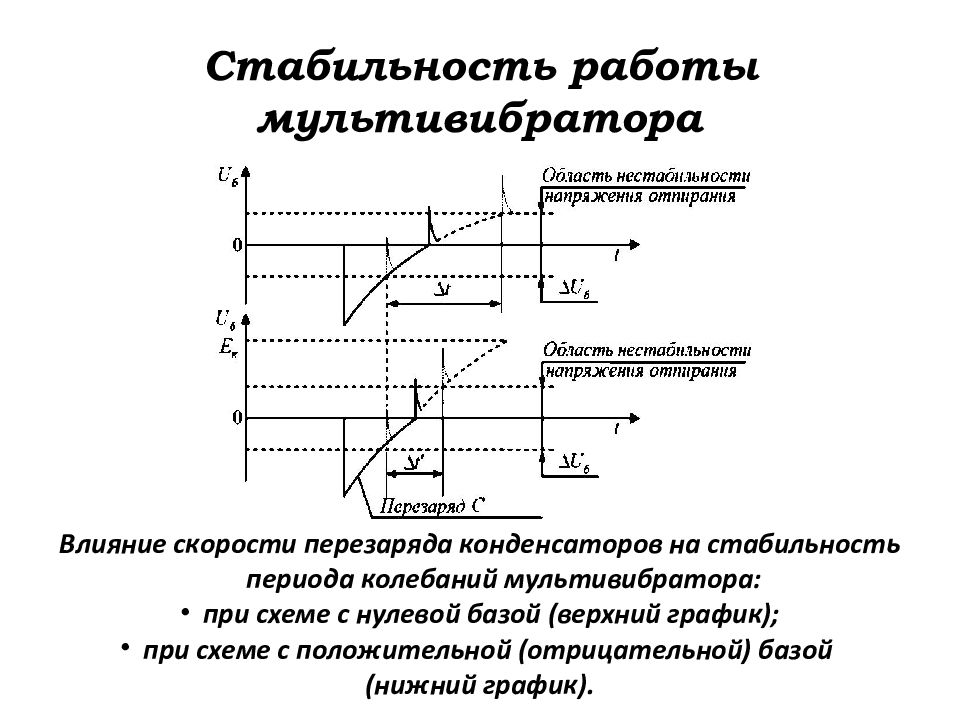
Слайд 135: Стабильность работы мультивибратора
Влияние скорости перезаряда конденсаторов на стабильность периода колебаний мультивибратора: при схеме с нулевой базой (верхний график); при схеме с положительной (отрицательной) базой (нижний график).
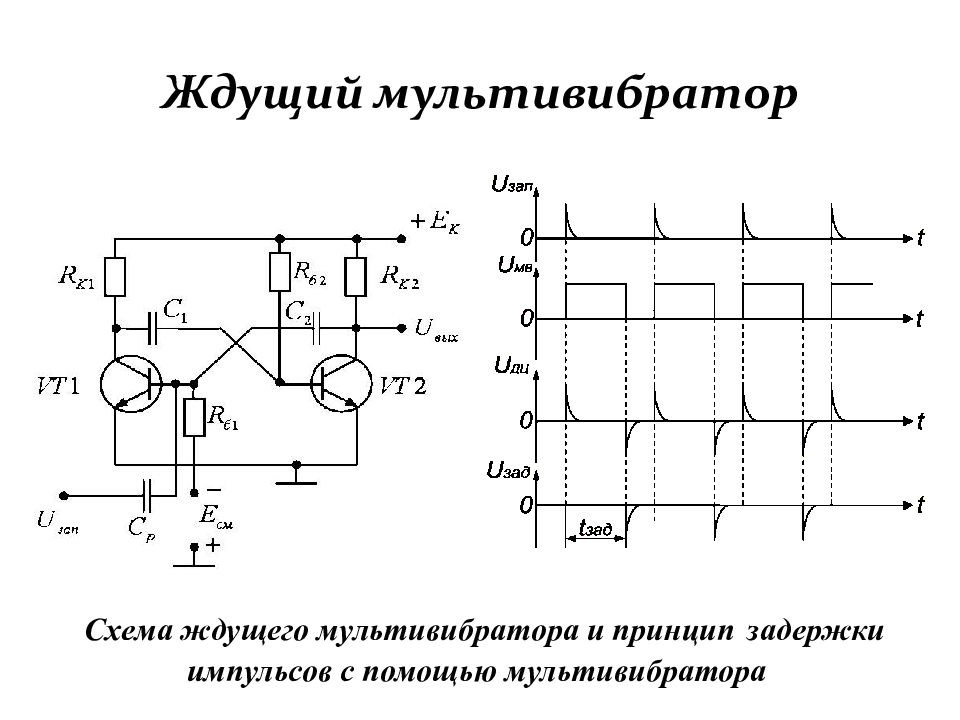
Слайд 136: Ждущий мультивибратор
Схема ждущего мультивибратора и принцип задержки импульсов с помощью мультивибратора
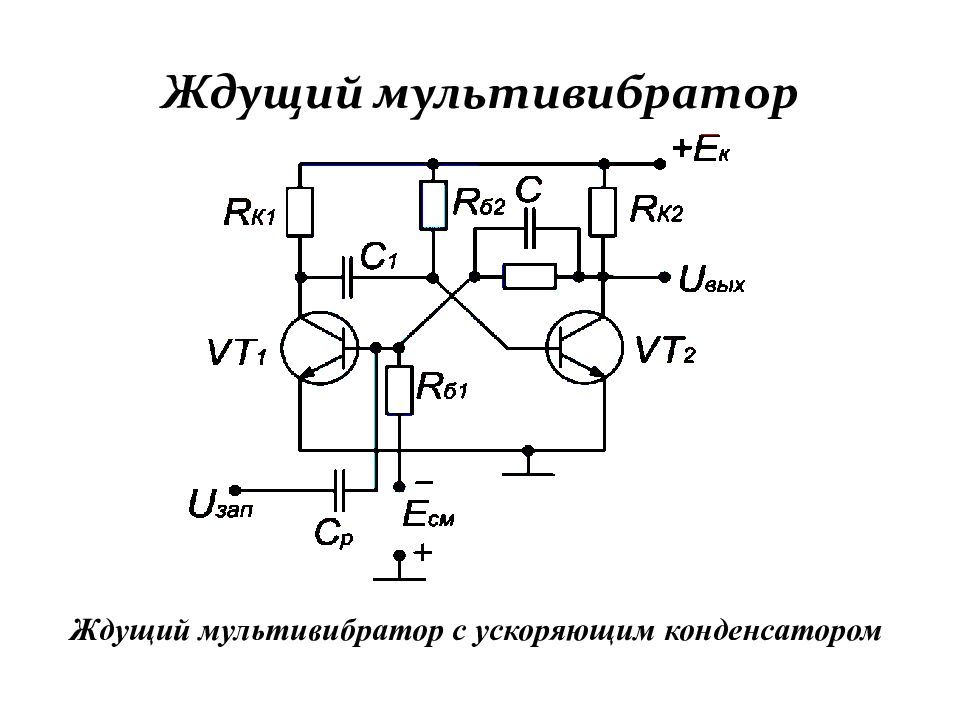
Слайд 137: Ждущий мультивибратор
Ждущий мультивибратор с ускоряющим конденсатором
Слайд 138: Генераторы импульсов с внешним запуском (спусковые схемы)
Схемы таких генераторов иногда называют спусковыми. По количеству устойчивых состояний равновесия все спусковые схемы можно разделить на два класса: схемы с одним устойчивым состоянием равновесия. Эти схемы в своём составе обязательно имеют реактивный элемент (чаще всего это ёмкость). Такие схемы называют одновибраторами. схемы с двумя устойчивыми состояниями равновесия. Такие схемы в своём составе могут иметь только активные элементы и называются триггерами.
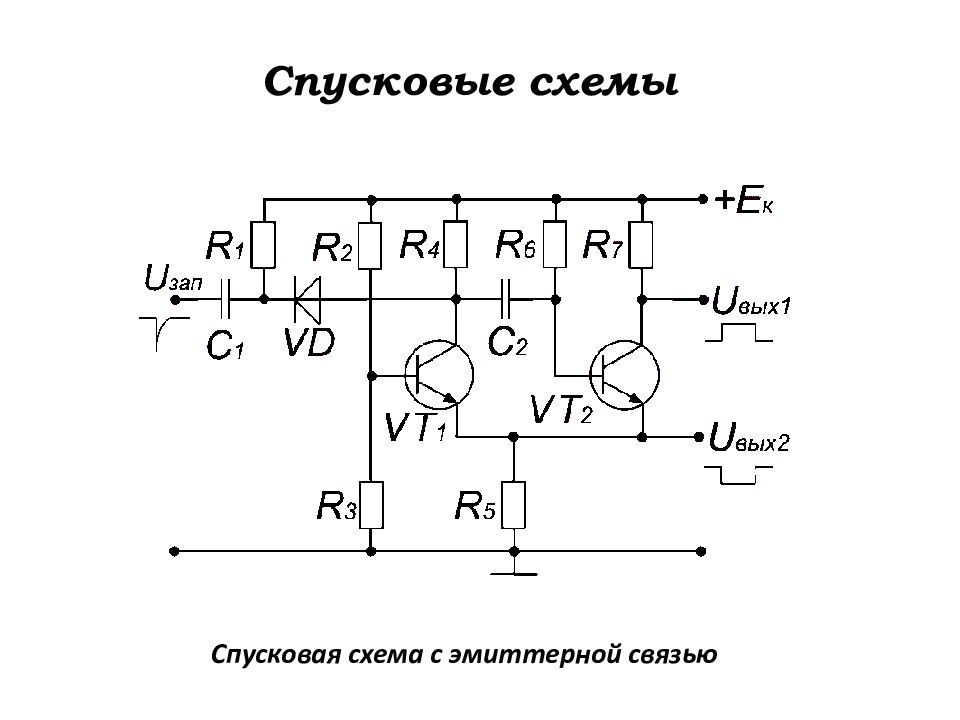
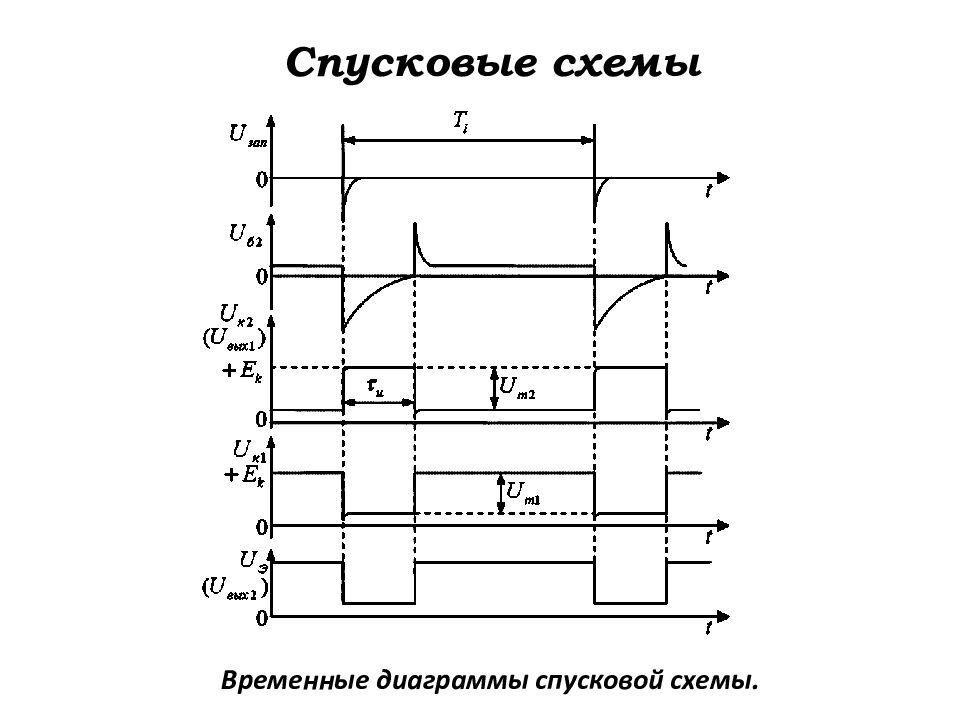
Слайд 141: Работа спусковой схемы
1. Исходное состояние В исходном состоянии транзистор VT 2 открыт, т.к. на его базу подаётся положительное напряжение + Е к через резистор R 6. Транзистор VT 2 закрыт. Конденсатор C 2 заряжен по цепи: + Е к → R 4 → C 2 → (Б-Э) VT 2 → R 5 → корпус (–Е к ).
Слайд 142: Работа спусковой схемы
2. Запуск и опрокидывание схемы. Транзистор VT 2 запирается и возникает лавинообразный процесс: – U вх → – Δ U б2 → – Δ i б2 → – Δ i к2 → – Δ U э → + Δ U б1 → + Δ i к1 → → – Δ U к1 → – Δ U ' б2 > – Δ U б2, при котором замыкается цепь положительной обратной связи. В результате появления лавинообразного процесса VT 2 запирается, а VT 1 полностью отпирается и насыщается. Происходит резкое уменьшение напряжения на коллекторе VT 1, в результате чего диод VD запирается и отключает источник импульсов запуска от схемы генератора.
Слайд 143: Работа спусковой схемы
3. Формирование импульса. После отпирания VT 1 конденсатор C 2 начинает разряжаться по цепи: + C 2 (левая обкладка) → (К – Э) VT 1 → R 5 → корпус (–Е к ) → → +Е к → R 6 → – C 2 (правая обкладка).
Слайд 144: Работа спусковой схемы
4. Восстановление исходного состояния схемы. В момент отпирания VT 2 в цепи его коллектора появляется ток, что вновь приводит к возникновению лавинообразного процесса и замыканию цепи положительной обратной связи: + Δ i к2 → + Δ U э → – Δ U б1 → – Δ i к1 → + Δ U к1 → + Δ U б2 → + Δ i ' к2 >+ Δ i к2. Происходит обратное опрокидывание схемы, в результате которого VT 1 запирается, а VT 2 полностью отпирается. Конденсатор C 2 снова начинает заряжаться по цепи: +Е к → R 4 → C 2 → (Б – Э) VT 2 → R 5 → –Е к (корпус).
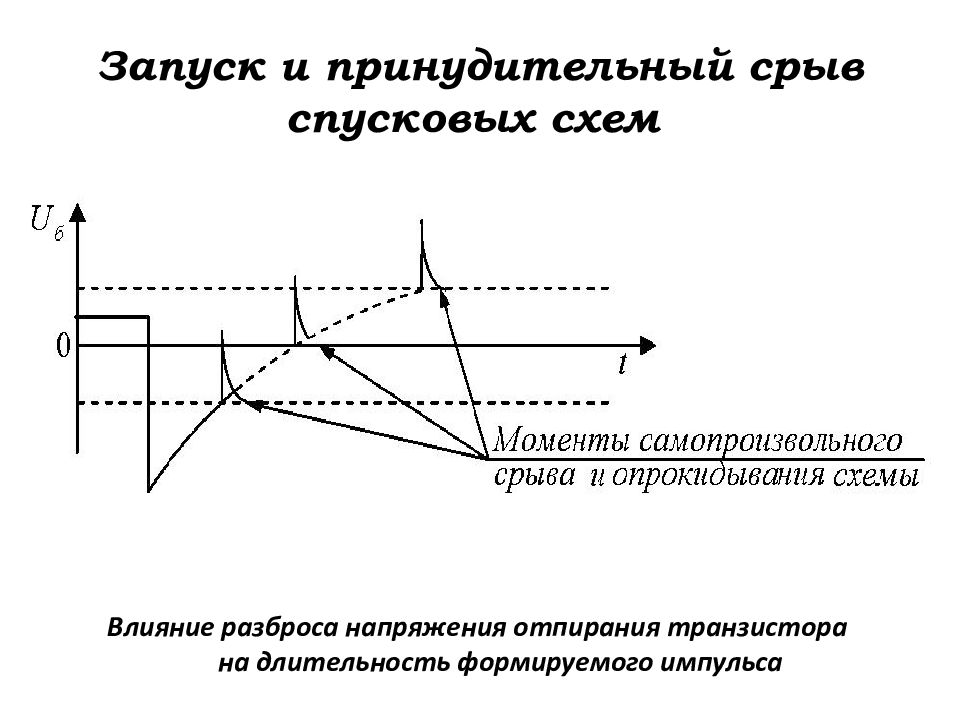
Слайд 145: Запуск и принудительный срыв спусковых схем
Влияние разброса напряжения отпирания транзистора на длительность формируемого импульса
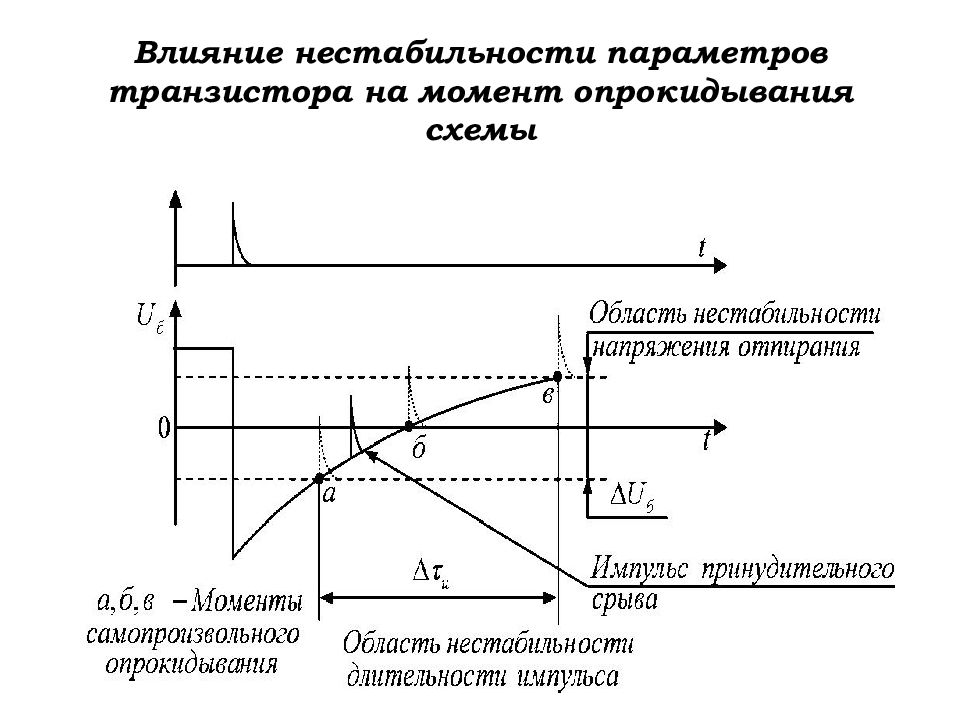
Слайд 146: Влияние нестабильности параметров транзистора на момент опрокидывания схемы
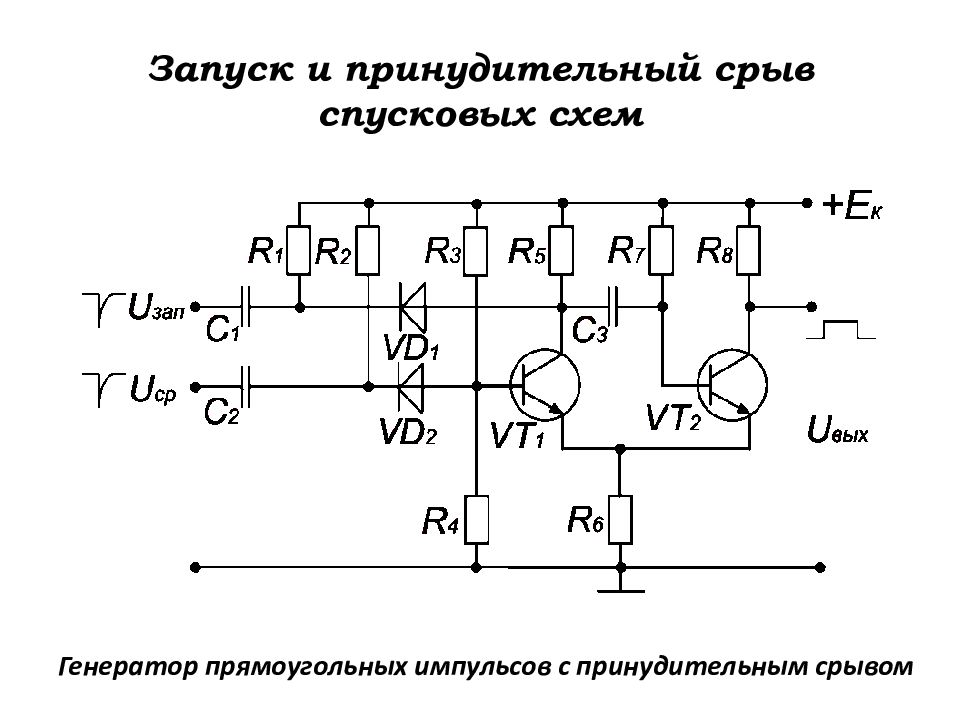
Слайд 147: Запуск и принудительный срыв спусковых схем
Генератор прямоугольных импульсов с принудительным срывом
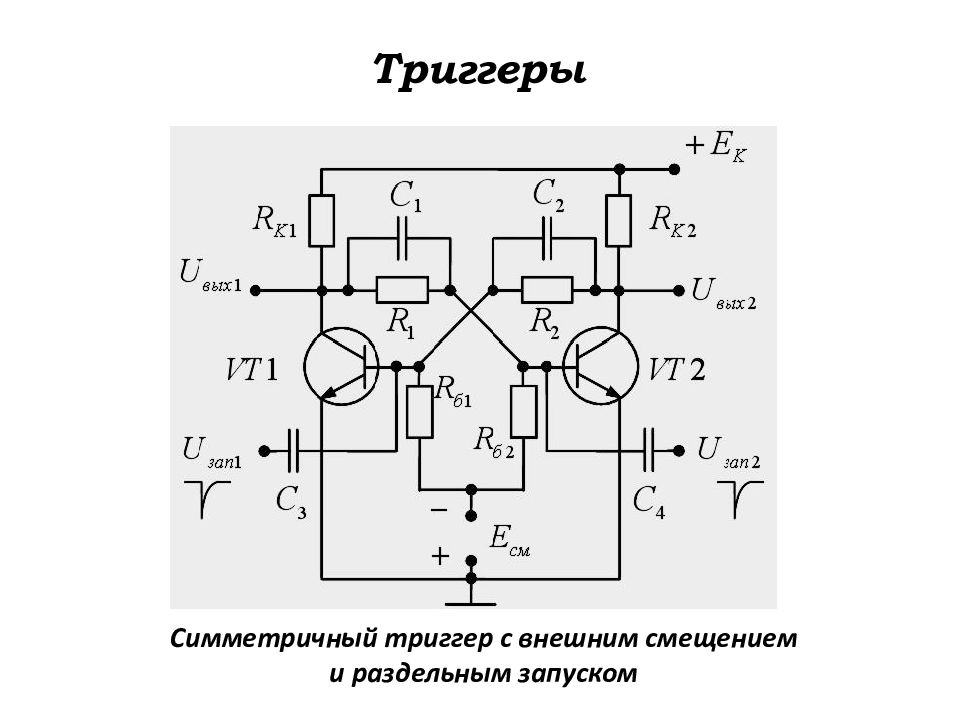
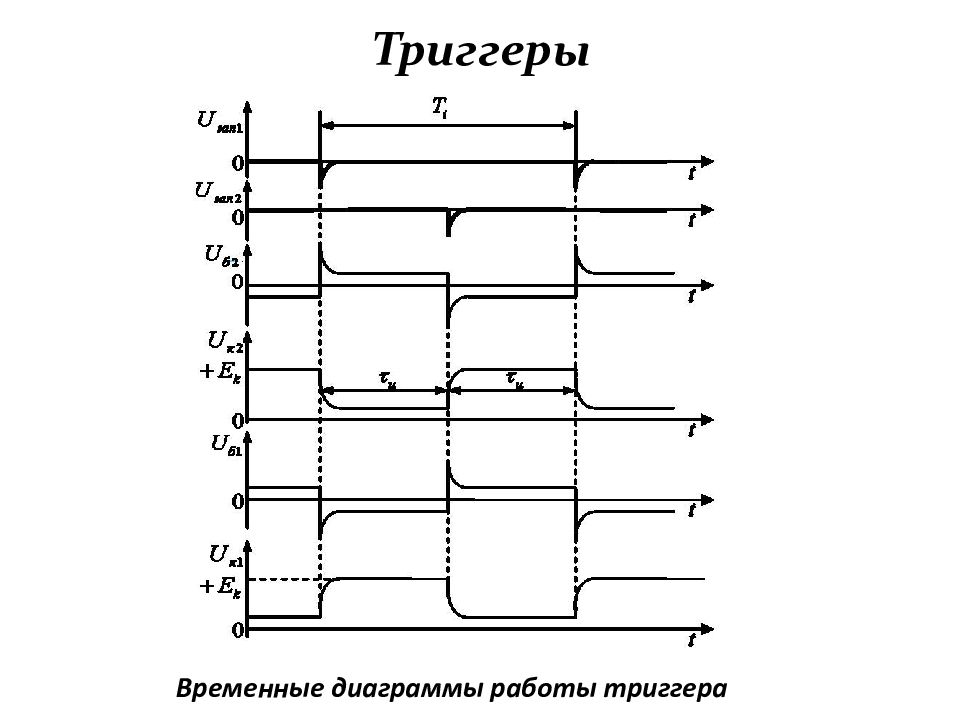
Слайд 148: Триггеры
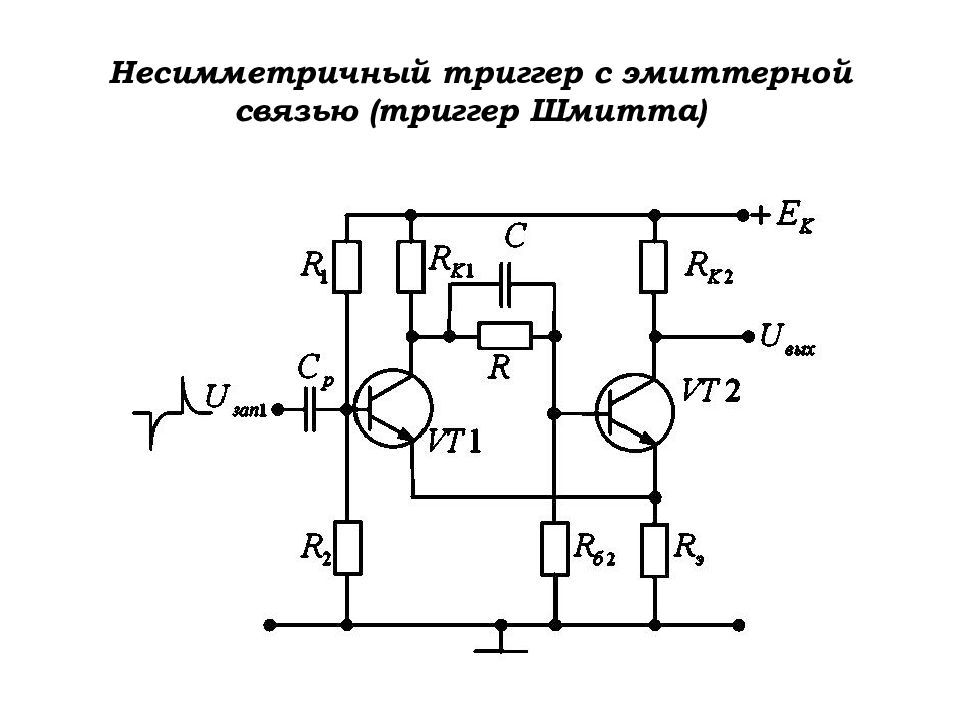
Симметричный триггер с внешним смещением и раздельным запуском
Слайд 152: Работа триггера Шмитта
Введём следующие обозначения: U ' э – уровень напряжения на эмиттерах схемы, при котором происходит отпирание транзистора VT 1 U '' э – уровень напряжения на эмиттерах схемы, при котором происходит отпирание транзистора VT 2 В исходном состоянии открыт и насыщен за счёт напряжения, снимаемого с делителя R 1 – R 2.
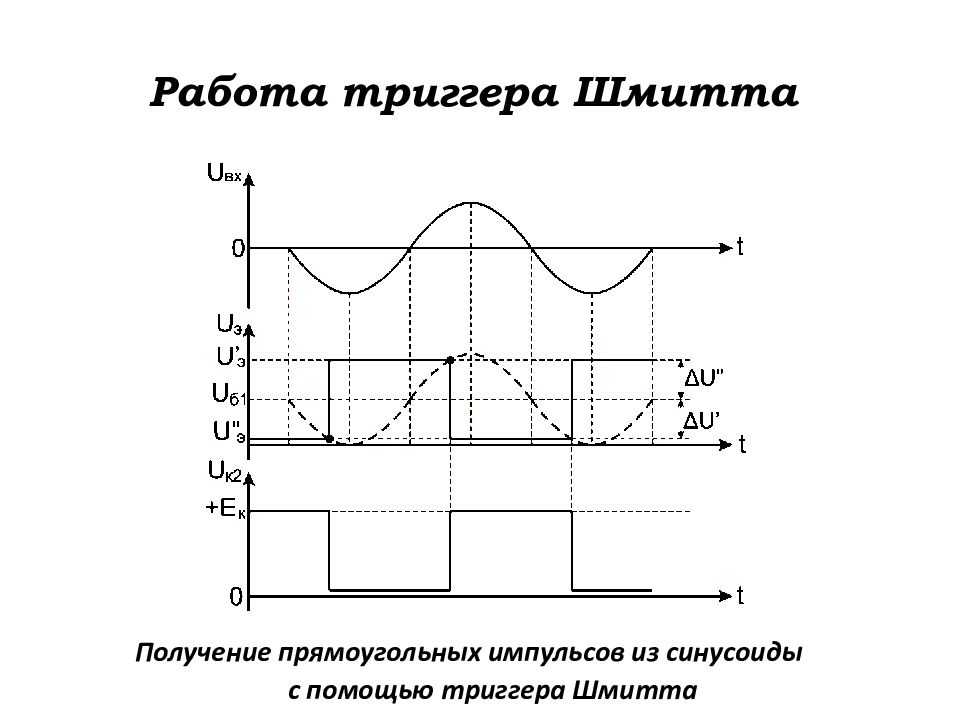
Слайд 153: Работа триггера Шмитта
Получение прямоугольных импульсов из синусоиды с помощью триггера Шмитта
Слайд 154: Работа триггера Шмитта
Пусть на базу открытого транзистора VT 1 подаётся отрицательный запускающий импульс, под действием которого VT 1 выходит из состояния насыщения и потенциал его коллектора становится более положительным. Возникает лавинообразный процесс: + Δ U к1 → + Δ U б2 → + Δ i к2 → + Δ i э2 → + Δ U R э → – Δ U б1 → – Δ i к1 → → + Δ U ' к1 (> + Δ U к1 ).
Слайд 155: Работа триггера Шмитта
В результате лавинообразного процесса транзистор VT 1 запирается, а VT 2 полностью отпирается и насыщается. Аналогично протекает и обратный процесс, когда на вход VT 1 поступает положительный импульс. Триггер Шмитта часто используют для формирования прямоугольных импульсов из напряжения произвольной формы и, в частности, из синусоидального напряжения.
Слайд 156: Работа триггера Шмитта
Как только под действием U вх потенциал базы транзистора VT 1 станет равным потенциалу эмиттера ( U б1 = U '‘ Э ), транзистор VT 1 запирается, схема лавинообразно опрокидывается, и транзистор VT 2 отпирается и насыщается. Пока VT 1 остаётся запертым, на выходе формируется плоская вершина импульса. Когда под действием U вх потенциал базы VT 1 сравняется с новым значением потенциала эмиттера ( U б1 = U ' Э ), начнётся новый лавинообразный процесс, в результате которого будет сформиро-ван срез импульса, после чего схема вернётся в своё исходное состояние. Подбором величин резисторов R 1 и R 2 можно так подобрать режим работы VT 1, что он будет находиться одинаковое время в запертом и открытом состояниях.
Слайд 157: Работа триггера Шмитта
При Δ U ′ = Δ U ′′ триггер может переключаться разнополярными напряжениями одинакового уровня. При этом длительности формирования импульса и паузы будут одинаковыми. При Δ U ′ ≠ Δ U ′′ переключение осуществляется разно-полярными напряжениями разных значений. Благодаря лавинообразным процессам триггер Шмитта, по сравнению с ограничителями амплитуды, обеспечивает лучшую форму прямоугольных импульсов, формируемых из синусоиды. Триггер Шмитта можно использовать как пороговое устройство: если входной сигнал достигает определённого порога, то триггер переключается. Величину порога переключения можно менять, изменяя потенциал базы VT 1 с помощью делителя напряжения R 1 - R 2.
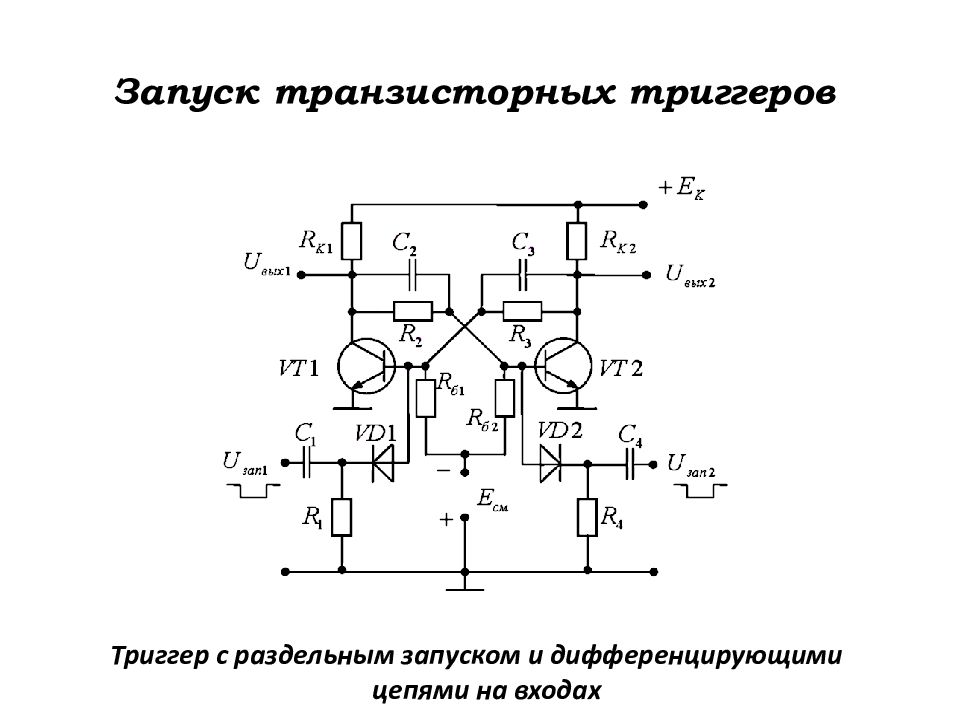
Слайд 158: Запуск транзисторных триггеров
Триггер с раздельным запуском и дифференцирующими цепями на входах
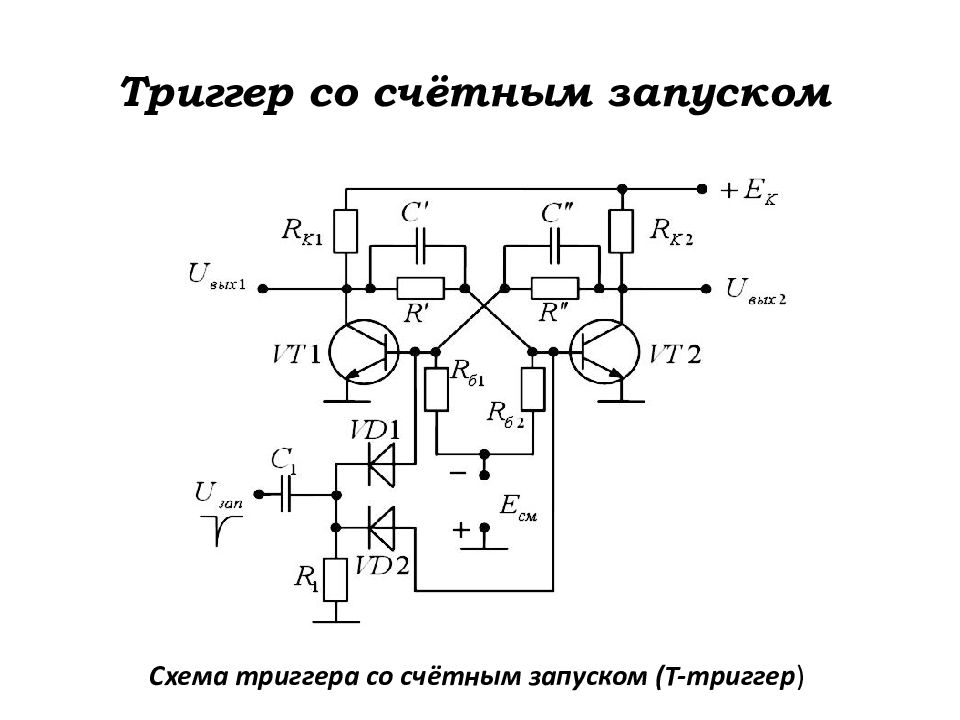
Слайд 159: Триггер со счётным запуском
Схема триггера со счётным запуском (Т-триггер )
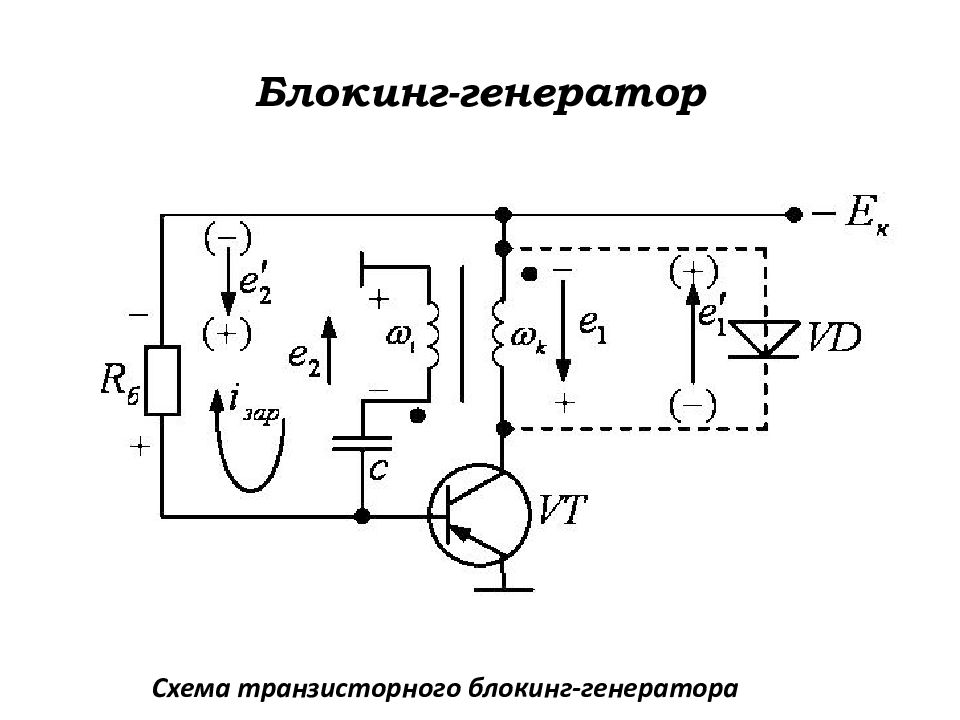
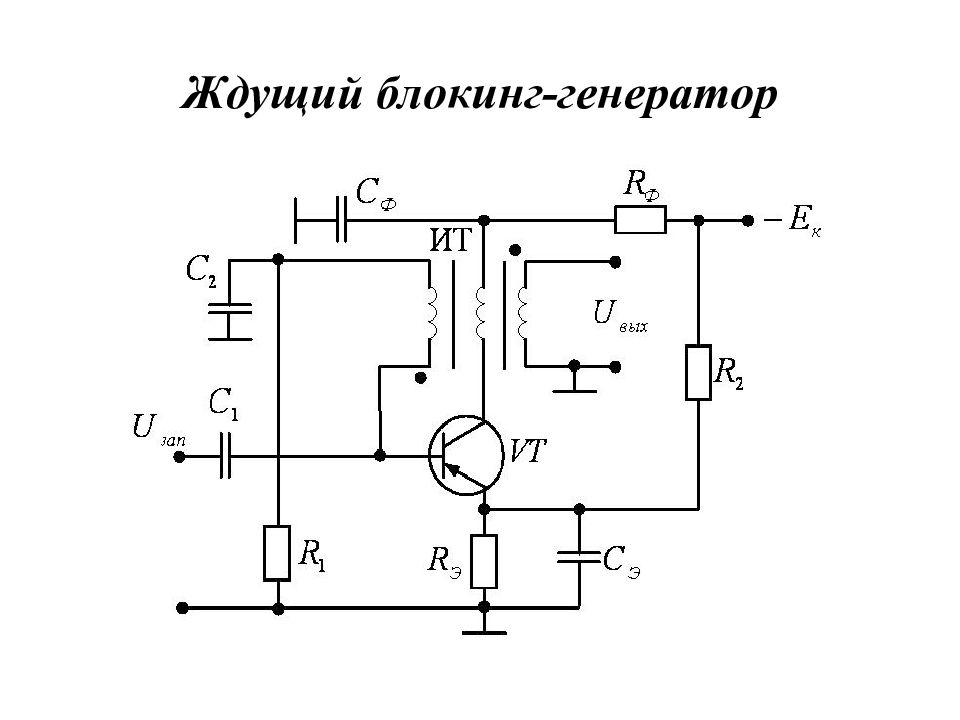
Слайд 160: Блокинг-генератор
Выполнение фазового условия самовозбуждения (т.е. создание положительной обратной связи) обеспечивается соответству-ющим включением обмоток импульсного трансформатора. Блокинг-генератор – это релаксационный генератор коротких импульсов, представляющий собой однокаскадный неинвертирую- щий усилитель с глубокой положительной обратной связью. Импульсный трансформатор – это трансформатор с ферро-магнитным сердечником, служащий для преобразования электри-ческих импульсов длительностью от нескольких наносекунд до десятков микросекунд. Основным требованием, предъявляемым к импульсному трансформатору, является обеспечение минималь-ных искажений генерируемого импульса.
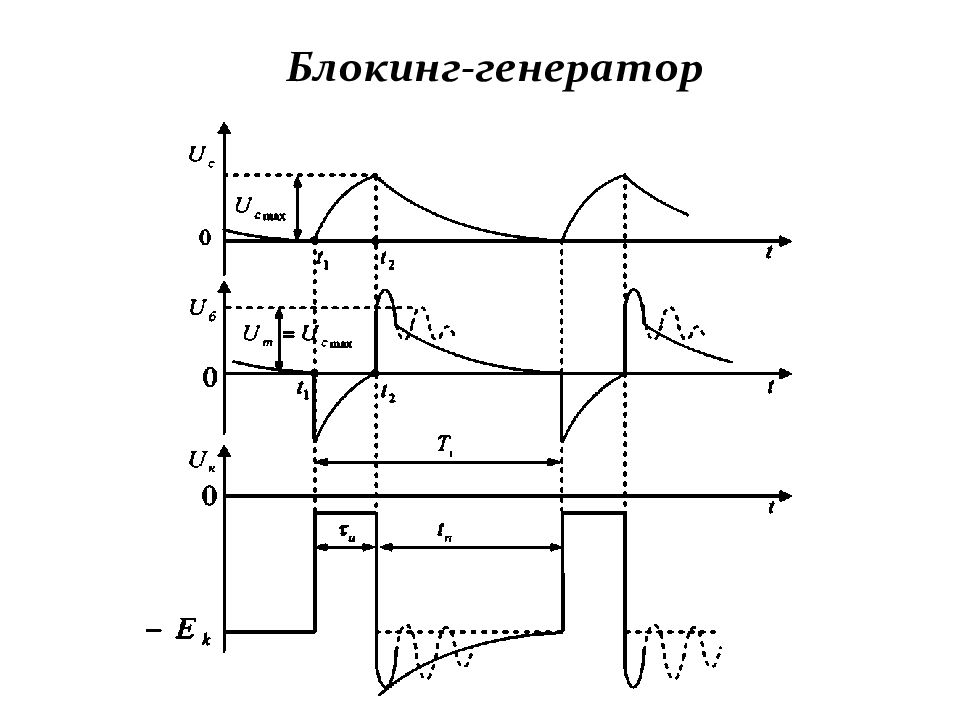
Слайд 163: Работа блокинг-генератора
1-й этап. Перезаряд конденсатора. Конденсатор C, заряженный при формировании предыдущего импульса, перезаряжается по цепи: + Е к (корпус) → ω б → C → R б → – Е к Ток перезаряда создаёт на R б падение напряжения, полярность которого приложена к базе транзистора плюсом. В результате потенциал базы относительно эмиттера оказывается более положительным и поэтому транзистор находится в запертом состоянии. По мере перезаряда конденсатора положительное напряжение на базе уменьшается.
Слайд 164: Работа блокинг-генератора
2-й этап. Первое опрокидывание схемы (прямой блокинг-процесс). + Δ i к → + Δ е 1 → – Δ е 2 → – Δ U б → + Δ i б → + Δ i ' к (> Δ i к )
Слайд 166: Работа блокинг-генератора
3-й этап. Формирование вершины импульса. Начинается заряд конденсатора C током базы по цепи: корпус → переход (Э-Б) → C → ω б → корпус (эмиттер). 4-й этап. Второе опрокидывание схемы (обратный блокинг-процесс). Вновь замыкается петля положительной обратной связи: – Δ i б → – Δ i к → – Δ е' 1 → + Δ е' 2 → Δ U б → – Δ i ' б (> – Δ i б )
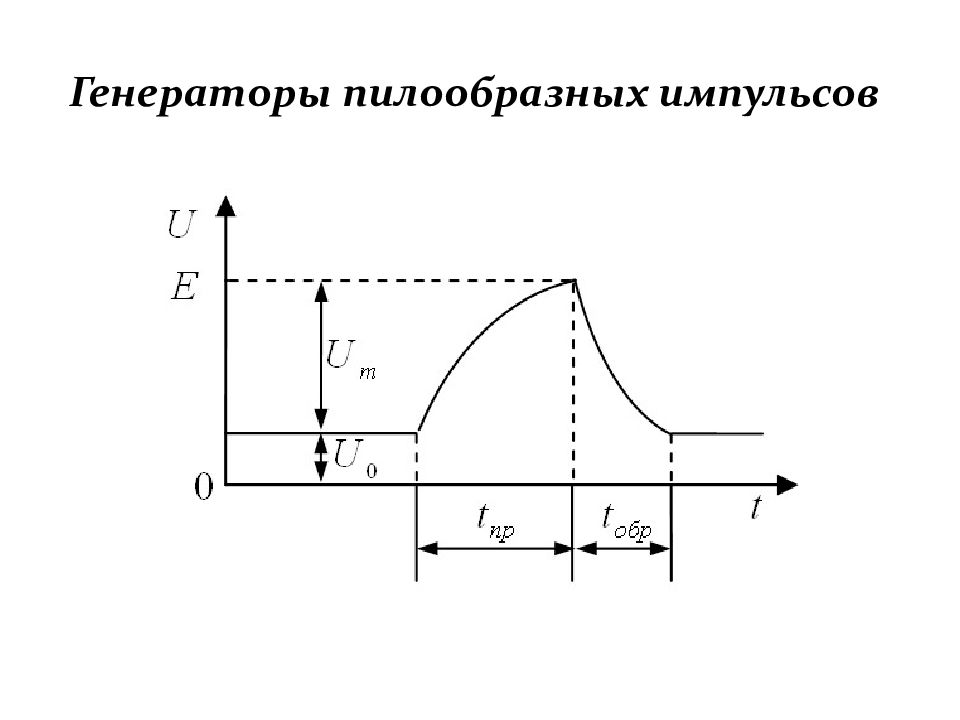
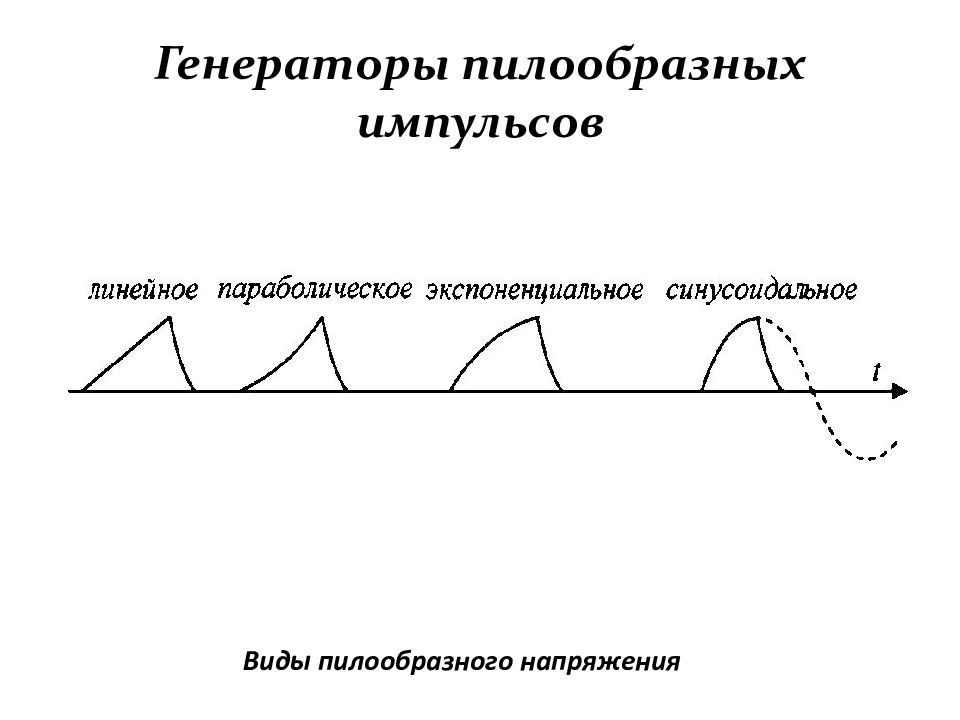
Слайд 168: Генераторы пилообразных импульсов
Импульсами напряжения пилообразной формы называются импульсы, фронт которых изменяется по закону, близкому к линейному. Плоской части у такого импульса нет. В подавляющем большин-стве случаев стремятся получить пилообразное напряжение с максимальной линейностью. Генераторы, вырабатывающие такие импульсы, называются генераторами линейно изменяющегося напряжения (ГЛИН), или генераторами пилообразного напряжения (ГПН).
Слайд 169: Генераторы пилообразных импульсов
Существуют два способа получения ПН: формирование и генери-рование. В первом случае для получения ПН используются формиру-ющие четырёхполюсники (чаще всего, это интегрирующие цепи). Во втором случае ПН получается с помощью генератора, который может работать либо в автоколебательном, либо в ждущем режиме.
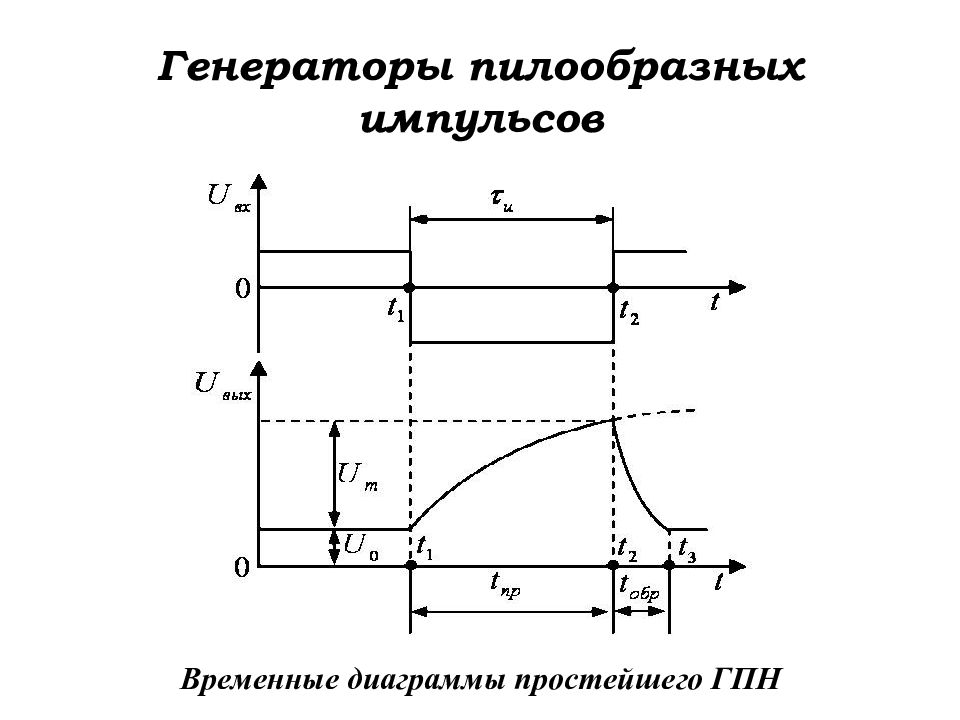
Слайд 172: Параметры пилообразного напряжения
1. Начальный уровень ( U 0 ); 2. Амплитуда ( U m ); 3. Длительность прямого (рабочего) хода ( t пр ); 4. Длительность обратного хода ( t обр ); 5. Средняя скорость нарастания (спадания) переднего фронта ( k ): [ В/с ] 6. Коэффициент нелинейности ( γ ), который показывает, насколько закон изменения напряжения на рабочем участке отличается от идеально линейного; 7. Коэффициент использования напряжения источника питания ( ε ) (%).
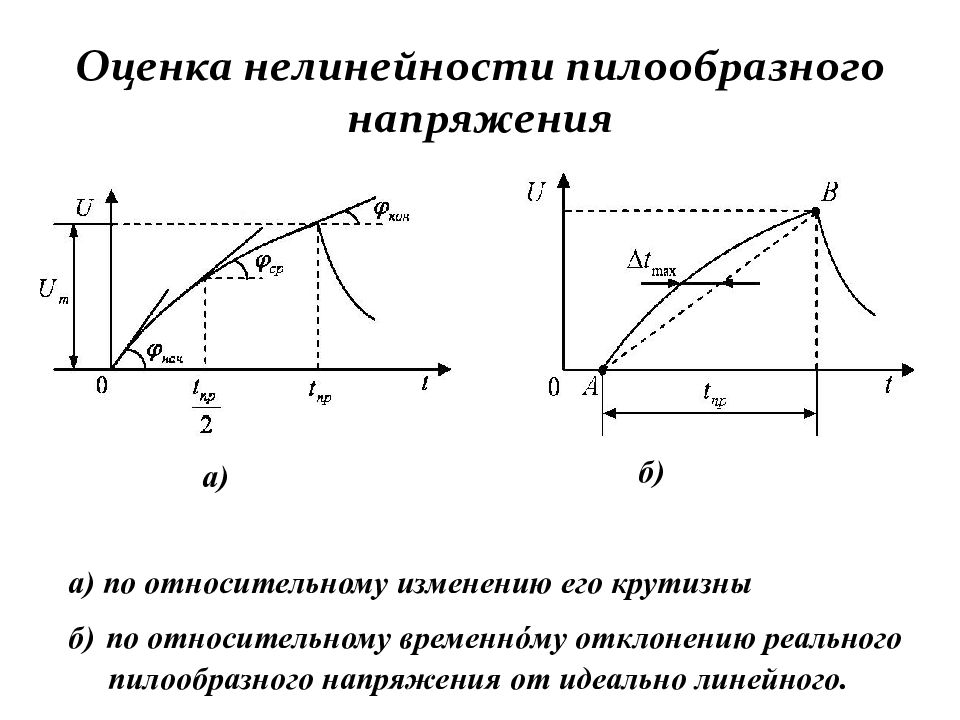
Слайд 173: Оценка нелинейности пилообразного напряжения
а) б) а) по относительному изменению его крутизны б) по относительному временнóму отклонению реального пилообразного напряжения от идеально линейного.
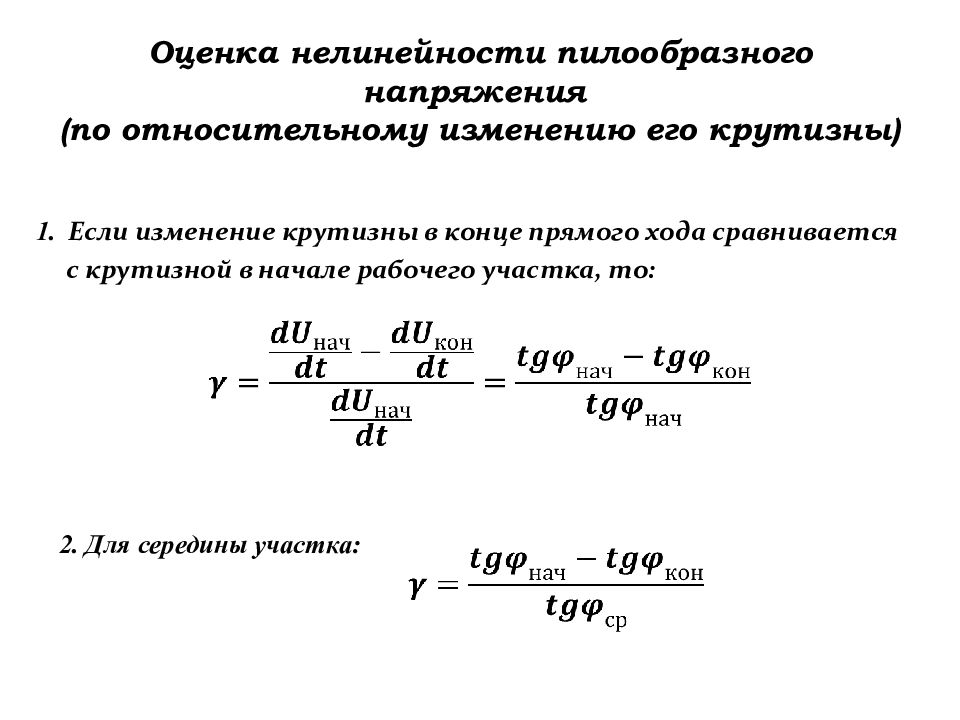
Слайд 174: Оценка нелинейности пилообразного напряжения ( по относительному изменению его крутизны)
2. Для середины участка: 1. Если изменение крутизны в конце прямого хода сравнивается с крутизной в начале рабочего участка, то:
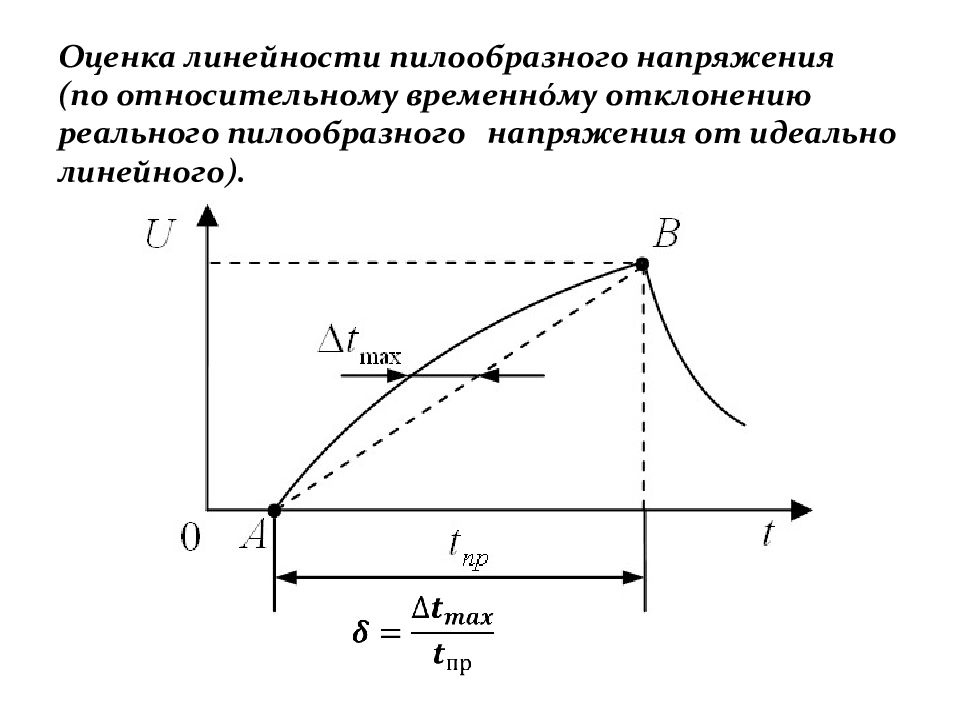
Слайд 175: Оценка линейности пилообразного напряжения (по относительному временнóму отклонению реального пилообразного напряжения от идеально линейного)
Слайд 176: Генераторы пилообразных импульсов
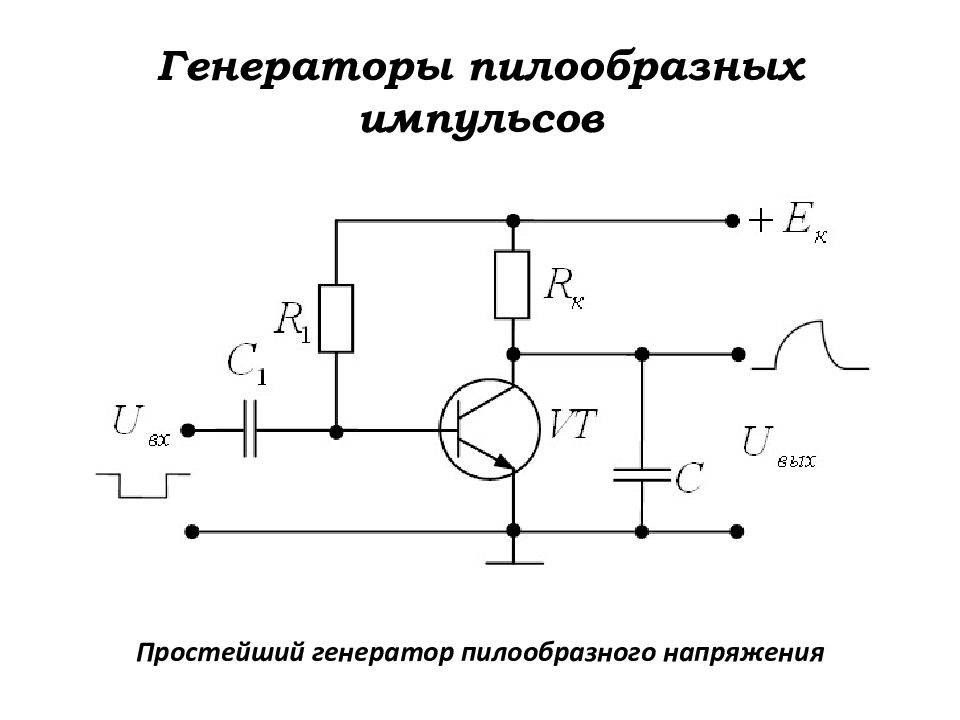
Простейший генератор пилообразного напряжения
Слайд 179: Работа генератора пилообразного напряжения
Напряжение на конденсаторе возрастает по экспоненциальному закону: где Процесс заряда конденсатора происходит в промежутке времени
Слайд 180: Работа генератора пилообразного напряжения
3. Восстановление исходного состояния схемы. Разряд происходит также по экспоненте, но постоянная времени цепи разряда
Слайд 181: Линеаризация пилообразного напряжения
Линеаризация означает достижение максимальной линейности изменения пилообразного напряжения Для повышения линейности используют различные способы, но все они сводятся к реализации одной идеи: для достижения высокой линейности формирующий конденсатор необходимо заряжать (или разряжать) постоянным током.
Слайд 182: Линеаризация пилообразного напряжения
Известно, что Если выполнить условие . , то получим: В этом случае при t = t п р получаем где – коэффициент пропорциональности.
Слайд 183: Принципы линеаризации пилообразного напряжения
Включение в цепь заряда (разряда) формирующего конденсатора токостабилизирующего элемента. 2. Применение обратной связи.
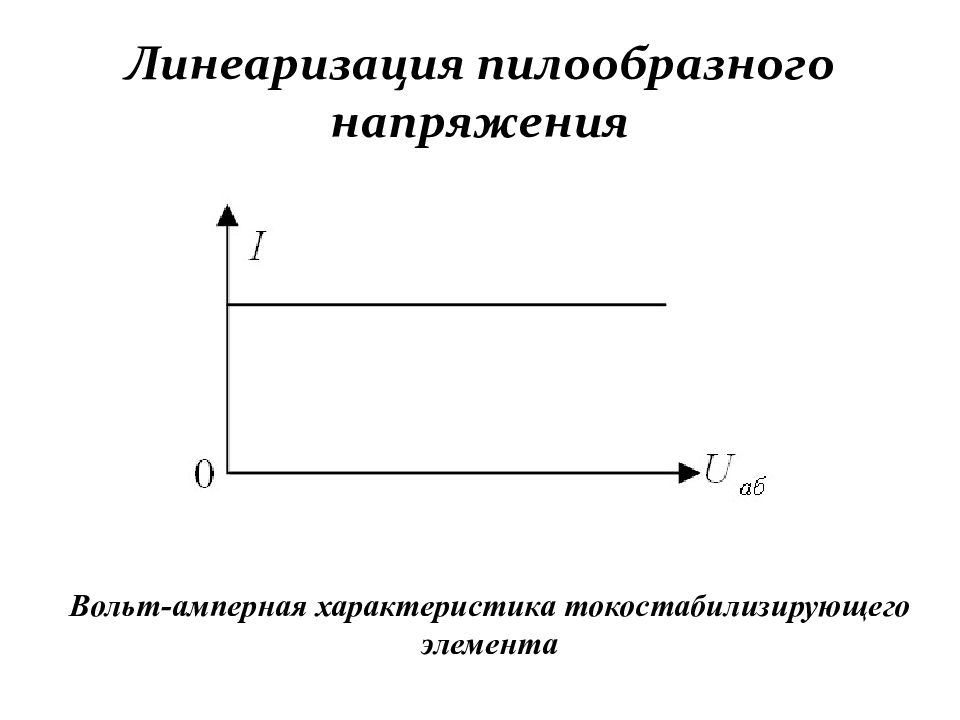
Слайд 184: Линеаризация пилообразного напряжения
Вольт-амперная характеристика токостабилизирующего элемента
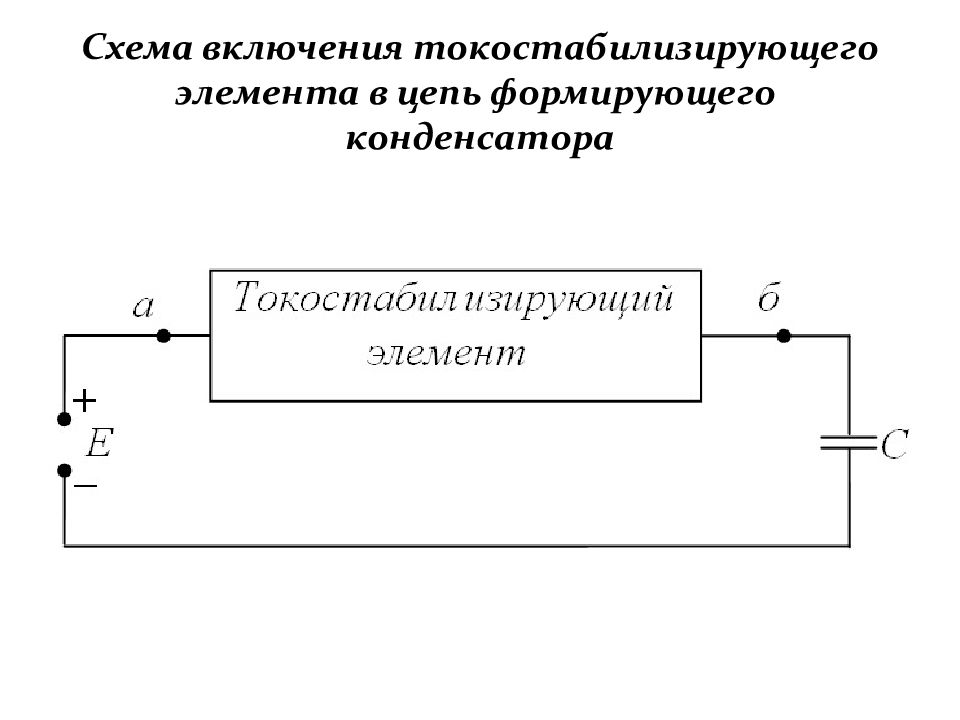
Слайд 185: Схема включения токостабилизирующего элемента в цепь формирующего конденсатора
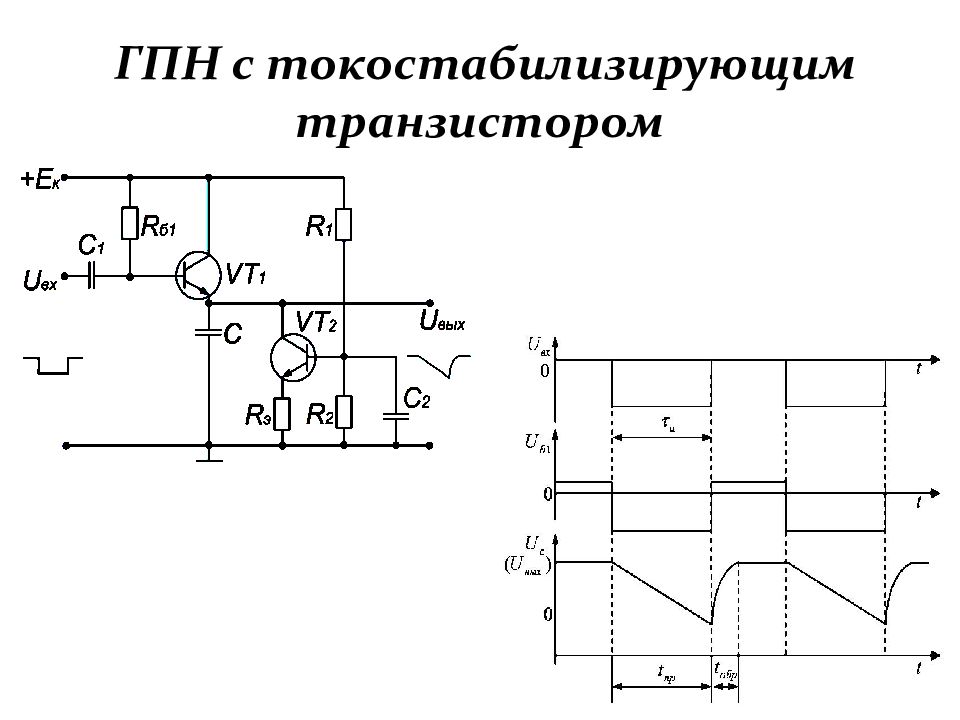
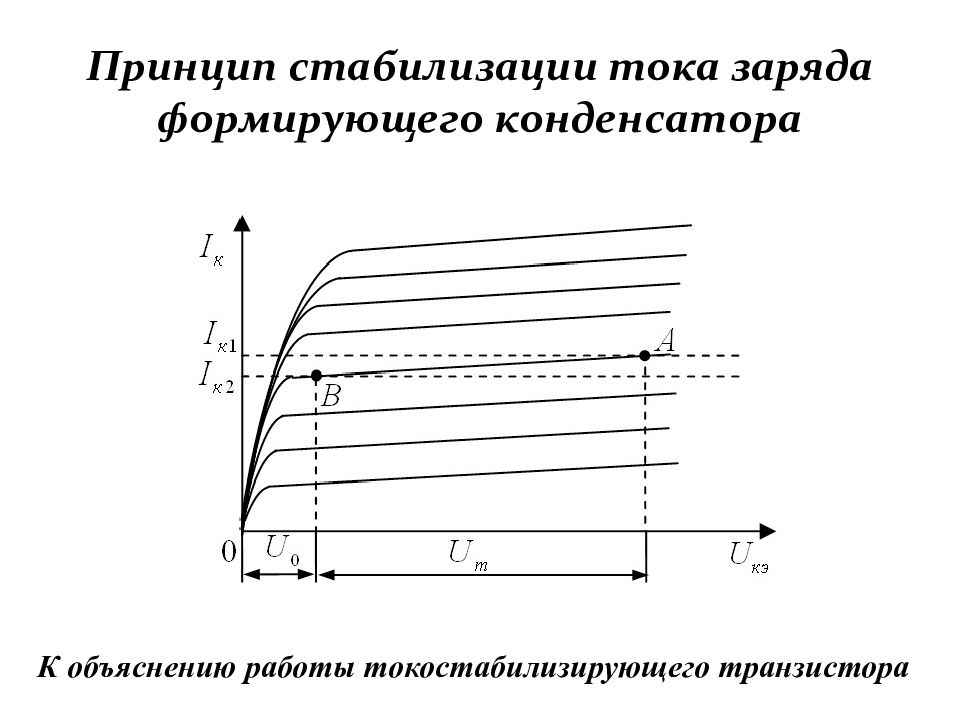
Слайд 187: Принцип стабилизации тока заряда формирующего конденсатора
К объяснению работы токостабилизирующего транзистора
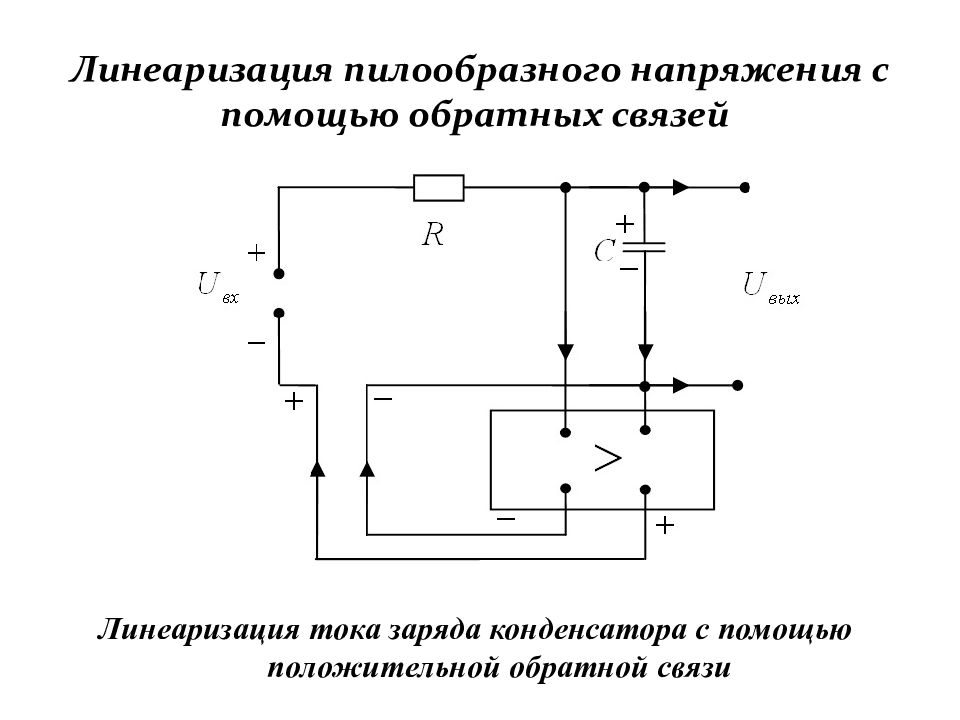
Слайд 188: Линеаризация пилообразного напряжения с помощью обратных связей
Линеаризация тока заряда конденсатора с помощью положительной обратной связи
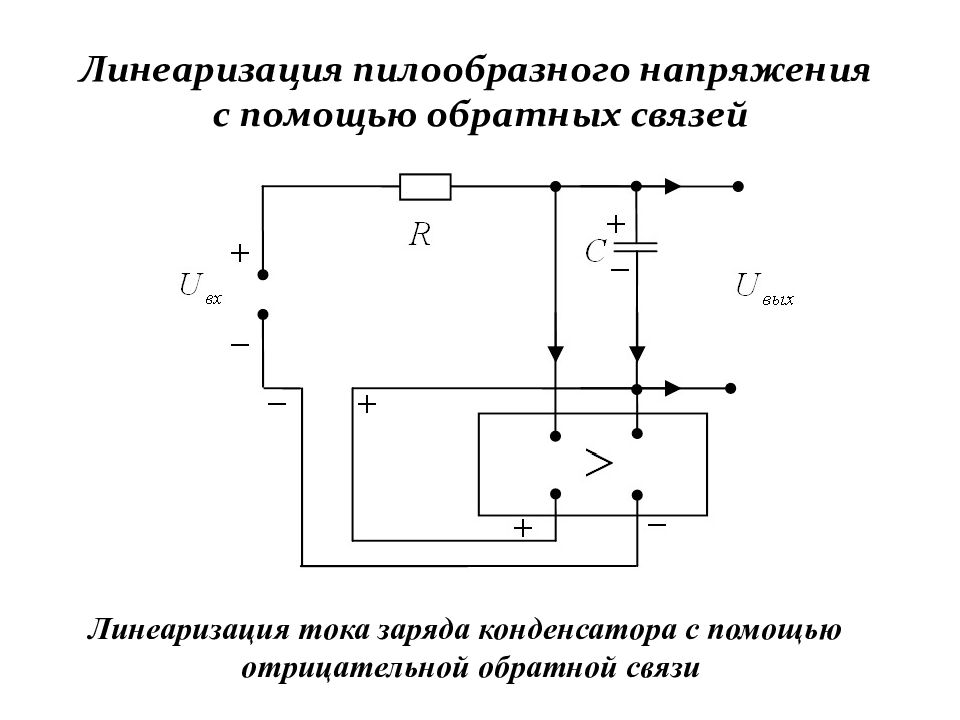
Слайд 189: Линеаризация пилообразного напряжения с помощью обратных связей
Линеаризация тока заряда конденсатора с помощью отрицательной обратной связи
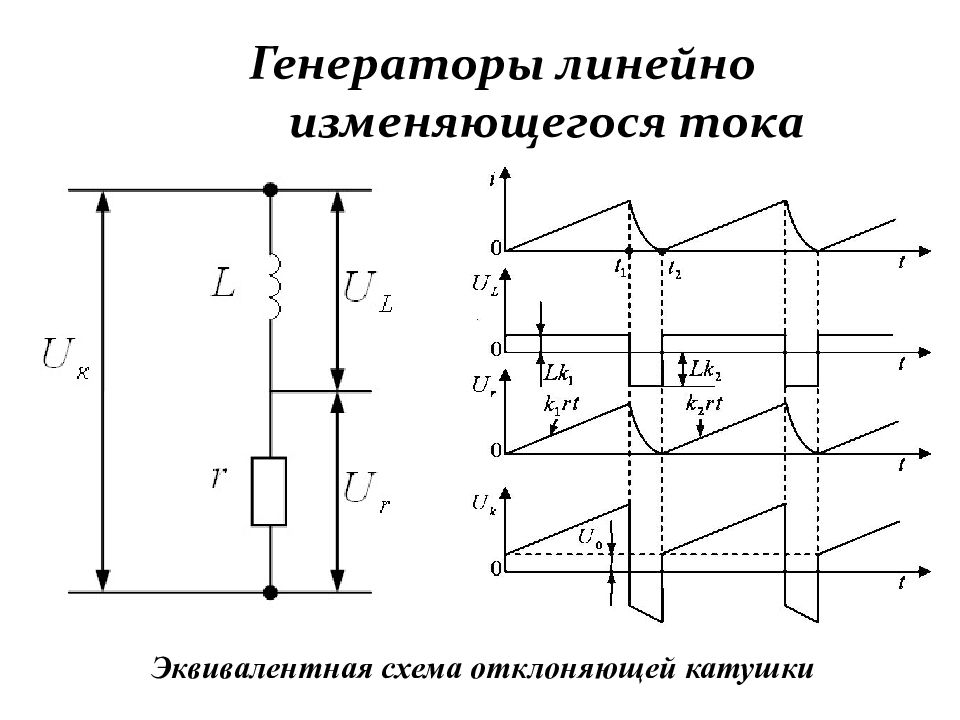
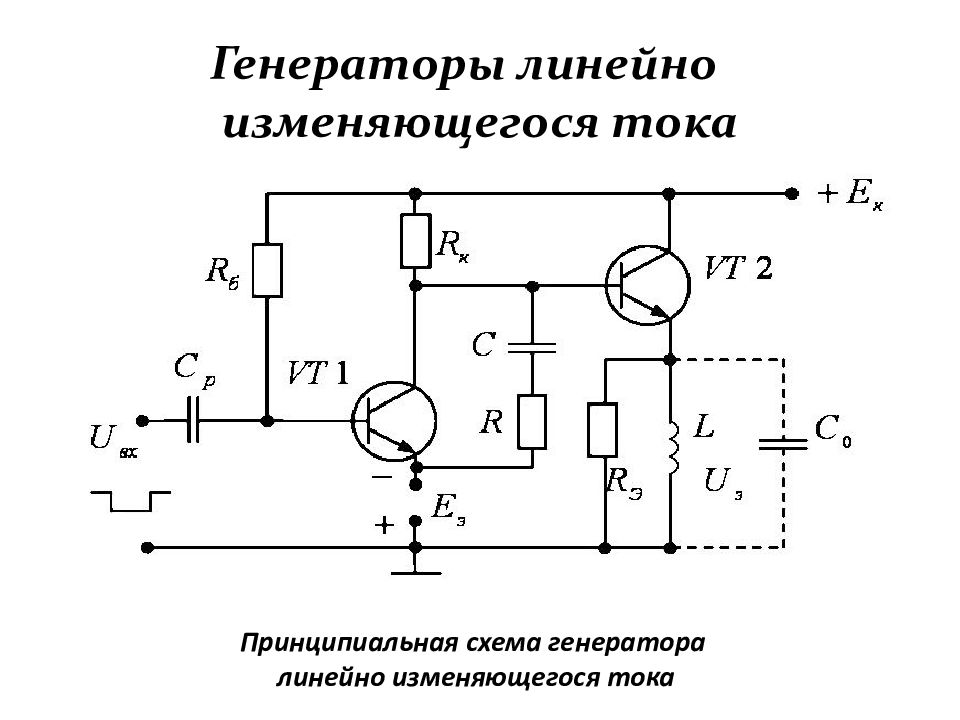
Слайд 191: Генераторы линейно изменяющегося тока
Эквивалентная схема отклоняющей катушки