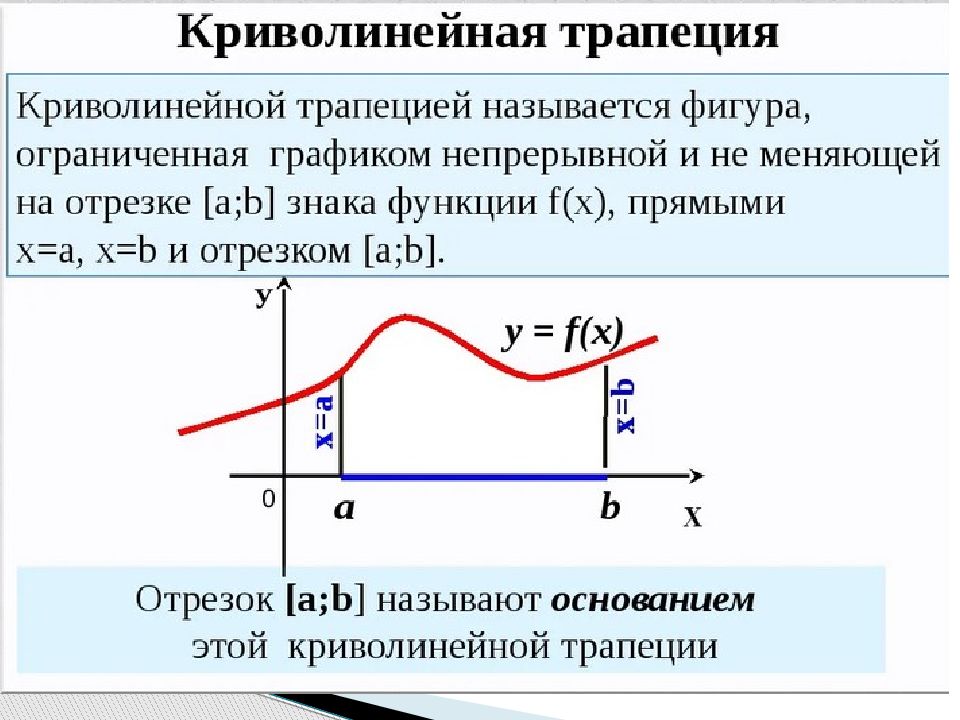
Слайд 2: Цели занятия
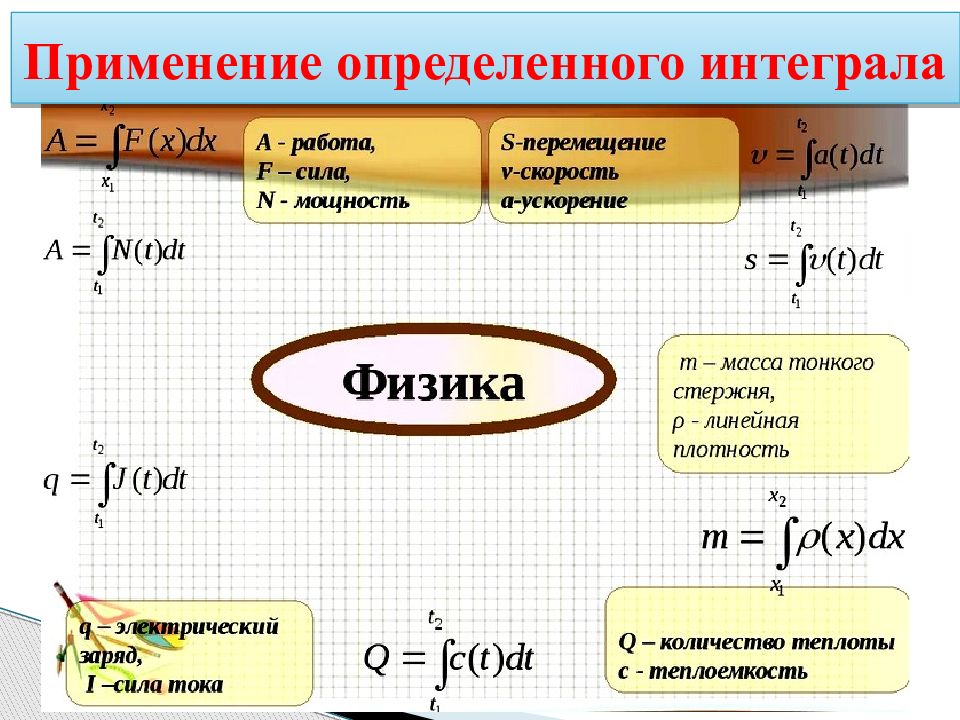
Повторить таблицу первообразных элементарных функций; Ввести понятие определенного интеграла и Формулу Ньютона-Лейбница ; Рассмотреть свойства определенного интеграла; Прорешать примеры; Примененить определенный интеграл для нахождения площади криволинейной трапеции. Рассмотреть применение определенного интеграла в физике. Цели занятия
Слайд 3: Актуализация имеющихся знаний
1.Интегрирование – это… 2. Что называют первообразной функции? 3. Дайте определение определенного интеграла. 4. Найдите определенный интеграл Актуализация имеющихся знаний
Слайд 4
Первообразной для функции f(x) называется такая функция F(x), производная которой равна самой функции f(x) : F'(x) = f(x). О перация нахождения первообразной от заданной функции Определённый интеграл — это тип интеграла, который вычисляется на определённом интервале и результатом которого является конкретное число.
Слайд 8: Свойства определенного интеграла
1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е. Свойства определенного интеграла. 2
Слайд 10
Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если то 5.
Слайд 14
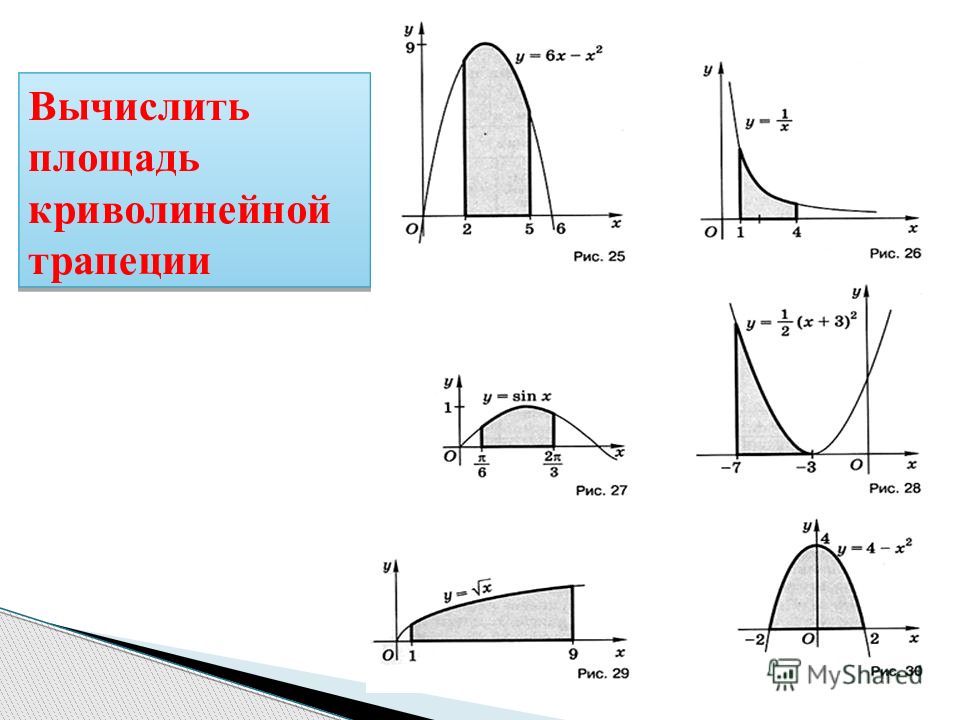
Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, образованной линиями: сверху ограниченной кривой у = f ( x ), и прямыми у = 0; х = а; х = b.
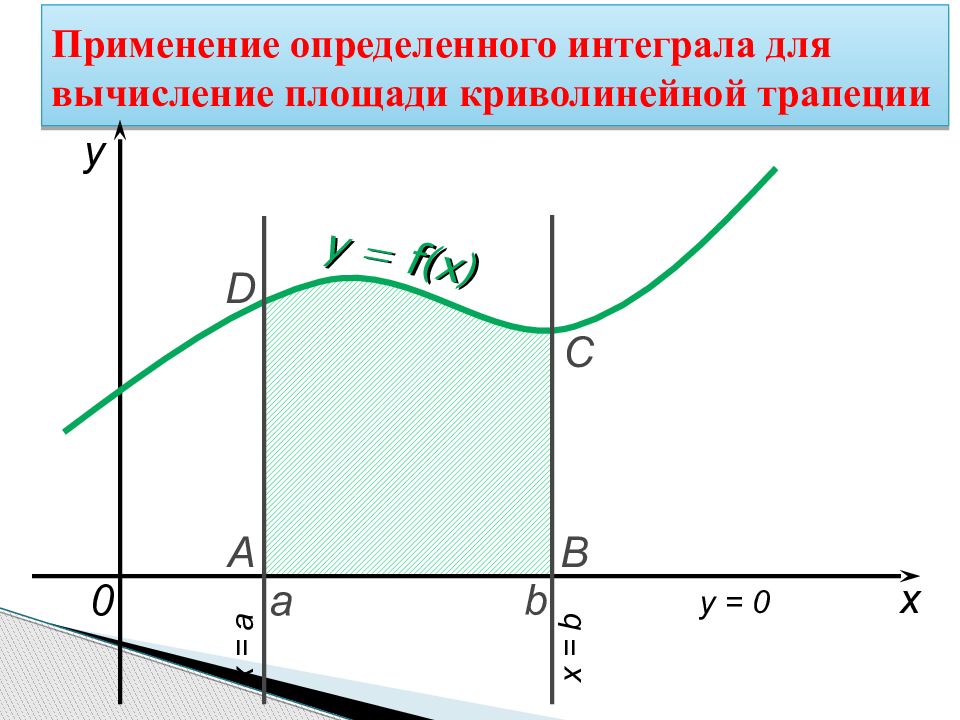
Слайд 15: Применение определенного интеграла для вычисление площади криволинейной трапеции
a b x y y = f(x) 0 A B C D x = a x = b y = 0
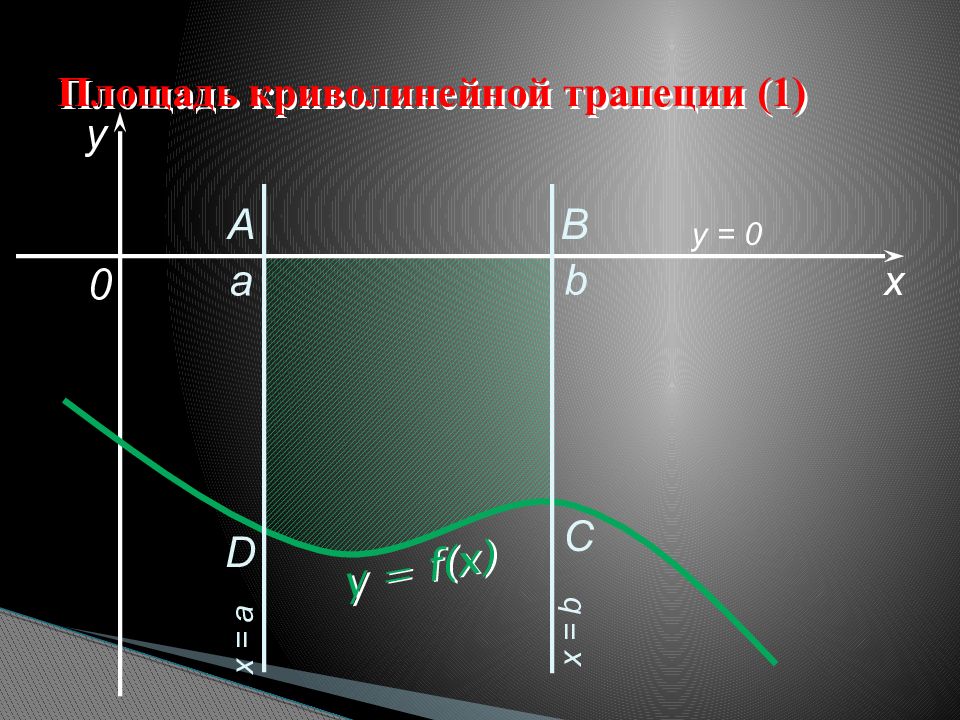
Слайд 16: Площадь криволинейной трапеции (1)
a b x y y = f(x) 0 A B C D x = a x = b y = 0
Слайд 17
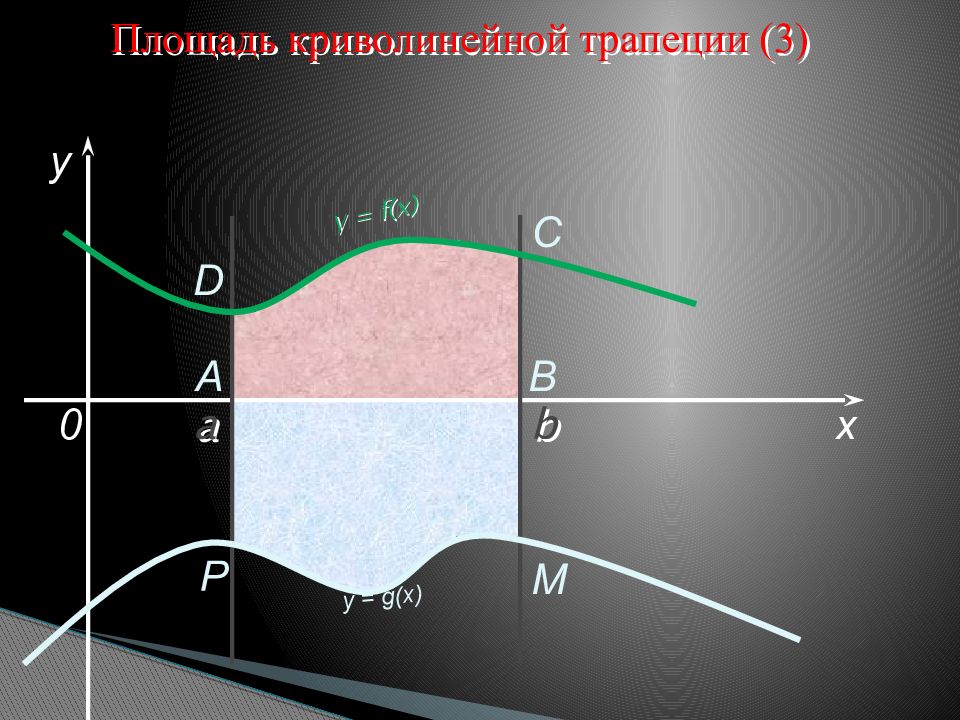
a b x y y = f(x) 0 y = g(x) A B C D M P Площадь криволинейной трапеции (3)
Слайд 22: Подведение итогов. Рефлексия
Что такое определенный интеграл? Кто вывел формулу вычисления определенного интеграла? Где применяется определенный интеграл? Что называют криволинейной трапецией? Что нового ты узнал на занятии…? Какие факты запомнились лучше всего? В чем испытывали затруднения? Как Вы можете оценить свою работу? Подведение итогов. Рефлексия