Функция проводимости нормально замкнутой и нормально разомкнутой реле. Релейно-контактные задачи. Өткізгіштік функциясының қалыпты жабық және қалыпты ашық релесі. Релелік-байланыстың міндеттері.
Релелік байланыс схемасы деп ток көздерінің полюстері кейбір тұтынушымен байланысқан, өткізгіштер мен қос позициялық контактілердің құрылғысы деп атаймыз. Контактілер жабық және ашық болуы мүмкін. Әр контакт кейбір релеге ( коммутаторға ) қосылған. Реле іске қосылған кезде (ток астында ) оған қосылған барлық жабық контактілер жабық, ал ашық контактілер ашық ; немесе керісінше. Әрбір реле өзінің логикалық айнымалысына сәйкес келеді, егер реле іске қосылған болса 1 мәнін қабылдайды, ал керісінше жағдайда 0 мәнін қабылдайды. Сызбаларда x релесіне қосылған барлық жабу контактілері бірдей x символымен, ал ашылатындар символмен көрсетіледі. Релелік байланыс схемалары
Бұл реле х-ке қ осылған кезде оның барлық жабық контактілері х ток өткізеді және ол 1-ге сәйкес келеді, ал барлық ашылған контактілері ток өткізбейді және ол 0-ге сәйкес келеді. Реле ажыратылған кезде карама-карсы жағдай жасалады. Егер тізбек ток өткізсе, 1-ге тең, ал 0-ге тең болса логикалық айнымалы да бүкіл схемага сәйкес келеді. Схемага сәйкес келетін у айнымалысы логикалық функция болып табылады. айнымалылары... тиісті реле. Бұл функция тізбектің өткізгіштік функциясы деп аталады, ал оның кестесі тізбектің жұмыс шарттары деп аталады. Екі релелік байланыс тізбегі эквивалентті деп аталады, егер олардың біреуі ток өткізсе және басқа тізбек ток өткізсе, яғни егер бұл тізбектердің екеуі де бірдей өткізгіштік функцияларга ие болса. Екі эквивалентті схеманың ішінен аз контактілерді қамтитын қарапайым болып саналады. Келесі схемаларды қарастыратын боламыз.
Бұл схема кем дегенде екі тәуелсіз х немесе у қосқыштарының біреуі жабық болған кезде ғана ток өткізеді. Бұл тізбектің өткізгіштік функциясы екі айнымалыдан алынған логикалық функция болады, ол 1 мәнін алады және кем дегенде біреуі 1 мәнін қабылдаған жағдайда ғана логикалық функция бола алады. Бұл дизъюнкция осындай функция болып табылады ;
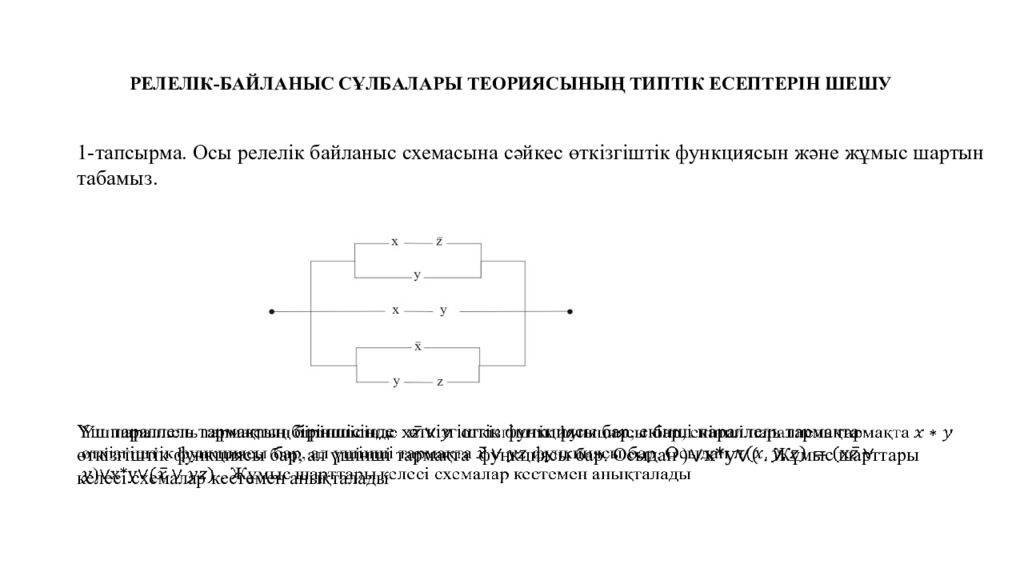
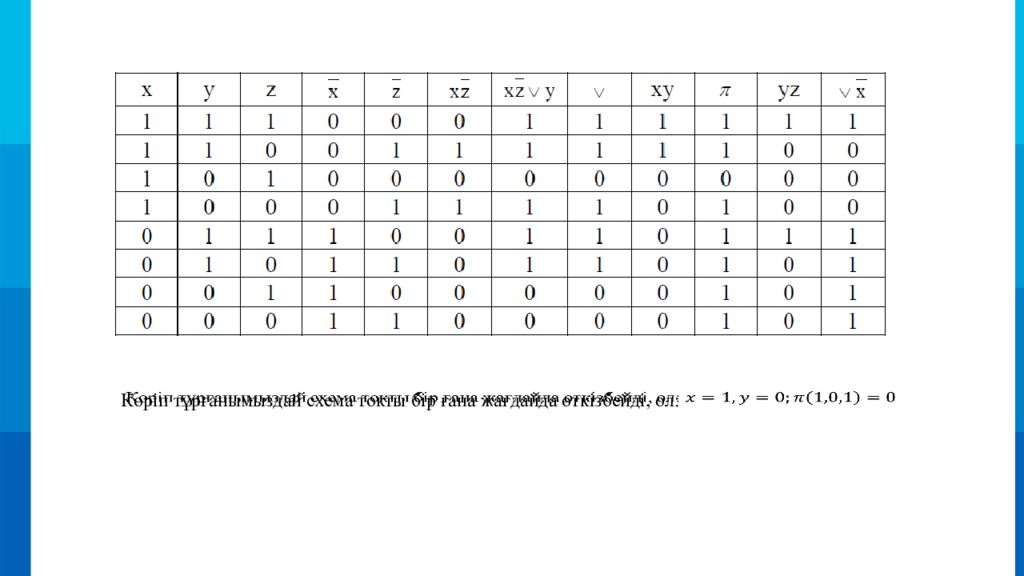
1-тапсырма. Осы релелік байланыс схемасына сәйкес өткізгіштік функциясын және жұмыс шартын табамыз. Үш параллель тармақтың біріншісінде өткізгіштік функциясы бар, екінші параллель тармақта өткізгіштік функциясы бар, ал үшінші тармақта функциясы бар. Осыдан ) ∨x*y∨(. Жұмыс шарттары келесі схемалар кестемен анықталады
Көріп тұрғанымыздай схема токты бір ғана жағдайда өткізбейді, ол :
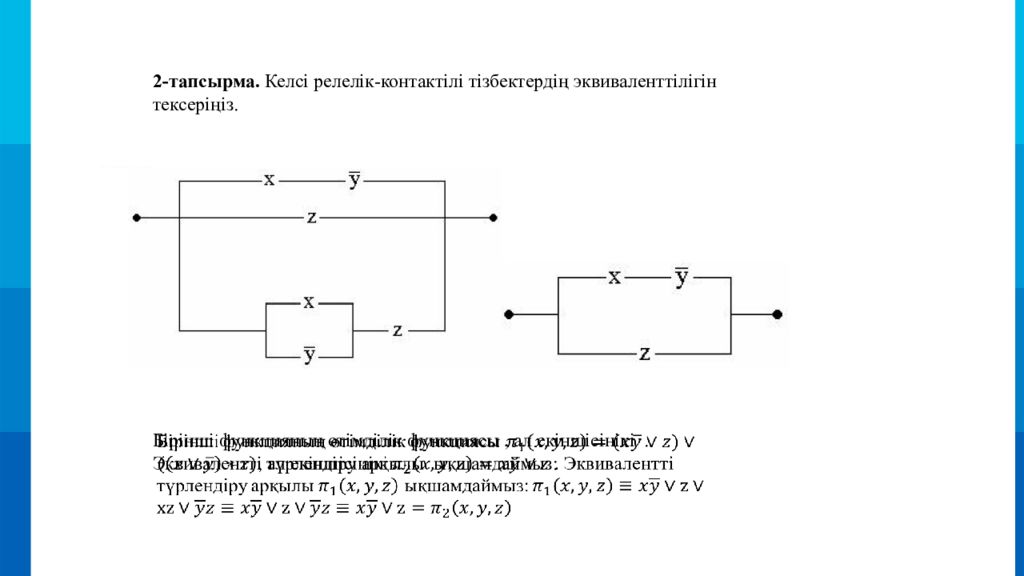
2-тапсырма. Келсі релелік-контактілі тізбектердің эквиваленттілігін тексеріңіз. Бірінші функцияның өтімділік функциясы, ал екіншісінікі. Эквивалентті түрлендіру арқылы ықшамдаймыз :
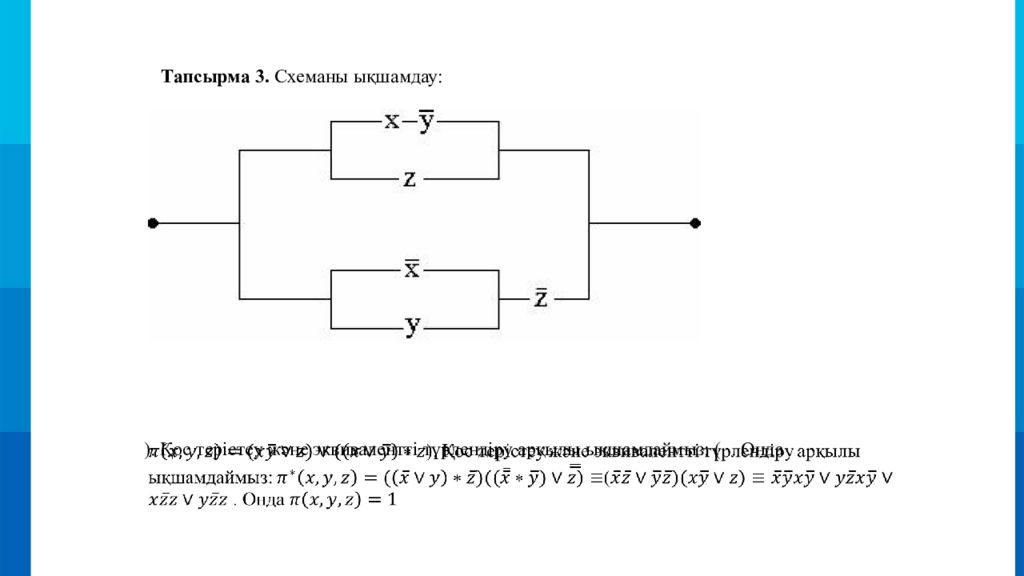
Тапсырма 3. Схеманы ықшамдау : ). Қос терістеу және эквивалентті түрлендіру арқылы ықшамдаймыз : (. Онда
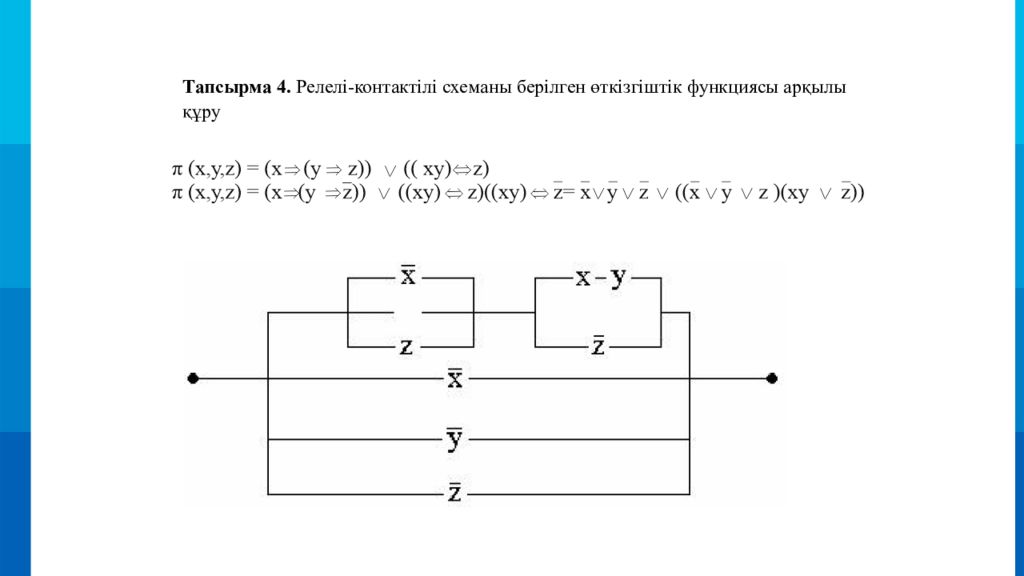
Тапсырма 4. Релелі-контактілі схеманы берілген өткізгіштік функциясы арқылы құру
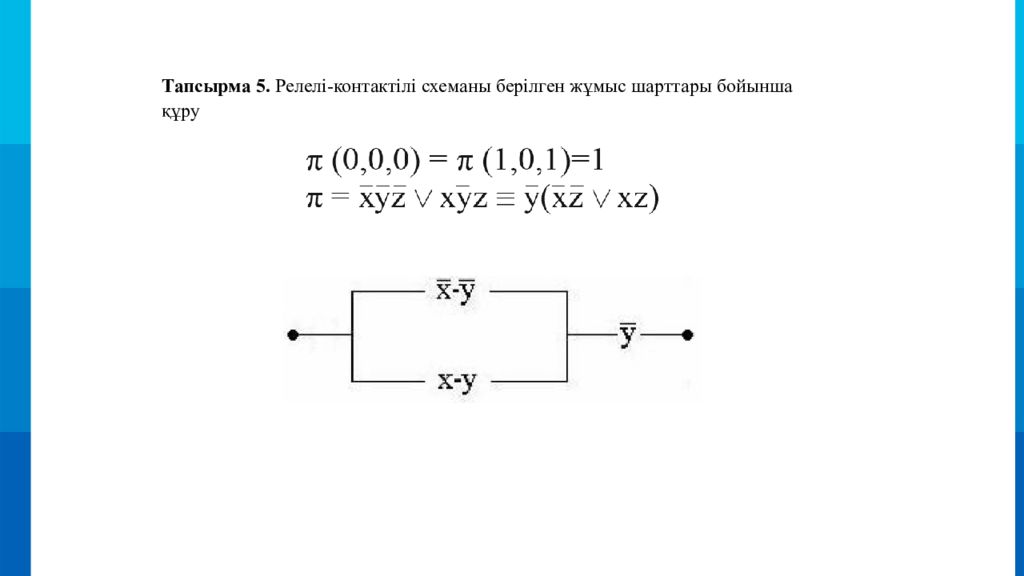
Тапсырма 5. Релелі-контактілі схеманы берілген жұмыс шарттары бойынша құру
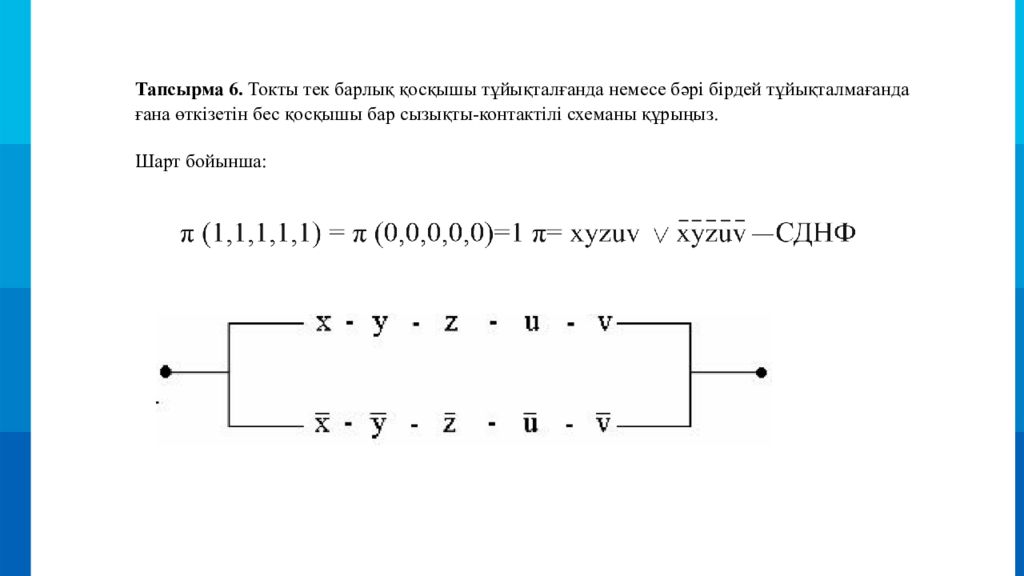
Тапсырма 6. Токты тек барлық қосқышы тұйықталғанда немесе бәрі бірдей тұйықталмағанда ғана өткізетін бес қосқышы бар сызықты-контактілі схеманы құрыңыз. Шарт бойынша :
Бақылау сұрақтары 1.Релелік байланыс схемасы туралы түсінік. 2.Тең релелік байланыс схемалары. 3.Өткізгіштік функциясы қалыпты жабық реле. 4.Өткізгіштік функциясы қалыпты ашық реле. 5.Релелік-байланыс міндеттері.
Әдебиеттер тізімі: 1 Иванов, Б.Н. Дискретная математика. Алгоритмы и программы. Расширенный курс / Б.Н. Иванов. - М.: Известия, 2011. - 512 c. 2 Иванов, О.А. Дискретная математика. Учебник для вузов / О.А. Иванов, Г.М. Фридман. - СПб.: Питер, 2014. - 296 c. 3 Соболева, Т.С. Дискретная математика: Учебник / Т.С. Соболева. - М.: Академия, 2018. - 240 c. 4 Ерусалимский, Я.М. Дискретная математика. Теория и практикум: Учебник / Я.М. Ерусалимский. - СПб.: Лань, 2018. - 476 c. 5 Астраханцева Л.Н., Байсалова М.Ж. Дискретная математика. Конспект лекций для студентов всех форм обучения специальности 5В070300-Информацион. системы. - Алматы: АУЭС, 2014. - 35 с. 6 Астраханцева Л.Н. Дискретная математика. Учебное пособие. - Алматы: АУЭС, 2011. - 98 с. Интернет көздері: 7 http://mathhelpplanet.com/static.php?p=primeneniye-bulevykh-funktsiy-k-skhemam 8 https://slide-share.ru/primenenie-bulevikh-funkcij-k-relejno-kontaktnim-skhemam-155818
Назарларыңызға рахмет!
