Слайд 2: KAYNAKLAR
AKSOY, A.: “JEODEZİ I, II Ders Notu”, İTÜ, İnşaat Fakültesi, Jeodezi ve Fotogrametri Müh. Bölümü, Jeodezi Kürsüsü Yayınları, No:3, 1980. ULUSOY, E.: “Matematiksel Jeodezi”, İ. D. M. M. Akademisi Yayınları, Sayı:144, Kurtuluş Matbaası, İstanbul, 1977. RAPP, R. H.:“ Geometric Geodesy I, II”, The Ohio State University, Department of Geodetic Science, Columbus, 1975. DRAGOMİR, V. C. Et al.: “ Theory of the Earth’s Shape ”, Elseiver Scientific Publishing Company, Amsterdam, 1982. BOMFORD, G.:“ Geodesy ”, Clarendon Press, Oxford, 1980. HOTİNE, M.:“Mathematical Geodesy ”, ESSA Mongr. 2, Washington, 1969. TORGE, W.:“ Geodesy ”, New York, 1980.
Слайд 3: История геодезии
В течение всей истории человечества страсть к пониманию облика и размеров Земли, параллельно с процессом развития цивилизаций, сыграла важную роль в развитии геодезии. История геодезии считается начавшейся с древнегреческой цивилизации. В 9 веке до н. э. Гомер в своей "Илиаде" описывает Землю как плоский диск, окруженный океанами. Анаксимандр (610-546 гг. до н. э.) утверждал, что Земля имеет форму цилиндра, ориентированного с востока на запад. Анаксимен (585-525 гг. до н. э.) считал, что Земля подвешена в вакууме, как плоская плита.
Слайд 4: История геодезии
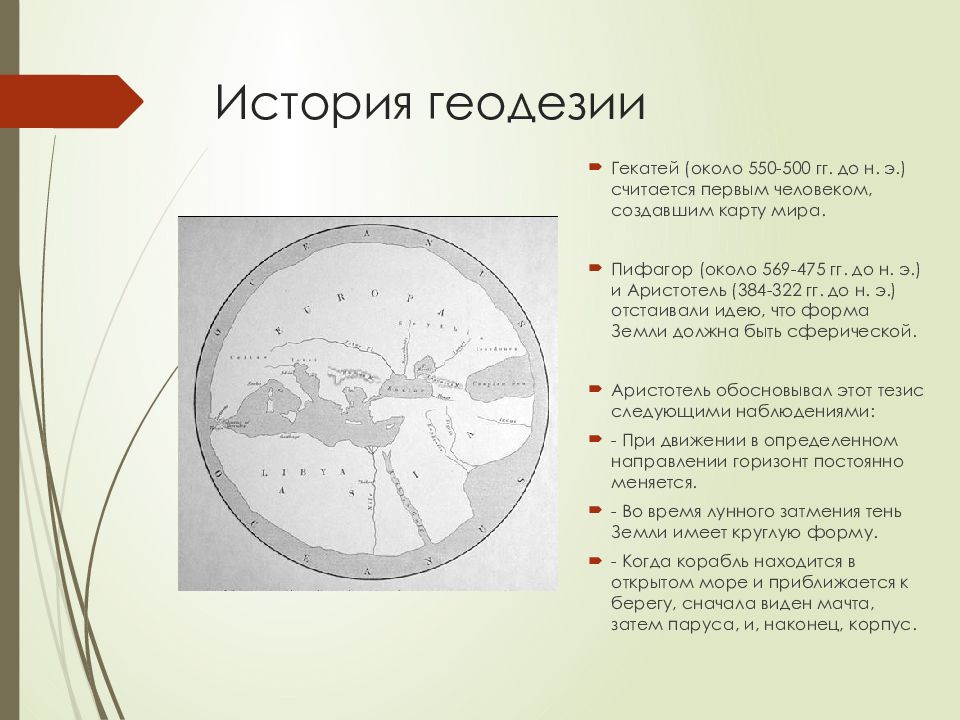
Гекатей (около 550-500 гг. до н. э.) считается первым человеком, создавшим карту мира. Пифагор (около 569-475 гг. до н. э.) и Аристотель (384-322 гг. до н. э.) отстаивали идею, что форма Земли должна быть сферической. Аристотель обосновывал этот тезис следующими наблюдениями: - При движении в определенном направлении горизонт постоянно меняется. - Во время лунного затмения тень Земли имеет круглую форму. - Когда корабль находится в открытом море и приближается к берегу, сначала виден мачта, затем паруса, и, наконец, корпус.
Слайд 5: Jeodezinin Tarihi, Tanımı, Amacı ve Referans Modelleri
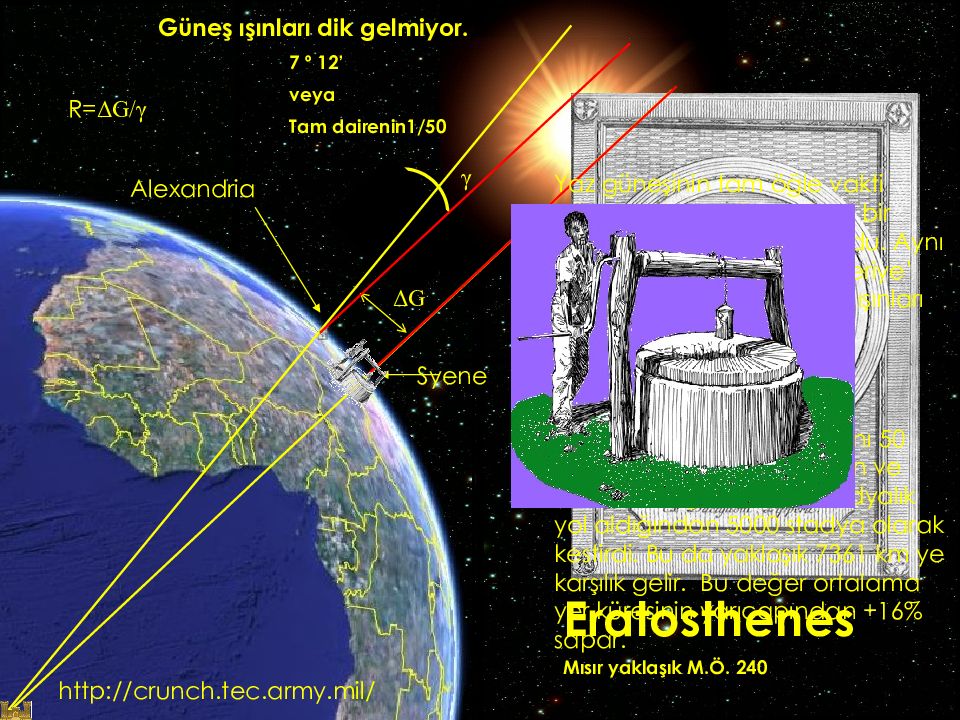
Eratosthenes Mısır yaklaşık M.Ö. 240 Syene Alexandria 7 º 12’ veya Tam dairenin 1/50 Güneş ışınları dik gelmiyor. Yaz güneşinin tam öğle vakti güneş ışınlarının Syene ’ de bir kuyuya dik düştüğünü buldu. Aynı meridyen üzerinde İskenderiye’ de, aynı zamanda güneş ışınları düşey doğrultu ile bir açı oluşturuyordu (7° 12'). Syene ile İskenderiye arasını 50 günlük deve yürüyüşünden ve develer bir günde 100 stadyalık yol aldığından 5000 stadya olarak kestirdi. Bu da yaklaşık 7361 km ye karşılık gelir. Bu değer ortalama yer küresinin yarıçapından +16% sapar. R= Δ G/ γ Δ G γ http://crunch.tec.army.mil/
Слайд 6: История геодезии
Посидоний (около 135-51 гг. до н. э.) измерил меридианное расстояние между Александрией и Родосом и вычислил радиус Земли с погрешностью +11%. Это был важный шаг в изучении формы Земли на ранних этапах развития геодезии. В средние века в Европе вопрос о форме Земли не исследовался активно. С другой стороны, в исламской цивилизации во времена халифа Аль-Мамуна, Эль-Хорезми в Багдаде, примерно в 827 году н. э., измерил дугу меридиана и вычислил радиус Земли с погрешностью +10%. Это также было важным вкладом в понимание формы Земли в то время.
Слайд 7: История геодезии
В период Ренессанса научные достижения также оказали влияние на геодезию. Вот несколько примеров этих достижений: - В 1611 году Иоганн Кеплер изобрел телескоп, который также оказал влияние на развитие геодезии. - В 1589 году датский ученый Тихо Браге и голландский ученый Вильгельм Снеллиус разработали принципы триангуляции, которые также стали важными для геодезии. - Вильгельм Снеллиус (1591–1626) смог измерить длину дуги меридиана в Голландии с использованием метода триангуляции. Эта работа стала отправной точкой для использования геодезических измерительных инструментов и сетей триангуляции при измерении длин меридианных дуг. - В 1666 году Парижская академия наук взяла на себя инициативу в области геодезии, и Франция стала лидером в этой области в 17-18 веках. - Французский ученый Жан Пикар в 1669/70 годах совершил измерение дуги меридиана между Малвуазеном и Амьеном в рамках триангуляции. Полученное им значение радиуса Земли имело погрешность +0.1%.
Слайд 8: История геодезии
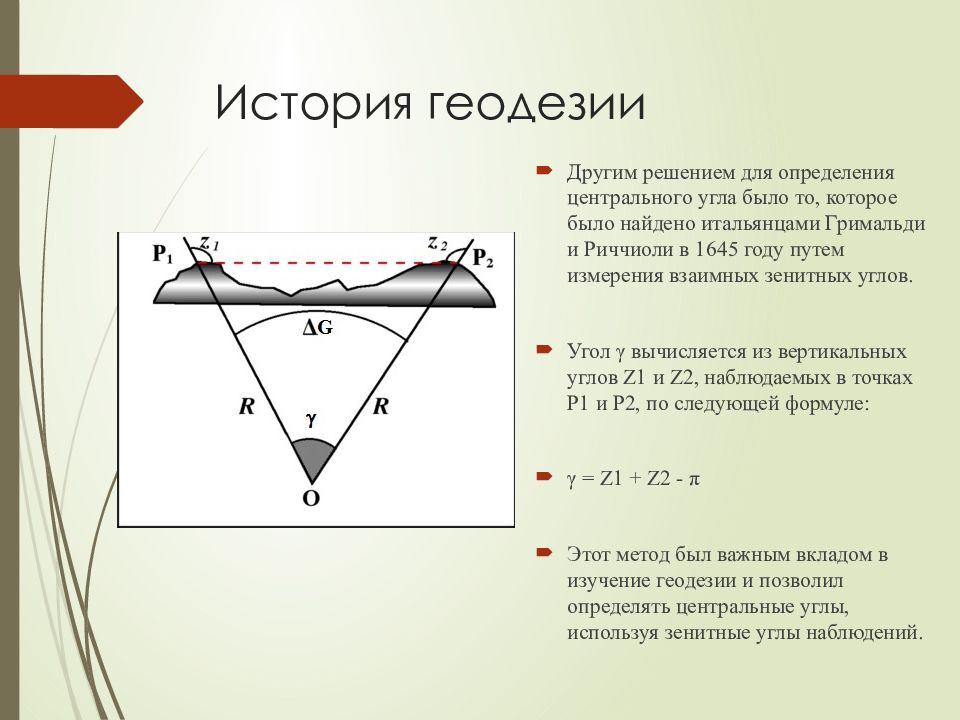
Другим решением для определения центрального угла было то, которое было найдено итальянцами Гримальди и Риччиоли в 1645 году путем измерения взаимных зенитных углов. Угол γ вычисляется из вертикальных углов Z1 и Z2, наблюдаемых в точках P1 и P2, по следующей формуле: γ = Z1 + Z2 - π Этот метод был важным вкладом в изучение геодезии и позволил определять центральные углы, используя зенитные углы наблюдений.
Слайд 9: История геодезии
6. и 17. веках начали появляться новые наблюдения и идеи из астрономии и физики относительно местоположения и формы Земли в космосе. - Коперник (1473-1543) переход от геоцентрической модели мира Птолемея к гелиоцентрической системе, где Солнце находится в центре, считается важным событием. - Кеплер (1571-1630) открыл законы движения планет, которые стали известны как законы Кеплера. - Галилео Галилей (1564-1642) внес вклад в развитие современной механики, изучая такие явления, как свободное падение и законы маятника.
Слайд 10: История геодезии
В 1666 году астроном Кассини наблюдал, что Юпитер имеет сжатые полюса. Астроном Ришер в 1672 году заметил, что его маятниковые часы отставали из-за воздействия гравитации. Исходя из теорий Ньютона (1634-1727) и Гюйгенса (1629-1695), было предположено, что из-за вращения Земли вокруг своей оси возникающая центробежная сила должна уменьшать сжатие к полюсам, что должно приводить к созданию уплощенного эллипсоида у Земли. Для геометрической проверки модели эллипсоида требовались измерения дуг на разных широтах. Длина дуги (меридиана с разницей в 1 градус широты) увеличивается по мере движения с экватора к полюсам из-за уплощения полюсов. Ранее проведенные измерения дуг (Снеллиус, Пикар и др.) указывали на выпуклость модели Земли вместо уплощения у полюсов. С учетом теорий физиков, Парижская академия наук приняла решение провести новую кампанию измерений, в ходе которой уточнить длину дуги в направлении севера и юга. Новые измерения, проведенные под руководством семьи Кассини, показали, что длина дуги в 1 градусе уменьшается по мере движения к полюсам. Это привело к еще большему разгоранию спора между геодезистами и физиками, так как означало, что уплощение земного эллипсоида находится не в полюсах, а, наоборот, в экваториальной области. Для разрешения спора Парижская академия наук решила провести новую кампанию измерений в районах экватора и полюсов.
Слайд 11: История геодезии
Первая экспедиция в Перу (1734-1741) под руководством Годена, Ла Кондамина и Буже была отправлена в район примерно -1.5 градуса широты. В то же время вторая экспедиция в Лапландию (около 66.3 градуса широты) была организована под руководством Мопертиуса и Клеро. Обе экспедиции использовали метод триангуляции для измерения длины дуги, соответствующей разнице в 1 градусе широты. Когда стало ясно, что дуга в Лапландии оказалась длиннее, чем в Перу, было установлено, что модель Земли представляет собой уплощенный эллипсоид в полюсных областях. Клеро (1713-1765), анализируя эти измерения в сочетании с измерениями гравитации, смог доказать физическую и геометрическую совместимость эллипсоидной модели Земли.
Слайд 12: История геодезии
Günümüze gelindiğinde modern ölçme teknikleri sayesinde yer yuvarı hakkındaki tüm bilgiler elde edilebilmektedir. Özellikler yapay uydulara dayalı ölçme teknikleri, modellemelerde kullanılan plaka tektonik modelleri, SLR ( Satellite Laser Range ) ölçümleri, VLBI ( Very Long Baseline İnterferometre) ölçümleri yeryuvarının modellenmesinde etkin bir şekilde kullanılmaktadır. Uluslar arası kuruluşlar IAG ( International Association of Geodesy ) IUGG ( International Union of Geodesy and Geophysics ) IAU ( International Astronomical Union ) BIH ( Bureau International de L’Heure ) IERS ( International Earth Rotation Service) BGI ( Bureau Gravimetrique International IGS ( International GPS Service for Geodynamics ) IGeS ( International Geoid Service) bu çalışmalarda büyük rol almaktadır.
Слайд 13: Jeodezinin Tanımı ve Amacı
Jeodezi ( jeo =yer ve dezi =ölçmek, bölmek) yer yuvarını bölmek, ölçmek anlamına gelmektedir. Helmert (1880)’ e göre “ Yeryüzünün açınımı (projeksiyonu) ve tamamının ölçülmesi bilimi ” olarak tanımlanır. Bu tanım yer yuvarının gravite alanının belirlenmesini içerir. Yeryüzü gerçekte şeklini yeryuvarının gravite alanından alır ve jeodezide çoğu gözlem söz konusu alanın etkisi altındadır.
Слайд 14: Jeodezinin Tanımı ve Amacı
Günümüzdeki teknolojik gelişmelere paralel olarak “ Jeodezi,yeryuvarının ve diğer gök cisimlerinin dış gravite alanı ile biçimini ve ortalama yer elipsoidini zamanın fonksiyonu olarak yer yüzünde ve dışında yapılmış gözlemlerden belirlemektir.”
Слайд 15: Jeodezinin Tanımı ve Amacı
Jeodezi; yeryuvarı ölçmeleri, ülke ölçmeleri, ayrıntı ölçmeleri alanlarına ayrılabilir. Yer yuvarı ölçmeleri: Yeryuvarının geometrik şeklinin belirlenmesi Yeryuvarının gravite alanının ve jeoidin belirlenmesi Yeryuvarının şekli ve gravite alanındaki, zamana bağlı değişimlerin izlenmesi şeklinde tanımlanabilir.
Слайд 16: Jeodezinin Tanımı ve Amacı
Ülke ölçmeleri; ülkenin yüzeyini yeterli sayıda sabit noktaların (nirengi noktaları) koordinatları yardımıyla elde etmektir. Bu temel çalışmalarda yeryuvarının büyük alansal eğrilik ilişkileri dikkate alınmalıdır. Ayrıntı ölçmeleri; topoğrafik ölçmeler, Kadastro ölçmeleri yardımıyla yeryüzünün ayrıntısal biçimi elde edilir. Bu durumda referans yüzeyi olarak yatay düzlem yeterli olacaktır.
Слайд 17: Jeodezinin Tanımı ve Amacı
Yeryuvarı, Ülke ve Ayrıntı ölçmeleri arasında karşılıklı etkileşimler vardır. Ülke ölçmeleri yeryuvarı ölçmelerince saptanmış olan parametreleri kullanır ve kendi sonuçlarını yeryuvarı ölçmelerine sunar. Ayrıntı ölçmeleri, ülke ölçmelerinin sabit nokta ağına geniş ölçüde bağlanır ve ülke haritalarının geliştirilmesine yardımcı olur.
Слайд 18: Jeodezinin Tanımı ve Amacı
Günümüzde yapılan bilimsel çalışmalarda jeodezi alanında üzerinde durulan konular: Plaka tektoniğinin belirlenmesi, Gravite değişimlerinin incelenmesi, GPS yardımıyla sürekli gözlem yapan ağların kurulması, 3 boyutlu konumlama yapabilmek için referans sistemlerinin belirlenmesi, Bu belirlenen referans sistemlerinin uygulamaya geçirilerek referans çatılarının oluşturulması (ITRS ITRF) şeklinde örnek verilebilir.
Слайд 19: Referans Yüzeyleri
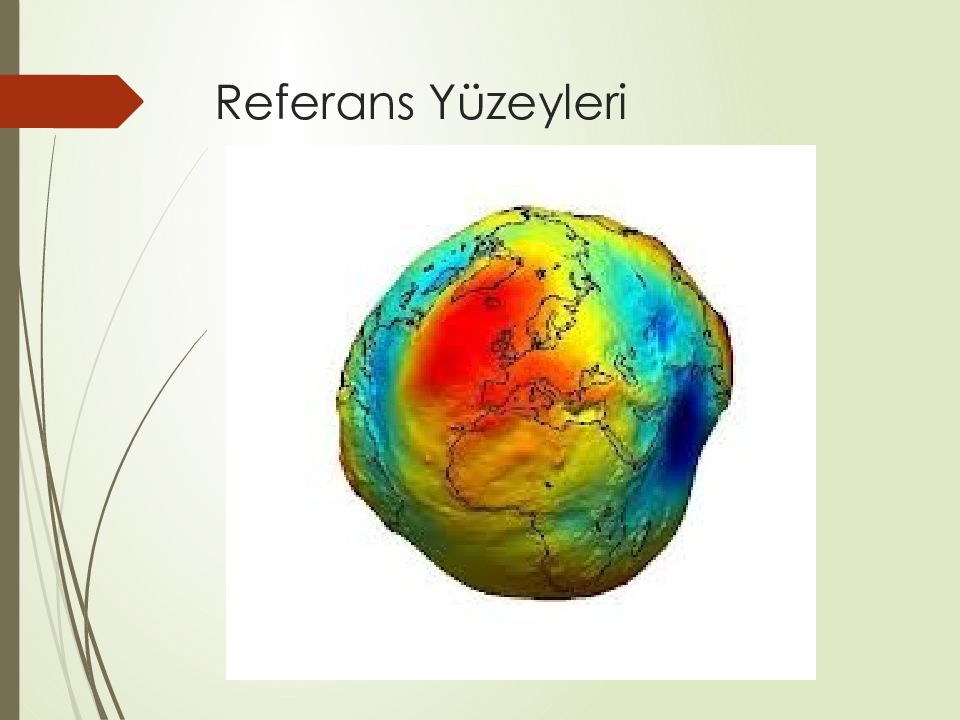
Jeodezinin tanımı incelendiğinde geometrik (yeryuvarının biçimi) ve fiziksel ( gravite alanı) olarak yeryuvarının tanımlanması soruları karşımıza çıkmaktadır. Yeryuvarının biçimi deyince fiziksel ve matematiksel yeryüzü anlaşılır. Fiziksel yeryüzü; katı ve sıvı yer kütlelerinin atmosfer karşısındaki sınırıdır. Benzer şekilde deniz dibi de katı yeryuvarı ile okyanus su kütleleri arasında bir sınır yüzeyi olarak jeodezik çalışmalar içerisindedir (Deniz Jeodezisi). Katı yeryuvarının düzensiz oluşmuş yüzeyi (kıtalar ve deniz dibi) basitçe matematik bir ilişki ile gösterilemez. Okyanus yüzeyi (yer yüzeyinin ≈70%) daha düzgün dağılımlı (durağan) kabul edilir.
Слайд 20: Referans Yüzeyleri
Gauss (1828) yeryuvarının şeklini “ Yeryuvarının geometrik anlamdaki yüzeyi denilen şey, öyle bir yüzeydir ki; gravite vektörü doğrultusunu her yerde dik keser ve tüm deniz yüzeyi bundan bir parçadır ” şeklinde tanımlamıştır. Daha sonra Listing (1873); Gauss’ un tanımladığı bu yüzeye Jeoit adını vermiştir: “ Kısmen okyanus yüzeyi ile gösterilebilen, daha önce yeryuvarının matematiksel yüzeyi olarak tanımlanan yüzeye, yeryuvarının jeoidal yüzeyi ya da kısaca jeoit diyeceğiz.”
Слайд 22
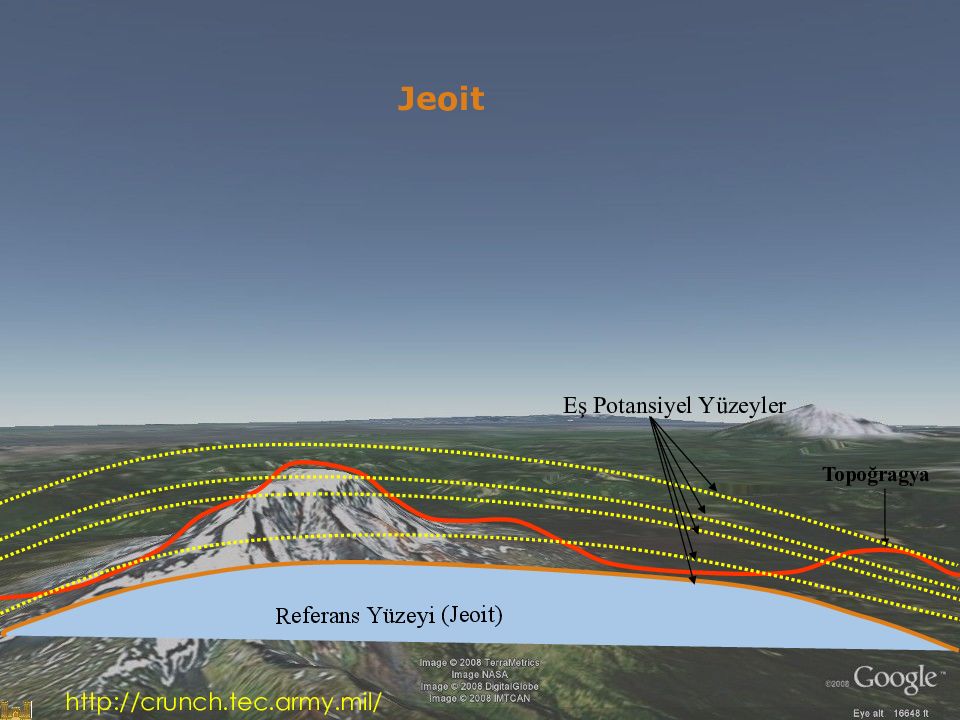
Eş Potansiyel Yüzeyler Referans Yüzeyi ( Jeoit ) Topo ğragya J eoi t http://crunch.tec.army.mil/
Слайд 23: Referans Yüzeyleri
Eş Potansiyel Yüzey: Eşit potansiyele sahip noktaların oluşturduğu yüzeydir. Çekül eğrisi (ya da gravite doğrultusu) bu yüzeylere dik ve bu yüzeyler birbirine paralel değildir. Gravite değerlerinin daha güçlü olduğu kutba yakın bölgelerde eş potansiyelli yüzeyler birbirine daha yakındır.
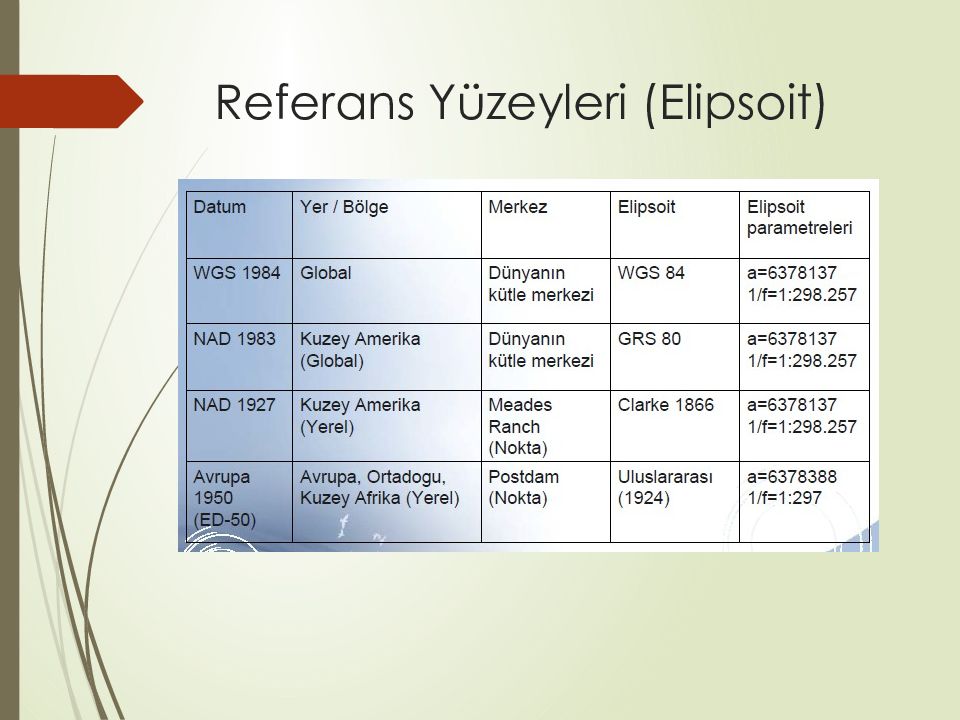
Слайд 24: Referans Yüzeyleri (Elipsoit)
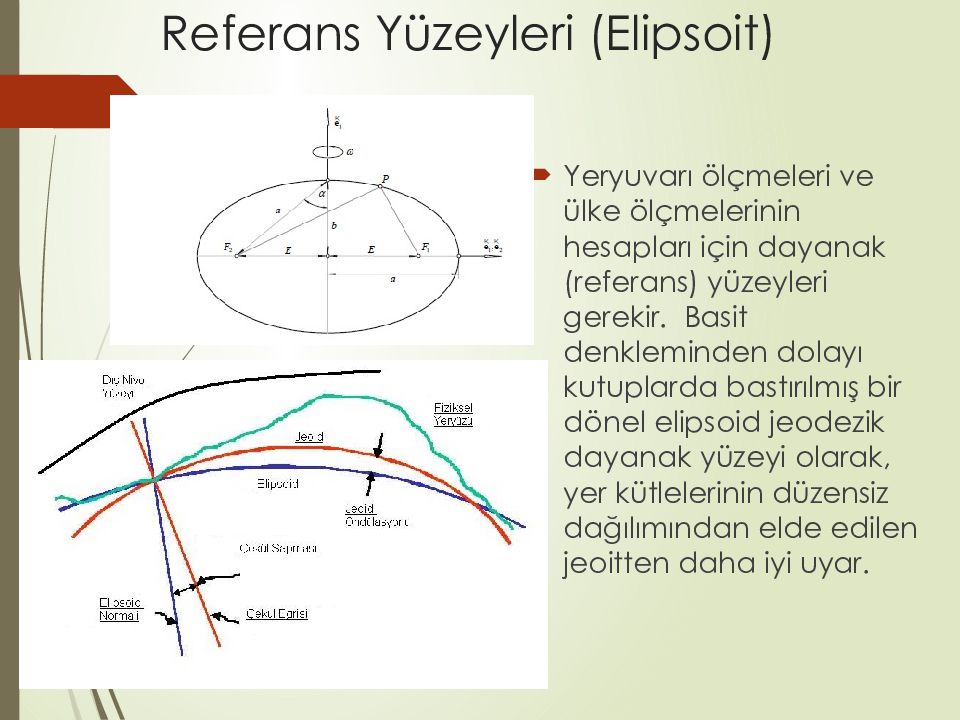
Yeryuvarı ölçmeleri ve ülke ölçmelerinin hesapları için dayanak (referans) yüzeyleri gerekir. Basit denkleminden dolayı kutuplarda bastırılmış bir dönel elipsoid jeodezik dayanak yüzeyi olarak, yer kütlelerinin düzensiz dağılımından elde edilen jeoitten daha iyi uyar.
Слайд 25: Referans Yüzeyleri (Elipsoit)
Yeryuvarı için tanımlı pek çok elipsoit bulunmaktadır. İhtiyaca ve bölgeye göre yeryuvarının fiziksel yüzeyi jeoide en iyi uyan elipsoidin seçilmesi oldukça önemlidir. Yeryuvarına boyut ve konum olarak en iyi uyan elipsoidin belirlenmesi jeodezinin önemli konularından birisidir. Elipsoidin belirlenmesi ile yeryuvarı matematiksel olarak modellenebilmektedir.
Слайд 26
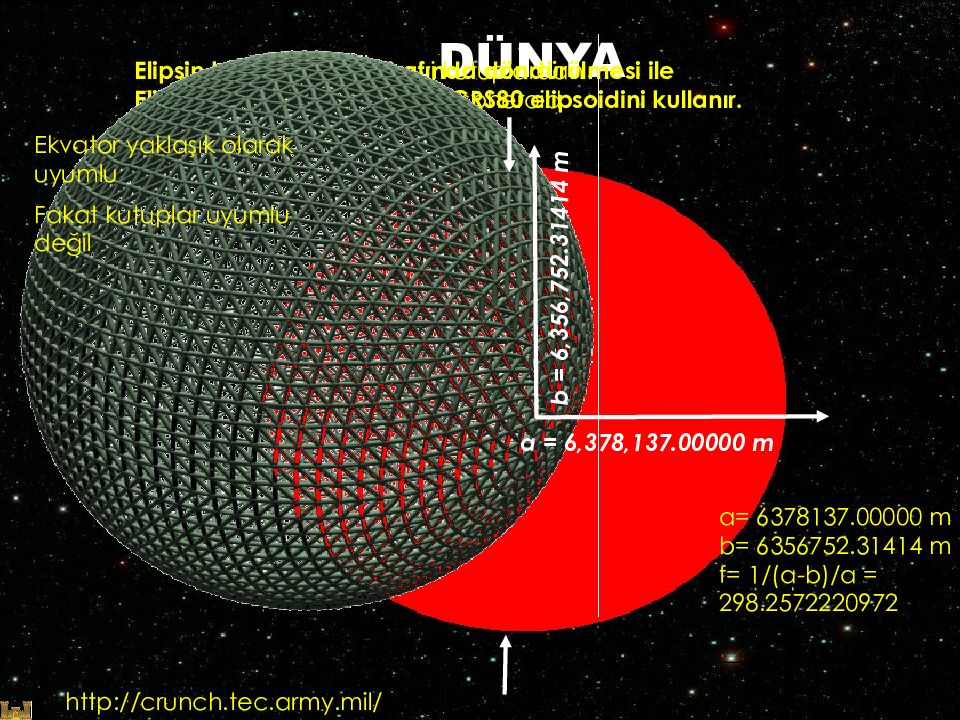
DÜNYA Elipsin küçük ekseni etrafında döndürülmesi ile Elipsoid oluşur. ITRF sistemi GRS80 elipsoidini kullanır. a= 6378137.00000 m b= 6356752.31414 m f= 1/(a-b)/a = 298.2572220972 Eğer Küreyi kutuplardan bastırırsak bir spheroid oluştururz. a = 6,378,137.00000 m b = 6,356,752.31414 m Ekvator yaklaşık olarak uyumlu Fakat kutuplar uyumlu değil http://crunch.tec.army.mil/
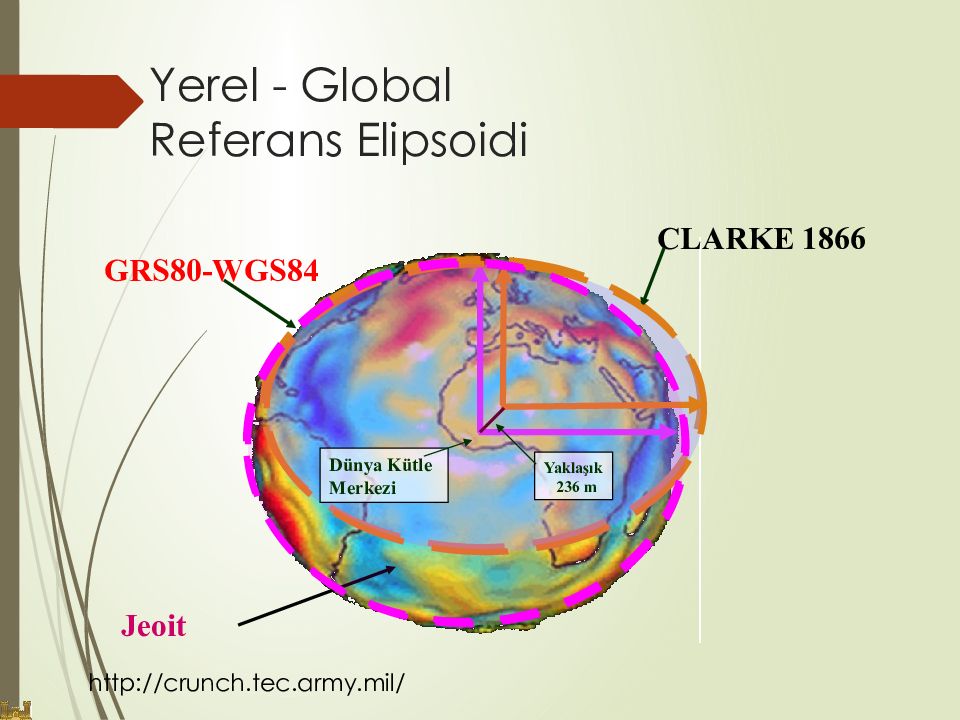
Слайд 28: Yerel - Global Refer ans Elipsoid i
GRS80-WGS84 CLARKE 1866 Jeoit Dünya Kütle Merkezi Yaklaşık 236 m http://crunch.tec.army.mil/
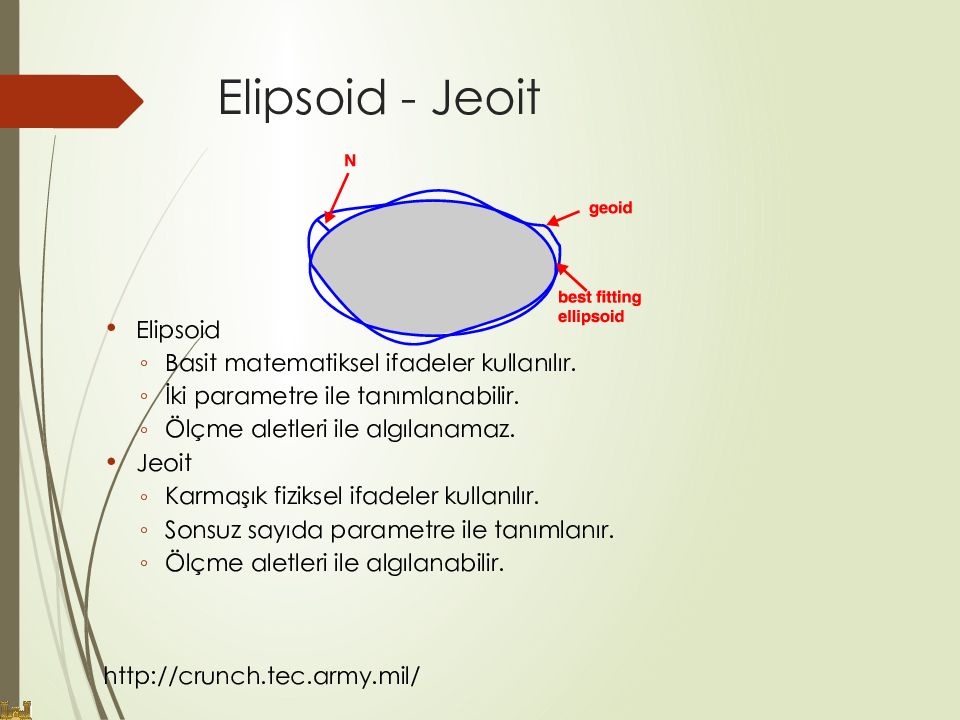
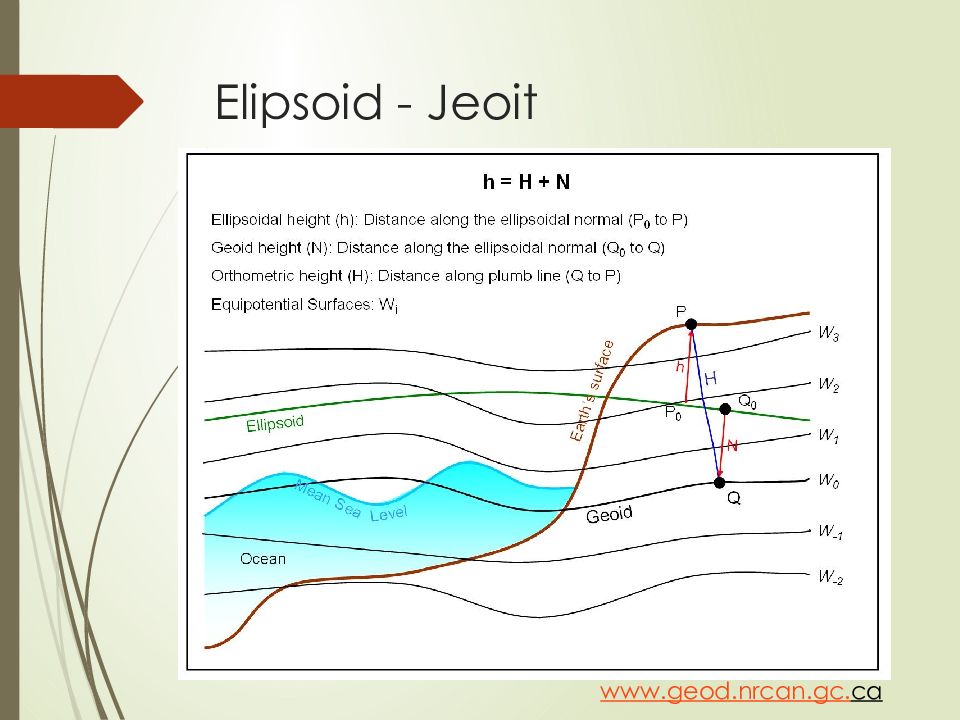
Слайд 30: Elipsoid - J eoi t
Elipsoid Basit matematiksel ifadeler kullanılır. İki parametre ile tanımlanabilir. Ölçme aletleri ile algılanamaz. Jeoit Karmaşık fiziksel ifadeler kullanılır. Sonsuz sayıda parametre ile tanımlanır. Ölçme aletleri ile algılanabilir. http://crunch.tec.army.mil/
Слайд 37: Fundamental Stations - Collocation of All Techniques - including Gravity
Wettzell, Germany, one of only six fundamental stations
Слайд 38: Ülke Temel Ağları
Çeşitli amaçlar için yeryüzü üzerinde sabit noktalar ağı oluşturulmaktadır. Amaca göre bu ağlar düşey kontrol ağı ( nivelman ağı) yada yatay kontrol ağı (nirengi ağı) şeklinde tasarlanmaktadır. Bir yatay kontrol ağında yalnızca kenar ölçülürse bu ağa trilaterasyon ağı, ölçek için an az bir kenar ölçülmek koşuluyla yalnız açı ölçüleri yapılırsa triyangülasyon ağı denir. Düşey kontrol ağlarında temel yüzey olarak jeoid alınsa da, jeoidin geometrik biçimi ne düzlem, ne küre, ne de dönel elipsoid olarak kabul edilebilir. Yatay kontrol ağlarında büyüklüğü ve biçimi yer yuvarına yakın bir dönel elipsoid seçilir. Tümüyle yapay olan bu elipsoid yeryuvarı ile hemen hemen aynı olacak şekilde uzaya yerleştirilir. Ağı oluşturan yeryüzü noktaları büyüklüğü (büyük yarıçapı), biçimi (basıklığı) ve uzaydaki konumu keyfi olarak seçilen bu dönel elipsoidin yüzüne izdüşürülür. Bu izdüşüm noktalarının elipsoid üzerindeki boylam ve enlem değerleri yatay kontrol noktalarının koordinatlarını oluşturur.
Слайд 40: Ülke Temel Ağları
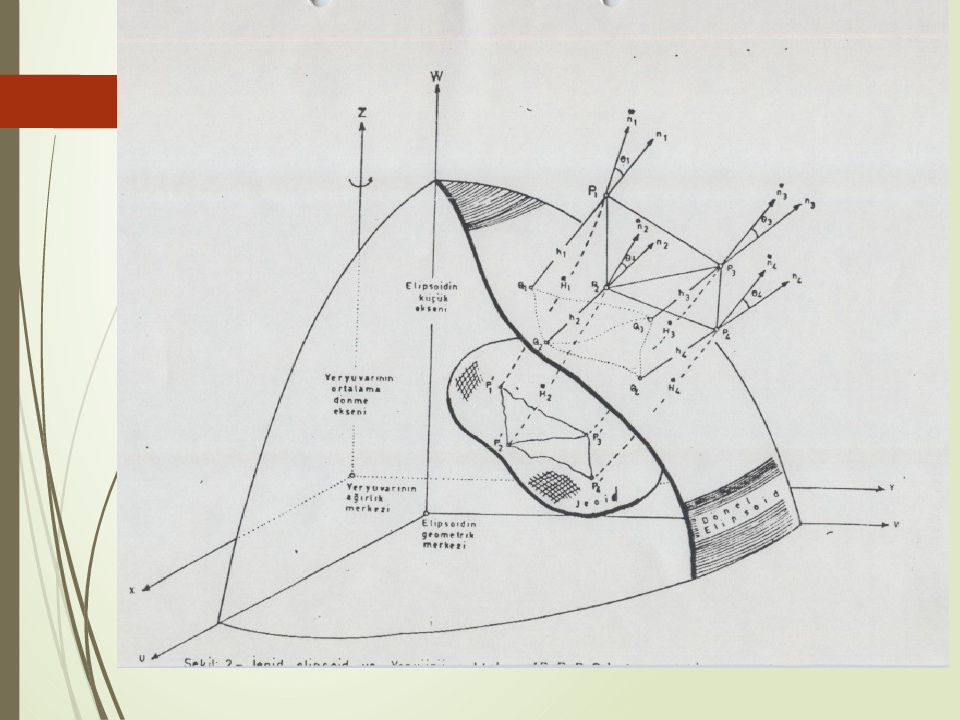
Şekildeki X, Y, Z dik koordinat sistemi tümüyle katı yer yuvarına bağlıdır ve doğa içinde mevcuttur. Buna karşın u, v, w sistemi tümüyle dönel elipsoide bağlıdır ve soyuttur. Kuramsal jeodezide, dönel elipsoidin boyutlarının seçimine “ Elipsoid Problemi ”, onun katı yeryuvarına göre uzayda belirli bir konuma yerleştirilmesine “ Datum Problemi ” denir. “ Hayford Elipsoidi”, “ Bessel Elipsoidi”, “ Clark Elipsoidi” elipsoidlerin yalnızca boyutlarını tanımlar. “Avrupa Datumu 1950”, “Kuzey Amerika Datumu 1927” elipsoidlerin yalnız uzaydaki konumlarını tanımlar. İdeal olarak X, Y, Z eksenleri ile u, v, w eksenlerinin özdeş olması beklenir, günümüz teknolojisi ile bu çok küçük farklılıklarla sağlanmaktadır.
Слайд 41: Ülke Temel Ağları
Türkiye'ye ait ülke triyangülasyon ağına altlık teşkil eden elipsoidin parametreleri Hayford Elipsoidi boyutları seçilmiştir. Bu elipsoid önce Ankara civarındaki I. Derece noktalardan Meşedağı ’ ndaçekül sapması sıfır kabul edilmek üzere ve Duatepe noktasına olan astronomik azimut Laplace azimutu kabul edilerek uzayda yerleştirilmiştir. Bu şekilde “ulusal datum ” tanımlanmıştır. Ayrıca orta Avrupa’ da Herlmert Kulesi Turm noktasında çekül sapmasının doğu-batı bileşeni +1.78” ve kuzey- guney bileşeni +3.36”olacak şekilde boyutları Hayford Elipsoidi olacak şekilde başka bir elipsoid oluşturulmuş ve elipsoidin bu konumuna “Avrupa Datumu 1950” denmiştir. Bulgaristan ve Yunanistan’ daki sekiz adet noktadan hesap yapılarak Türkiye Ulusal Datumundaki koordinatlar hesaplanmıştır. Ülke triyagülasyon ağını oluşturan noktalar yeryüzü işaretleri, gözlemelrin nitelik ve niceliği ve hesaplamalarındaki yöntemler bakımından dört derecede ele alınmıştır.
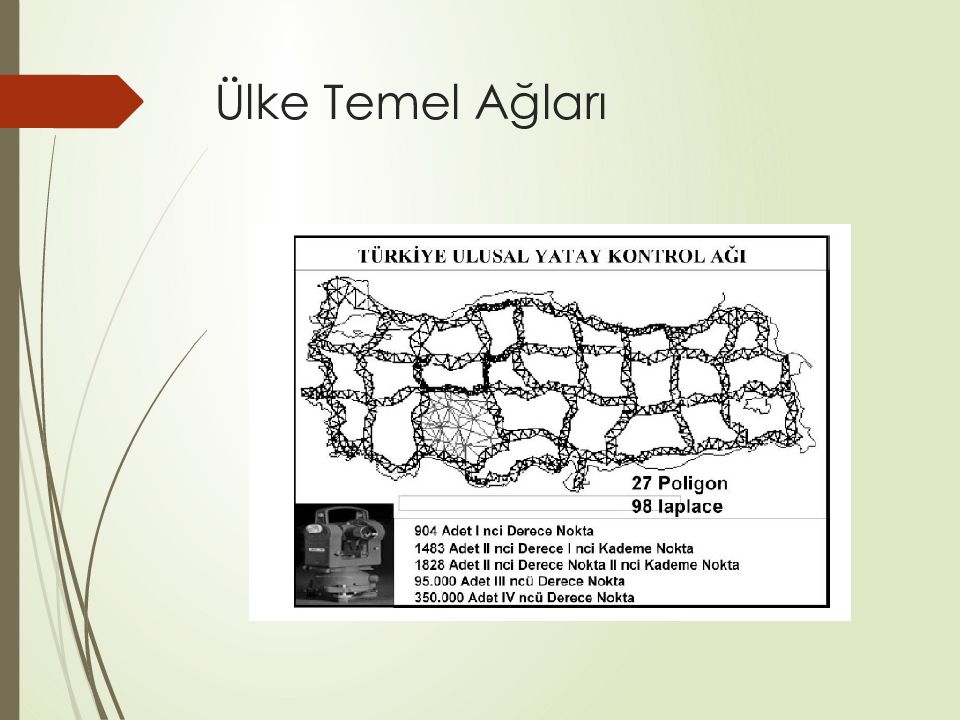
Слайд 43: Ülke Temel Ağları
Birinci Derece Noktalar: kuzey-güney ve doğu-batı doğrultularındaki zincirlerin çevrelediği poligonlar biçimindedir. 98 adet noktada astronomik gözlemler, enlem, boylam ve azimut belirlenmiş, 40 adet baz ölçüsü yapılmış, doğrultu ölçmeleri 24 dizi gerçekleştirilmiştir. Doğrultu ölçmelerine, çekül sapması bileşenlerinden dolayı olanların dışında, her türlü indirgeme, elipsoid yüksekliği yerine ortometrik yükseklikler alınarak uygulanmıştır. Bazların indirgenmesinde de elipsoidal yükseklikler yerine ortometrik yükseklikler kullanılmıştır. Elipsoid yüzüne indirgenmiş ölçülerin dengelemesi dolaylı ölçüler dengelemesi yöntemiyle gerçekleştirilmiştir. Dengelemenin düzlemde yapılması amacıyla yeryüzünden elipsoide indirgenmiş ölçüler, bu kez elipsoidden Lambert-Konik projeksiyonuna aktarılmıştır. Dengelemede Laplace azimutları ve Meşedağ noktasının astronomik gözlemlerle belirlenen enlem ve boylam değeri sabit tutulmuştur. I. Derece Yatay Kontrol Ağı, Türkiye Ulusal Datumu – 1954 (TUD-54) olarak bilinir.
Слайд 44: Ülke Temel Ağları
İkinci Derece Noktalar: Bu noktalar, Türkiye’ nin bütününde I. Derece noktaların oluşturduğu zincirler arasında ve poligonların ortasında boş alanları doldurmak, hem de nokta sıklığı sağlamaktır. Üçüncü Derece Noktalar: Bu noktalar, IV. Derece noktaların tesisi için nokta sıklığını sağlamaktır. Dördüncü Derece Noktalar: Bu noktalar detay alımını sağlayacak şekilde ağı yoğunlaştırmak üzere atılır. Genellikle üzerlerine alet kurulmaz ve önden kestirme ile hesaplanır. Ülke triyangülasyon ağını oluşturan noktaların yatay koordinatları, Avrupa Datumu 1950’ deki elipsoid koordinatları ile 3-6 derecelik dilim genişliklerinde Gauss- Kruger koordinatları biçimindedir.
Слайд 45: Ülke Temel Ağları
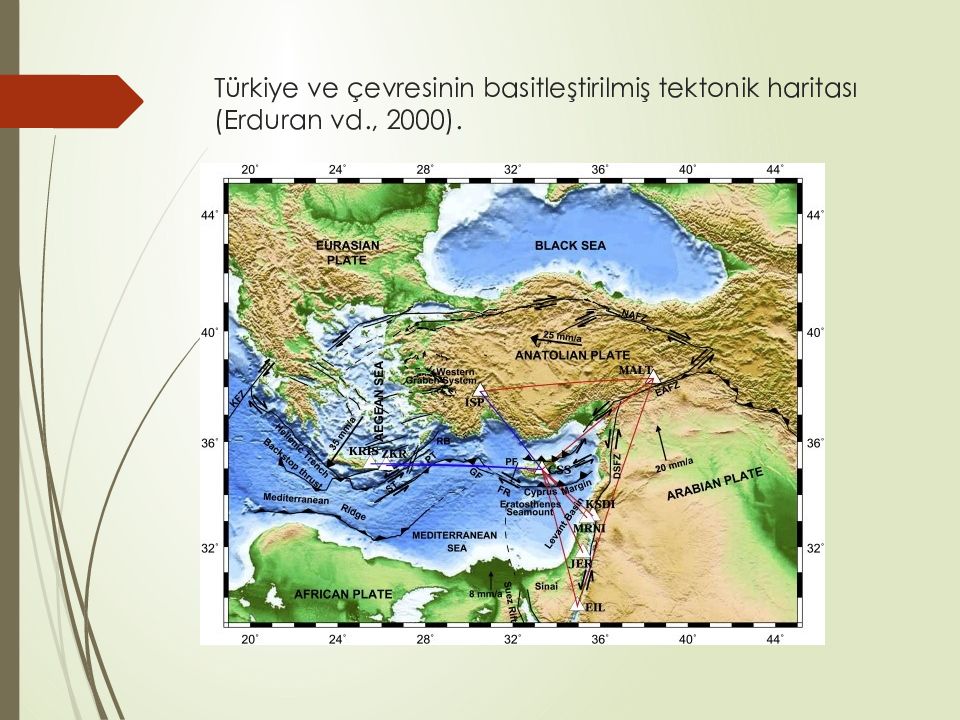
Türkiye bulunduğu konum itibariyle Afrika, Arap ve Avrasya plakalarının çarpıştığı bir bölgede bulunmaktadır. Özellikle Kuzey Anadolu Fay Zonu (KAFZ), Doğu Anadolu Fay Zonu (DAFZ) ve Ege Graben Sistemi’ nde meydana gelen depremler sonucunda TUD-54 noktalarında büyüklük ve yönü bölgeden bölgeye değişen en çok ± 3-5 m mertebesinde yatay konum değişiklikleri olduğu düşünülmektedir. Düşey konum değişikleri deprem yüzey kırığı çevresinde 1-3 m değerlerine ulaşmakta ve yüzey kırığından uzaklaştıkça azalmaktadır.
Слайд 46: Türkiye ve çevresinin basitleştirilmiş tektonik haritası ( Erduran vd., 2000)
Слайд 47: Ülke Temel Ağları
Meydana gelen deformasyonlar sonucunda bölgesel ve yerel nitelikte yatay ve düşey konum değişiklikleri meydana geldiği ve TUD-54’ ün pratik kullanım ihtiyaçlarına cevap vermekten uzaklaştığı belirlenmiştir. Meydana gelen bu deformasyonlar ve Global Konumlama Sistemlerindeki (GPS) gelişmelere paralel olarak, yeni bir jeodezik temel ağ oluşturulması ihtiyacı doğmuştur. Bu ağın; GPS teknolojisine dayalı, Üç boyutlu jeosentrik koordinat sisteminde, belirli bir zamanda ( epok ), her noktasında koordinat ((X,Y,Z) veya (enlem, boylam, elipsoid yüksekliği)), hız (( V x, V y, V z ) veya (V ϕ, V λ, V h )) ortometrik yükseklik (H) ve jeoid yüksekliği (N) bilinen, Ülke yüzeyine olabildiğince homojen dağılmış, ulaşımı kolay ve birbirini görme zorunluluğu olmayan noktalardan oluşan, Jeodezik konum belirleme, navigasyon ve jeodinamik amaçlarla kullanıma uygun, ED-50 datumundaki Ulusal Temel Yatay Kontrol Ağı ile arasında dönüşümü sağlanan bir ağ olması öngörülmüştür.
Слайд 48: Ülke Temel Ağları
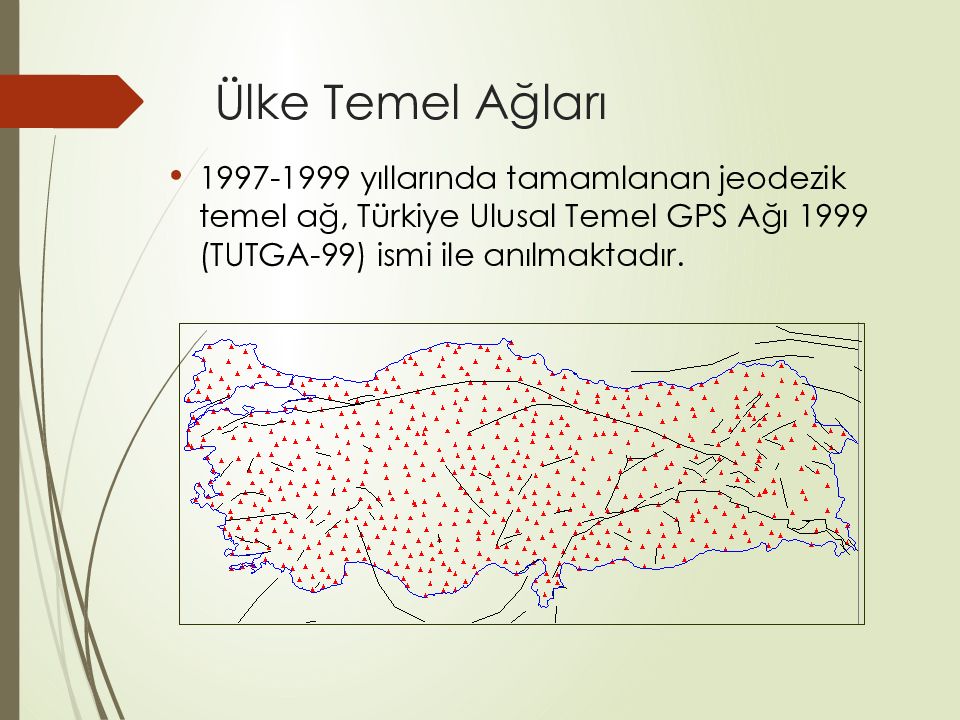
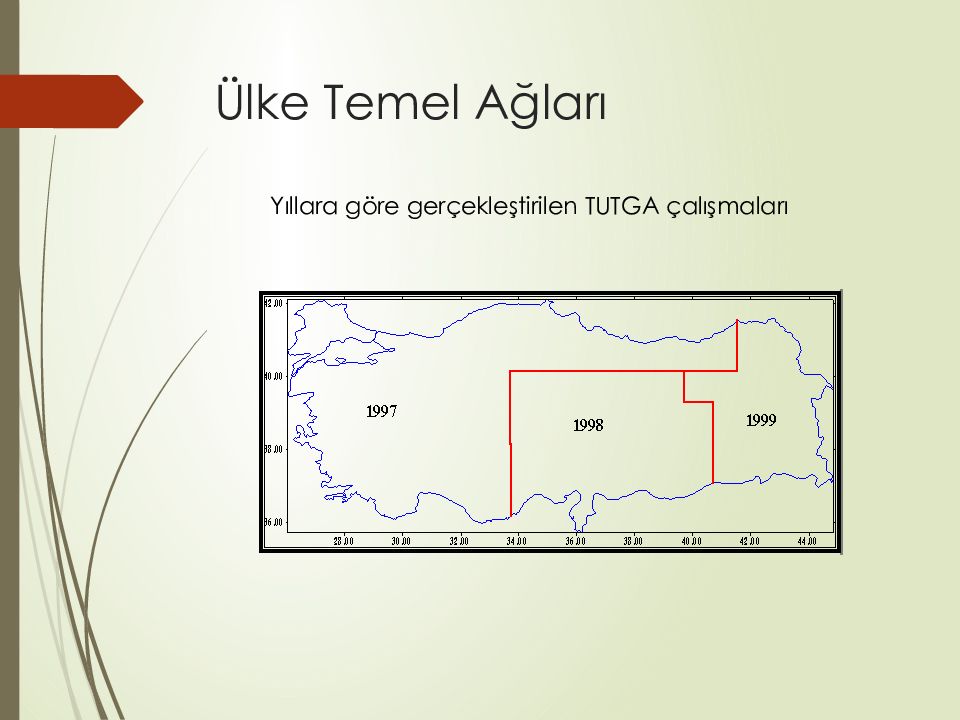
1997-1999 yıllarında tamamlanan jeodezik temel ağ, Türkiye Ulusal Temel GPS Ağı 1999 (TUTGA-99) ismi ile anılmaktadır.
Слайд 50: Ülke Temel Ağları
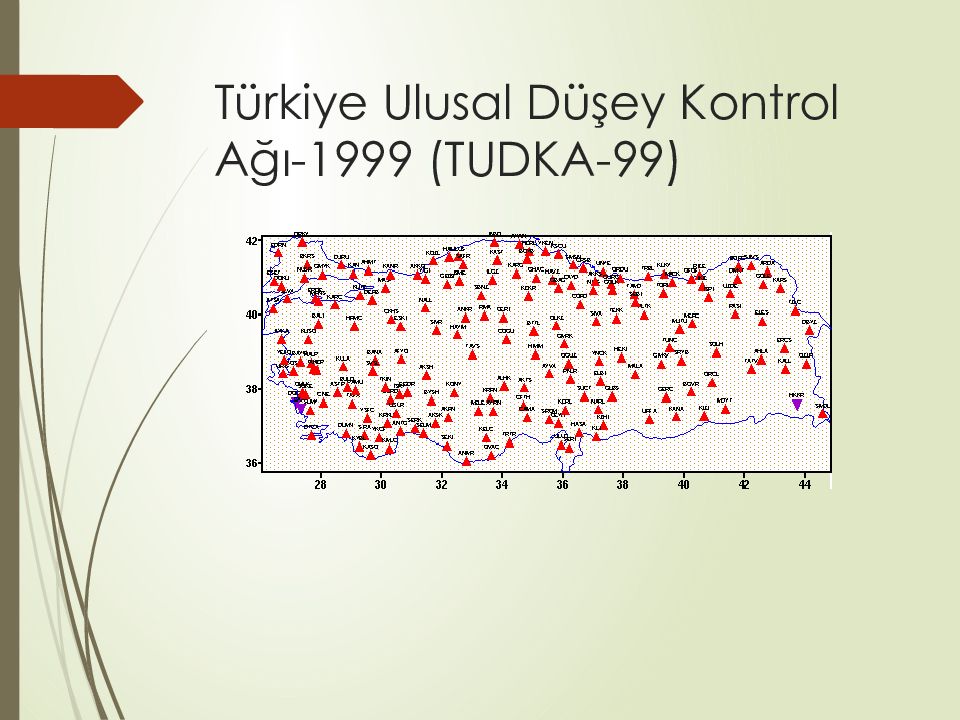
TUTGA-99 beş ana elemandan oluşur: Uluslar arası Yersel Referans Sistemi-1996 (ITRF-96)’ da, 1998.0 epoklu koordinatları bilinen GPS Ağı. TUTGA-99 Hız Alanı. TUTGA-99 ile ED-50 arasında Koordinat Dönüşümü. Her noktasında Helmert Ortometrik Yüksekliği bilinen Türkiye Ulusal Düşey Kontrol Ağı-1999 (TUDKA-99) Türkiye Jeoidi -1999 (TG-1999)
Слайд 51: Ülke Temel Ağları
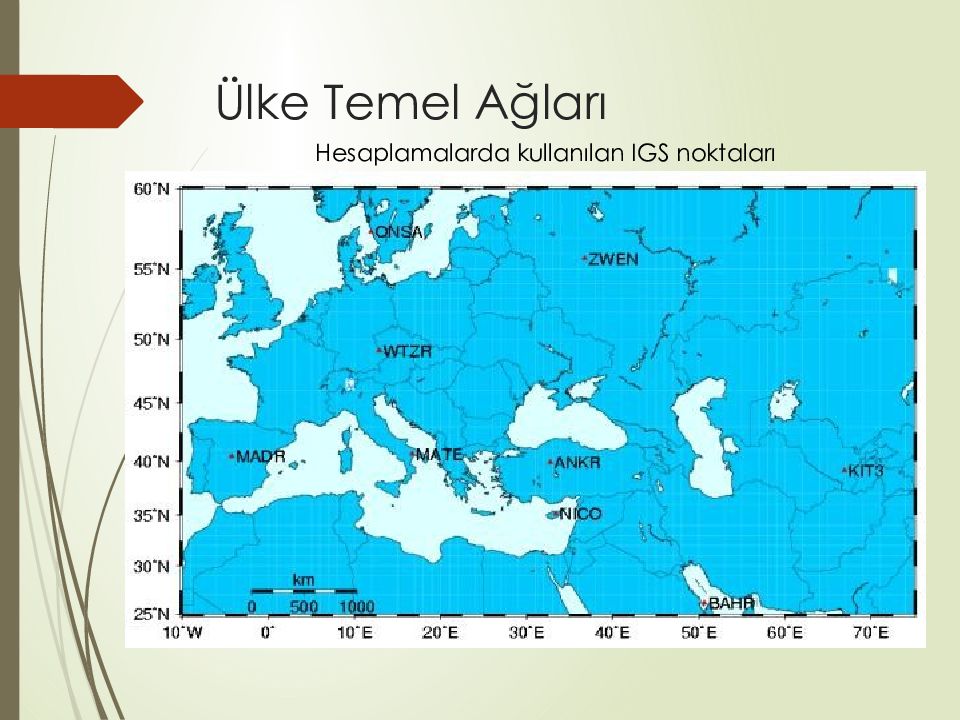
Planlama çalışmalarında TUTGA’ yı oluşturan noktalar üç grupta toplanır: Eski noktalar: Daha önceden tesis edilmiş noktalar olup, I. ve II. Derece Yatay Kontrol Ağı ile I. ve II. Derece Düşey kontrol ağı noktalarından seçilenler, SLR ( Satellite Laser Ranging ) noktaları ve mevcut GPS noktalarından uygun dağılımı sağlayanlar. Yeni noktalar: Proje kapsamında yeni tesis edilen aralarındaki uzaklıkları tek ve çift frekanslı GPS alıcıları ile nokta sıklaştırması ve DGPS uygulamaları için 25-50 km’ de bir, jeoidin hızlı değiştiği bölgelerde 15 km’ de bir seçilen noktalardır. Global noktalar: TUTGA’ nın ITRF referans sisteminde tanımını gerçekleştirmek amacıyla Türkiye ve yakın çevresinde, Avrupa ve Asya’ da uygun dağılımdaki IGS ( International GPS Service) noktalarıdır. Arazi çalışmaları kapsamında noktaların keşif ve seçimi, yer noktası inşaatı ve GPS ölçüsü yapılmıştır. Hesaplama Çalışmalarında: TUTGA noktalarında yapılan GPS ölçüleri BERNESE ve GLOBK akademik yazılımları ile değerlendirilmiştir.
Слайд 53: Ülke Temel Ağları
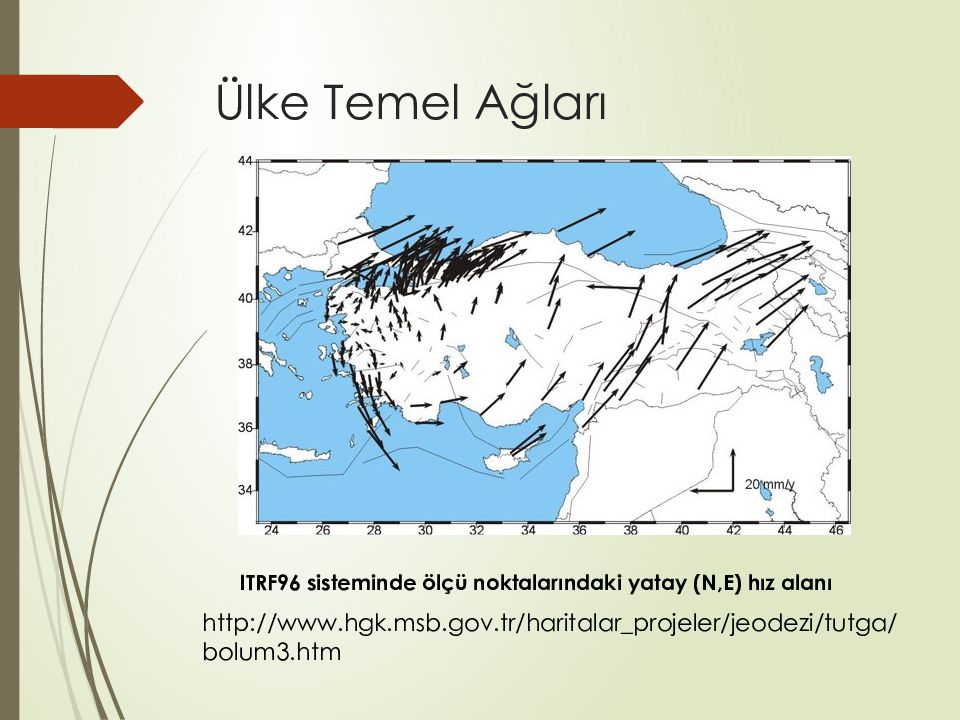
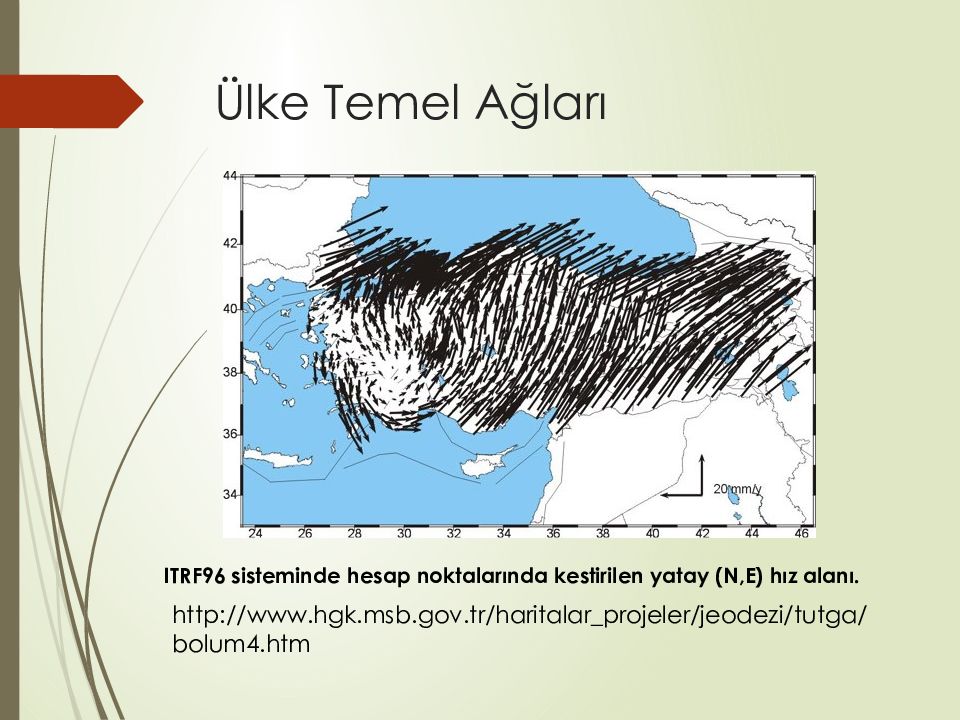
ITRF96 sisteminde ölçü noktalarındaki yatay (N,E) hız alanı http://www. hgk. msb.gov.tr/haritalar_projeler/jeodezi/ tutga /bolum3. htm
Слайд 54: Ülke Temel Ağları
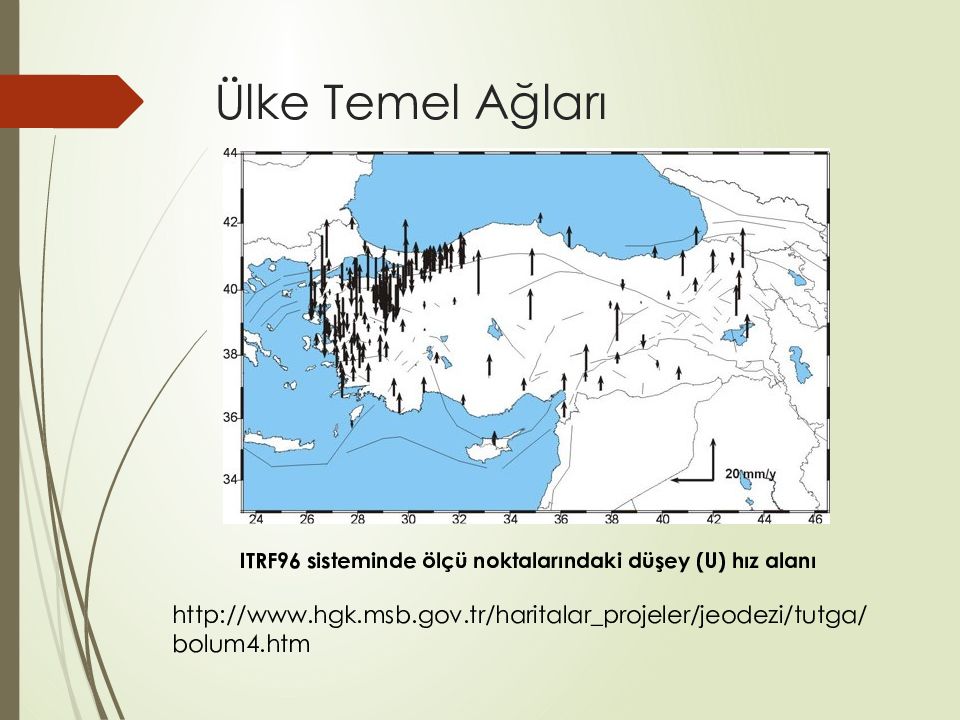
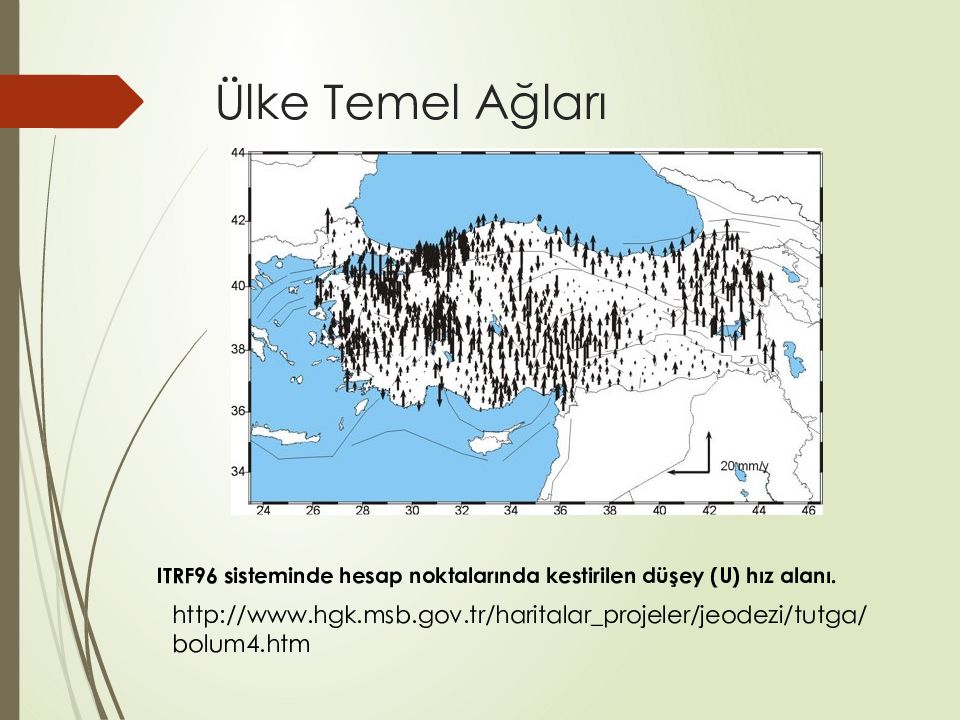
ITRF96 sisteminde ölçü noktalarındaki düşey (U) hız alanı http://www. hgk. msb.gov.tr/haritalar_projeler/jeodezi/ tutga /bolum4. htm
Слайд 55: Ülke Temel Ağları
ITRF96 sisteminde hesap noktalarında kestirilen yatay (N,E) hız alanı. http://www. hgk. msb.gov.tr/haritalar_projeler/jeodezi/ tutga /bolum4. htm
Слайд 56: Ülke Temel Ağları
ITRF96 sisteminde hesap noktalarında kestirilen düşey (U) hız alanı. http://www. hgk. msb.gov.tr/haritalar_projeler/jeodezi/ tutga /bolum4. htm
Слайд 57: Ülke Temel Ağları
17 Ağustos 1999 İzmit ( Mw =7.5), 12 Kasım 1999 ( Mw =7.2) ve 6 Haziran 2000 Çerkeş/Çankırı ( Mw =6.1) depremleri TUTGA-99 nokta koordinatlarında önemli miktarlarda değişiklikler meydana getirmiştir. TUTGA-99 koordinatları ve depremler öncesi inter -sismik hız alanı kullanılarak 17 Ağustos 1999 (1999.62) sonrasında koordinat hesaplamak olanaksız hale gelmiştir. Depremler sonrası ölçülen 12 adet GPS kampanyasını birleştirip deprem sonrası nokta koordinatlarını elde etmek mümkün olmuştur, deprem bölgesi dışındaki tüm tekrarlı ölçüleri kullanmak için 1992-2001 yılları ölçülen toplam 35 GPS (23 adet deprem öncesi-12 adet deprem sonrası) kampanyası topluca GLOBK yazılımı ile birleştirilerek TUTGA-99A tanımlanmıştır.
Слайд 58: Ülke Temel Ağları
TUTGA-99A 1998.0 epoklu, homojen ve yüksek doğruluktadır. GPS ile TUTGA-99A’ ya dayalı olarak sıklaştırmada zaman boyutu dikkate alınmalı ve nokta koordinatları Referans Epoğuna (T0=1998.0) kaydırılmalıdır. Bu işlem sıklaştırma noktalarının depremden etkilenen bölge içinde olup olmamasına göre farklılık gösterir. http://www.harita. selcuk.edu.tr/ arsiv /calistay2003/01OLenk_ CDemir. pdf
Слайд 60: TUTGA-99 ile ED-50 arasındaki dönüşüm
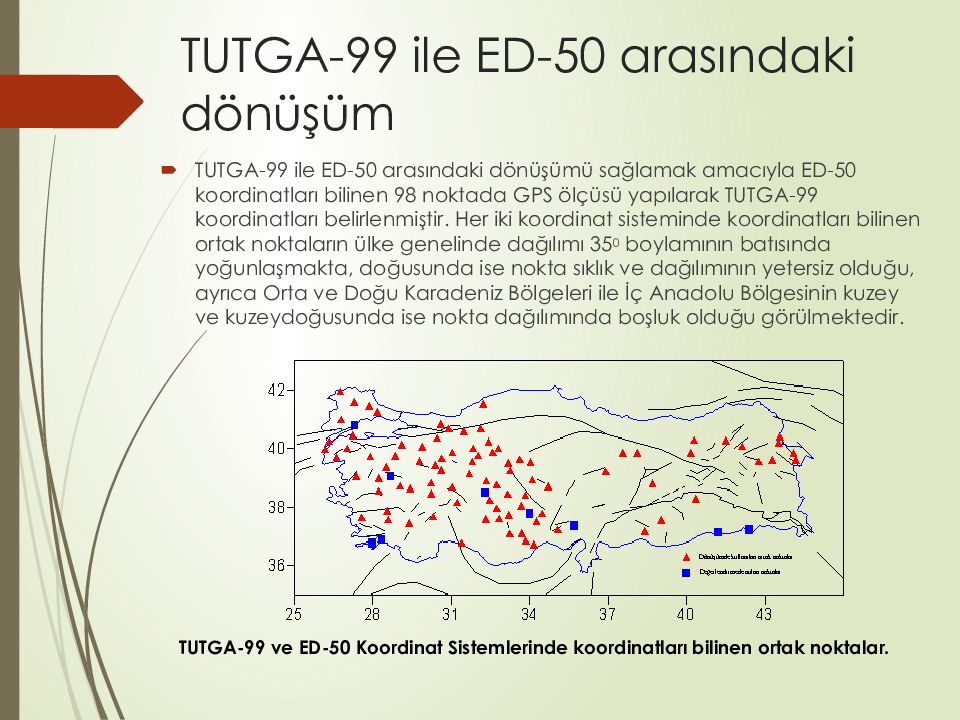
TUTGA-99 ile ED-50 arasındaki dönüşümü sağlamak amacıyla ED-50 koordinatları bilinen 98 noktada GPS ölçüsü yapılarak TUTGA-99 koordinatları belirlenmiştir. Her iki koordinat sisteminde koordinatları bilinen ortak noktaların ülke genelinde dağılımı 35 0 boylamının batısında yoğunlaşmakta, doğusunda ise nokta sıklık ve dağılımının yetersiz olduğu, ayrıca Orta ve Doğu Karadeniz Bölgeleri ile İç Anadolu Bölgesinin kuzey ve kuzeydoğusunda ise nokta dağılımında boşluk olduğu görülmektedir. TUTGA-99 ve ED-50 Koordinat Sistemlerinde koordinatları bilinen ortak noktalar.
Слайд 61: TUTGA-99 ile ED-50 arasındaki dönüşüm
Bu iki koordinat sistemi arasında dönüşümü incelemeden önce ortak noktalarda TUTGA-99 ve ED-50 koordinatlarının birbirinden farklı olmasının geometrik ve fiziksel nedenleri aşağıda ele alınmaktadır. a. Geometrik nedenler: Yeni oluşturulan TUTGA-99, ITRF96 üç boyutlu, jeosentrik koordinat sisteminde, GRS-80 Elipsoidine göre GPS ölçüleri ile oluşturulmuş, halen kullanılmakta olan ED50 ise yersel ölçüler (açı, baz, astronomik enlem, astronomik boylam, astronomik azimut) ile Uluslararası Elipsoid ve farklı bir üç boyutlu koordinat sisteminde tanımlıdır. Elipsoid ve koordinat sistemleri ( datum ) birbirinden farklı olduğu için öncelikle bu iki koordinat sistemi arasında kayıklık, dönüklük ve ölçek farklılığı beklenmektedir ( Rapp, 1976). Ulusal Temel Yatay Kontrol(Nirengi) Ağının hesabında ölçülere uygun indirgemelerin getirilememesi, uygulanan dengeleme yöntemi ve koordinat sistemi tanımından kaynaklanan sistematik karakterli ağın tamamını etkileyen bozukluklar bulunmaktadır(AMS, 1954, Sarbanoğlu vd., 1979). Tokyo Datumunda yapılan uygulamada jeoidin ihmal edilmesi nedeniyle 2-6 ppm, çekül sapmaları nedeniyle indirgemelerin yapılmaması ise 1-2 ppm lik ağın tamamında sistematik bozukluk yaratmaktadır ( Komaki, 1985). Yersel ölçülere getirilecek indirgemeler Müller (1974), Vanicek ve Krakiwsky (1986), Sideris (1990) de incelenmekte olup Kanada Temel Ağındaki etkileri Thomson vd. (1974) incelenmiş ve sistematik etkileri gösterilmiştir. ED-50‘ye dönüşüm yöntemi ve bu dönüşümde kullanılan Yunanistan ve Bulgaristan sınırları içinde seçilen 8 ortak noktanın dağılımından kaynaklanan sistematik etkiler ( Sarbanoglu vd., 1979).
Слайд 62: TUTGA-99 ile ED-50 arasındaki dönüşüm
Bu iki koordinat sistemi arasında dönüşümü incelemeden önce ortak noktalarda TUTGA-99 ve ED-50 koordinatlarının birbirinden farklı olmasının geometrik ve fiziksel nedenleri aşağıda ele alınmaktadır. b. Fiziksel nedenler: Ulusal Temel Yatay Kontrol(Nirengi) Ağının kurulmaya başlandığı 1934 ile 1999 yılları arasında, KAFZ, DAFZ, Ege Graben Sistemi ve Doğu Anadolu Bölgesinde büyüklüğü M w 6.0 olan çok sayıda deprem olmuş ve bu depremler sırasında 2-3 metre yatay, 3 metre düşey yönlü konum değişiklikleri ( ko -sismik) olmuştur. Ko -sismik konum değişiklikleri sonucu Ulusal Temel Yatay Kontrol (Nirengi) Ağı noktalarında yerel ve bölgesel nitelikli bozulmalar oluşmuştur. Tektonik plaka hareketleri nedeniyle 1-1.5 metre büyüklüğündeki inter -sismik yatay yer değiştirmeler sonucu bölgesel karakterli ancak tektonik yapının karmaşık olduğu bölgelerde yerel özellikte konum bozuklukları beklenmektedir.
Слайд 63: TUTGA-99 ile ED-50 arasındaki dönüşüm
Burada, Δ X, Δ Y, Δ Z ötelemeler, R X, R Y ve R Z dönüklükler, Δ S ise ölçek farklılığıdır.
Слайд 64: TÜRKİYE JEOİDİ – 1991 ( TG-91 )
Türkiye Jeoidi –1991 (TG-91) adı ile bilinen gravimetrik jeoid, GPM2-T1 yer potansiyel katsayıları, topoğrafik yükseklikler ve gravite ölçüleri değerlendirilerek hesaplanmıştır.
Слайд 65: GPS/NİVELMAN JEOİDİ
GPS/ nivelman jeoid yüksekliklerini belirlemek için; Türkiye içinde uygun dağılımda, jeoidin hızlı değiştiği bölgelerde daha sık olmak üzere, 197 TUTGA-99 noktası seçilmiş ve geometrik nivelman ölçüleriyle Türkiye Ulusal Düşey Kontrol Ağı-1999 (TUDKA-99) ‘ na bağlanmıştır. Seçilen bu noktalardan ayrı olarak çeşitli mühendislik uygulamalarında kullanılmak üzere 122 GPS/ nivelman noktası daha oluşturulmuştur. Söz konusu 122 nokta hesaplanan jeoid modelinin dış kontrolu amacıyla kullanılacaktır. Toplam 197 GPS/ nivelman noktasının TUTGA-99 koordinat sisteminde elipsoid yükseklikleri ile TUDKA-99 datumunda geometrik nivelman ölçüleri ve gravite değerleri ile ortometrik yükseklikleri belirlenmiştir.
Слайд 66: DÜZENLENMİŞ TÜRKİYE JEOİDİ – 1999 (TG-99A)
Türkiye Ulusal Temel GPS Ağı’nın oluşturulması kapsamında gerçekleştirilmiş ve GPS/ Nivelman ve TG-91 jeoid modellerinin birleştirilmesi ile TG-99 oluşturulmuştur (Ayhan v.d., 2001). TG-99’un oluşturulmasında 187 nokta kullanılmıştır. Ayrıca, TG-99’un hesaplanmasında kullanılan 187 noktaya ek olarak, 3 adet kontrol ve 10 adet yeni GPS/ Nivelman noktasının da oluşturulması ile 197 nokta kullanılmakta olup hesaplanan yeni jeoid Düzenlenmiş Türkiye Jeoidi -1999 (TG-99A) olarak isimlendirilmiştir.
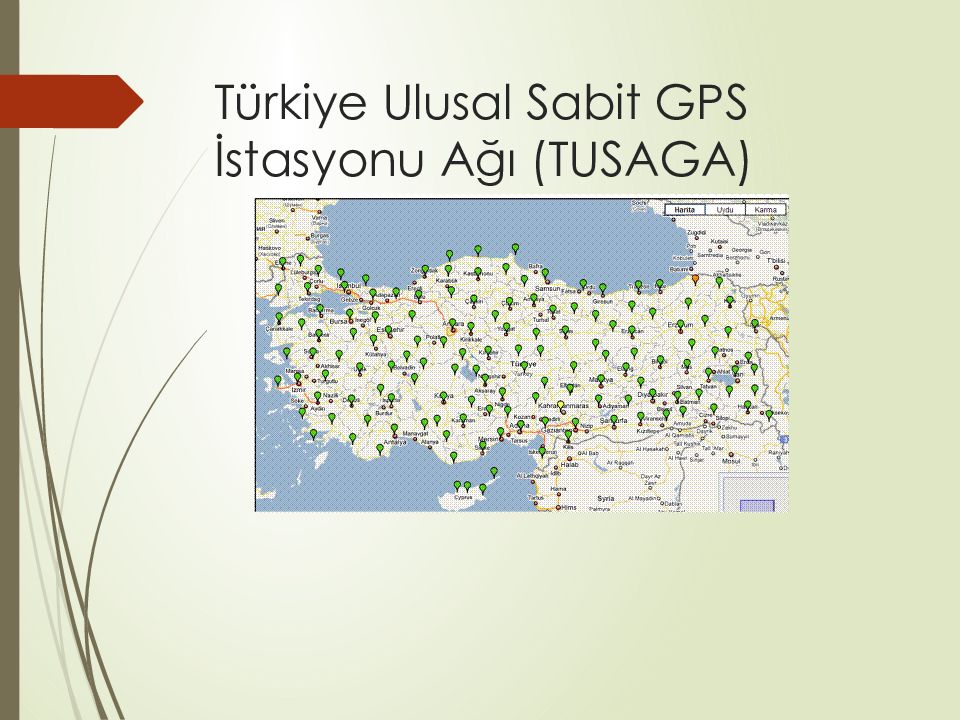
Слайд 67: Türkiye Ulusal Sabit GPS İstasyonu Ağı (TUSAGA)
Türkiye’ ye dağılmış IGS standartlarında noktalardan oluşacak ağ ile; Jeodezik çalışmalar için üst düzey nokta oluşturmak Bölgesel GPS ölçmelerinde master nokta olarak ; zaman, personel, alet ve maliyet tasarrufu yapmak, veri bağlantı kayıplarını önlemek, Tektonik aktiviteyi lzlemek, Gerçek zamanda Diferansiyel GPS hizmeti sunmak hedeflenmektedir.