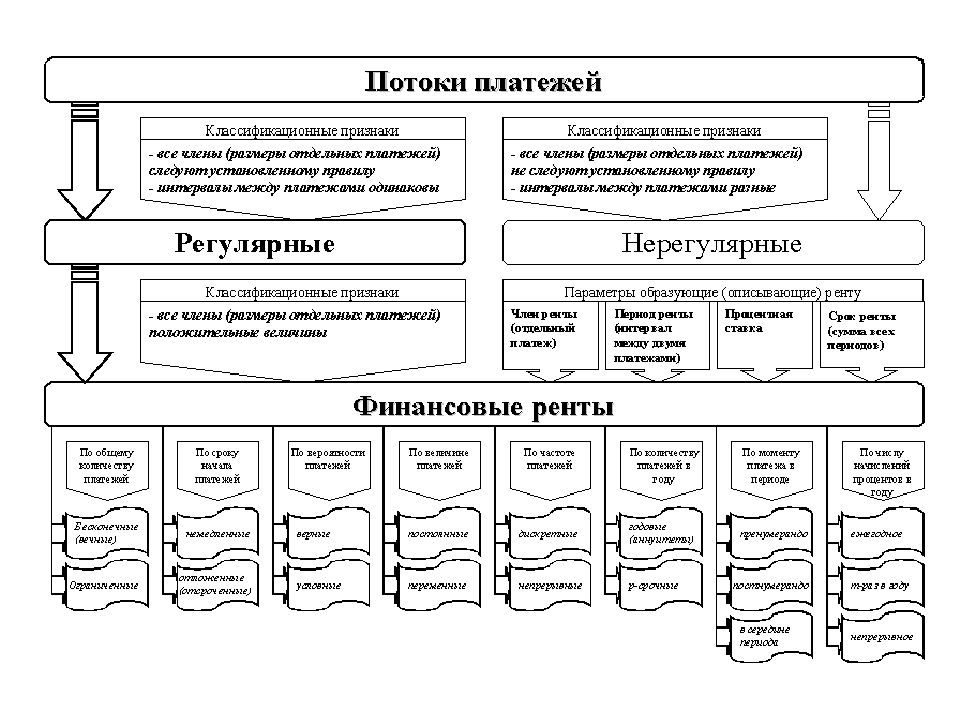
Поток платежей ( cash flow stream ) – это последовательность или ряд платежей, характеризующаяся величинами платежей (со знаками) и моментами времени, когда они осуществляются. Отдельный элемент такого ряда называется членом потока: ( cash flow ) CF 0, CF 1, …, CF n. Если значение члена потока CF n > 0 ‑ это поступления, CF n < 0 – выплаты. Потоки платежей бывают: регулярные – размеры платежей постоянные или следуют установленному правилу через равные интервалы между платежами и нерегулярные. Поток бывает конечным или бесконечным в зависимости от количества платежей в нем.
Одним из ключевых понятий в финансовых и коммерческих расчетах — понятие аннуитета. Аннуитет ( annuity ) представляет собой частный случай денежного потока, а именно, это однонаправленный поток (предполагаются либо только притоки, либо только оттоки денежных средств), в котором длительность периодов равны между собой. CF 1 = CF 2 =... = CF n = А.
Аннуитет еще называют финансовой рентой или просто рентой. Рентой является получение процентов по облигации, платежи по потребительскому кредиту, выплаты в рассрочку страховых премий и т.д. Любое денежное поступление называется членом аннуитета ( членом ренты ), а величина постоянного временного интервала между двумя последовательными денежными поступлениями называется периодом аннуитета ( периодом ренты ). Интервал времени от начала первого периода аннуитета до конца последнего называется сроком аннуитета. Очень важным является различие по моменту выплат платежей в пределах периода аннуитета. Если платежи осуществляются в конце этих периодов, то соответствующий аннуитет называется постнумерандо, если платежи производятся в начале периодов, то аннуитет называют пренумерандо (см. рис. 2.1.1). Декурсивное начисление процентов - начисление процентов в конце каждого периода. Обычно для долгосрочных ссуд используется декурсивное начисление процентов.
0 1 2 3 4 С 1 С 2 С 3 С 4 С 1 С 2 С 3 С 4 0 1 2 3 4 Рис. 2.1.1. Графическое представление потоков пренумерандо и постнумерандо Аннуитет называется постоянным, если все денежные поступления равны между собой. CF 1 = CF 2 =... = CF n = А. Если денежные поступления варьируются, то аннуитет называют переменным. Если число периодов ограничено, аннуитет называется срочным. Если в течение каждого базового периода начисления процентов денежные поступления происходят р раз, то аннуитет часто называют р-срочным. Часто в качестве такого базового периода выступает календарный год. Аннуитет называется отсроченным, если начало его первого периода сдвинуто вправо по временной оси от момента времени, на который происходит анализ. Аннуитет называется бессрочным (или вечной рентой), если число его элементов неограниченно большое (в том числе достаточно большое). В западной практике к бессрочным относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет также называют и вечной рентой.
Оценка денежного потока может выполняться в рамках решения двух задач: прямой, предполагающей суммарную оценку наращенного денежного потока ; обратной, предполагающей суммарную оценку дисконтированного денежного (приведенного) потока. Часто возникает необходимость определения и ряда других параметров финансовых операций, важнейшими из которых являются: Cf t – величина потока платежей в периоде t; r – процентная ставка; n – срок (количество периодов) проведения операции. Наращенная сумма – сумма всех членов потока платежей с начисленными на них к концу срока процентами. Под современной стоимостью потока платежей понимают сумму всех его членов, дисконтированных на начало срока аннуитета или некоторый упреждающий момент времени. 2.2. Оценка аннуитета
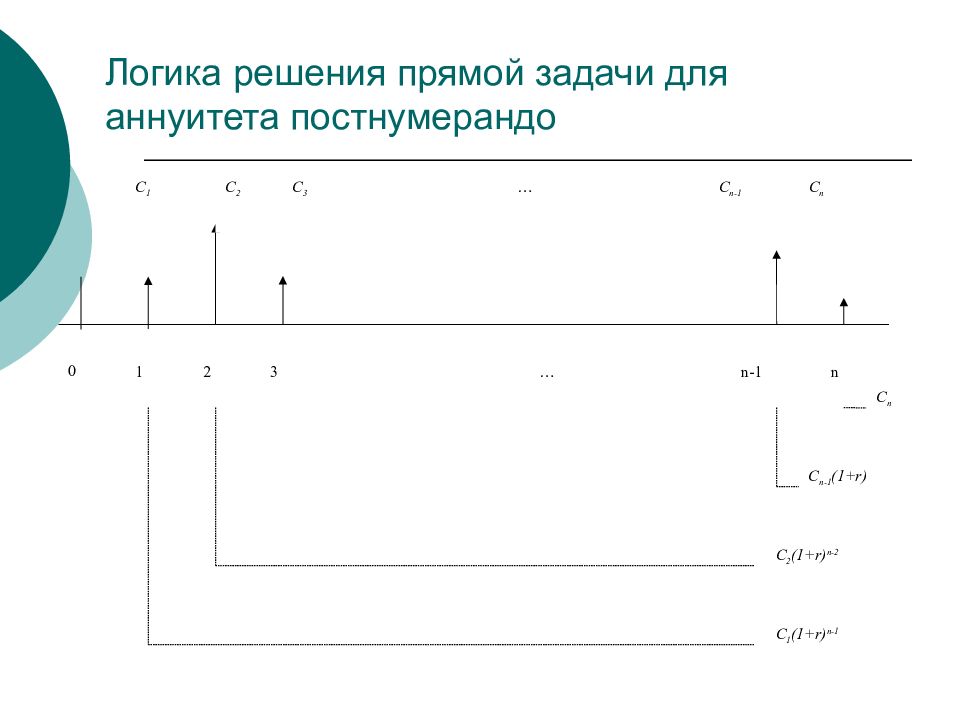
Пусть C 1, C 2, …., C n – аннуитет, период которого совпадает с базовым периодом начисления процентов по ставке r. Требуется найти стоимость данного аннуитета с позиции будущего и настоящего момента времени. Прямая задача предполагает оценку с позиции будущего, т.е. на конец периода n, когда реализуется схема наращения, которую для аннуитета постнумерандо можно представить следующим образом:
0 С 1 С 2 С 3 С n С n-1 1 2 3 n n-1 … … C n C n-1 (1+r) C 2 (1+r) n-2 C 1 (1+r) n-1 Рис. 2.2.1. Логика решения прямой задачи для аннуитета постнумерандо
Таким образом, на первое денежное поступление С 1 начисляются сложные проценты за ( n -1) период и оно в конце n -го периода станет равным С 1 (1+ r ) n -1. На второе денежное поступление С 2 начисляются сложные проценты за ( n -2) периода и оно станет равным С 2 (1+ r ) n -2 и т.д. На предпоследнее денежное поступление С n -1 проценты начисляются за один период и оно будет в конце периода равно С n -1 (1+ r ). На С n проценты не начисляются. Денежный поток переменного аннуитета постнумерандо составит: (2.2.1)
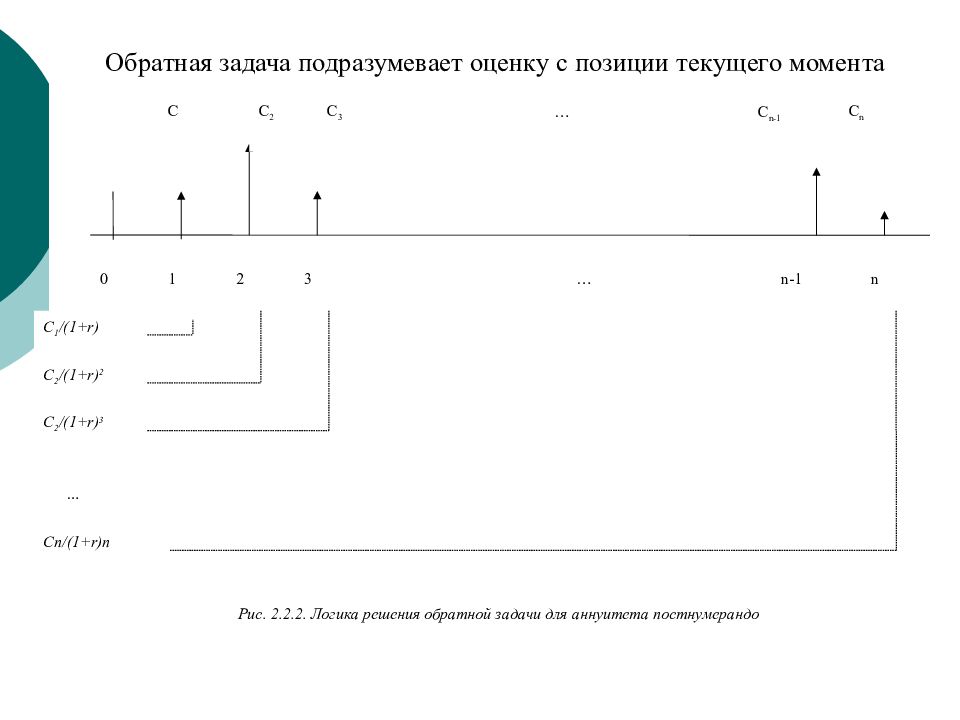
Обратная задача подразумевает оценку с позиции текущего момента С 2 /(1+ r ) 2 С 1 /(1+ r ) С 2 /(1+ r ) 3 С n /(1+ r ) n … 0 С С 2 С 3 С n С n-1 1 2 3 n n-1 … … Рис. 2.2.2. Логика решения обратной задачи для аннуитета постнумерандо
Приведенная стоимость денежного потока аннуитета постнумерандо рассчитывается по формуле: (2.2.3)
Пример 2.2.1. Клиент в конце каждого года вкладывает 3 тыс. руб. в банк, выплачивающий сложные проценты по процентной ставке 25% годовых. Определите сумму, которая будет на счете клиента через 7 лет. Если эта сумма получается в результате однократного помещения денег в банк в начале первого года, то какой величины должен быть взнос? Решение. Первый вариант помещения денег является постоянным аннуитетом постнумерандо, член которого равен 3 тыс. руб., срок - 7 лет, и период равен одному году. Изобразим схематично эту ситуацию на оси времени (одно деление равно одному году), помещая над осью члены аннуитета.
Для определения суммы на счете через 7 лет (т.е. будущей стоимости аннуитета) можно воспользоваться общей формулой (2.1.1), полагая r =0,25, С 1 =С2,.. = С7 =3. тыс. руб. Значение коэффициента наращения аннуитета F МЗ(25%,1) можно либо взять из таблиц, либо вычислить непосредственно по формуле, определяющей этот коэффициент. Для определения величины взноса (в начале первого года), который при наращении сложными процентами через 7 лет станет равным 45,221 тыс. руб., можно воспользоваться формулой нахождения приведенной стоимости аннуитета. Применяя формулу, находим: тыс. руб.
Определим наращенный поток переменного аннуитета пренумерандо : или . ( 2.2.5) (2.2.6)
Рассмотрим случай постоянного срочного аннуитета постнумерандо. Пусть в течение n лет в банк в конце каждого года вносится по A руб. На взносы начисляются сложные проценты, по r процентов годовых. Таким образом, все члены ренты, кроме последнего, приносят проценты – на первый член проценты начисляются n-1 год, на второй n-2 и т.д. Наращенная к концу срока сумма составит: Перепишем этот же ряд в обратном порядке: Этот ряд представляет собой геометрическую прогрессию * со знаменателем ( 1+ r ) и первым членом A, число членов n. где ‑ коэффициент наращения аннуитета, представляет собой наращенную сумму ренты, член которой равен 1. Он зависит только от срока и процентной ставки. Значения коэффициента наращения аннуитета табулированы для различных значений процентной ставки и сроков действия аннуитета. * Напомним формула суммы n –первых членов геометрической прогрессии Оценка постоянного аннуитета постнумерандо
Пример 2.2.1. На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета. Решение. Поскольку период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента. Сумма всех взносов с начисленными процентами будет равна: Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами, содержащими коэффициенты наращения ренты: Сумма взносов в течение 5 лет составит: S = 5 • 500 = 2500 руб. Следовательно, сумма начисленных процентов будет равна: I = FV - S = 4521,55 - 2500 = 2021,55 руб. Таким образом, доход владельца счета за 5 лет составит 2021,55 руб. Приведенная стоимость постоянного аннуитета постнумерандо PVapst может быть рассчитана следующим образом:
(2.2.8) Множитель называется коэффициентом дисконтирования ренты (аннуитета) и как сумма членов геометрической прогрессии равен величине Приведенная стоимость постоянного аннуитета постнумерандо PV a pst может быть рассчитана следующим образом:
Рассмотрим нахождение величин наращенной суммы и приведенной стоимости срочного постоянного аннуитета пренумерандо. Наращенный денежный поток имеет вид: (2.2.9) (2.2.10) Оценка постоянного аннуитета пренумерандо
Если r – процентная ставка (в десятичных дробях) за базовый период, а начисление сложных процентов происходит m раз в течение этого периода, то наращенный поток, начиная с последнего денежного поступления имеет вид: Получили геометрическую прогрессию, первый член которой равен A и знаменатель – Следовательно, сумма n первых членов этой прогрессии равна: (2.2.11)
Рассмотрим ситуацию, когда в течение базового периода начисления процентов денежные поступления происходят несколько раз, а проценты начисляются один раз в конце периода. Пусть в течение базового периода денежные поступления происходят p раз и один раз в конце периода начисляются проценты в соответствии со ставкой r. На последнее p -е поступление проценты не начисляются и оно остается A. На предпоследнее ( p -1 )-е поступление начисляются сложные проценты за 1/p -ю часть периода и оно будет равно A(1+ r ) 1/ p. На ( p -2 )-е поступление начисляются сложные проценты за 2 /p -ю часть периода и оно будет равно A(1+ r ) 2/ p и.т. д. до первого включительно, которое будет равно A(1+ r ) p -1/ p. Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом A, знаменателем (1+ r ) 1/ p и числом членов, равным p, поэтому сумма этих величин равна:
Таким образом, имеем аннуитет, в котором денежные поступления равны величине и происходят в конце каждого базового периода начисления процентов. Пользуясь формулой 2.1.7, получим (2.2.12) т.к или (2.2.13) Самостоятельно выведите формулы приведенной стоимости переменного и постоянного аннуитета пренумерандо, проиллюстрировать графически.
В финансовых операциях возможны ситуации, когда величина платежа либо увеличивается, либо уменьшается с течением времени, например, под влиянием инфляции. В таких случаях говорят о нерегулярных потоках платежей. Нерегулярные потоки платежей характеризуются присутствием хотя бы одного нерегулярного параметра: период ренты или размер платежа. Для получения их обобщающих характеристик требуется прямой счет, т.е. вычисление соответствующих характеристик по каждому платежу и последующему их суммированию.
Поток 1 2 3 4 5 А 100 200 200 300 300 В 200 - 200 - 200 Решение: Для решения данной задачи произведем прямой расчет наращенной суммы по каждому периоду, представив данные в виде таблиц. Таким образом, наращенная сумма потока А через пять лет составит 1'325,21 рублей. Для потока В наращенная сумма через пять лет составит 765,59 рублей.
Дайте определение потока платежей. Что понимают под термином аннуитет? Какие виды аннуитетов Вы знаете? Оценка переменного аннуитета постнумерандо и пренумерандо. Оценка постоянного аннуитета постнумерандо и пренумерандо. Оценка постоянного p -срочного аннуитета постнумерандо и пренумерандо. Анализ инвестиционных проектов в условиях инфляции
