Скачать
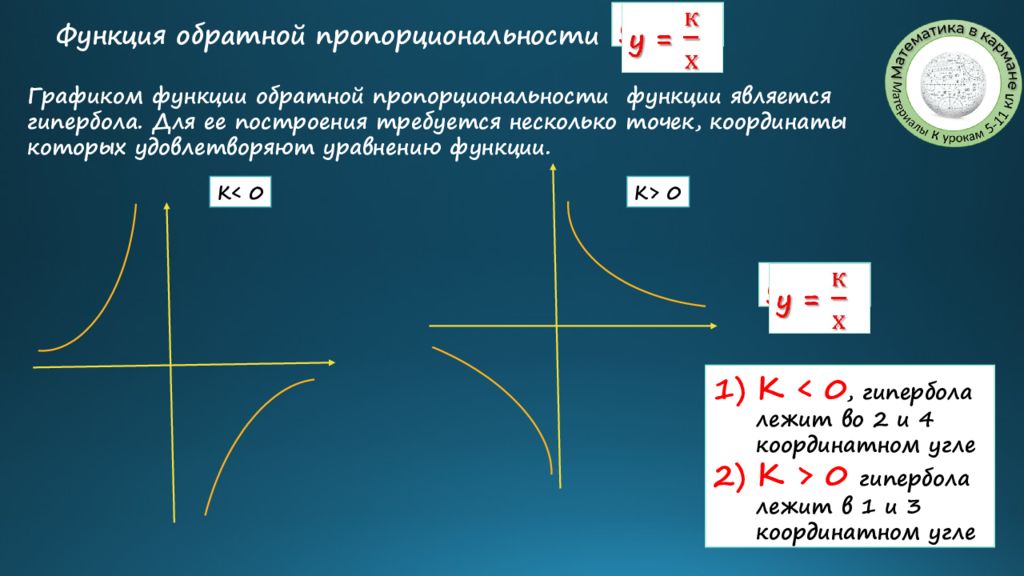
Графиком функции обратной пропорциональности функции является гипербола. Для ее построения требуется несколько точек, координаты которых удовлетворяют уравнению функции. Функция обратной пропорциональности y = К < 0, гипербола лежит во 2 и 4 координатном угле К > 0 гипербола лежит в 1 и 3 координатном угле K> 0 K< 0 y =
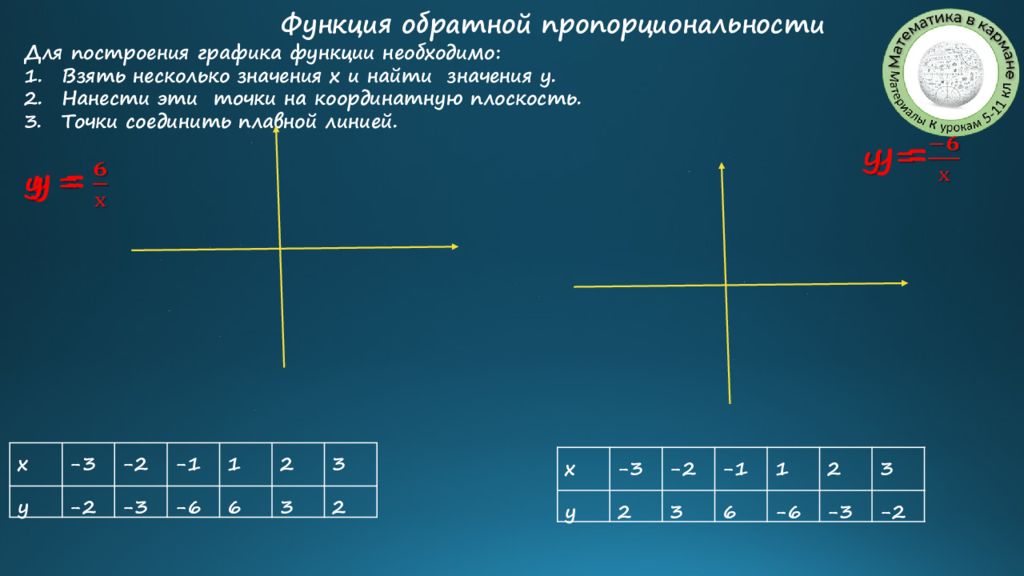
Для построения графика функции необходимо: Взять несколько значения х и найти значения у. Нанести эти точки на координатную плоскость. Точки соединить плавной линией. Функция обратной пропорциональности у = х -3 -2 -1 1 2 3 у -2 -3 -6 6 3 2 у = х -3 -2 -1 1 2 3 у 2 3 6 -6 -3 -2
Графиком функции арифметического квадратного корня является ветвь гиперболы. Для ее построения необходимо несколько точек, координаты которых удовлетворяют уравнению функции. Функция арифметического квадратного корня Функция модуля
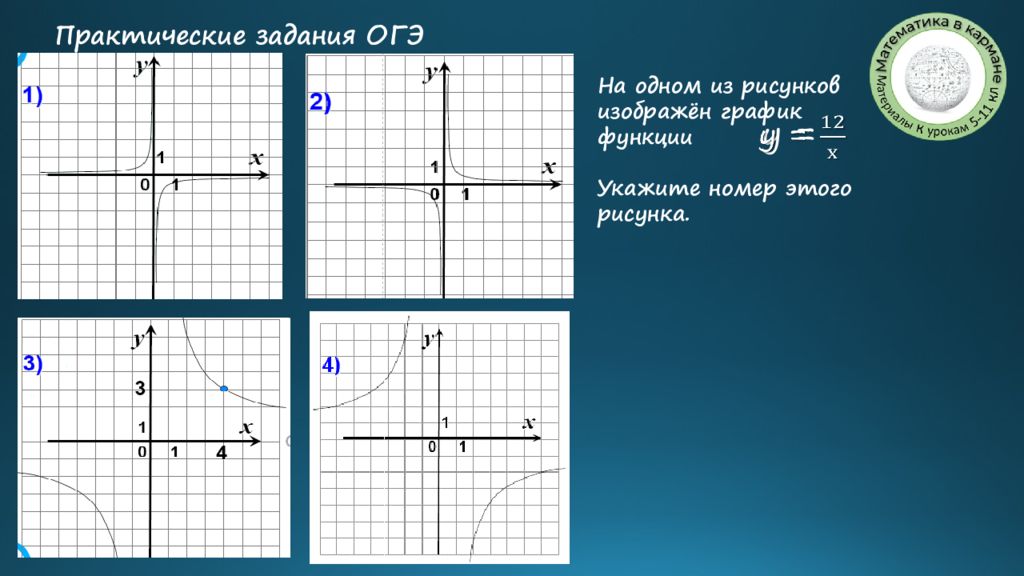
На одном из рисунков изображён график функции Укажите номер этого рисунка. Практические задания ОГЭ у =
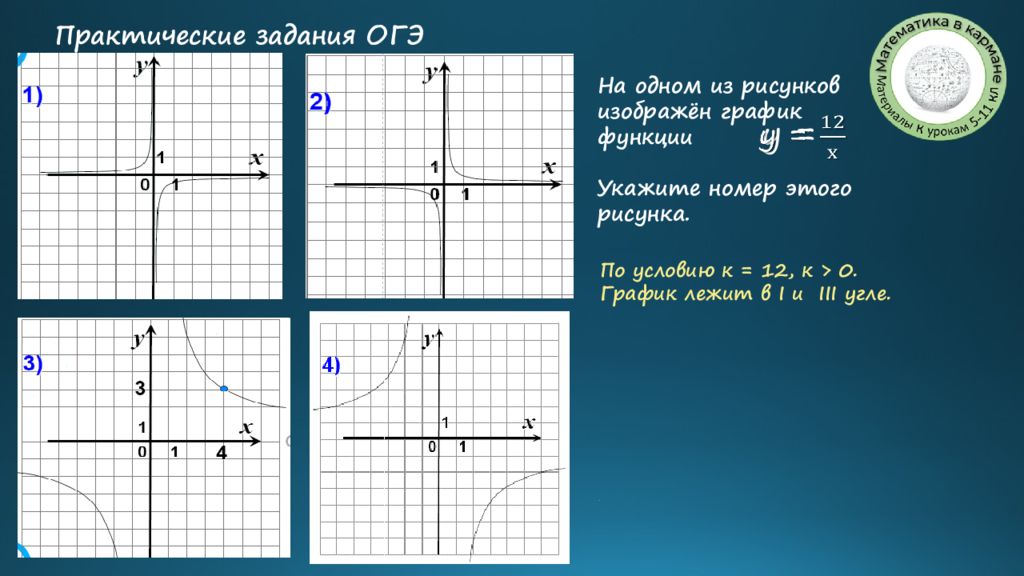
На одном из рисунков изображён график функции Укажите номер этого рисунка. Практические задания ОГЭ у = По условию к = 12, к > 0. График лежит в I и III угле.
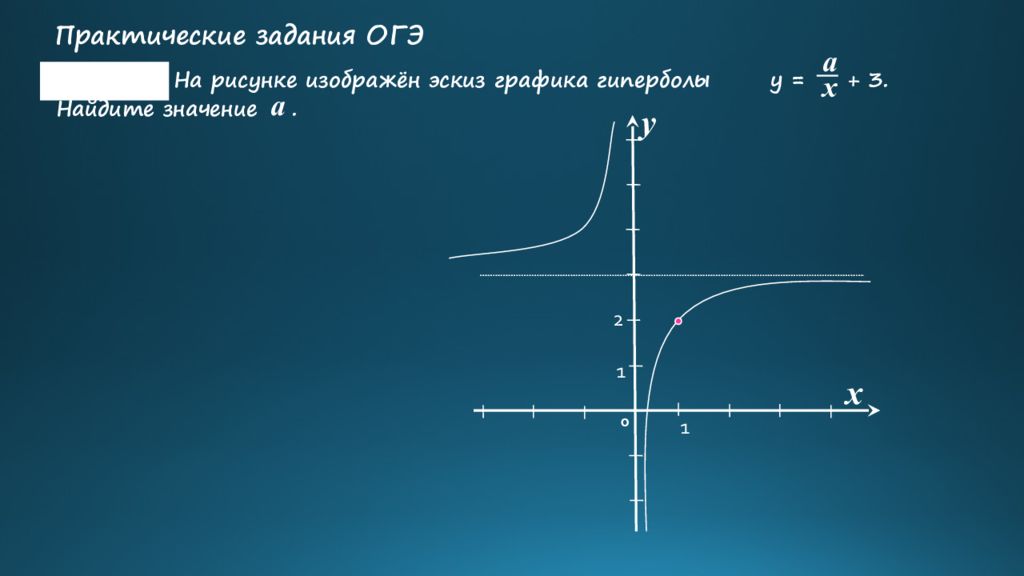
x y 0 1 2 1 x a На рисунке изображён эскиз графика гиперболы y = + 3. Найдите значение. a Задание: Практические задания ОГЭ
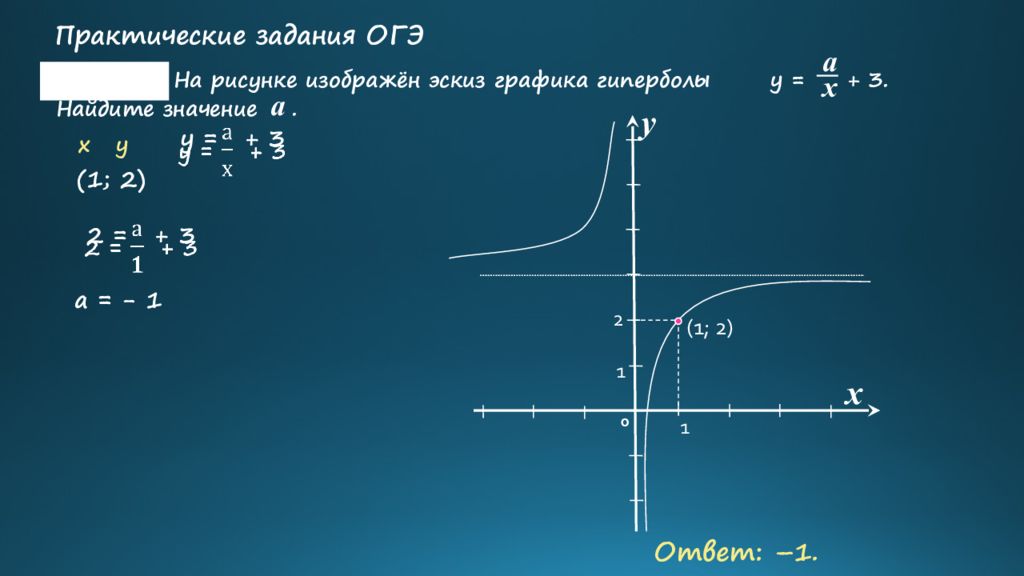
x y 0 (1; 2 ) Ответ: –1. 1 2 1 (1; 2 ) x y x a y = + 3 На рисунке изображён эскиз графика гиперболы y = + 3. Найдите значение. a Задание: Практические задания ОГЭ 2 = + 3 а = - 1
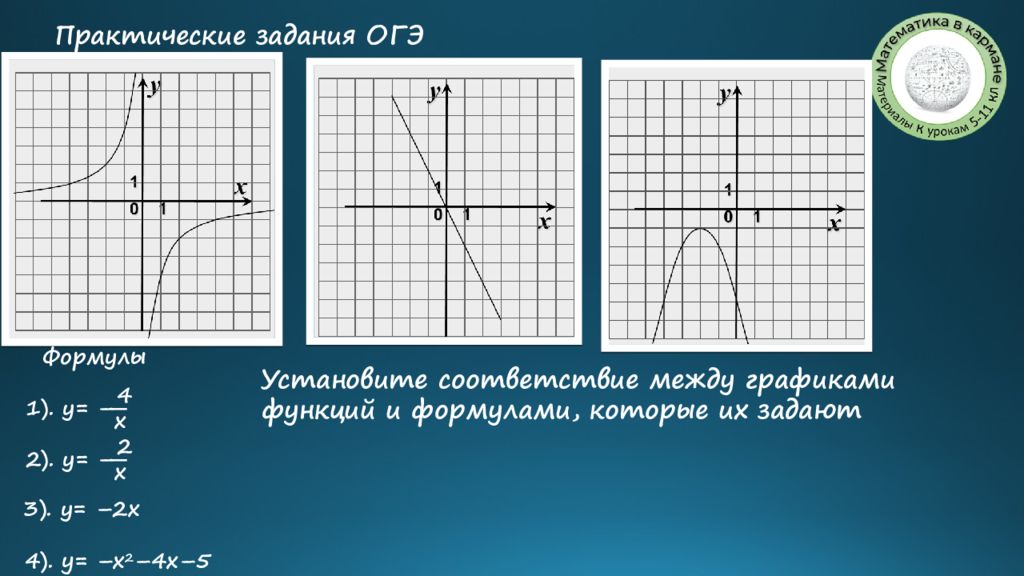
Установите соответствие между графиками функций и формулами, которые их задают Практические задания ОГЭ Формулы 3 ). у= –2x 4 x 1 ). у= – 4 ). y= –x 2 –4x–5 2 x 2 ). у= –
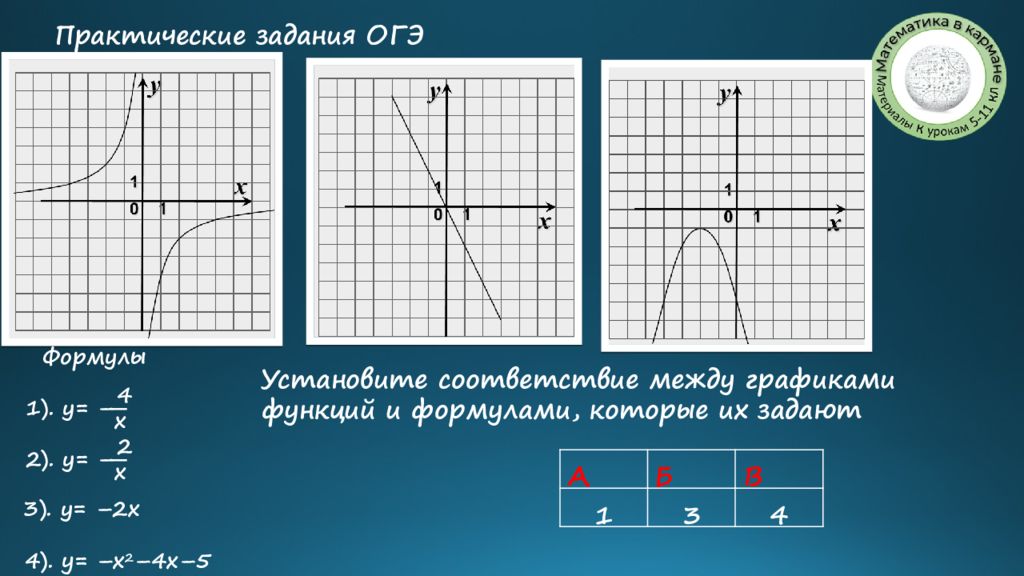
Установите соответствие между графиками функций и формулами, которые их задают Практические задания ОГЭ Формулы 3 ). у= –2x 4 x 1 ). у= – 4 ). y= –x 2 –4x–5 2 x 2 ). у= – А Б В 1 3 4
На рисунке изображен график функции y=f(x). Укажите решение неравенства f(x) – 2. 1). [ – 2; 6], 2). x = 2, 3) [ – 2; 1 ], 4). [ 1 ; 6]. 0 1 x y 1 2 Практические задания ОГЭ
Ответ: 2. На рисунке изображен график функции y=f(x). Укажите решение неравенства f(x) – 2. 1). [ – 2; 6], 2). x = 2, 3) [ – 2; 1 ], 4). [ 1 ; 6]. 0 1 x y 1 f(x ) = –2 f(x ) < –2 y = –2 2 Практические задания ОГЭ
