Слайд 2
Часто наборы данных представляют собой обширные массивы. Среди них встречаются очень близкие друг к другу значения, но полное совпадение встречается крайне редко, даже если данных очень много. Чтобы понять, насколько плотно распределены значения на каждом участке числовой прямой, применяют группировку данных. Чтобы сгруппировать данные, нужно разбить числовую прямую на одинаковые промежутки – интервалы группировки. Длина интервала называется шагом группировки. Затем нужно подсчитать, сколько значений или какая доля значений попала в каждый интервал, и построить диаграмму. По внешнему виду диаграммы часто можно увидеть, где именно находится среднее значение, медиана, заметить другие особенности распределения данных.
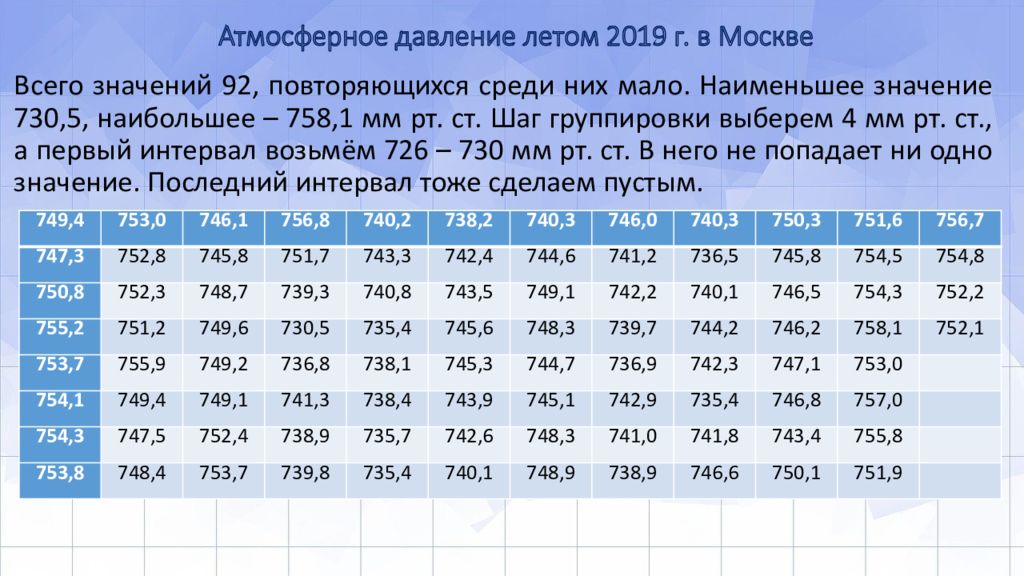
Слайд 3: Атмосферное давление летом 2019 г. в Москве
Всего значений 92, повторяющихся среди них мало. Наименьшее значение 730,5, наибольшее – 758,1 мм рт. ст. Шаг группировки выберем 4 мм рт. ст., а первый интервал возьмём 726 – 730 мм рт. ст. В него не попадает ни одно значение. Последний интервал тоже сделаем пустым. 749,4 753,0 746,1 756,8 740,2 738,2 740,3 746,0 740,3 750,3 751,6 756,7 747,3 752,8 745,8 751,7 743,3 742,4 744,6 741,2 736,5 745,8 754,5 754,8 750,8 752,3 748,7 739,3 740,8 743,5 749,1 742,2 740,1 746,5 754,3 752,2 755,2 751,2 749,6 730,5 735,4 745,6 748,3 739,7 744,2 746,2 758,1 752,1 753,7 755,9 749,2 736,8 738,1 745,3 744,7 736,9 742,3 747,1 753,0 754,1 749,4 749,1 741,3 738,4 743,9 745,1 742,9 735,4 746,8 757,0 754,3 747,5 752,4 738,9 735,7 742,6 748,3 741,0 741,8 743,4 755,8 753,8 748,4 753,7 739,8 735,4 740,1 748,9 738,9 746,6 750,1 751,9
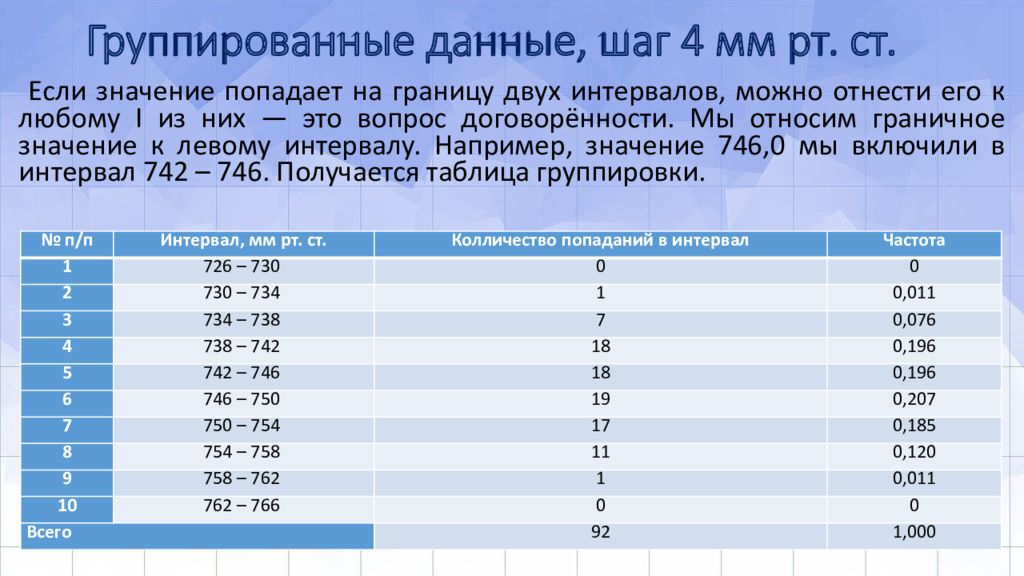
Слайд 4: Группированные данные, шаг 4 мм рт. ст
Если значение попадает на границу двух интервалов, можно отнести его к любому I из них — это вопрос договорённости. Мы относим граничное значение к левому интервалу. Например, значение 746,0 мы включили в интервал 742 – 746. Получается таблица группировки. № п/п Интервал, мм рт. ст. Колличество попаданий в интервал Частота 1 726 – 730 0 0 2 730 – 734 1 0,011 3 734 – 738 7 0,076 4 738 – 742 18 0,196 5 742 – 746 18 0,196 6 746 – 750 19 0,207 7 750 – 754 17 0,185 8 754 – 758 11 0,120 9 758 – 762 1 0,011 10 762 – 766 0 0 Всего 92 1,000
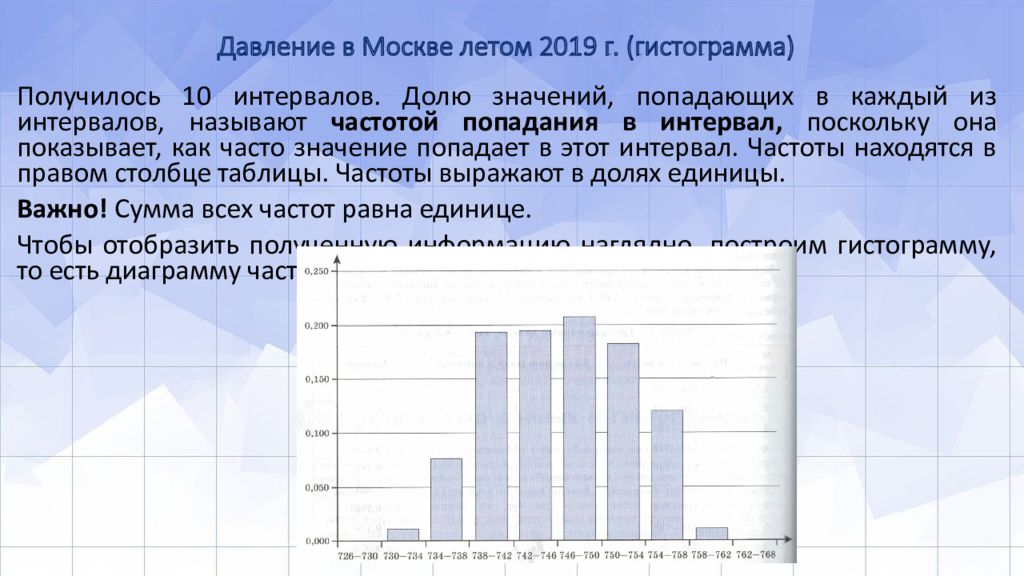
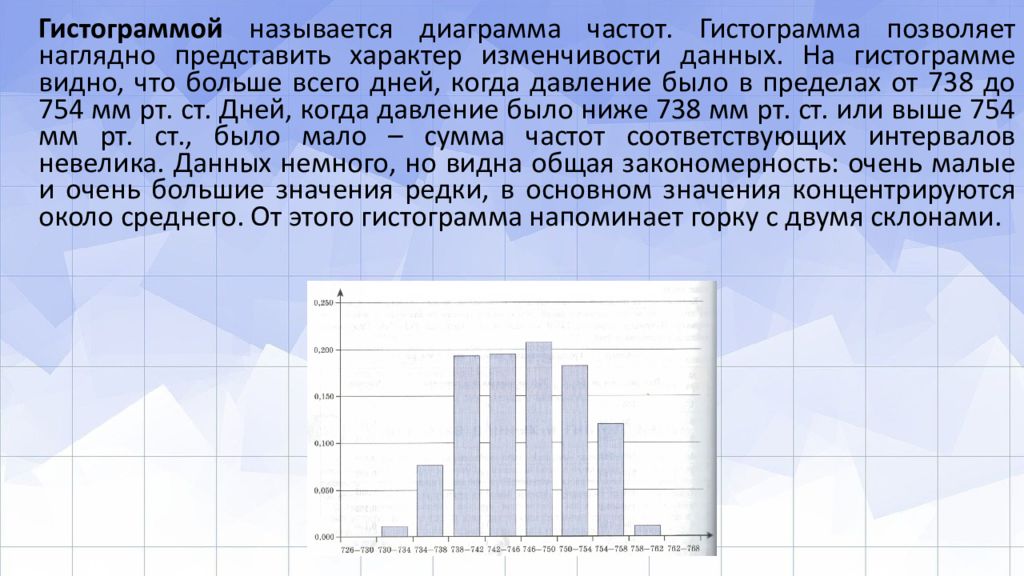
Слайд 5: Давление в Москве летом 2019 г. (гистограмма)
Получилось 10 интервалов. Долю значений, попадающих в каждый из интервалов, называют частотой попадания в интервал, поскольку она показывает, как часто значение попадает в этот интервал. Частоты находятся в правом столбце таблицы. Частоты выражают в долях единицы. Важно! Сумма всех частот равна единице. Чтобы отобразить полученную информацию наглядно, построим гистограмму, то есть диаграмму частот
Слайд 6
Гистограммой называется диаграмма частот. Гистограмма позволяет наглядно представить характер изменчивости данных. На гистограмме видно, что больше всего дней, когда давление было в пределах от 738 до 754 мм рт. ст. Дней, когда давление было ниже 738 мм рт. ст. или выше 754 мм рт. ст., было мало – сумма частот соответствующих интервалов невелика. Данных немного, но видна общая закономерность: очень малые и очень большие значения редки, в основном значения концентрируются около среднего. От этого гистограмма напоминает горку с двумя склонами.
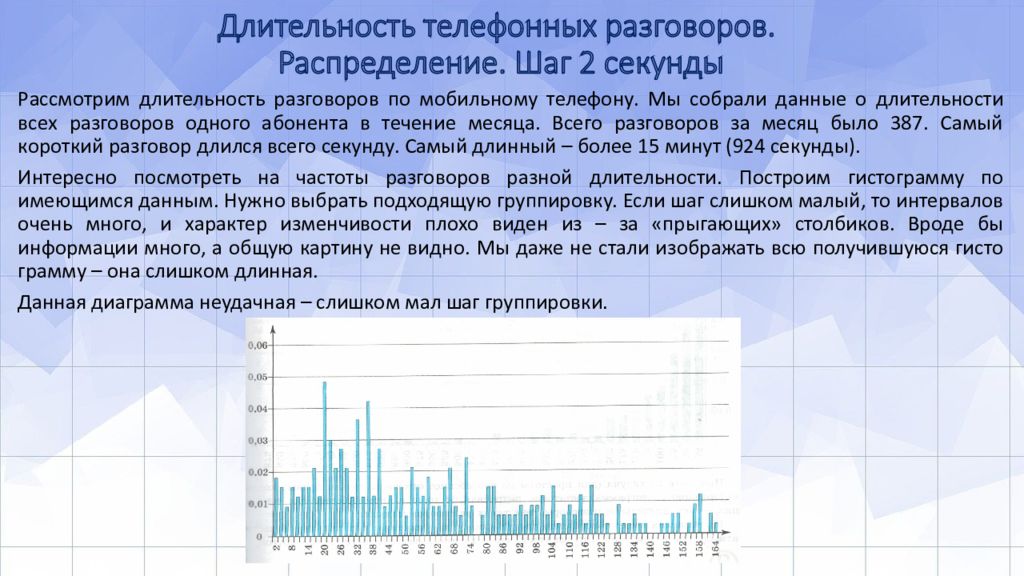
Слайд 7: Длительность телефонных разговоров. Распределение. Шаг 2 секунды
Рассмотрим длительность разговоров по мобильному телефону. Мы собрали данные о длительности всех разговоров одного абонента в течение месяца. Всего разговоров за месяц было 387. Самый короткий разговор длился всего секунду. Самый длинный – более 15 минут (924 секунды). Интересно посмотреть на частоты разговоров разной длительности. Построим гистограмму по имеющимся данным. Нужно выбрать подходящую группировку. Если шаг слишком малый, то интервалов очень много, и характер изменчивости плохо виден из – за «прыгающих» столбиков. Вроде бы информации много, а общую картину не видно. Мы даже не стали изображать всю получившуюся гистограмму – она слишком длинная. Данная диаграмма неудачная – слишком мал шаг группировки.
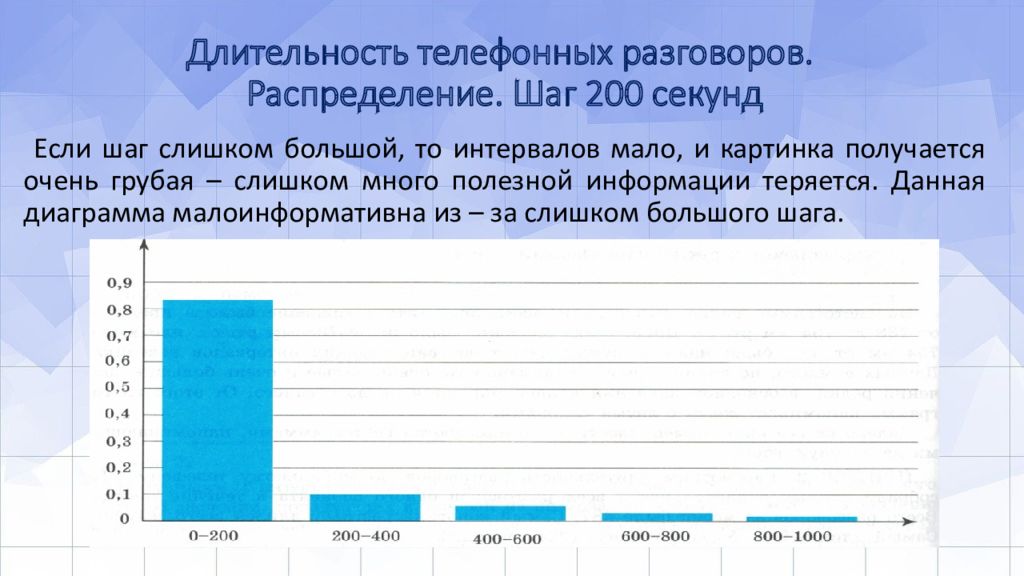
Слайд 8: Длительность телефонных разговоров. Распределение. Шаг 200 секунд
Если шаг слишком большой, то интервалов мало, и картинка получается очень грубая – слишком много полезной информации теряется. Данная диаграмма малоинформативна из – за слишком большого шага.
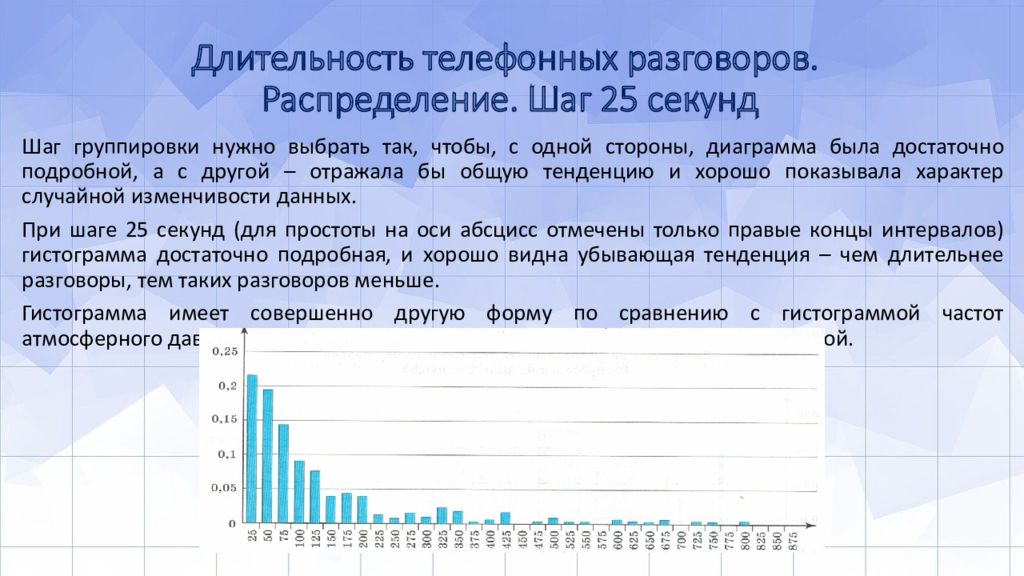
Слайд 9: Длительность телефонных разговоров. Распределение. Шаг 25 секунд
Шаг группировки нужно выбрать так, чтобы, с одной стороны, диаграмма была достаточно подробной, а с другой – отражала бы общую тенденцию и хорошо показывала характер случайной изменчивости данных. При шаге 25 секунд (для простоты на оси абсцисс отмечены только правые концы интервалов) гистограмма достаточно подробная, и хорошо видна убывающая тенденция – чем длительнее разговоры, тем таких разговоров меньше. Гистограмма имеет совершенно другую форму по сравнению с гистограммой частот атмосферного давления. Это означает, что и характер изменчивости совсем другой.
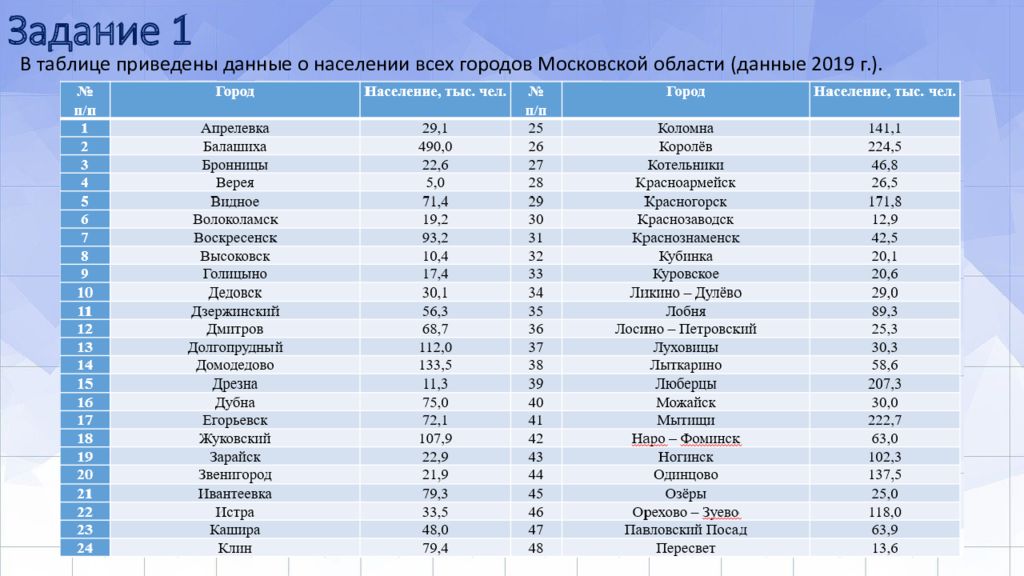
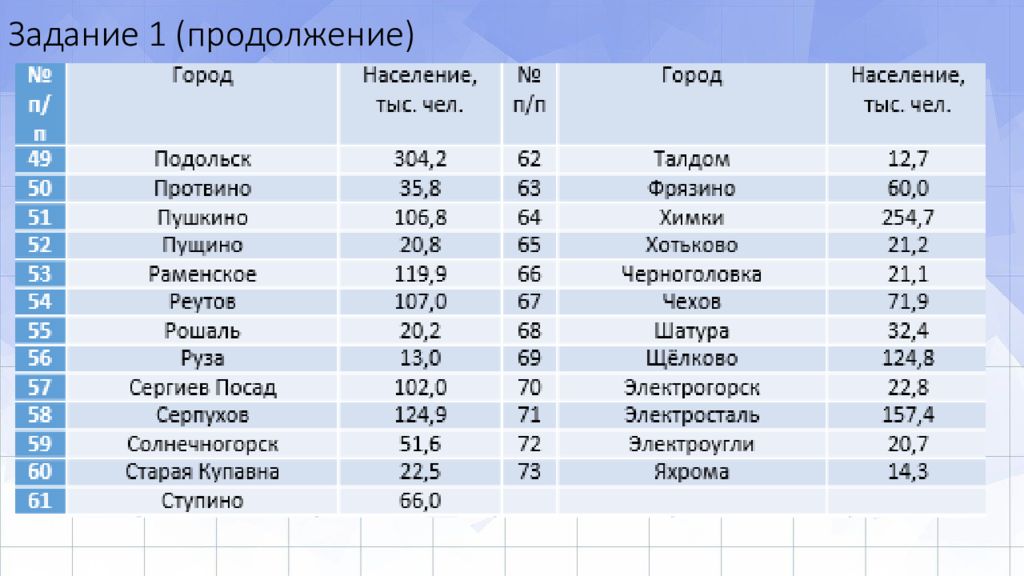
Слайд 11: Задание 1
В таблице приведены данные о населении всех городов Московской области (данные 2019 г.).
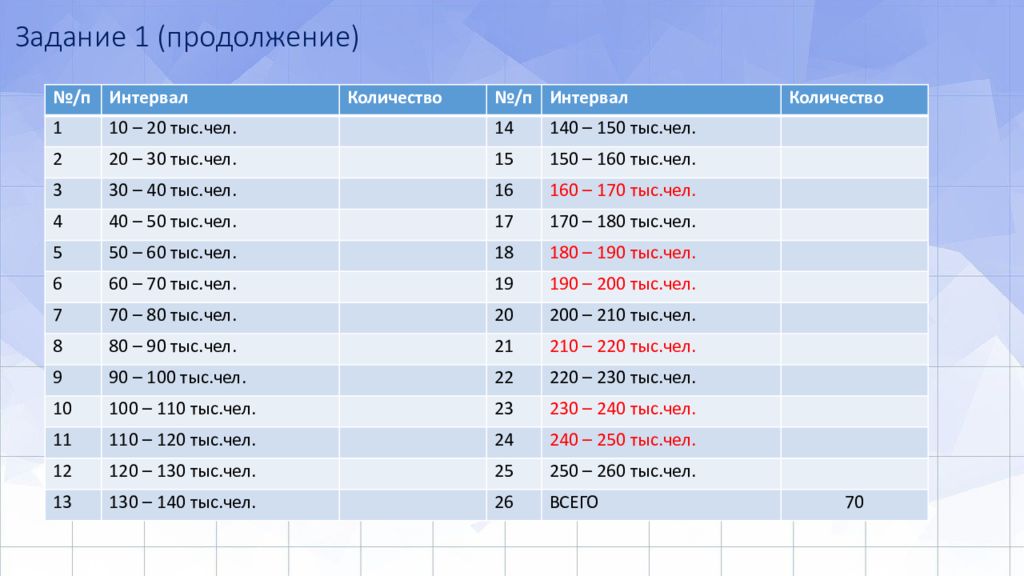
Слайд 13: Задание 1 (продолжение)
№/п Интервал Количество №/п Интервал Количество 1 10 – 20 тыс.чел. 14 140 – 150 тыс.чел. 2 20 – 30 тыс.чел. 15 150 – 160 тыс.чел. 3 30 – 40 тыс.чел. 16 160 – 170 тыс.чел. 4 40 – 50 тыс.чел. 17 170 – 180 тыс.чел. 5 50 – 60 тыс.чел. 18 180 – 190 тыс.чел. 6 60 – 70 тыс.чел. 19 190 – 200 тыс.чел. 7 70 – 80 тыс.чел. 20 200 – 210 тыс.чел. 8 80 – 90 тыс.чел. 21 210 – 220 тыс.чел. 9 90 – 100 тыс.чел. 22 220 – 230 тыс.чел. 10 100 – 110 тыс.чел. 23 230 – 240 тыс.чел. 11 110 – 120 тыс.чел. 24 240 – 250 тыс.чел. 12 120 – 130 тыс.чел. 25 250 – 260 тыс.чел. 13 130 – 140 тыс.чел. 26 ВСЕГО 70
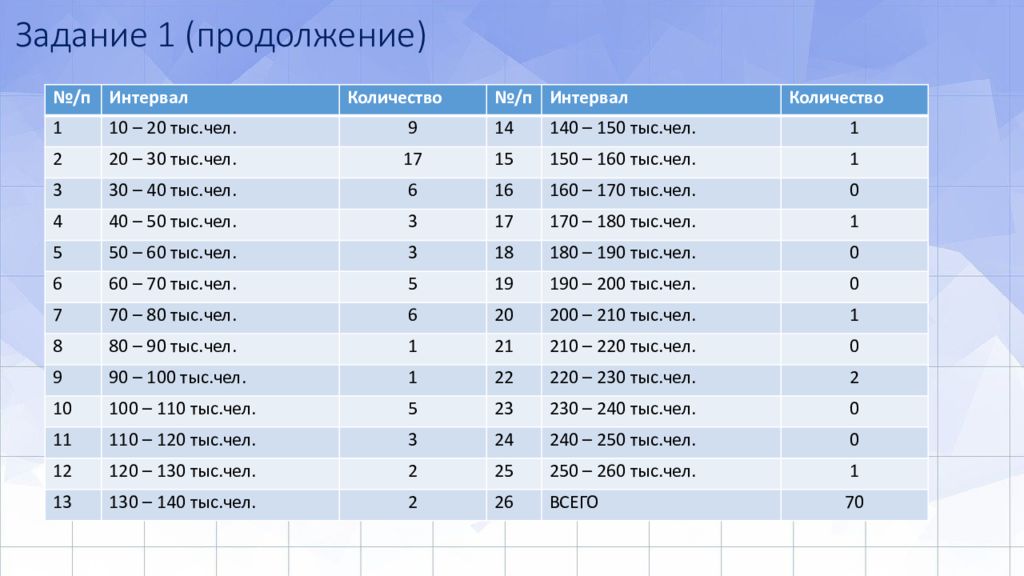
Слайд 14: Задание 1 (продолжение)
№/п Интервал Количество №/п Интервал Количество 1 10 – 20 тыс.чел. 9 14 140 – 150 тыс.чел. 1 2 20 – 30 тыс.чел. 17 15 150 – 160 тыс.чел. 1 3 30 – 40 тыс.чел. 6 16 160 – 170 тыс.чел. 0 4 40 – 50 тыс.чел. 3 17 170 – 180 тыс.чел. 1 5 50 – 60 тыс.чел. 3 18 180 – 190 тыс.чел. 0 6 60 – 70 тыс.чел. 5 19 190 – 200 тыс.чел. 0 7 70 – 80 тыс.чел. 6 20 200 – 210 тыс.чел. 1 8 80 – 90 тыс.чел. 1 21 210 – 220 тыс.чел. 0 9 90 – 100 тыс.чел. 1 22 220 – 230 тыс.чел. 2 10 100 – 110 тыс.чел. 5 23 230 – 240 тыс.чел. 0 11 110 – 120 тыс.чел. 3 24 240 – 250 тыс.чел. 0 12 120 – 130 тыс.чел. 2 25 250 – 260 тыс.чел. 1 13 130 – 140 тыс.чел. 2 26 ВСЕГО 70
Слайд 15: Задание 1 (продолжение)
а) Найдите три подмосковных города, где численность населения значительно отличается от численности населения большинства городов в ту или другую сторону. б) Удалите из таблицы три найденных в пункте а) города. Найдите наименьшее и наибольшее значения после удаления этих трёх городов. в) После удаления из таблицы городов Балашихи, Подольска и Вереи нужно сгруппировать оставшиеся данные. г) Сколько интервалов группировки получится, если сделать начальное значение 10 тыс. чел. при шаге группировки 10 тыс. чел.? д) Сколько городов из таблицы попадает в интервал 90 – 120 тыс. чел.? е) Какова частота попадания в интервал 90 – 120 тыс. чел.? ОТВЕТ: 25 ОТВЕТ: 9 ОТВЕТ: 0,13
Последний слайд презентации: Группировка данных и гистограммы: Домашнее задание:
Для таблицы задания № 1 выполнить: Сколько интервалов группировки получится, если сделать начальное значение 0 тыс. чел., а шаг группировки 25 тыс. чел.? Сколько городов из таблицы 78 попадает в интервал 90 – 120 тыс. чел.? Какова частота попадания в интервал 90 – 120 тыс. чел.? Какой из этих двух способов группировки вы бы предпочли? Постройте гистограмму.