Импеданс (комплексное сопротивление)
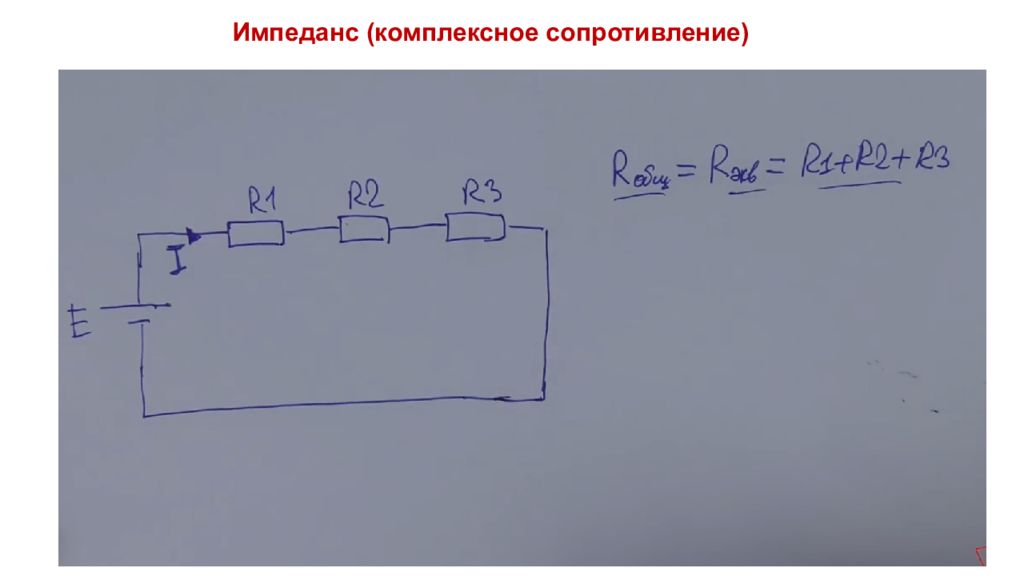
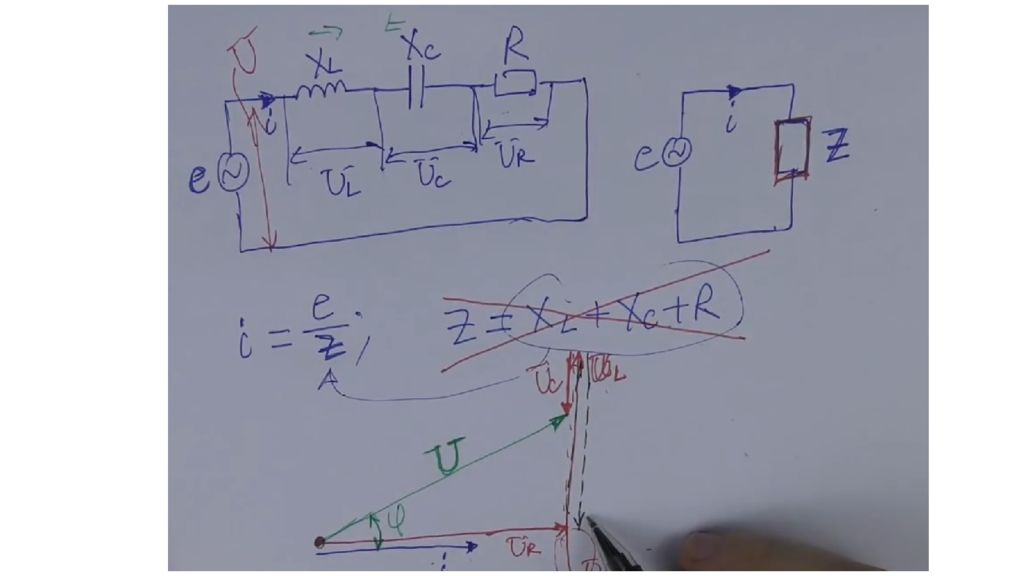
Полное сопротивление (импеданс) — комплексная величина электрической цепи, выраженная действительным сопротивлением и мнимым реактивным сопротивлением, препятствующая прохождению электрического тока. При измерении импеданса мы всегда должны питать цепь переменным током, в случае постоянного тока мы будем измерять только действительную составляющую импеданса. Значение импеданса В цепях постоянного тока активное сопротивление R играет важную роль. Что касается цепей синусоидального переменного тока, то здесь не обойтись одним лишь активным сопротивлением. Ведь если в цепях постоянного тока емкости и индуктивности заметны только при переходных процессах, то в цепях переменного тока данные компоненты проявляют себя гораздо более значительно. Поэтому для адекватного расчета цепей переменного тока вводится термин «электрический импеданс» - Z или комплексное (полное) сопротивление двухполюсника гармоническому сигналу. Иногда говорят просто «импеданс», отбрасывая слово «электрический».
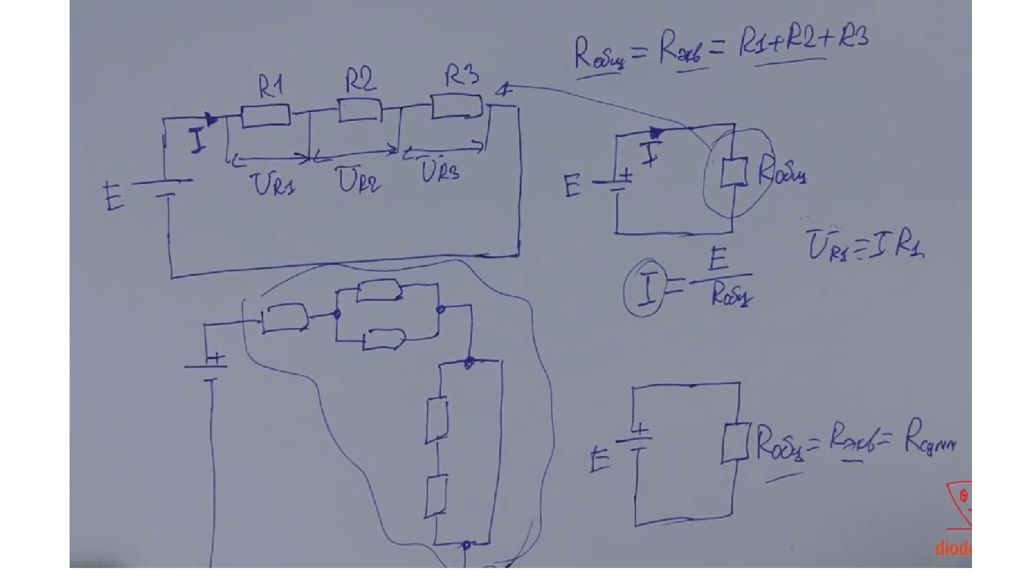
Представление об импедансе позволяет применять закон Ома к участкам цепей переменного синусоидального тока. Проявление двухполюсником (нагрузкой) индуктивной составляющей приводит к отставанию тока от напряжения на данной частоте, а проявление емкостной составляющей — к отставанию напряжения от тока. Активная же составляющая не вызывает задержки между током и напряжением, проявляя себя по сути так же, как и в цепи постоянного тока.
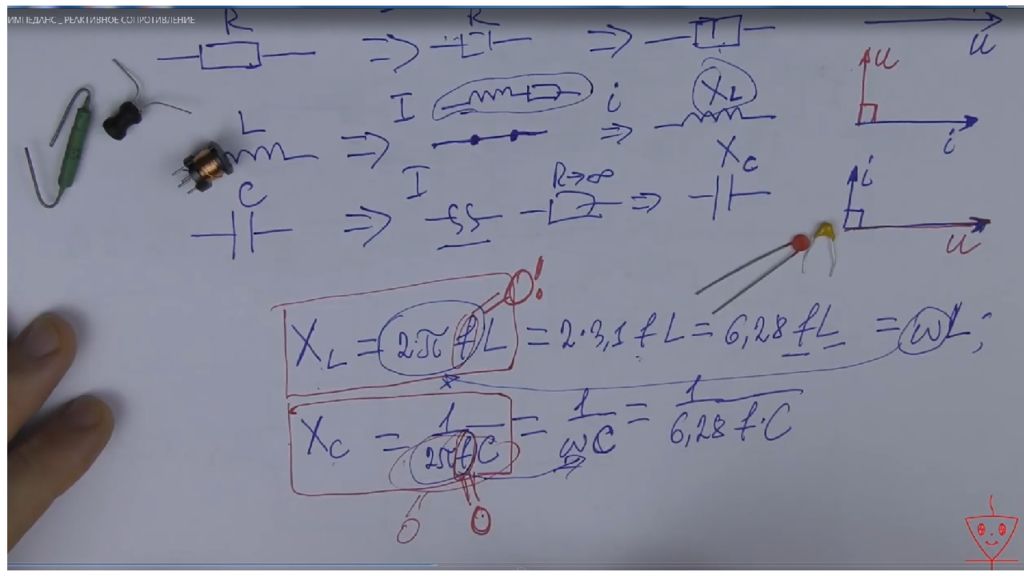
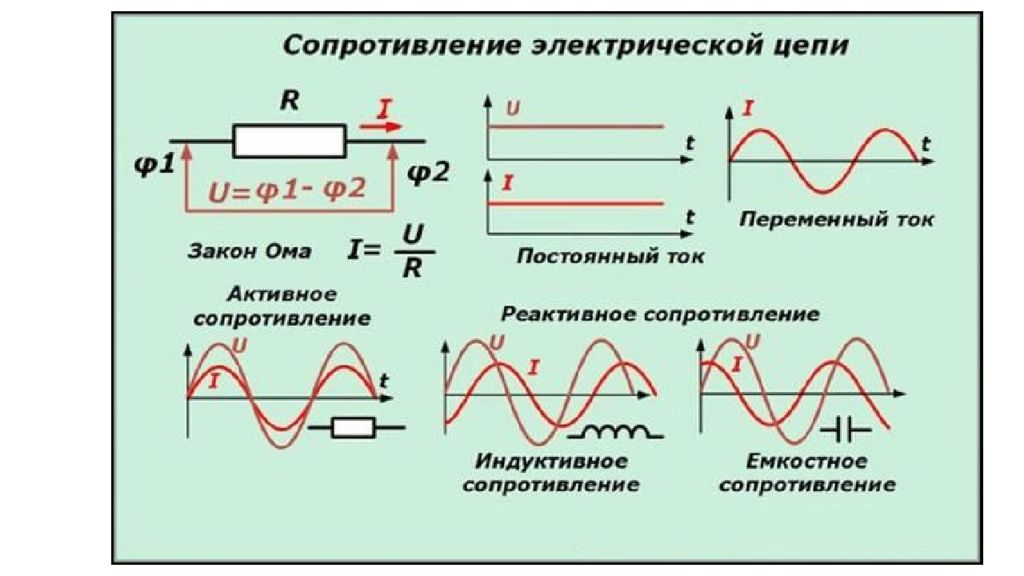
Активное сопротивление (R) является мерой интенсивности противодействия движению электронов между атомами. Чем легче атомы отдают/принимают электроны, тем ниже этот параметр, выражающийся в положительных действительных числах. Реактивное сопротивление, обозначаемое буквой Х, представляет собой выражение степени, с которой электронный компонент, схема или система накапливает или высвобождает энергию при колебаниях тока и напряжения за каждый единичный цикл переменного тока. Импедансом часто называют модуль комплексного сопротивления, поэтому реактивное сопротивление выражается в так называемых «мнимых» омах. Оно характерно только для линий переменного тока. Когда переменный электроток проходит через катушку индуктивности, накапливаемая энергия высвобождается в виде магнитного поля. В этом случае реактивная составляющая импеданса является индуктивной (обозначается + jX L ). Чем быстрее меняется направление тока, тем Х L больше. Однако энергия может запасаться и высвобождаться в виде электрического поля, тогда данный параметр будет емкостным (обозначается – jX C ). Когда ток меняет направление, конденсатор многократно заряжается и разряжается. Чем больше времени конденсатор заряжается, тем сильнее он противодействует электротоку. Поэтому чем быстрее меняется направление электротока, тем ниже емкостное сопротивление. Реактивное сопротивление обычно умножается на положительный квадратный корень из –1, который представляет собой единичное мнимое число j. Тогда комплексное сопротивление Z выражается как R + jX L или R – jX C. Следовательно, активное сопротивление R — это действительная часть комплексного импеданса, а реактивное Х — мнимая.
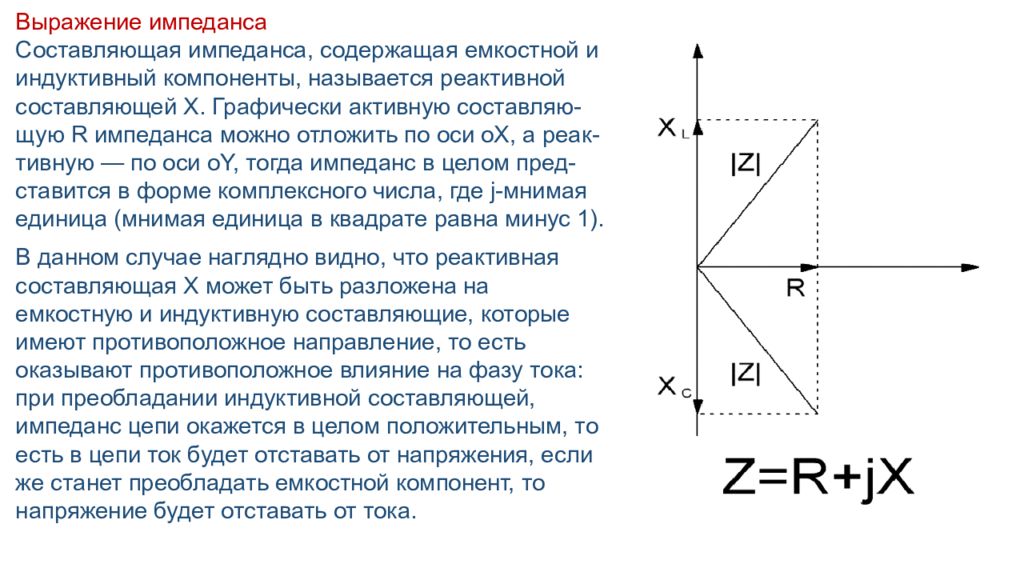
Выражение импеданса Составляющая импеданса, содержащая емкостной и индуктивный компоненты, называется реактивной составляющей X. Графически активную составляю- щую R импеданса можно отложить по оси оX, а реак-тивную — по оси оY, тогда импеданс в целом пред-ставится в форме комплексного числа, где j-мнимая единица (мнимая единица в квадрате равна минус 1). В данном случае наглядно видно, что реактивная составляющая X может быть разложена на емкостную и индуктивную составляющие, которые имеют противоположное направление, то есть оказывают противоположное влияние на фазу тока: при преобладании индуктивной составляющей, импеданс цепи окажется в целом положительным, то есть в цепи ток будет отставать от напряжения, если же станет преобладать емкостной компонент, то напряжение будет отставать от тока.
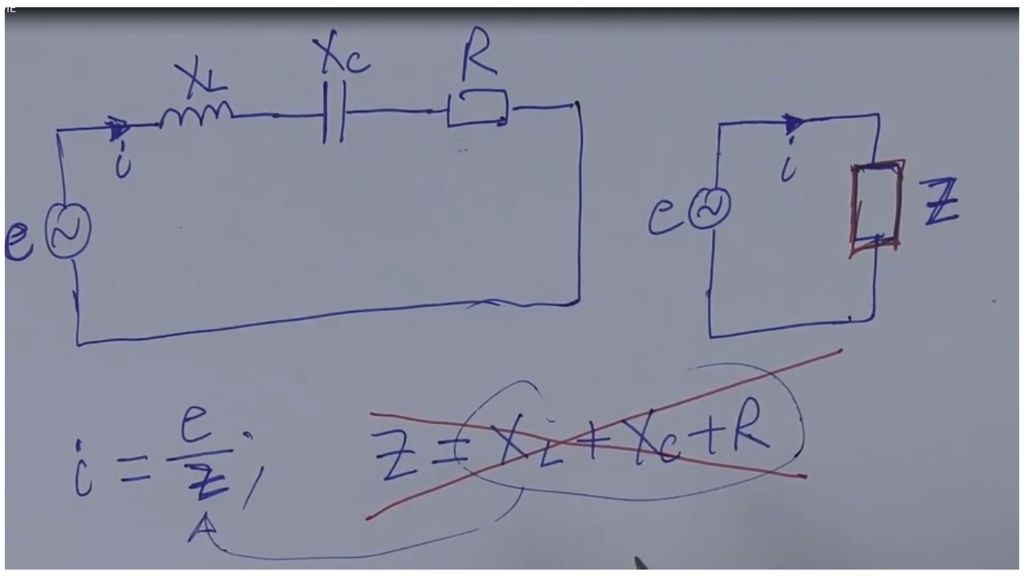
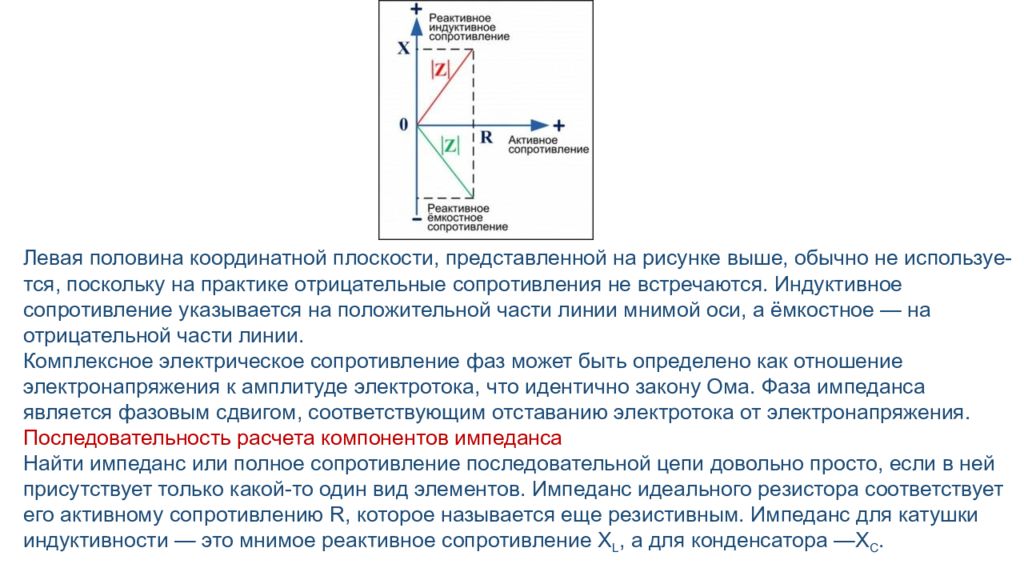
Левая половина координатной плоскости, представленной на рисунке выше, обычно не используе-тся, поскольку на практике отрицательные сопротивления не встречаются. Индуктивное сопротивление указывается на положительной части линии мнимой оси, а ёмкостное — на отрицательной части линии. Комплексное электрическое сопротивление фаз может быть определено как отношение электронапряжения к амплитуде электротока, что идентично закону Ома. Фаза импеданса является фазовым сдвигом, соответствующим отставанию электротока от электронапряжения. Последовательность расчета компонентов импеданса Найти импеданс или полное сопротивление последовательной цепи довольно просто, если в ней присутствует только какой-то один вид элементов. Импеданс идеального резистора соответствует его активному сопротивлению R, которое называется еще резистивным. Импеданс для катушки индуктивности — это мнимое реактивное сопротивление X L, а для конденсатора —Х С.
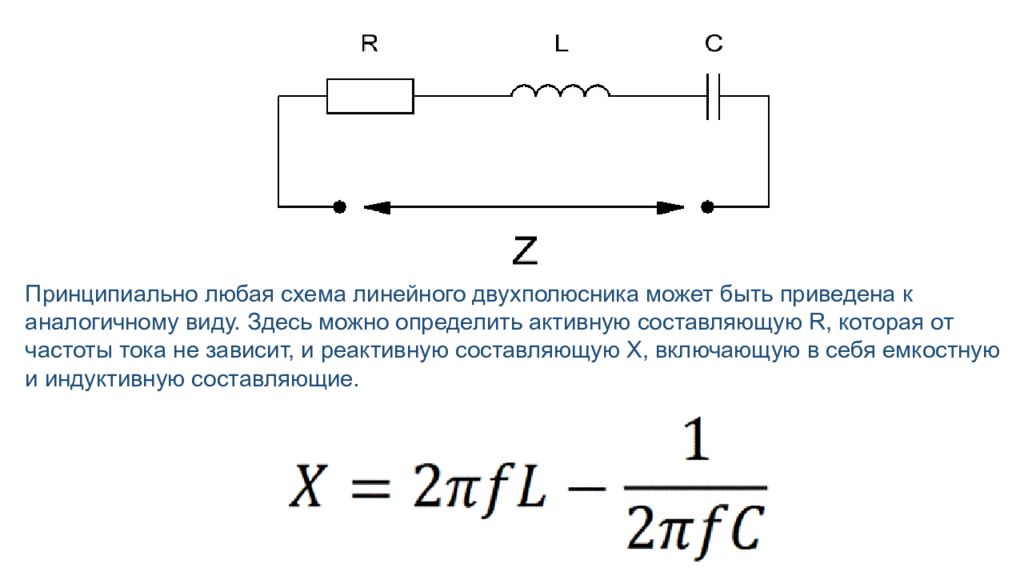
Принципиально любая схема линейного двухполюсника может быть приведена к аналогичному виду. Здесь можно определить активную составляющую R, которая от частоты тока не зависит, и реактивную составляющую X, включающую в себя емкостную и индуктивную составляющие.
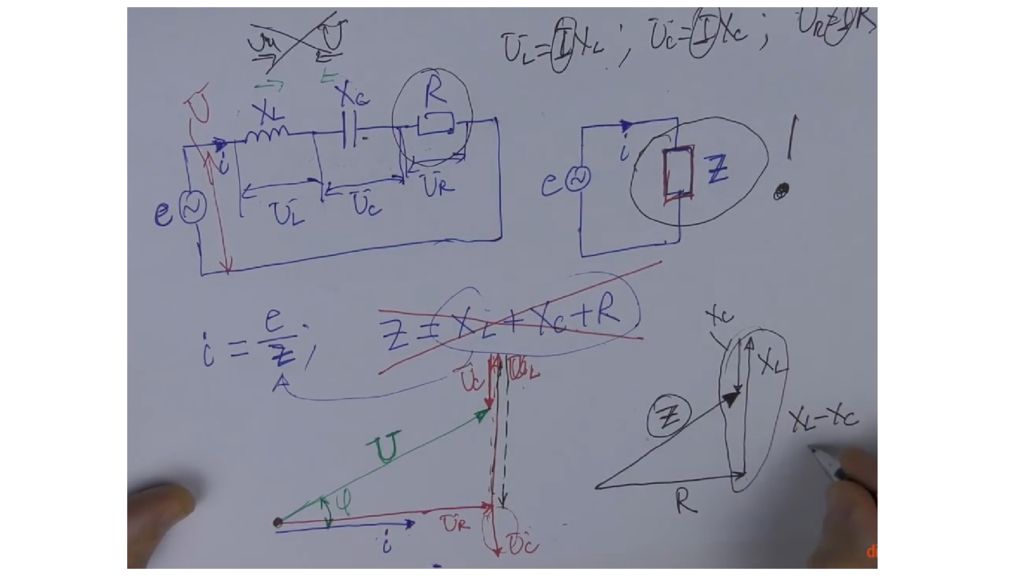
Из графической модели, где сопротивления представлены векторами, ясно, что модуль импеданса для заданной частоты синусоидального тока вычисляется как длина вектора, представляющего собой сумму векторов X и R. Измеряется импеданс в Омах.
Альтернативные термины Практически в описаниях цепей синусоидального переменного тока с точки зрения импеданса, можно встретить такие термины, как «активно-индуктивный характер нагрузки» или «активно-емкостная нагрузка» или «чисто активная нагрузка». Имеется ввиду следующее: 1. Если в цепи преобладает влияние индуктивности L, значит реактивная составляющая X положительна, при этом активная составляющая R мала — это индуктивная нагрузка. Пример индуктивной нагрузки — катушка индуктивности. 2. Если в цепи преобладает влияние емкости C, значит реактивная составляющая X отрицательна, при этом активная составляющая R мала — это емкостная нагрузка. Пример емкостной нагрузки — конденсатор. 3. Если в цепи преобладает активное сопротивление R, при этом реактивная составляющая X мала — это активная нагрузка. Пример активной нагрузки — лампа накаливания. 4. Если в цепи активная составляющая R значительна, но индуктивная составляющая преобладает над емкостной, то есть реактивная составляющая X положительна, нагрузку называют активно-индуктивной. Пример активно-индуктивной нагрузки — асинхронный двигатель. 5. Если в цепи активная R составляющая значительна, при этом емкостная составляющая преобладает над индуктивной, то есть реактивная составляющая X отрицательна, нагрузку называют активно-емкостной. Пример активно-емкостной нагрузки — блок питания люминесцентной лампы.
Импеданс - комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
