Первый слайд презентации: Институт математики, естественных и компьютерных наук кафедра физики
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ ТЕОРИЯ И ЗАДАЧИ ЕГЭ 2024 1 ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КОРАБЕЛЫ ПРИОНЕЖЬЯ
Слайд 2
Свободные гармонические (при отсутствии трения) Действует только квазиупругая возвращающая сила Амплитуда постоянна; механическая энергия сохраняется Классификация колебаний Свободные затухающие (при наличии сил трения) Действуют квазиупругая возвращающая сила и сила трения Амплитуда уменьшается; механическая энергия уменьшается, (переходит во внутреннюю энергию) Вынужденные (под действием внешней периодической вынуждающей силы) Действуют вынуждающая сила, квазиупругая возвращающая сила и сила трения Убыль механической энергии из-за трения восполняется за счёт работы внешней силы. Резонанс Автоколебания (источник энергии в системе; обязательно наличие обратной связи) Колебания происходят при периодическом поступлении энергии от источника внутри колебательной системы
Слайд 3
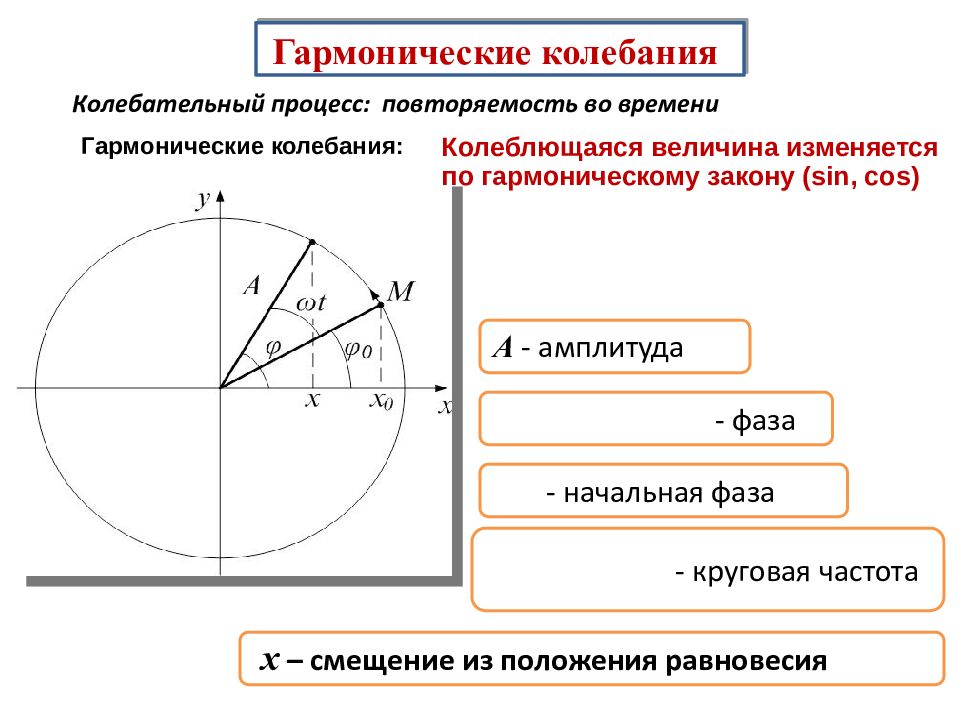
Гармонические колебания А - амплитуда - фаза - начальная фаза - круговая частота Колебательный процесс: повторяемость во времени Гармонические колебания: Колеблющаяся величина изменяется по гармоническому закону ( sin, cos ) x – смещение из положения равновесия
Слайд 4
Характеристики колебательного процесса Амплитуда ( А, x m ) – максимальное смещение тела от положения равновесия, м ( метр ) Период ( T ) – промежуток времени, в течение которого совершается одно полное колебание, с ( секунда ) Частота ( ν ) – количество колебаний за 1 с, Гц ( герц ) Циклическая частота ( ω ) – количество колебаний за 2π с, рад/с ( радиан в секунду ) Фаза ( φ ) – угловая мера времени (аргумент sin или cos), рад ( радиан ) T t N N 1 2 2 t 2 t t T T T
Слайд 5
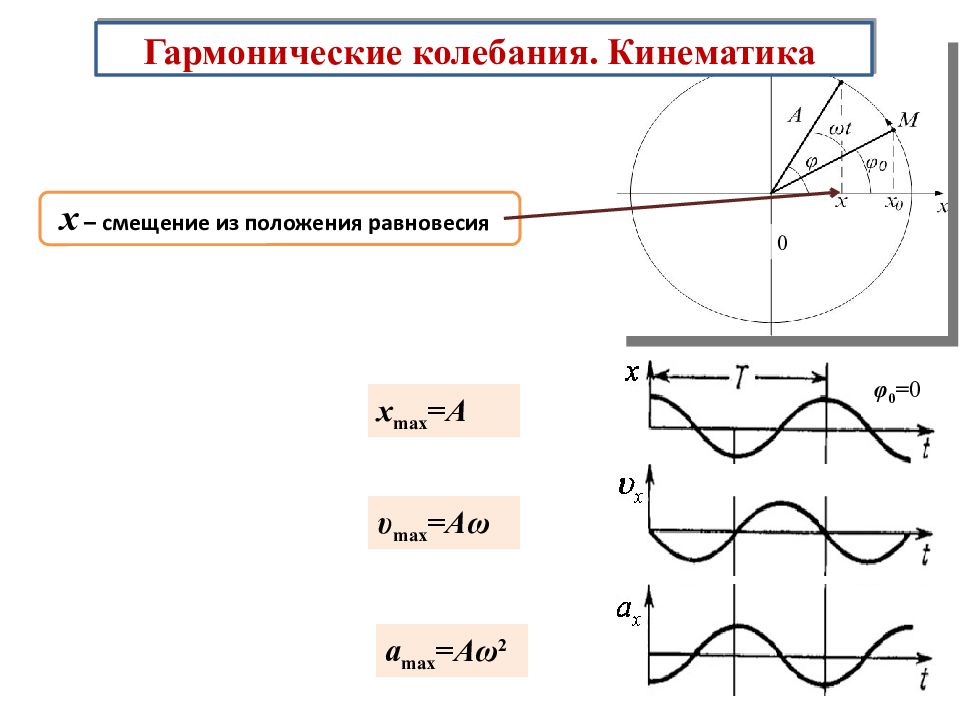
Гармонические колебания. Кинематика x – смещение из положения равновесия 0 x max =A υ max =A ω a max =A ω 2 φ 0 = 0
Слайд 6
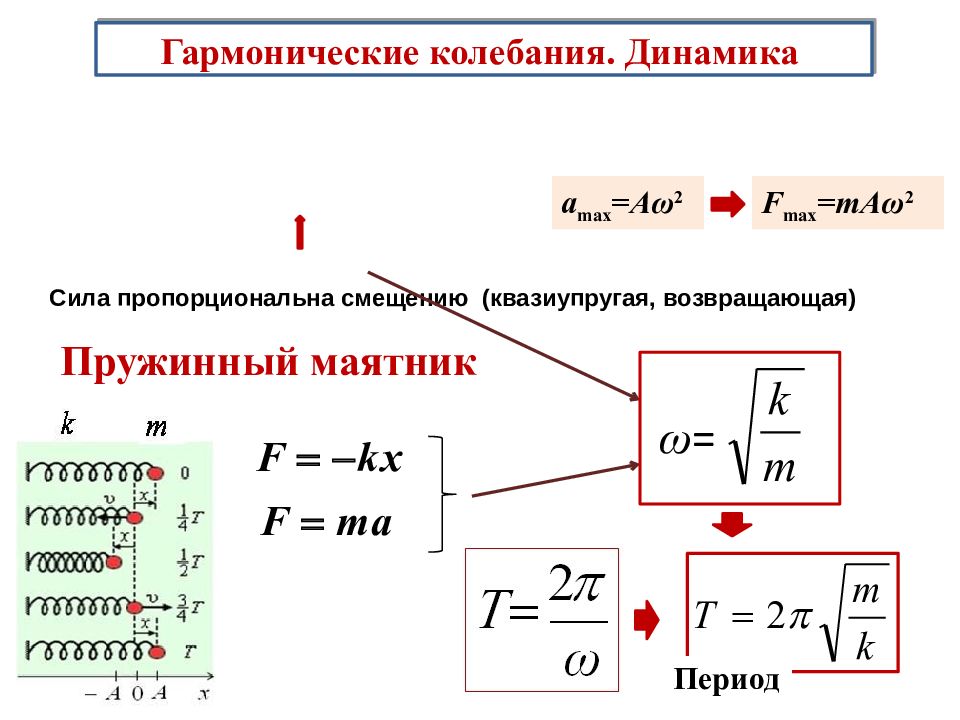
Гармонические колебания. Динамика a max =A ω 2 Сила пропорциональна смещению ( квазиупругая, возвращающая ) F max = mA ω 2 Пружинный маятник F kx F ma k m ω = m k T 2 Период
Слайд 7
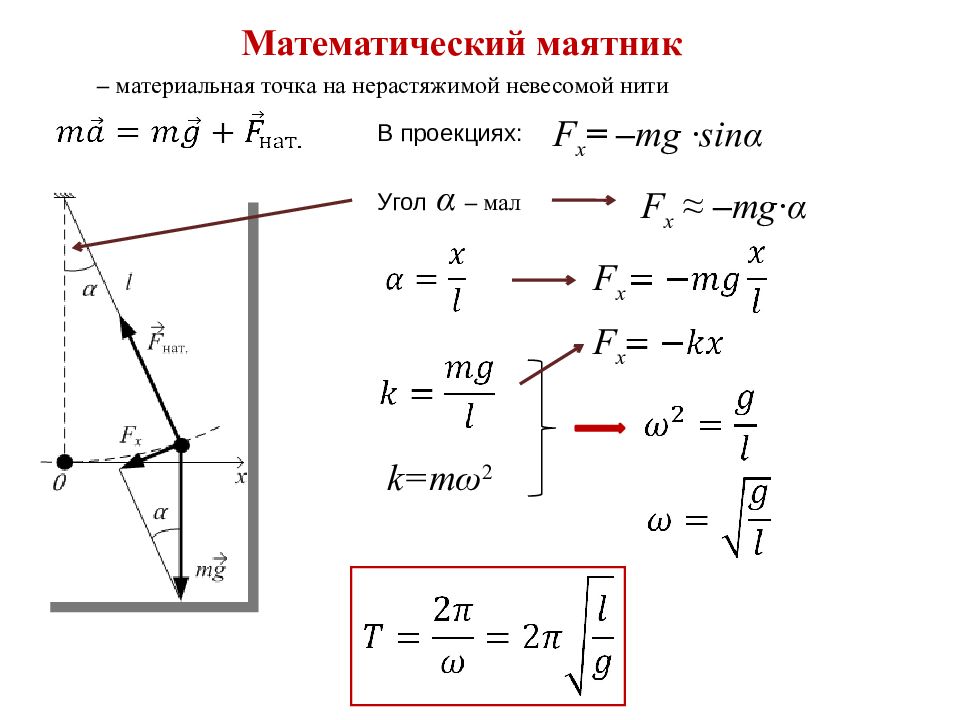
М атематический маятник – материальная точка на нерастяжимой невесомой нити F x = – mg · sin α k=m ω 2 Угол α – мал F x ≈ – mg · α В проекциях: F x F x
Слайд 8
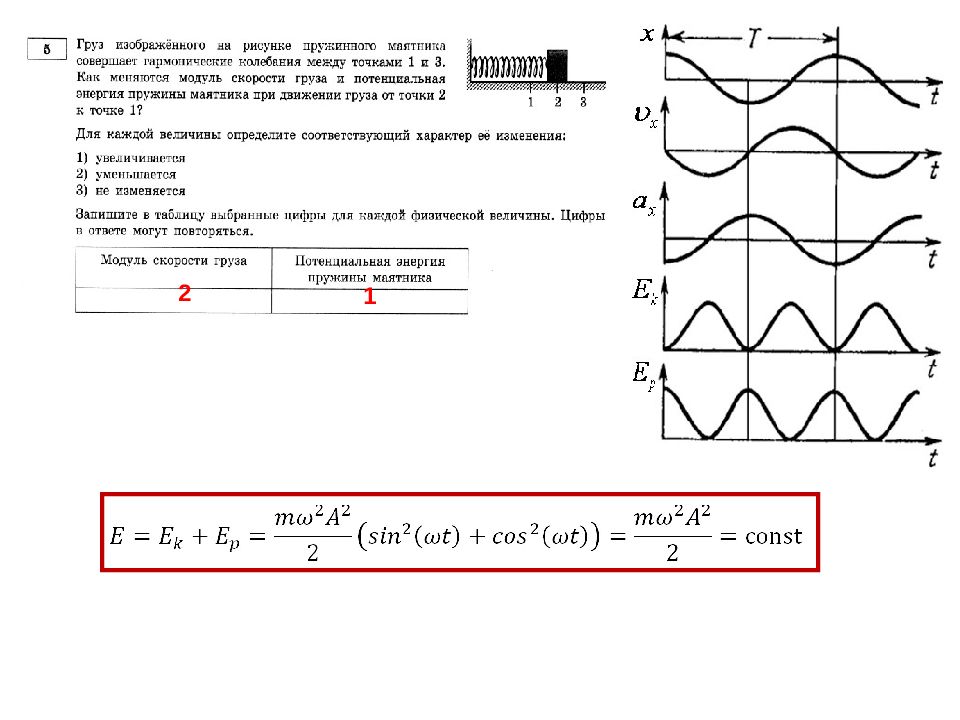
Гармонические колебания. Энергия Потенциальная энергия пружины: Кинетическая энергия груза: Полная энергия : E=const
Слайд 9: Гармонические колебания : резюме
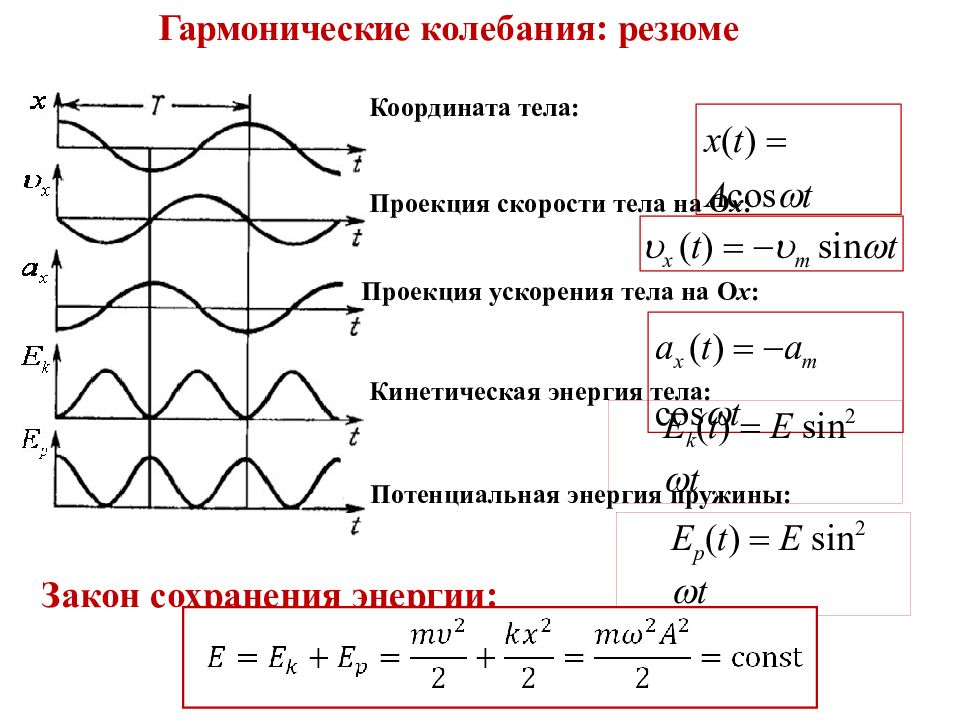
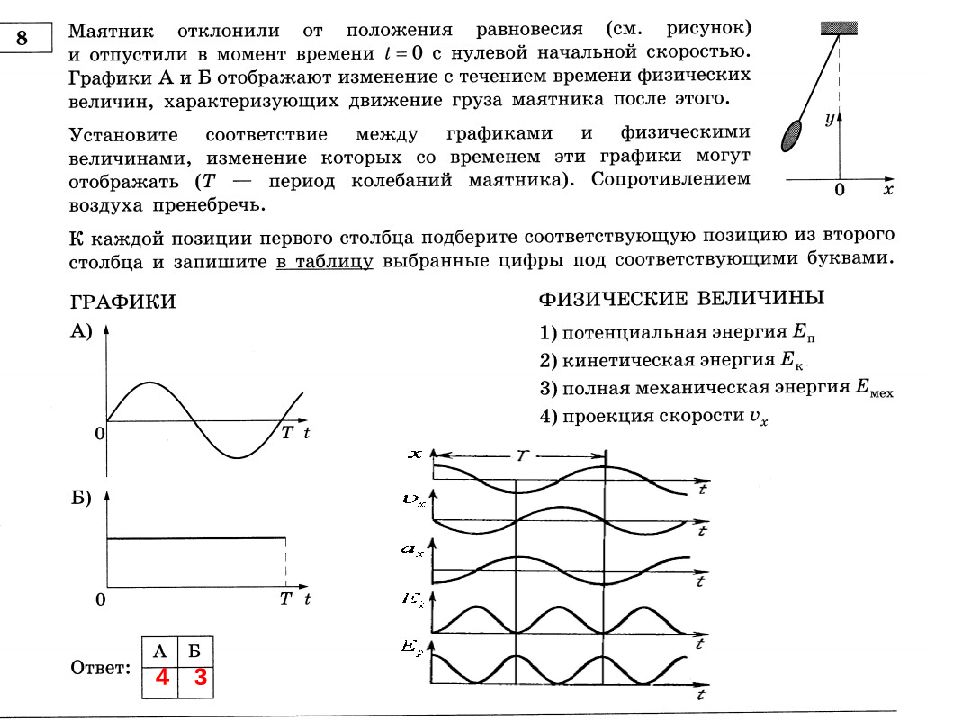
x ( t ) A cos t x ( t ) m sin t a x ( t ) a m cos t Гармонические колебания : резюме Координата тела: Проекция скорости тела на O x : Проекция ускорения тела на O x : Кинетическая энергия тела: E k ( t ) E sin 2 t Потенциальная энергия пружины: E p ( t ) E sin 2 t Закон сохранения энергии :
Слайд 10: Вынужденные колебания
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты внешней периодической силы ω с собственной частотой колебательной системы ω 0 : 0
Слайд 11
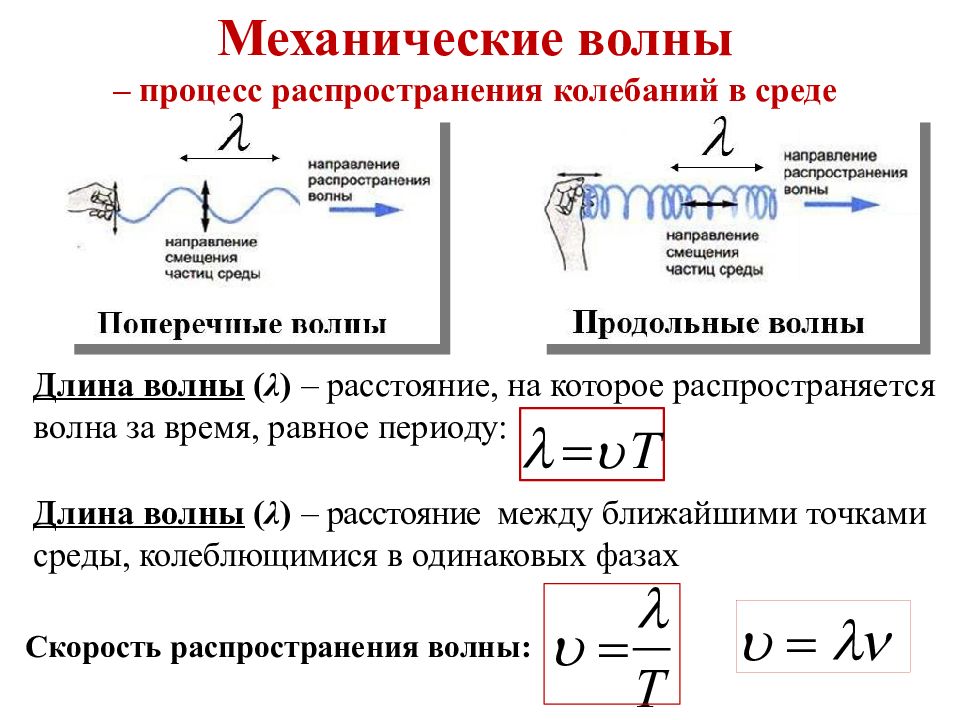
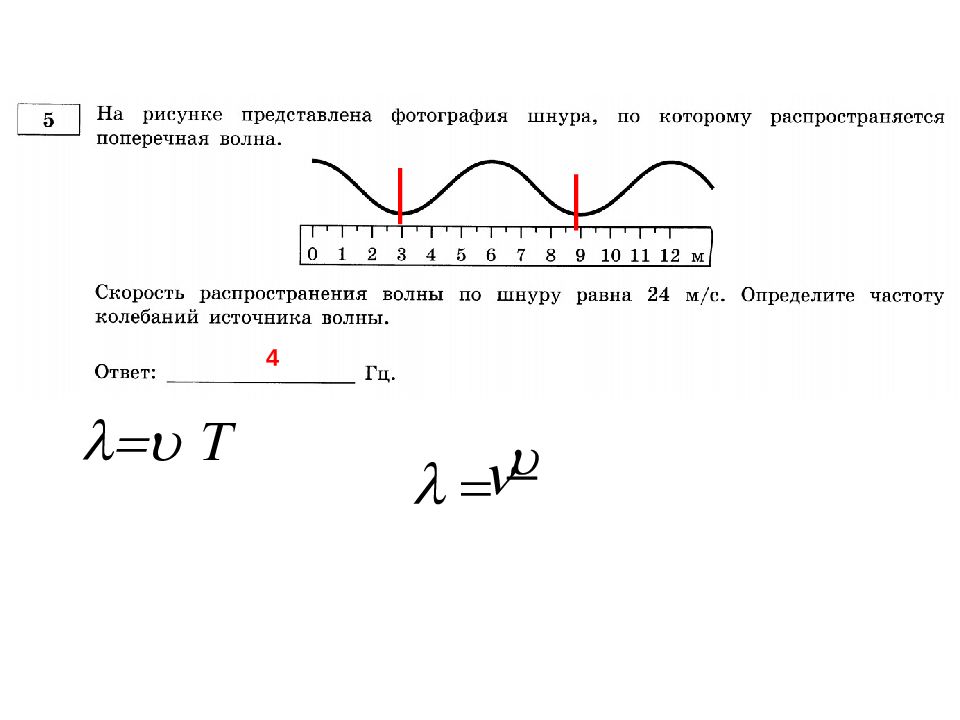
Механические волны – процесс распространения колебаний в среде Длина волны ( λ ) – расстояние, на которое распространяется волна за время, равное периоду: T Скорость распространения волны : T Длина волны ( λ ) – расстояние между ближайшими точками среды, колеблющимися в одинаковых фазах
Слайд 13: s A cos t
т. В : отставание по фазе Колебания начались позже на τ = т. О : К олебани я в т.В отстают по фазе от колебаний в т.0 на: Разность фаз колебаний двух точек: Уравнение бегущей волны υ l Замена переменной: t → ( t – τ )
Слайд 18
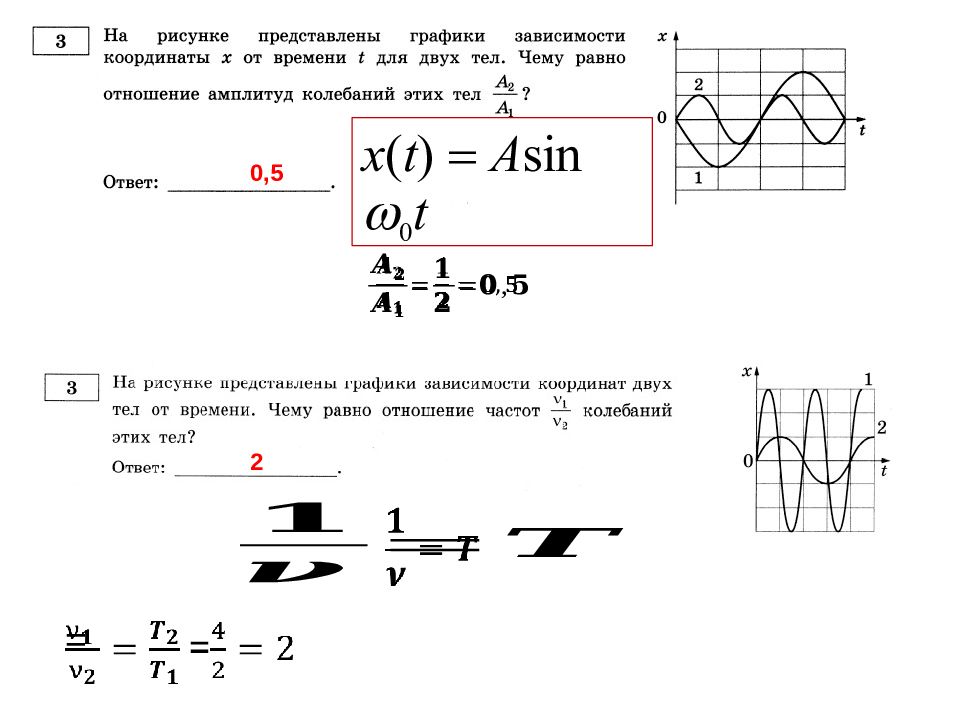
А 15 мм 0,015 м Т 4 с 2 2 kx 2 kA 2 E p 7 Из приведённого ниже списка выберите ВСЕ верные утверждения и запишите их номера Ответ: 12
Слайд 22
Скорость тела, совершающего гармонические колебания, x величины выражены в СИ. Определите амплитуду колебаний тела. меняется с течением времени по закону ( t ) 3 10 2 sin 6 t, где все x ( t ) m sin 0 t m с рад 0 3 10 2 м / с, 6 m A 0 0,005 м 5 мм A m 0 6 рад / c 3 10 2 м / с Ответ : 5 мм 1
Слайд 23
максимума? Ответ : 0,25 c Смещение груза пружинного маятника меняется с течением времени по закону x(t)=0,01sin2πt. Через какое минимальное время потенциальная энергия маятника достигнет своего x ( t ) A sin 0 t с рад 2 0 T 2 T 1 c kA 2 ( E p ) max 2 1 2 4 4 min t T 1 c 0,25 c 2
Слайд 24
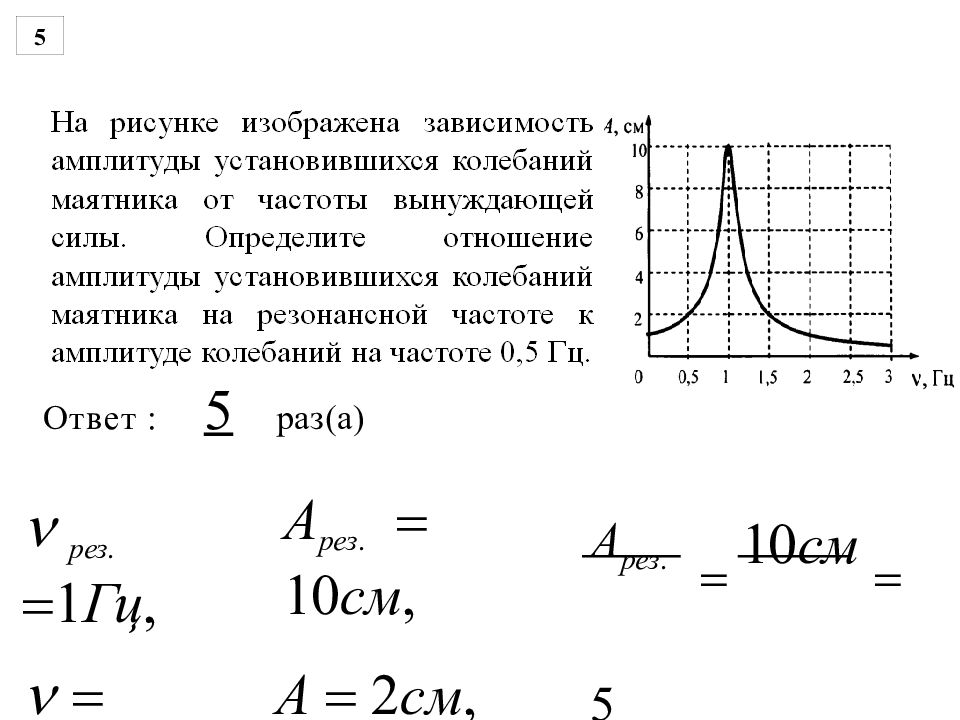
Ответ : 5 раз(а) рез. 1 Гц, 0,5 Гц, A рез. 10 см, A 2 см, A рез. 10 cм 5 A 2 см 5
Слайд 25
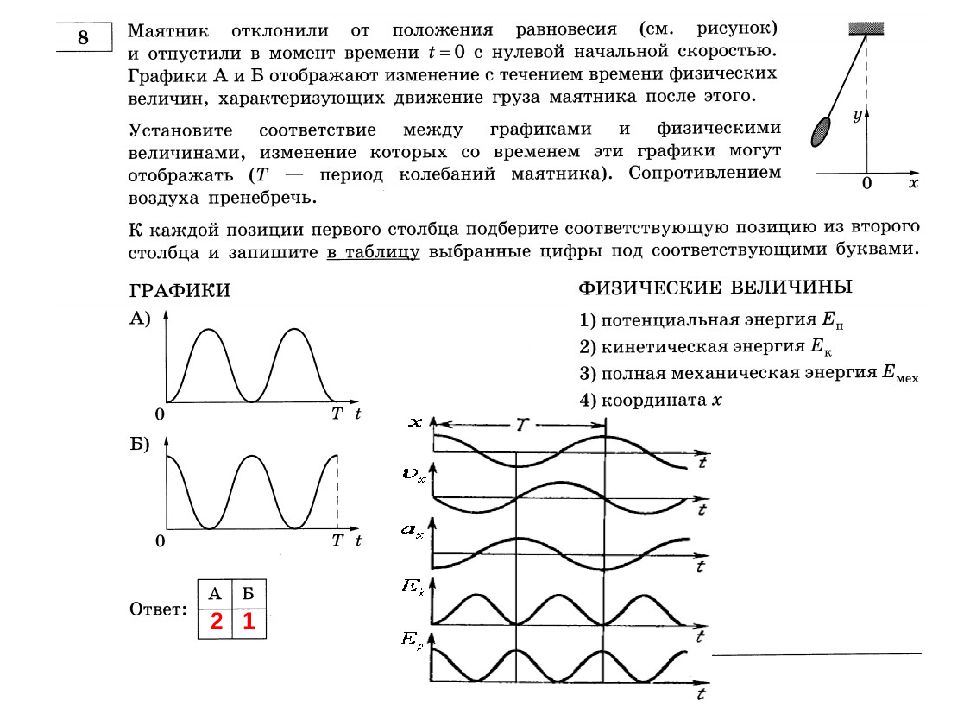
На рисунке представлен график гармонических колебаний математического маятника. Используя данные графика, выберите из предложенного перечня все верны е утверждения. Укажите их номера. При переходе из состояния, соответствующего точке А, в состояние, соответствующее точке Б, полная механическая энергия маятника уменьшается. Частота колебаний маятника равна 5 Гц. В состоянии, соответствующем точке В на графике, маятник имеет минимальную потенциальную энергию Точка В соответствует максимальному значению ускорения тела. Амплитуда колебаний маятника равна 0,2 м. В 8 А Б
Слайд 26
На рисунке представлен график гармонических колебаний математического маятника. Используя данные графика, выберите из T 0,2 с 1 1 5 Гц 2 4 предложенного перечня все верны е утверждения. Укажите их номера. При переходе из состояния, соответствующего точке А, в состояние, соответствующее точке Б, полная механическая энергия маятника уменьшается. Частота колебаний маятника равна 5 Гц. В состоянии, соответствующем точке В на графике, маятник имеет минимальную потенциальную энергию Точка В соответствует максимальному значению ускорения тела. Амплитуда колебаний маятника равна 0,2 м. a x ( t ) a m cos 0 t В 8 А Б
Слайд 30
F x ma x A sin t kA sin t m k x x A sin 2 t m F ma m 2 kx 2 kA 2 2 sin t 2 E p ( t ) 2 4 a 2 x x
Слайд 31
Грузик массой 100 г, подвешенный на лёгкой совершает свободные гармонические колебания. В пружине, таблице представлены координаты грузика через промежутки времени. Определите полную одинаковые механическую энергию данной колебательной системы. Ответ запишите в мДж, округли в до целых. t, с 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 x, см 6 3 0 3 6 3 0 6 Ответ : 11 мДж kA 2 E 2 А 3 см 0,03 м, Т 0,4 с 2 0 Т m k 2 0 2 0 k m, 0,0111 Дж 2 2 2 0,1 (0,03) 2 0,4 6,28 2 mA 2 T Е 0 2 2 2 2 mA 11
Слайд 38
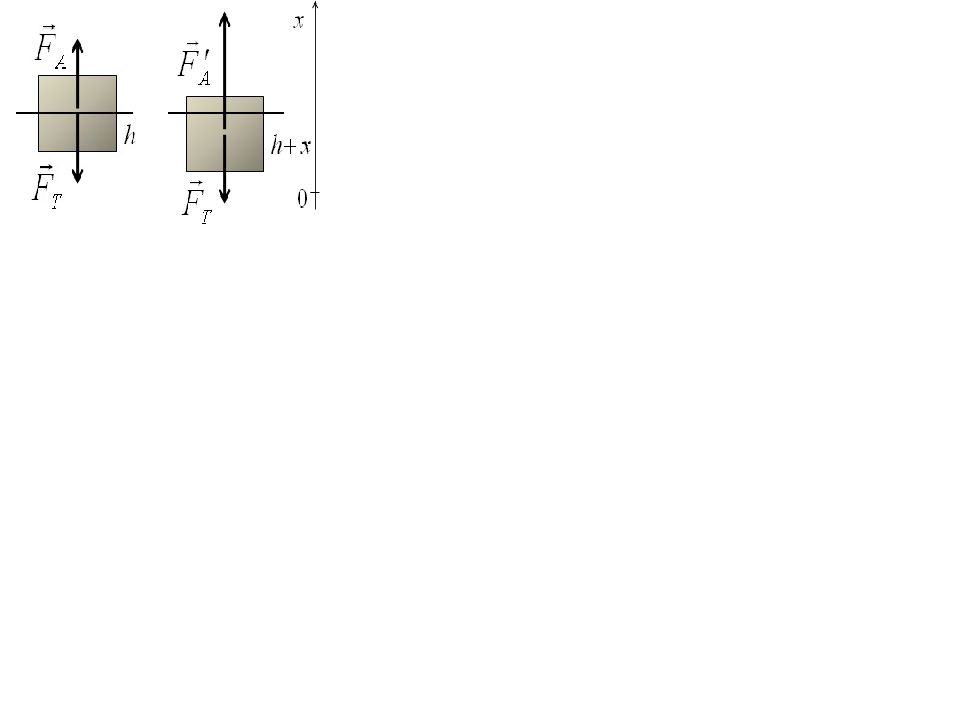
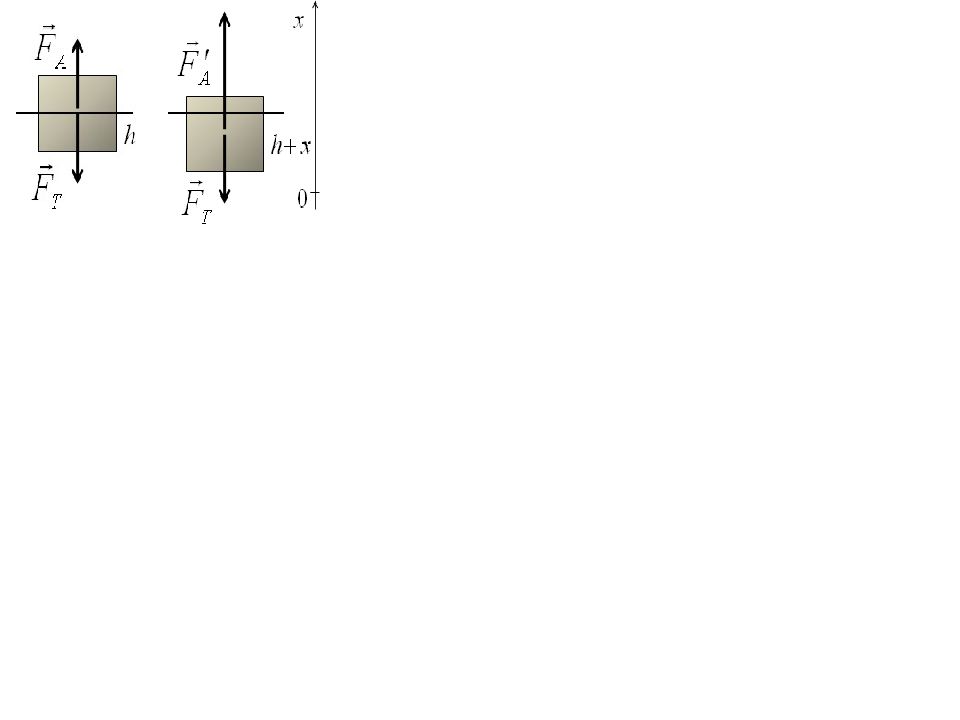
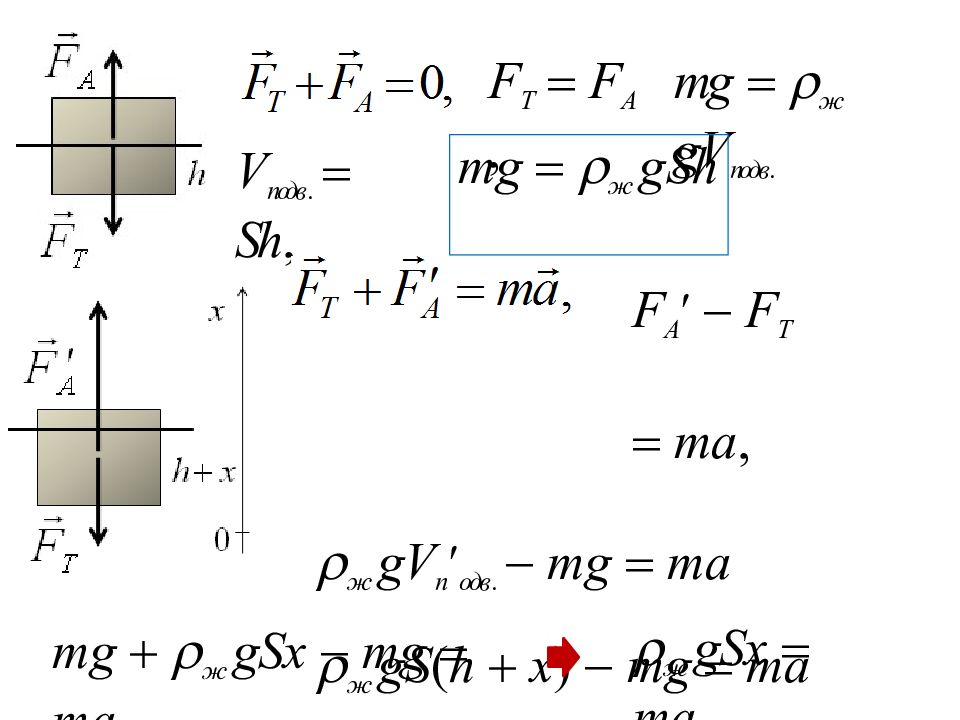
Однородный цилиндр массой 300 г с площадью поперечного сечения 10 см² плавает в воде, частично погрузившись в нее. Пренебрегая сопротивлением воды, определите период его малых вертикальных колебаний. Решение: I закон Ньютона II закон Ньютона
Слайд 41: mg ж gSh
F T F A, mg ж gV подв. V подв. Sh, mg ж gSh F A F T ma, ж gV п одв. mg ma ж gS ( h x ) mg ma ж gSh ж gSx mg ma mg ж gSx mg ma ж gSx ma
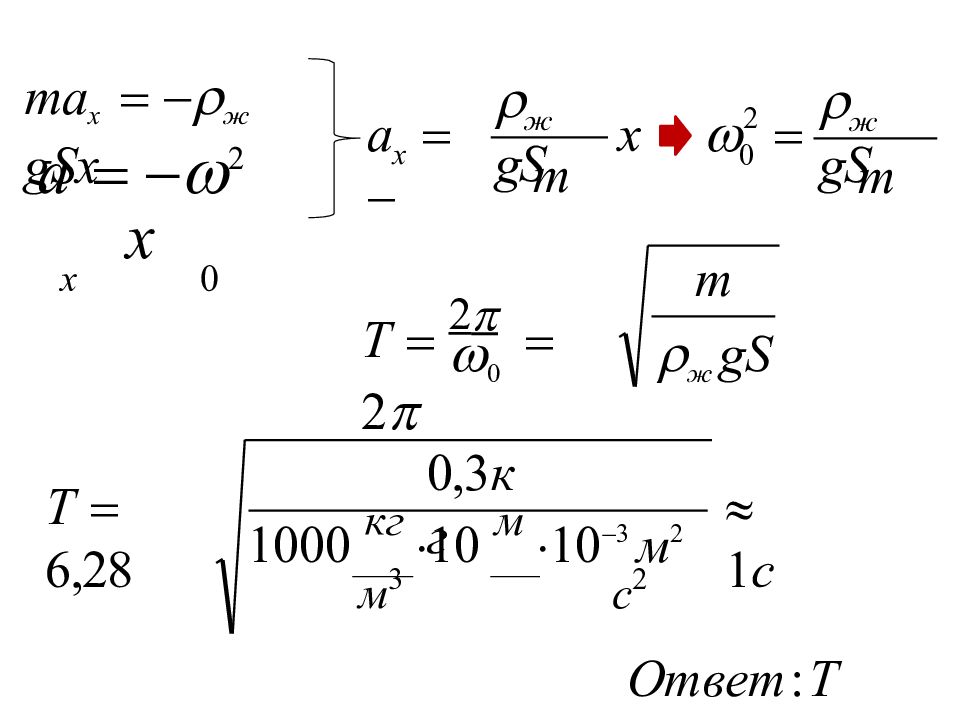
Слайд 42: ma x ж gSx
a 2 x x 0 x m ж gS x a m ж gS 2 0 m ж gS 0 T 2 2 1 с 0,3 кг T 6,28 1000 кг 10 м 10 3 м 2 м 3 с 2 От в е т : T 1 с