Слайд 2: Интерференция света (от лат. inter – взаимно, между собой и ferio – ударяю, поражаю) – пространственное перераспределение энергии света при наложении двух или нескольких световых волн. Интерференция волн – одно из основных свойств волн любой природы (упругих, электромагнитных, в т.ч. световых и др.). т акие характерные волновые явления, как излучение, распространение и дифракция, тоже связаны с интерференцией. Интерференцией света объясняются окраска тонких масляных пленок на поверхности воды, металлический отлив в окраске крыльев насекомых и птиц, появление цветов побежалости на поверхности металлов, голубоватый цвет просветленных линз оптических приборов и пр. Некоторые явления интерференции света исследовались еще И. Ньютоном в XVII в., но не могли быть им объяснены с точки зрения его корпускулярной теории. Правильное объяснение интерференции света как типично волнового явления было дано в начале XIX в. Т. Юнгом и О. Френелем
Слайд 3
Необходимыми условиями возникновения интерференции являются монохроматичность и когерентность световых потоков Монохроматичность световых волн означает неизменность во времени их длин и частот колебаний Любой световой поток можно представить как суперпозицию монохроматичных волн
Слайд 4
Стабильную интерференционную картину можно получить используя когерентные источники Когерентность источников излучения означает, что колебательные процессы протекают в них согласованно во времени
Слайд 5
Когерентное излучение можно получить двумя способами От нескольких независимых источников света высокой степени монохроматичности (лазеров) Выделяя лучи от одного и того же источника Второй способ получил наибольшее распространение
Слайд 6
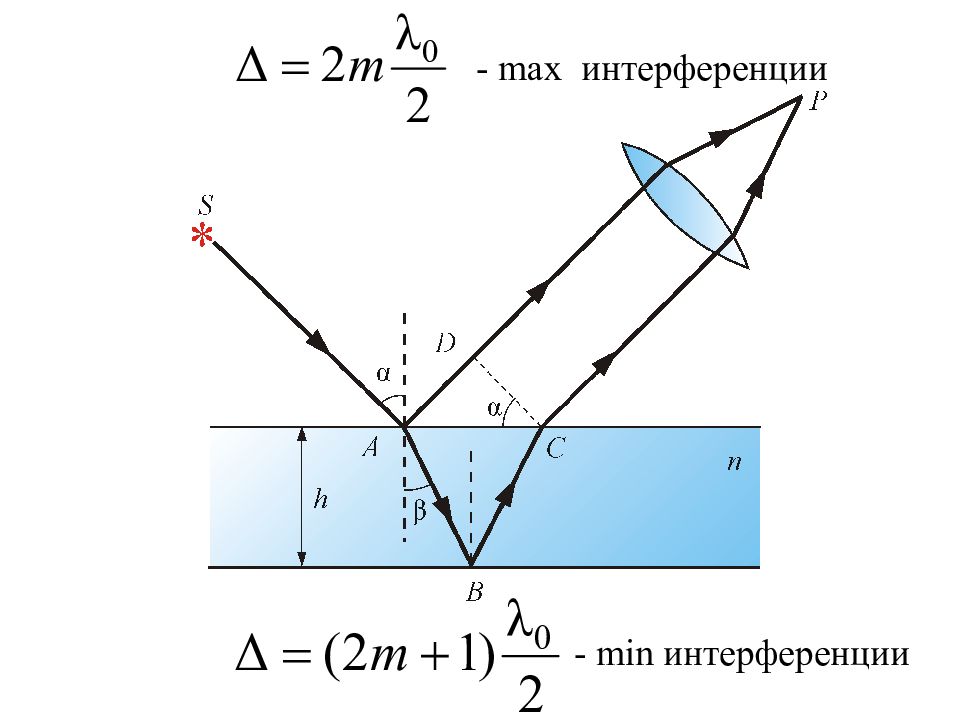
Рисунок 7.3 Первая волна Разность фаз двух когерентных волн - Оптическая разность хода - L – оптическая длина пути; s – геометрическая длина пути; n – показатель преломления среды. вторая Рассмотрим интерференцию двух когерентных волн:
Слайд 7
Условие максимума и минимума интерференции: Если оптическая разность хода равна целому числу длин волн - условие интерференционного максимума. Если оптическая разность хода равна полу-целому числу длин волн - условие интерференционного минимума.
Слайд 8
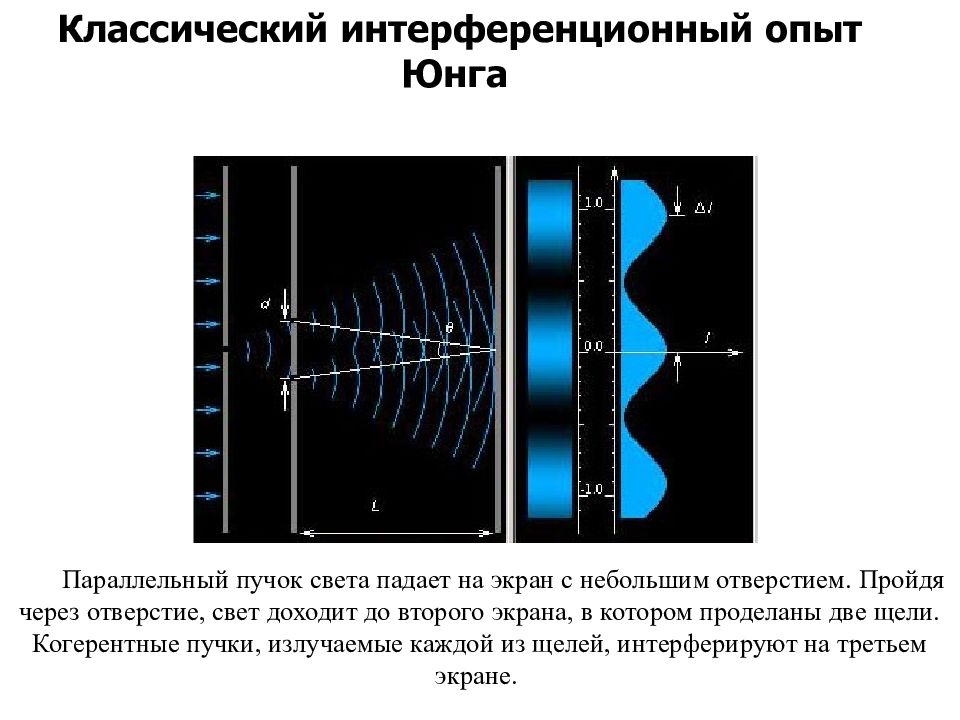
Параллельный пучок света падает на экран с небольшим отверстием. Пройдя через отверстие, свет доходит до второго экрана, в котором проделаны две щели. Когерентные пучки, излучаемые каждой из щелей, интерферируют на третьем экране. Классический интерференционный опыт Юнга
Слайд 9
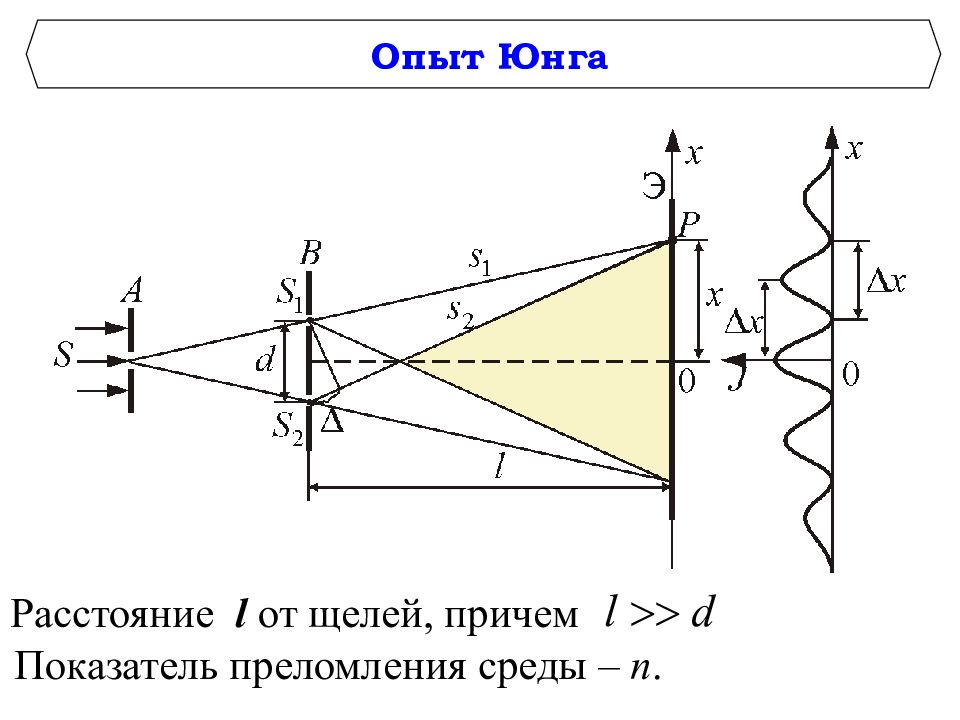
Опыт Юнга Расстояние l от щелей, причем Показатель преломления среды – n.
Слайд 10
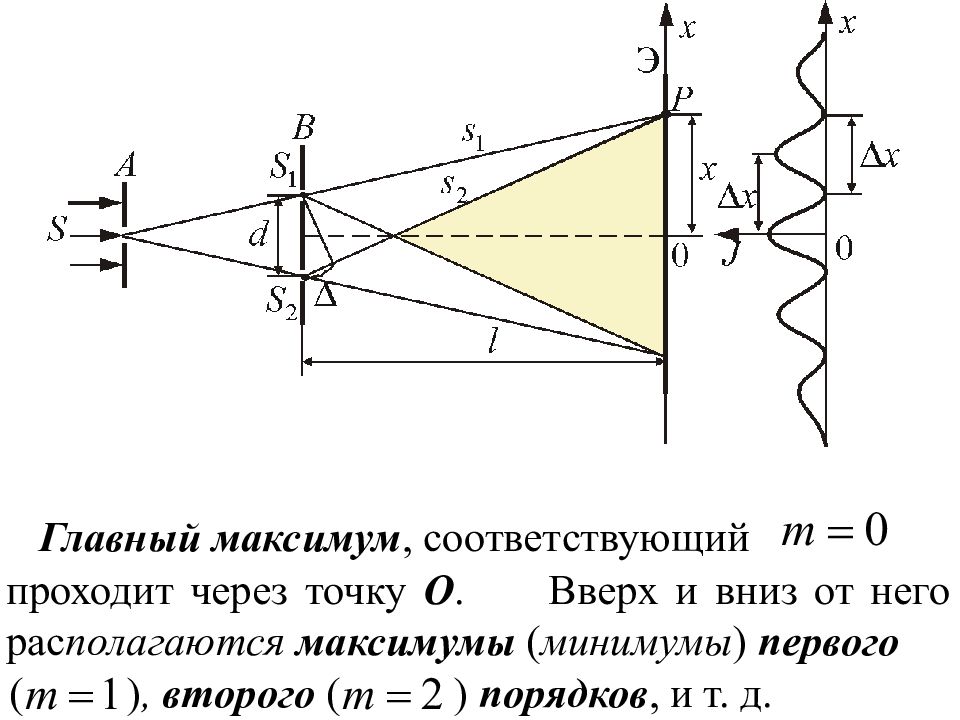
Главный максимум, соответствующий проходит через точку О. Вверх и вниз от него рас полагаются максимумы ( минимумы ) первого ( ), второго ( ) порядков, и т. д.
Слайд 11
Расстояние между двумя соседними максимумами (или минимумами) равно Максимумы интенсивности будут наблюдаться в координатах : ( m = 0, 1, 2, …), а минимумы – в координатах: - ширина интерференционной полосы. Измерив , зная l и d, можно вычислить длину волны λ. Именно так вычисляют длины волн разных цветов в спектроскопии.
Слайд 12
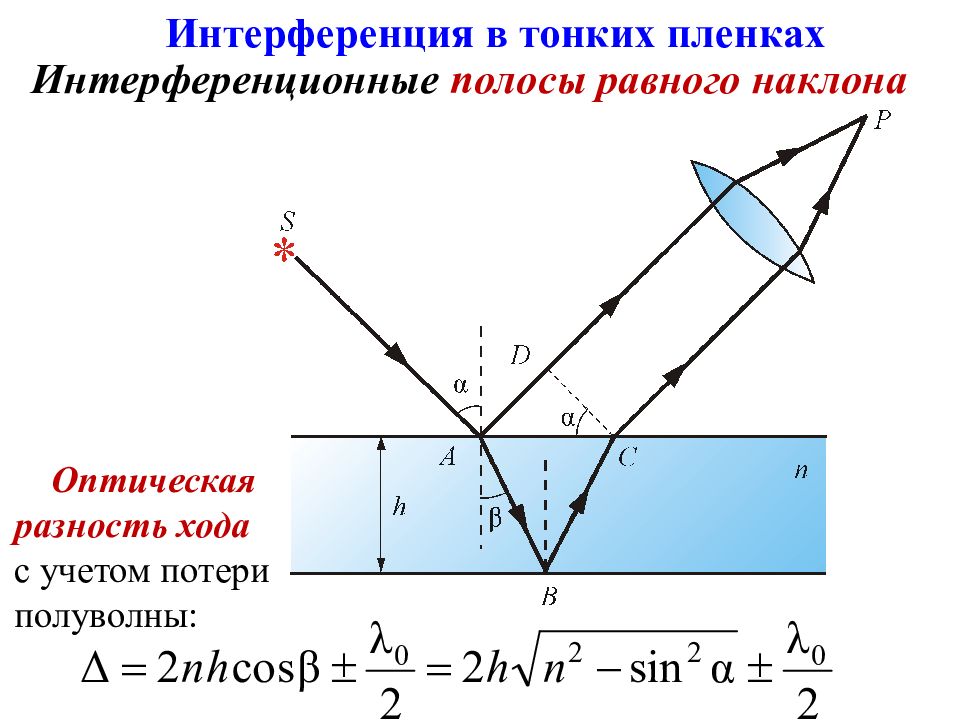
Интерференционные полосы равного наклона Интерференция в тонких пленках Оптическая разность хода с учетом потери полуволны:
Слайд 14
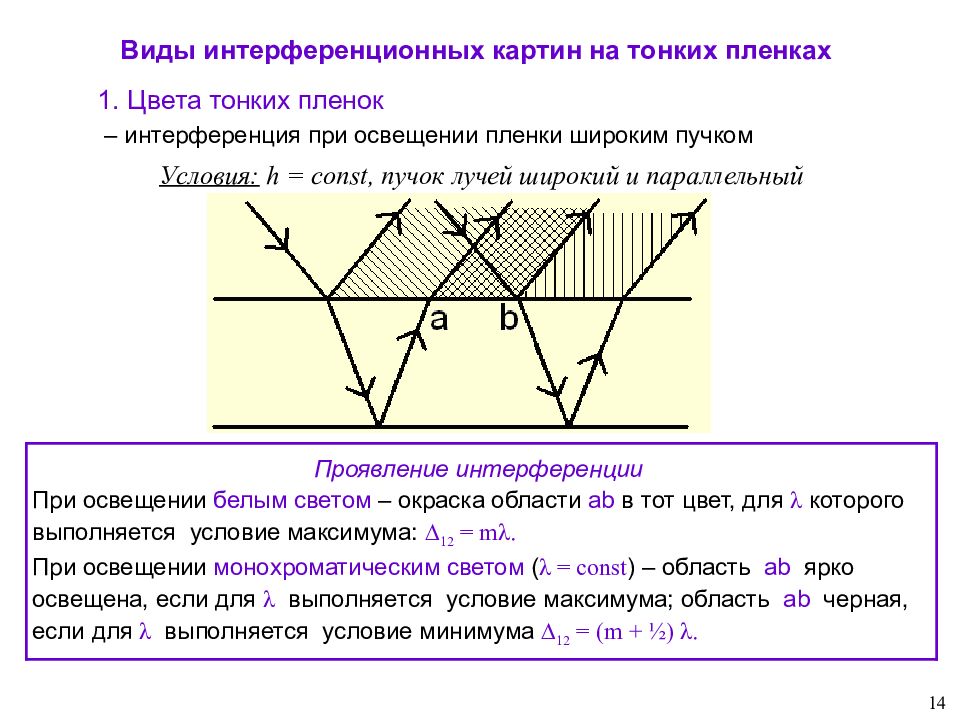
14 Виды интерференционных картин на тонких пленках Условия: h = const, пучок лучей широкий и параллельный 1. Цвета тонких пленок – интерференция при освещении пленки широким пучком Проявление интерференции При освещении белым светом – окраска области ab в тот цвет, для λ которого выполняется условие максимума: ∆ 12 = mλ. При освещении монохроматическим светом ( λ = const ) – область ab ярко освещена, если для λ выполняется условие максимума; область ab черная, если для λ выполняется условие минимума ∆ 12 = (m + ½) λ.
Слайд 15
Интерференция от клина. Полосы равной толщины В белом свете интерференционные полосы, при отражении от тонких пленок - окрашены. Поэтому такое явление называют цвета тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.
Слайд 17
Изменение картины интерференции по мере уменьшения толщины мыльной пленки
Слайд 18
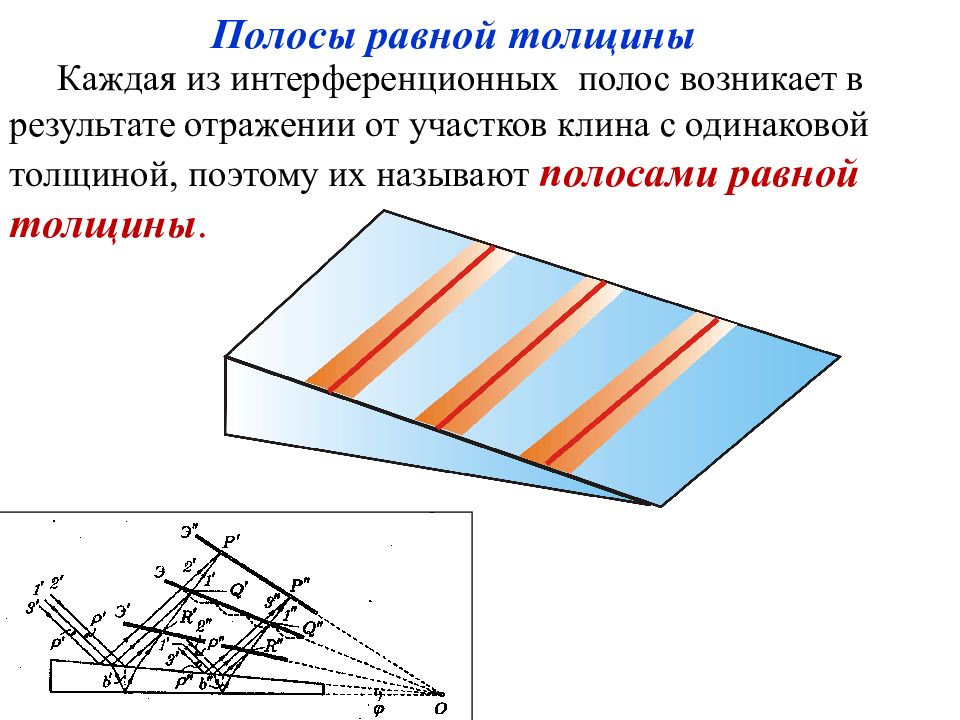
Каждая из интерференционных полос возникает в результате отражении от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины. Рис. 7.15 Полосы равной толщины
Слайд 19
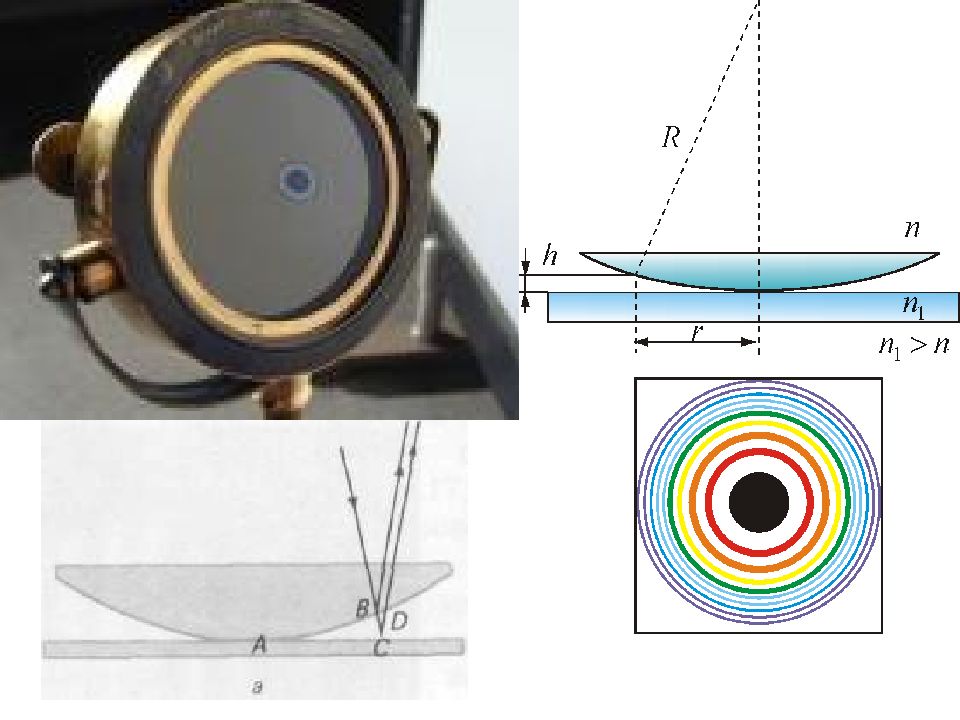
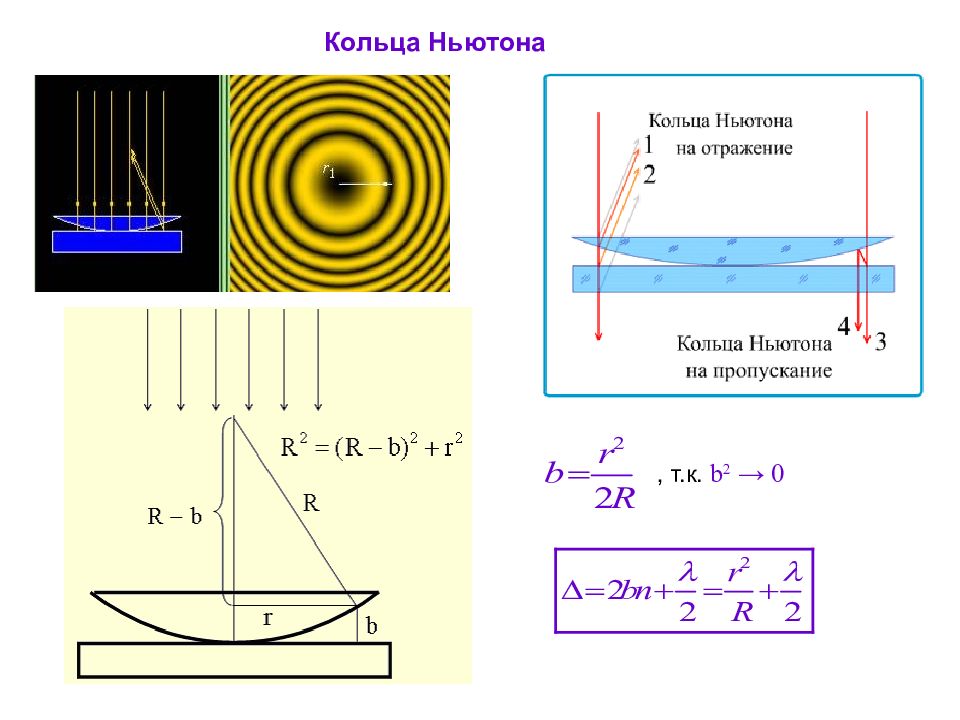
Кольца Ньютона Ньютон объяснил это явление на основе корпускулярной теории света. Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла, называют кольцами Ньютона.
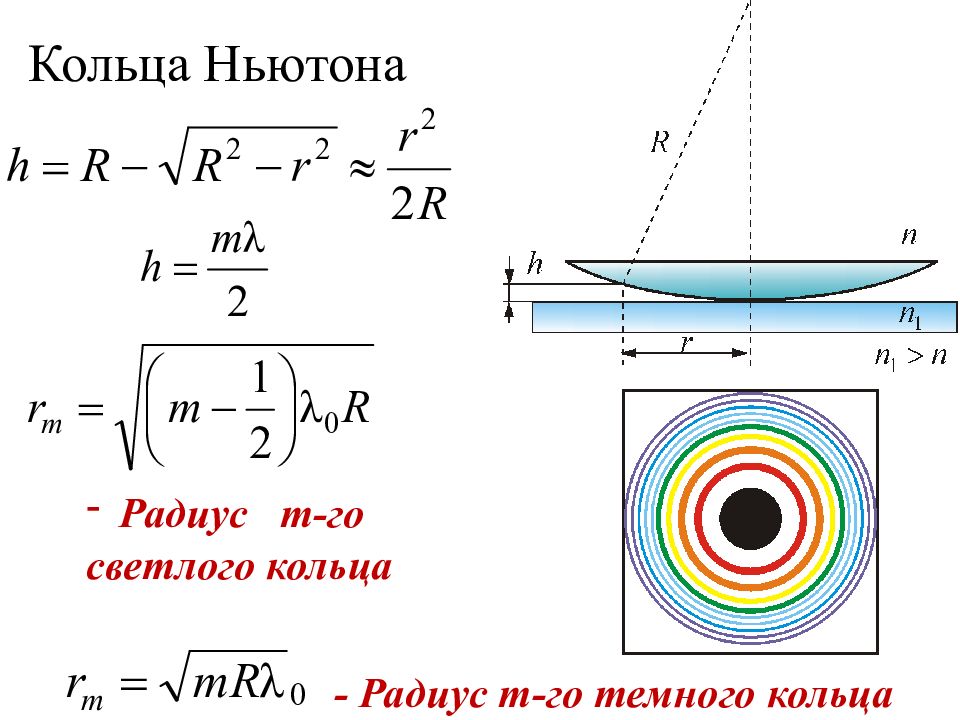
Слайд 21: Кольца Ньютона
- Радиус m-го темного кольца Радиус m -го светлого кольца
Слайд 23
Условие максимума (светлые кольца) ∆ = m λ, где m – целое число. - радиус m -го светлого кольца в отраженном свете (и темного – в прошедшем ) Условие минимума (темные кольца) ∆ = (m + ½) λ. - радиус m -го темного кольца в отраженном свете (и светлого – в прошедшем ) Кольца Ньютона в зеленом и красном свете Пример применения – проверка качества шлифовки линз.
Слайд 24: Использование интерференции
Явление интерференции нашло широкое практическое применение Создание просветлённых покрытий Измерение малых расстояний и перемещений Контроль поверхности Измерение показателя преломления Голография
Слайд 25
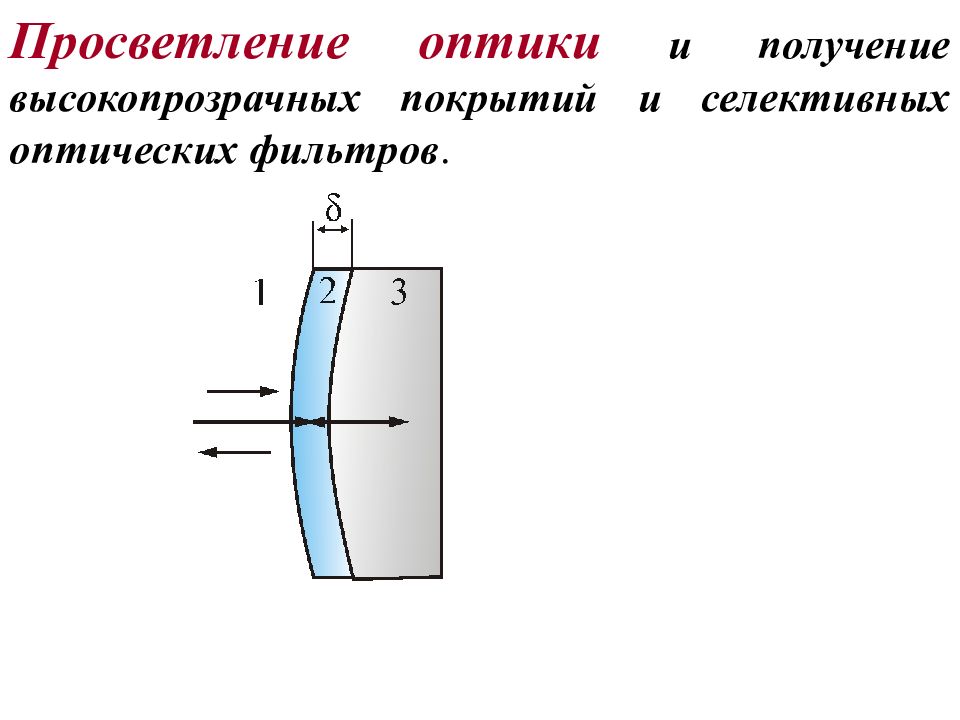
Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров.
Слайд 26
m a x пропускания света в рабочий объем Просветление линз и солнечных батарей d n Тонкая пленка окислов Min интерференции
Слайд 27: Дифракция света
- приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Дифракция света сопровождается интерференцией. Интерферируют волны, обогнувшие препятствие ( опыт Юнга ).
Слайд 28
Дифракционная картина – система чередующихся светлых и темных колец, если препятствие круг или отверстие. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
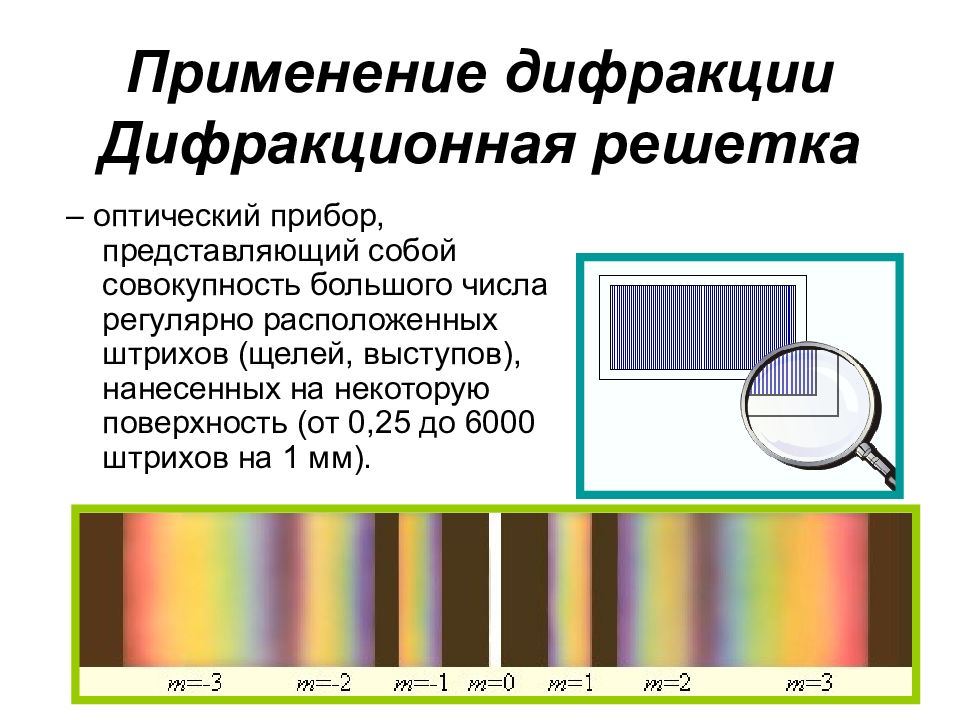
Слайд 29: Применение дифракции Дифракционная решетка
– оптический прибор, представляющий собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесенных на некоторую поверхность (от 0,25 до 6000 штрихов на 1 мм).
Слайд 30: Применение дифракции Дифракционная решетка
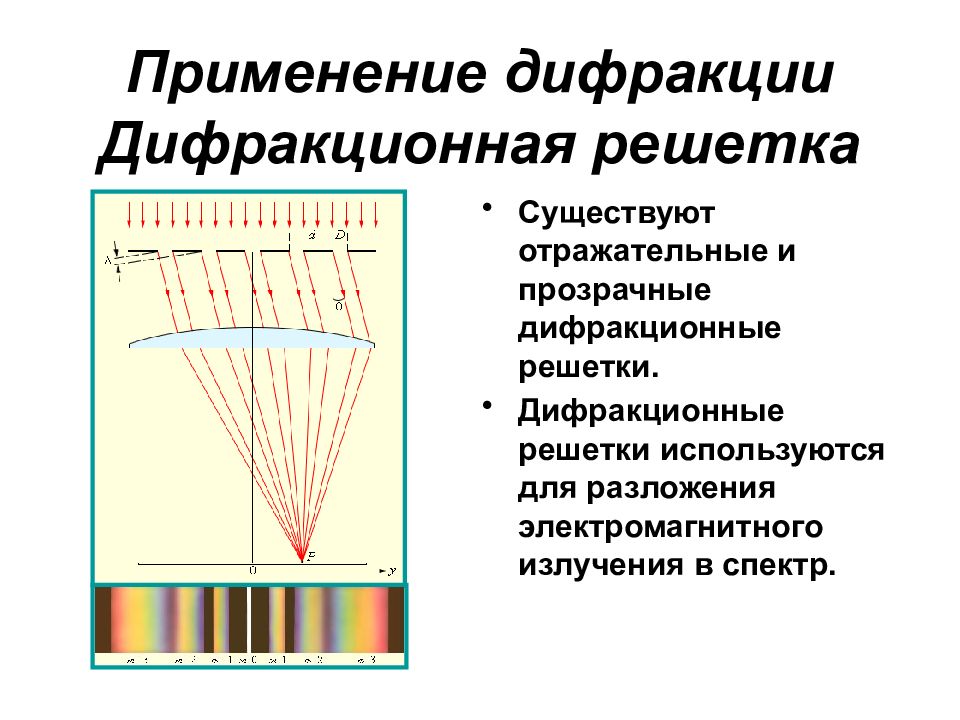
Существуют отражательные и прозрачные дифракционные решетки. Дифракционные решетки используются для разложения электромагнитного излучения в спектр.
Слайд 31: Дифракционная решетка
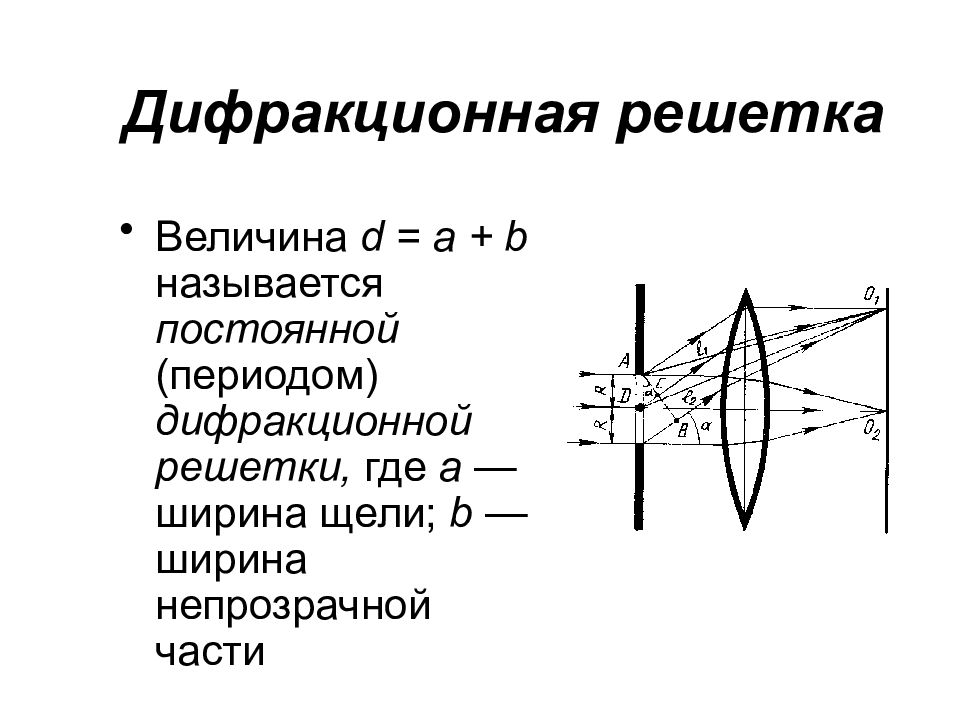
Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части
Слайд 32: Дифракционная решетка
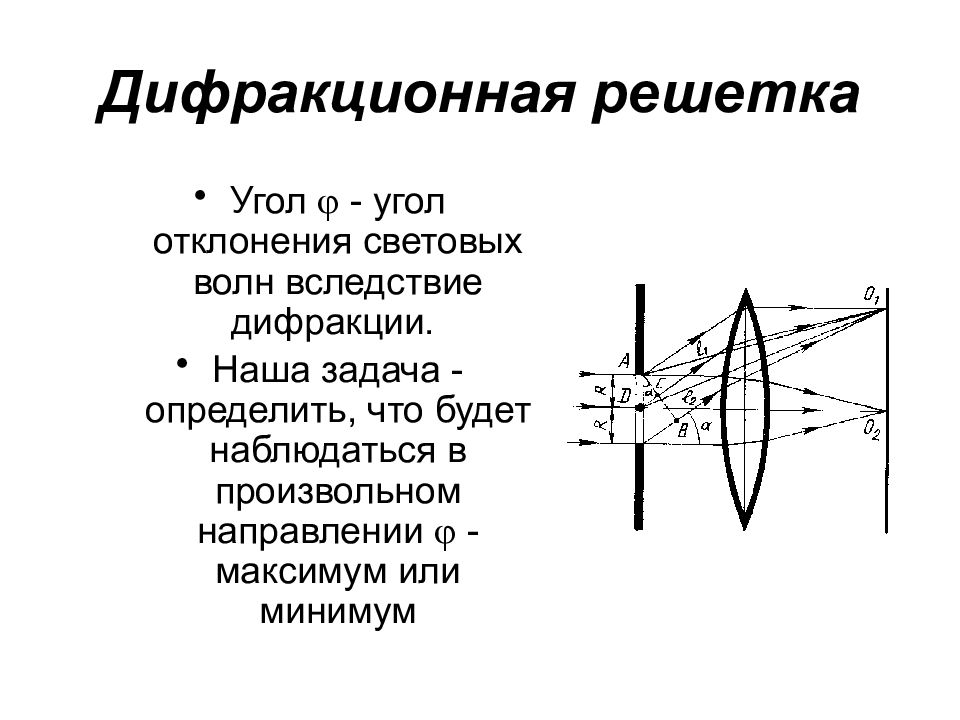
Угол - угол отклонения световых волн вследствие дифракции. Наша задача - определить, что будет наблюдаться в произвольном направлении - максимум или минимум
Слайд 33: Дифракционная решетка
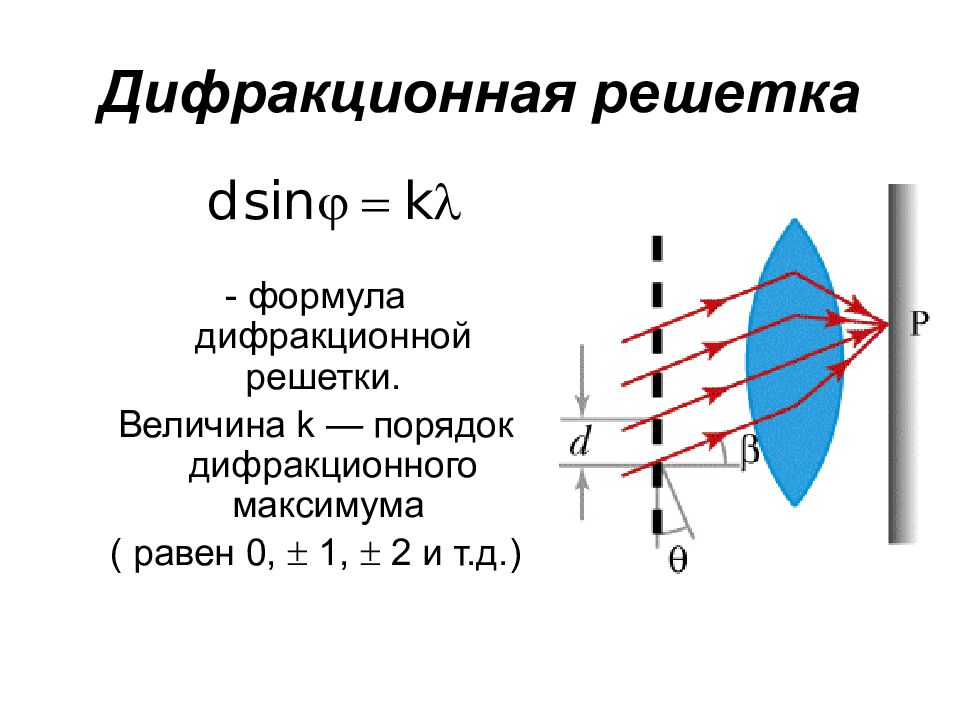
- формула дифракционной решетки. Величина k — порядок дифракционного максимума ( равен 0, 1, 2 и т.д.)
Последний слайд презентации: Интерференция света
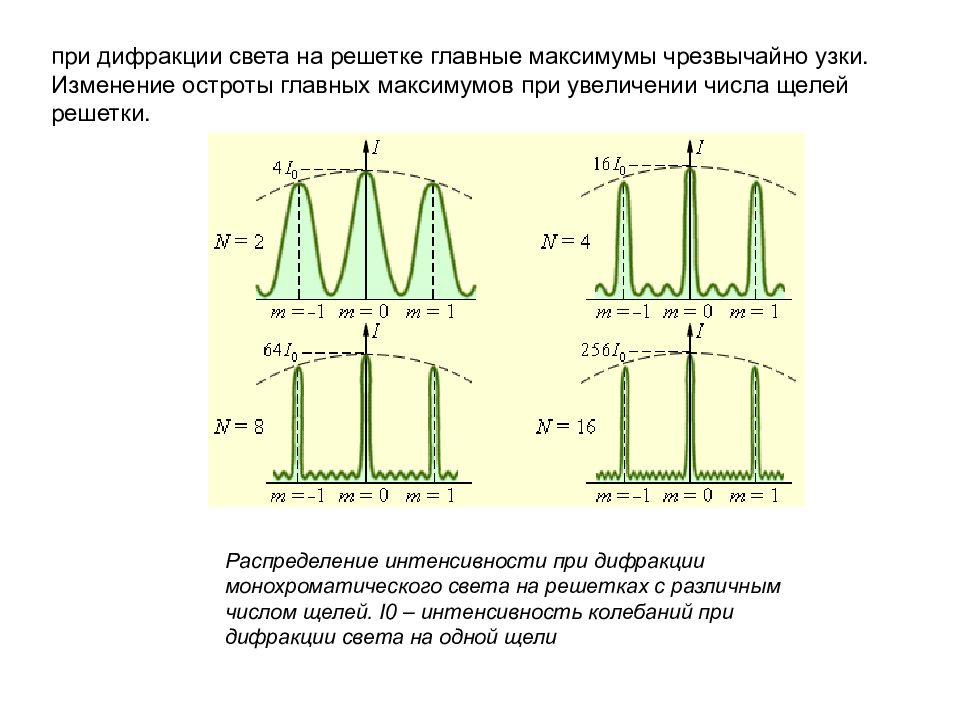
при дифракции света на решетке главные максимумы чрезвычайно узки. Изменение остроты главных максимумов при увеличении числа щелей решетки. Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I0 – интенсивность колебаний при дифракции света на одной щели