Первый слайд презентации: История
Термин «граф» впервые появился в книге выдающегося венгерского математика Д. Кёнига в 1936 г, хотя начальные задачи теории графов восходят еще к Леонарду Эйлеру ( XVIII в.). Л. Эйлер в 1736 году опубликовал решение задачи о Кенигсбергских мостах.
Слайд 2: История возникновения графов
Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая задачу о кенигсбергских мостах. Сегодня эта задача стала классической. содержание
Слайд 3: Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград ) расположен на реке Прегель. В пределах города река омывает два острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены. Дальше
Слайд 4: Задача о Кенигсбергских мостах
Кенигсбергцы предлагали приезжим следующую задачу: пройти по всем мостам и вернуться в начальный пункт, причём на каждом мосту следовало побывать только один раз. Дальше
Слайд 6: Задача о Кенигсбергских мостах
Пройти по Кенигсбергским мостам, соблюдая заданные условия, нельзя. Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа. дальше
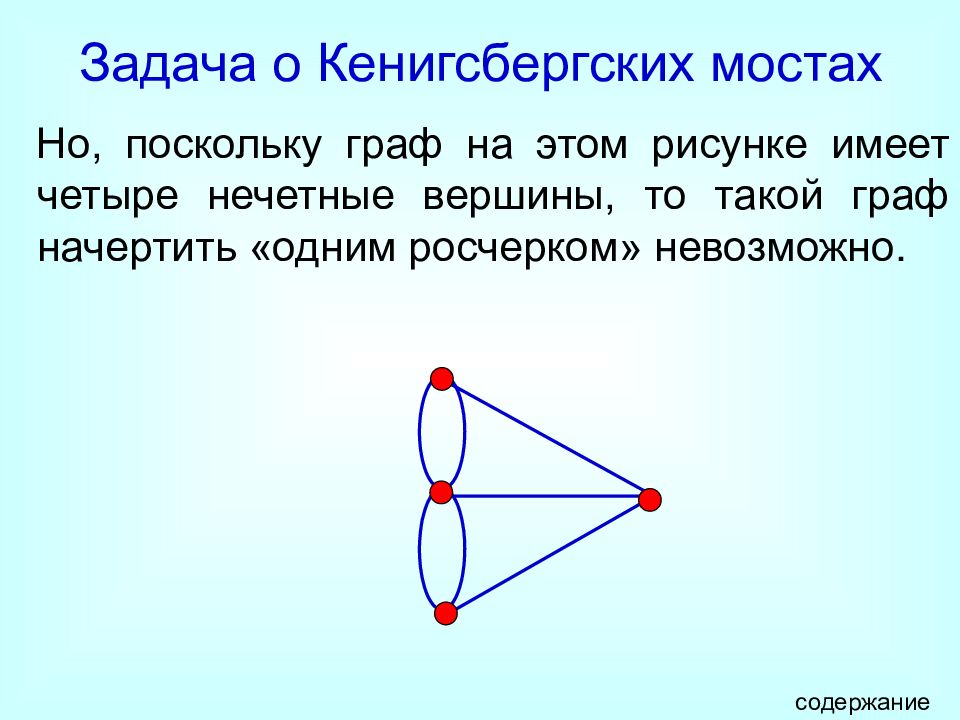
Слайд 7: Задача о Кенигсбергских мостах
Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно. содержание
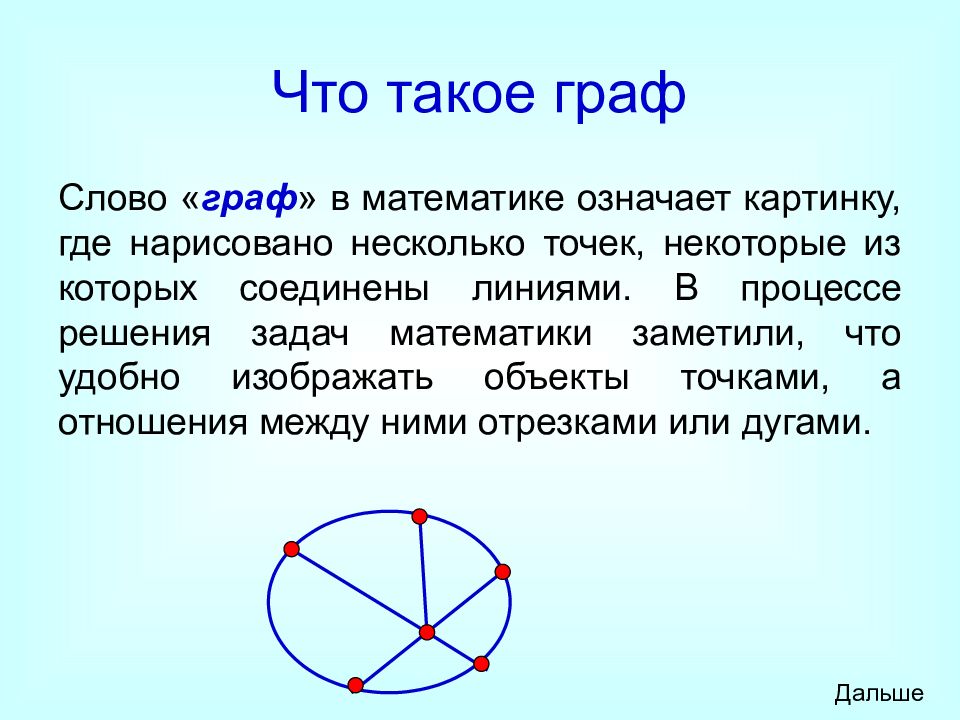
Слайд 8: Что такое граф
Слово « граф » в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. В процессе решения задач математики заметили, что удобно изображать объекты точками, а отношения между ними отрезками или дугами. Дальше
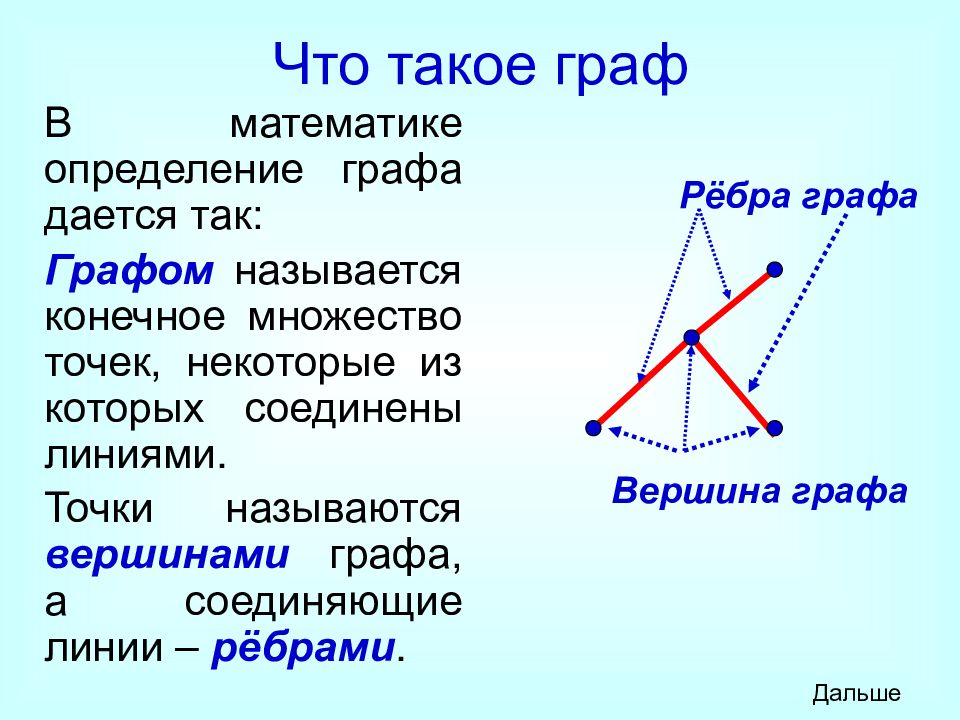
Слайд 9: Что такое граф
В математике определение графа дается так: Графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами. Рёбра графа Вершина графа Дальше
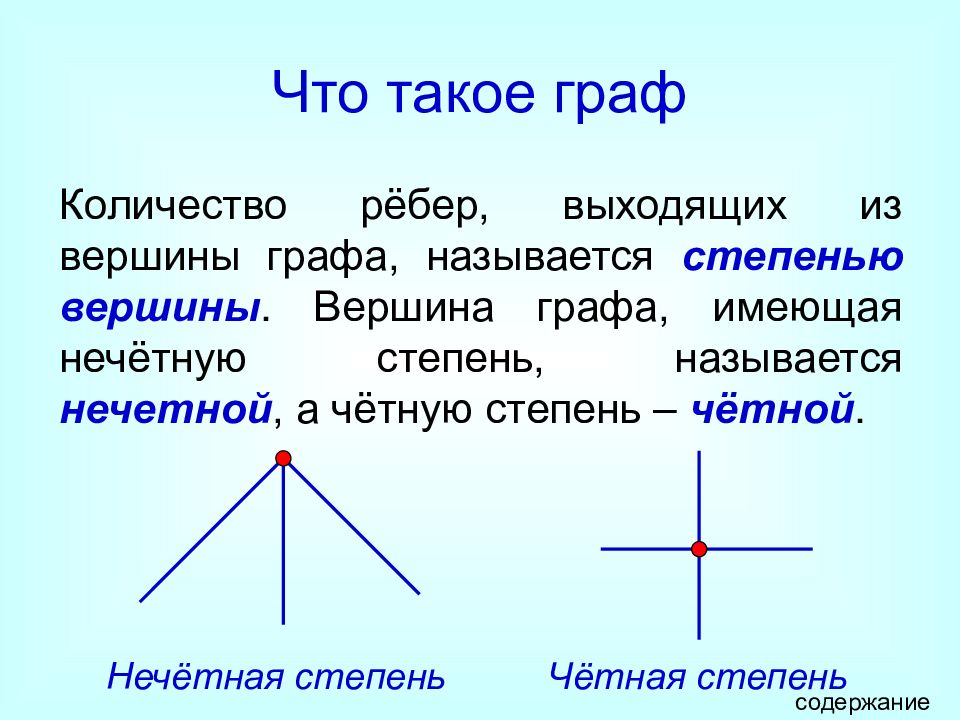
Слайд 11: Что такое граф
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной. Нечётная степень Чётная степень содержание
Слайд 12: Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Решая задачу О кенигсбергских мостах, Эйлер сформулировал свойства графа: Невозможно начертить граф с нечетным числом нечетных вершин. дальше
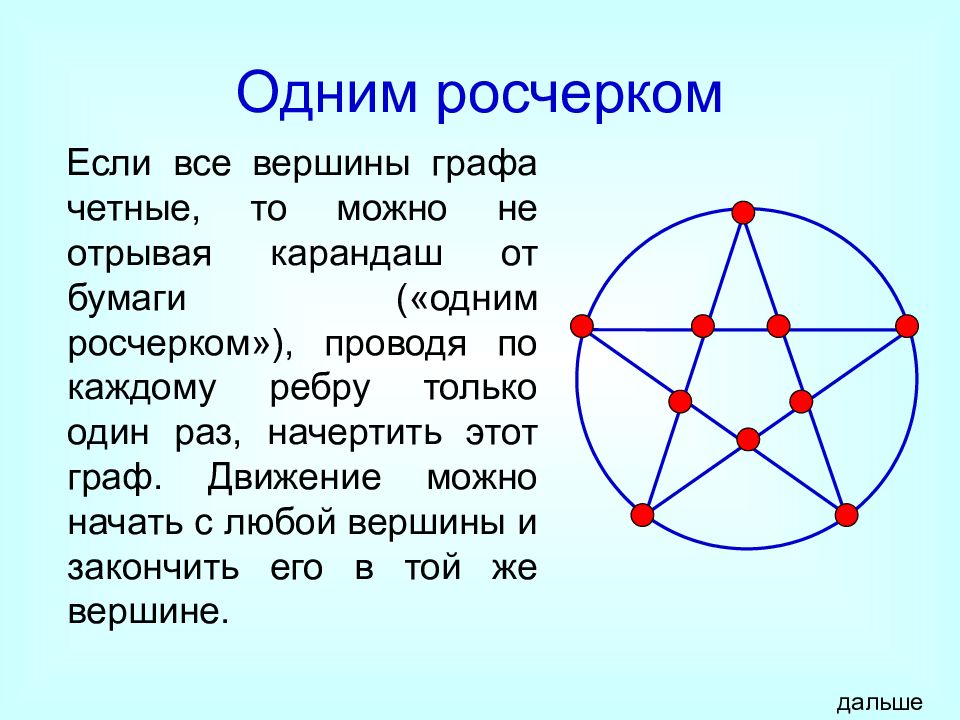
Слайд 13: Одним росчерком
Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине. дальше
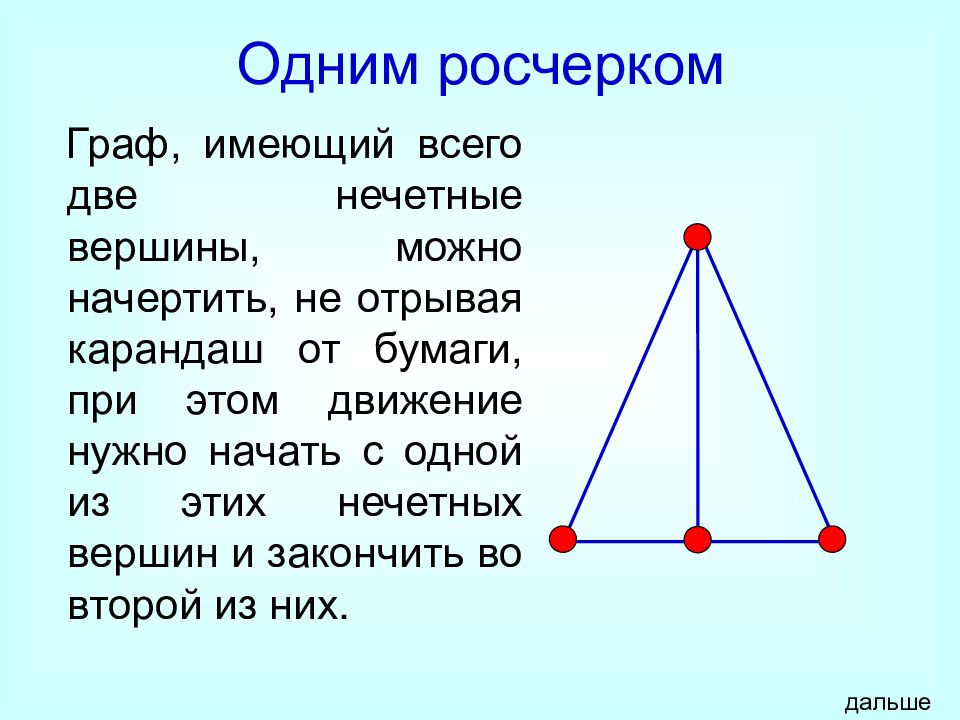
Слайд 14: Одним росчерком
Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них. дальше
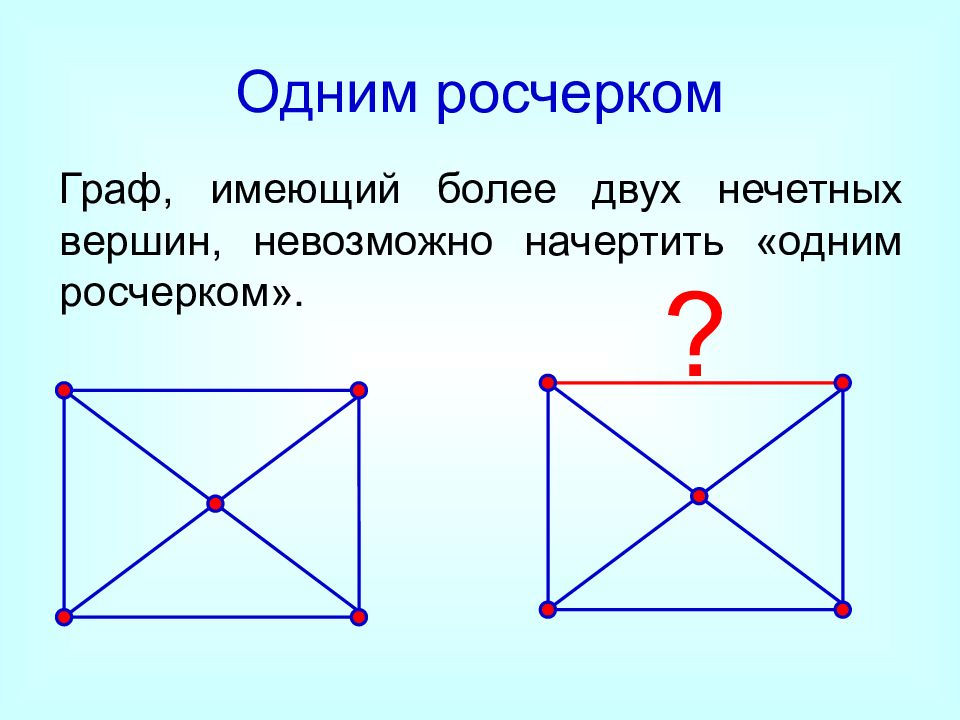
Слайд 15: Одним росчерком
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком». ?
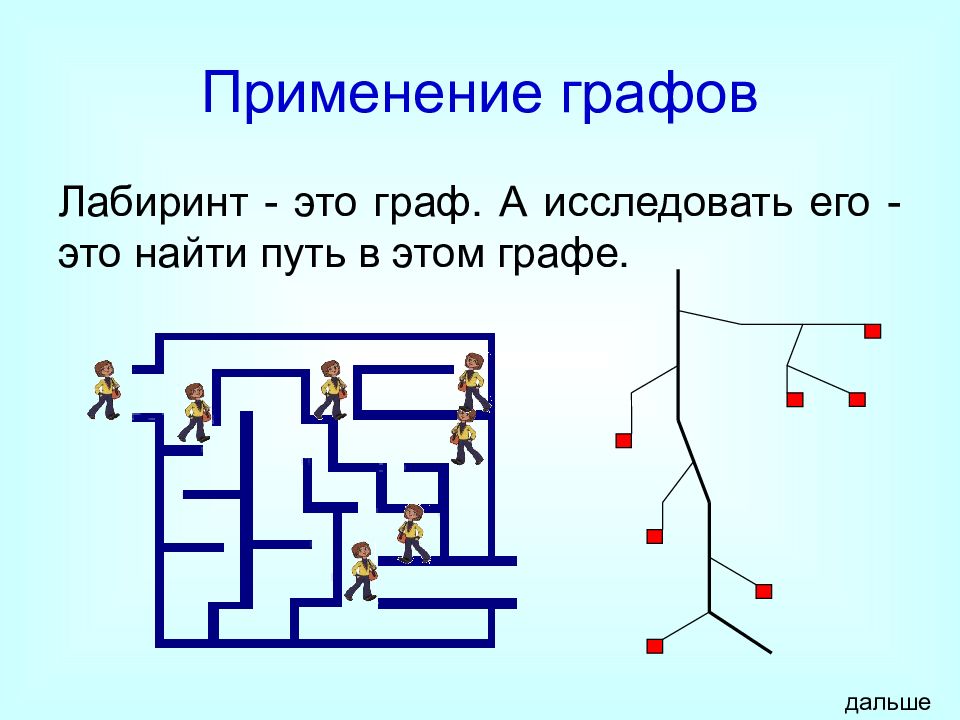
Слайд 17: Применение графов
Лабиринт - это граф. А исследовать его - это найти путь в этом графе. дальше
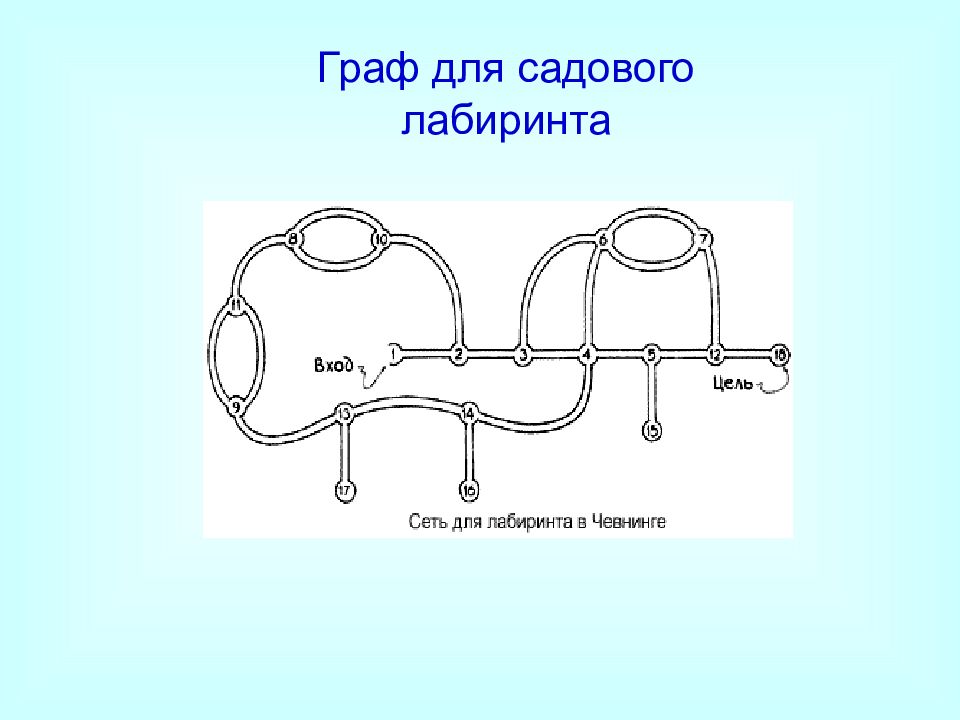
Слайд 19
Первый многосвязный садовый лабиринт был сооружён в 1820-е годы в Чевнинге в Великобритании.
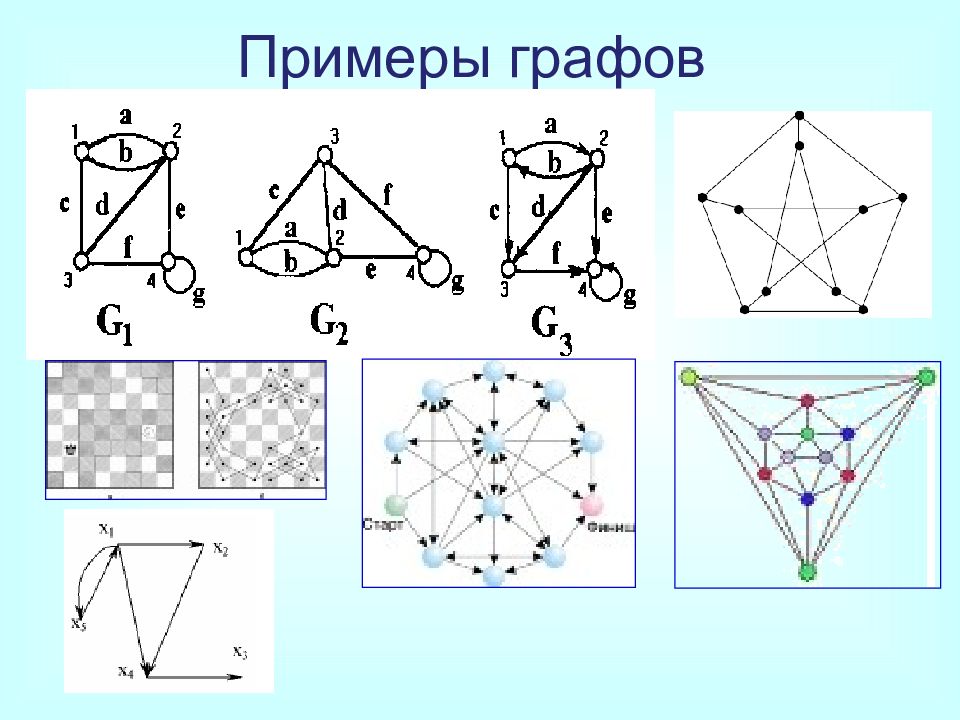
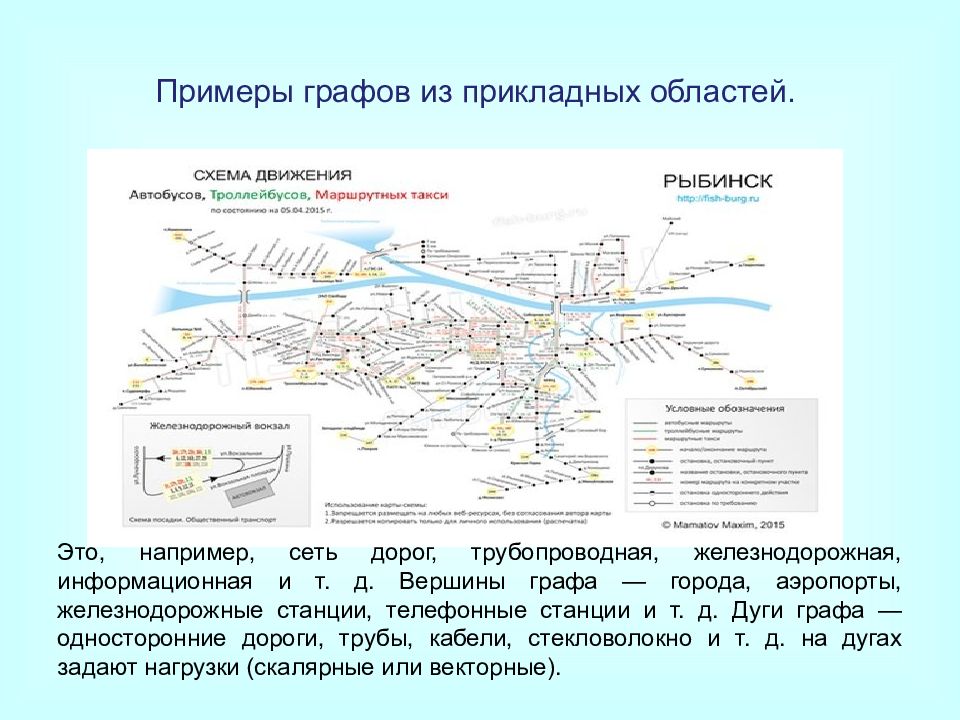
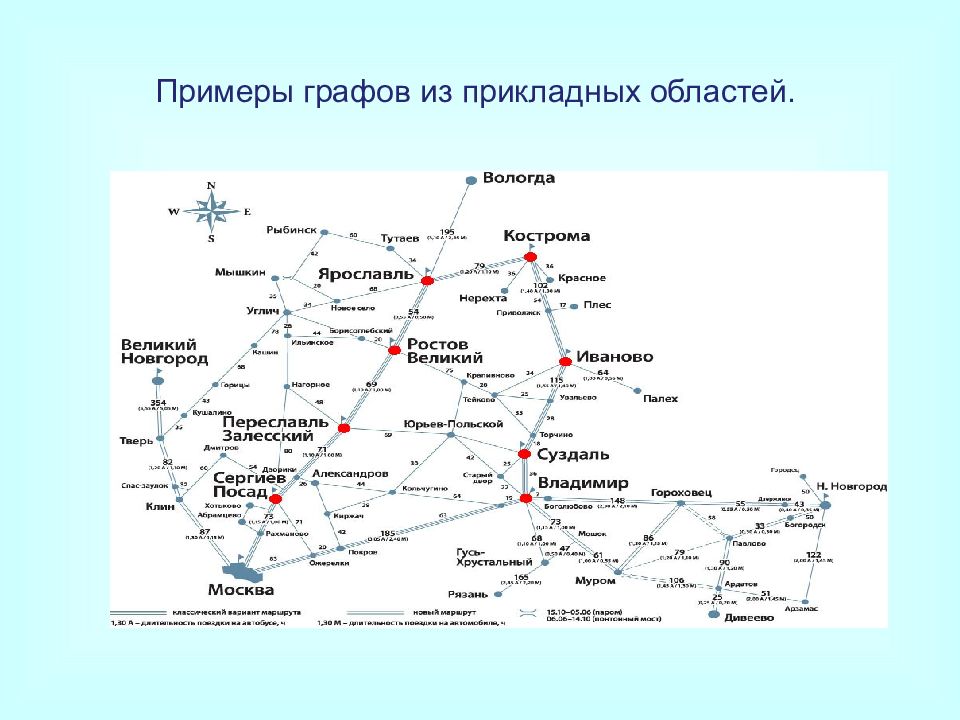
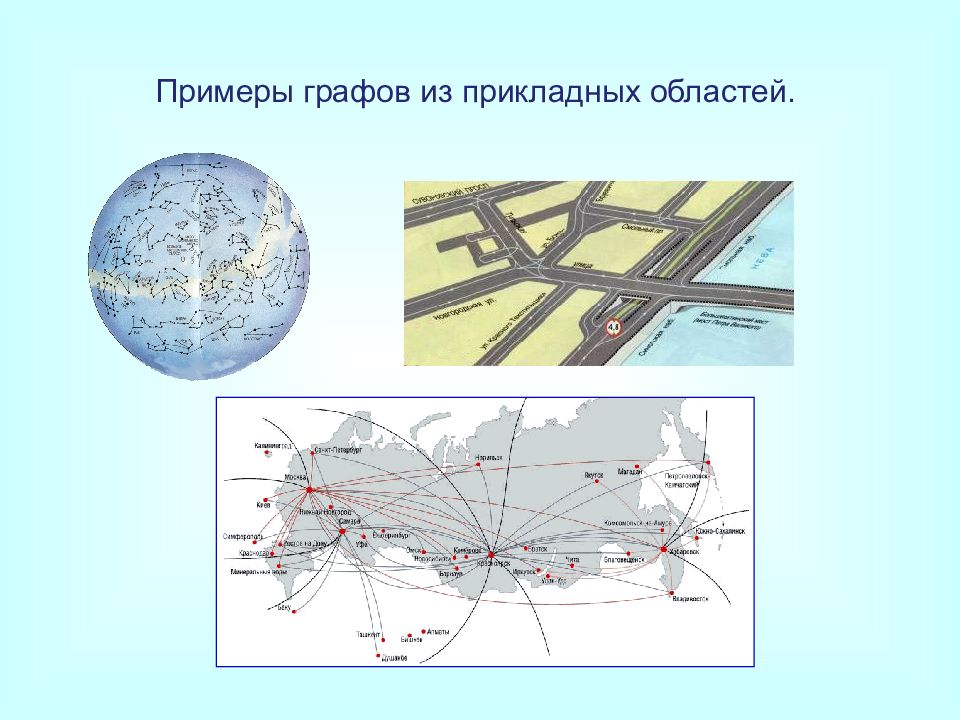
Слайд 22: Примеры графов из прикладных областей
Это, например, сеть дорог, трубопроводная, железнодорожная, информационная и т. д. Вершины графа — города, аэропорты, железнодорожные станции, телефонные станции и т. д. Дуги графа — односторонние дороги, трубы, кабели, стекловолокно и т. д. на дугах задают нагрузки (скалярные или векторные). Примеры графов из прикладных областей.
Слайд 25: Ориентированный граф и неориенти-рованный граф (орграф и н-граф)
Существуют два основных вида графов: ориентированные и неориентированные. Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным (орграф). Ребра ориентированного графа называются дугами. Соответствующие вершины ориентированного графа называют началом и концом. Если направления ребер не указываются, то граф называется неориентированным или просто графом ( н-граф ). Ориентированный граф и неориенти-рованный граф (орграф и н-граф)
Слайд 26: Примеры орграфа и н-графа
Пример 1. Неориентированный граф G = (X, E). X = {x1, x2, x3, x4}, E = {a1(x1, x2), a2(x2, x3), a3(x1, x3), a4(x3, x4)}. Пример 2. Ориентированный граф G = (X, A). X = {x1, x2, x3, x4}, A = {a1(x1, x2), a2 (x1, x3),a3 ( x3, x4), a4 (x3, x2)}.
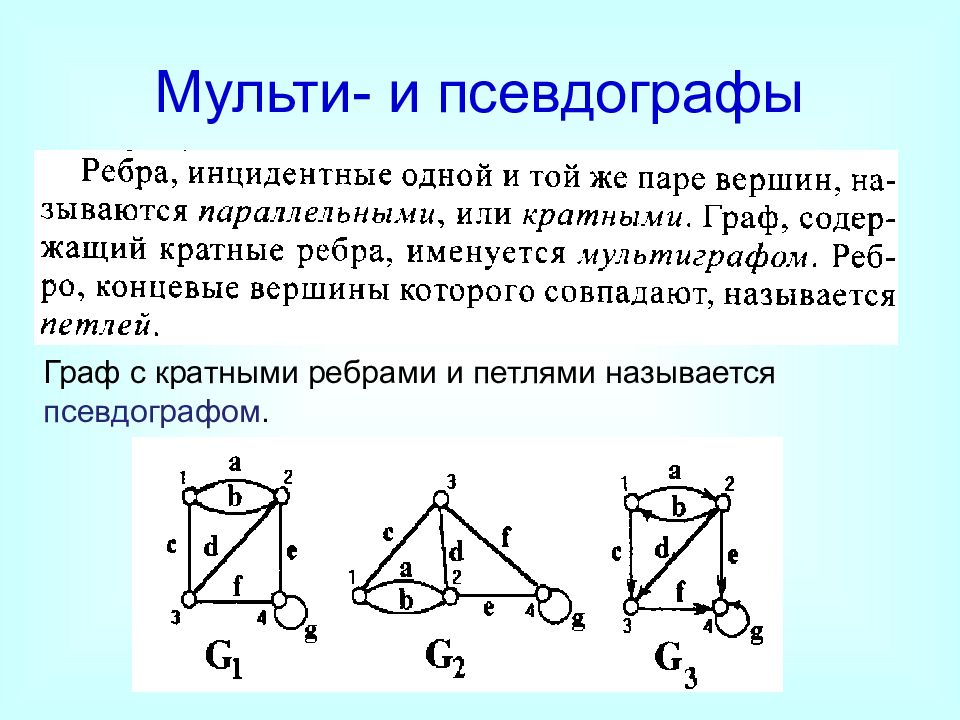
Слайд 27: Мульти- и псевдографы
Граф с кратными ребрами и петлями называется псевдографом. Мульти- и псевдографы
Слайд 28
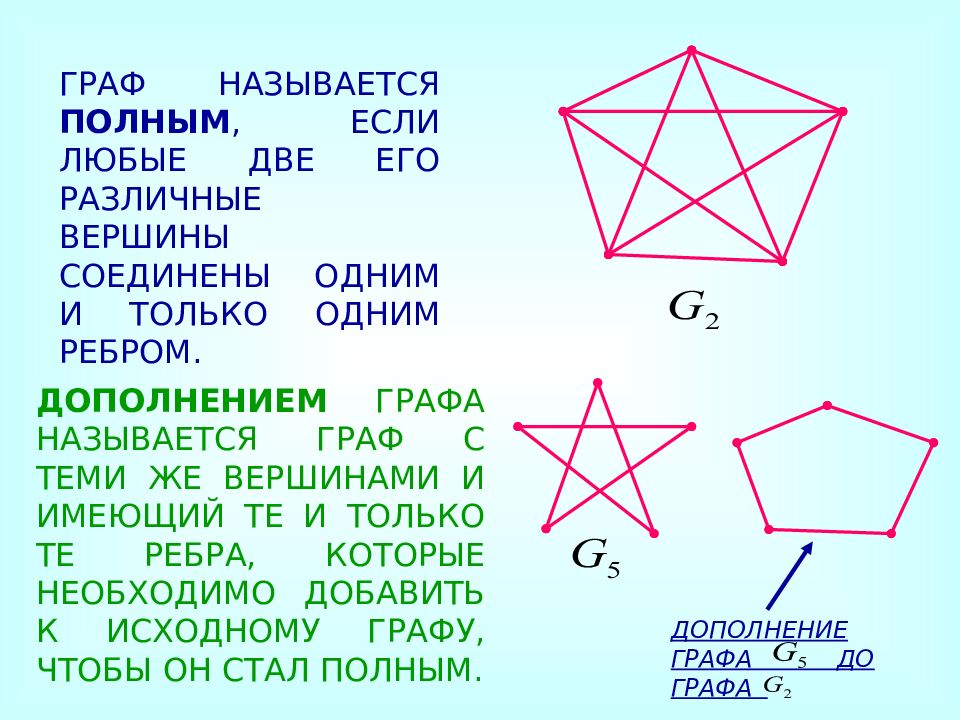
ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ. ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ. ДОПОЛНЕНИЕ ГРАФА ДО ГРАФА
Слайд 29: Смежные вершины и ребра
Две вершины называются смежными, если они инцидентны одному и тому же ребру. Два ребра называются смежными, если они имеют общую вершину Смежные вершины и ребра
Слайд 30: Степень вершины в н-графе
Степенью вершины н-графа называется число ребер, инцидентных этой вершине. Вершина, имеющая степень 0, называется изолированной, а степень 1 – висячей. Степень вершины в н-графе Граф, состоящий из изолированных вершин называется нуль-графом. В н-графе сумма степеней всех вершин равна удвоенному числу ребер m графа (в графе с петлями петля дает вклад 2 в степень вершины): deg v i = 2m
Слайд 31
ТЕОРЕМА В ГРАФЕ СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА: ТЕОРЕМА ЧИСЛО НЕЧЕТНЫХ ВЕРШИН ЛЮБОГО ГРАФА – ЧЕТНО. СЛЕДСТВИЕ ЧИСЛО ВЕРШИН МНОГОГРАННИКА, В КОТОРЫХ СХОДИТСЯ НЕЧЁТНОЕ ЧИСЛО РЁБЕР, ЧЁТНО. Степень А +степень В + степень С +…= 2*число рёбер НЕЧЁТНОЕ ЧИСЛО ЗНАКОМЫХ В ЛЮБОЙ КОМПАНИИ ВСЕГДА ЧЁТНО.
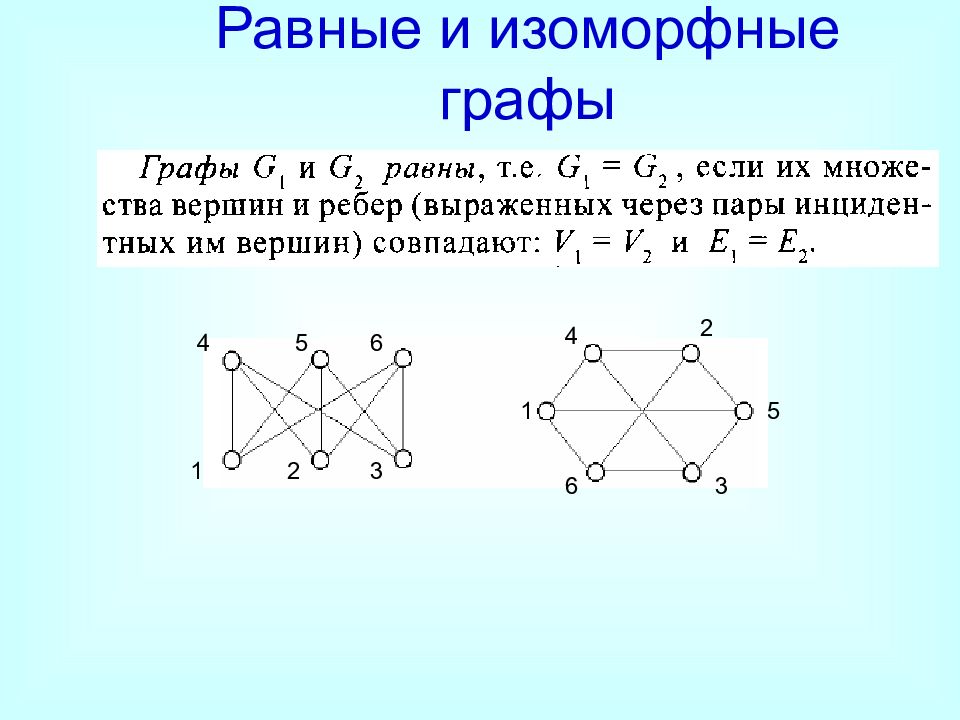
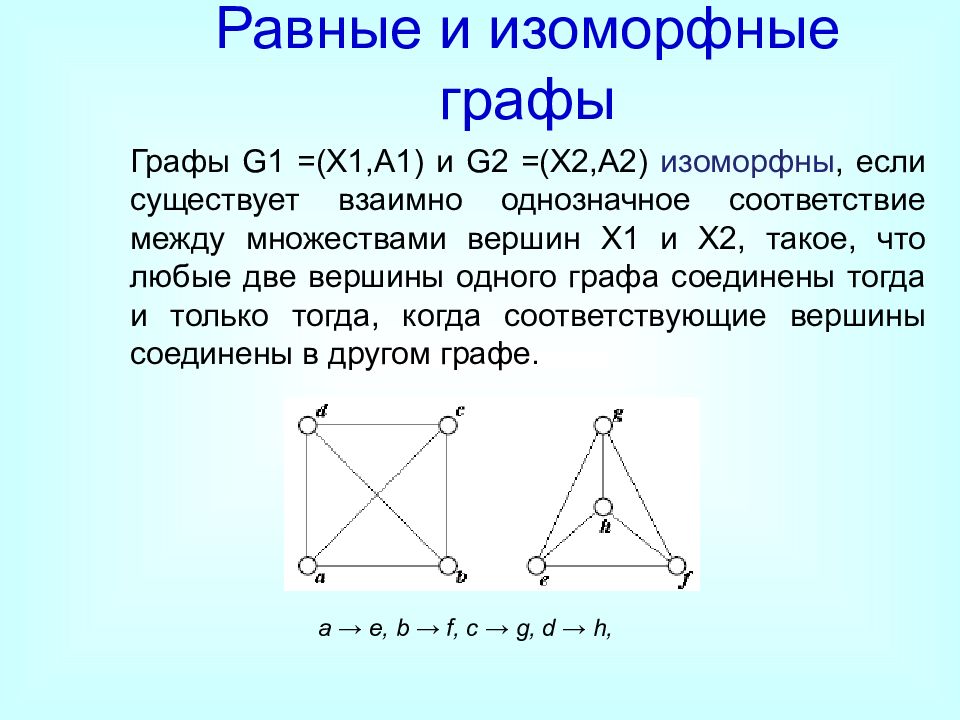
Слайд 33: Равные и изоморфные графы
Графы G1 =(X1,A1) и G2 =(X2,A2) изоморфны, если существует взаимно однозначное соответствие между множествами вершин X1 и X2, такое, что любые две вершины одного графа соединены тогда и только тогда, когда соответствующие вершины соединены в другом графе. Равные и изоморфные графы a → e, b → f, c → g, d → h,
Слайд 34: Планарные графы
Граф G = (X, A) – планарный, если он может быть изображен на плоскости так, что не будет пересекающихся дуг. Планарные графы Граф G ’(V’, E’) называется подграфом G (V, E), если V’ ⊂ V, ’ E’ ⊂ E. Обозначается G’ ⊂ G.
Слайд 36
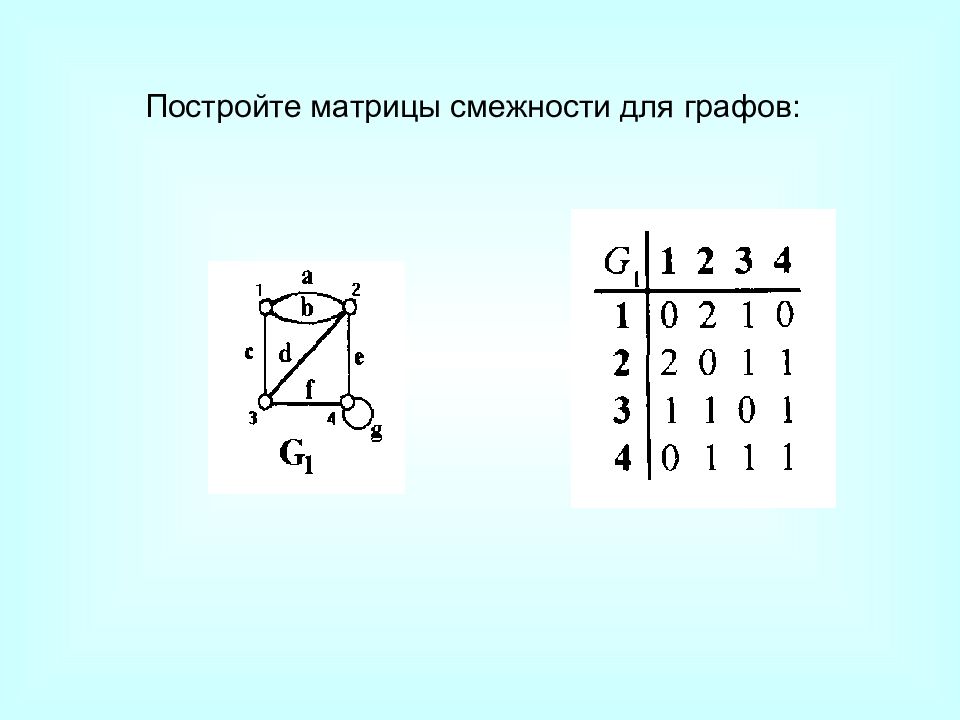
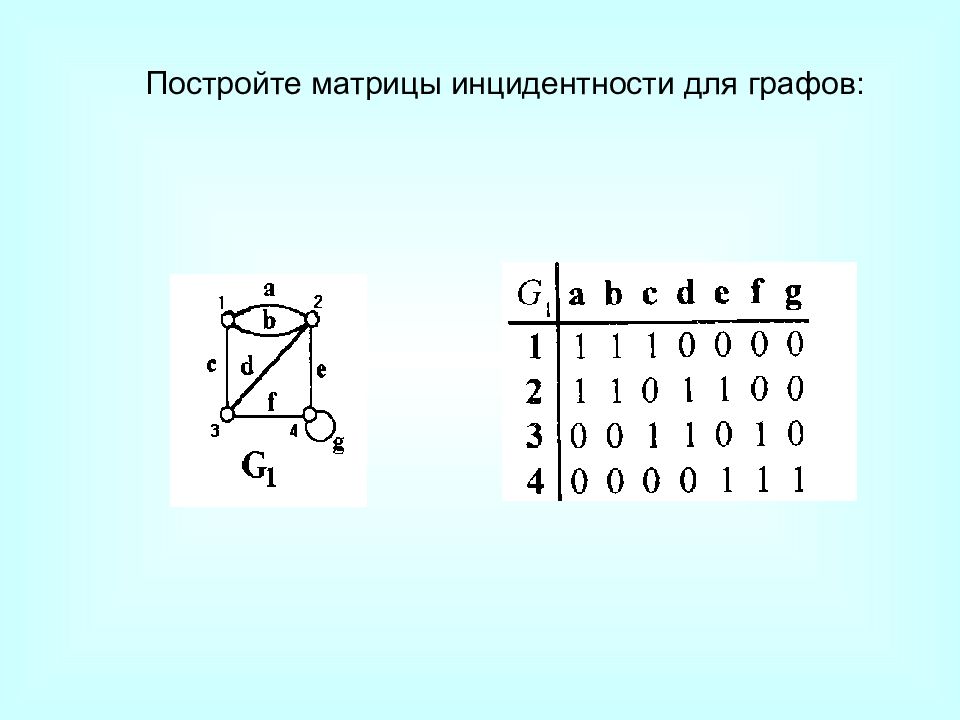
Возможны следующие различные способы задания графа: посредством графического изображения; указанием множества вершин и множества ребер (дуг); матрицей смежности; матрицей инцидентности. Способы задания графов
Слайд 37
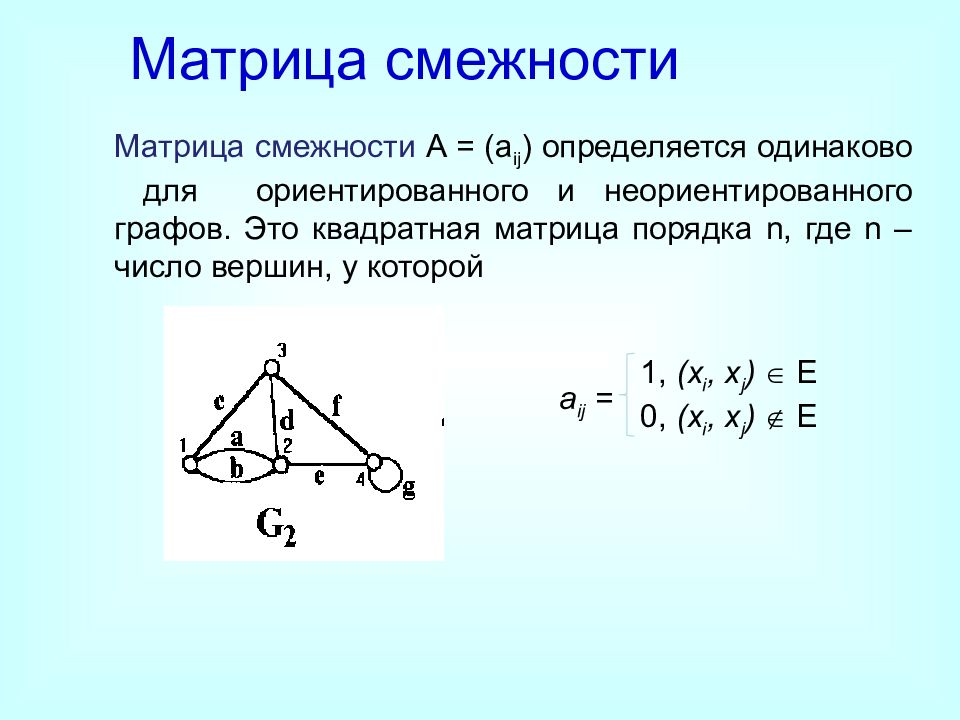
Матрица смежности A = ( a ij ) определяется одинаково для ориентированного и неориентированного графов. Это квадратная матрица порядка n, где n – число вершин, у которой Матрица смежности a ij = 1, (x i, x j ) E 0, (x i, x j ) E
Слайд 39
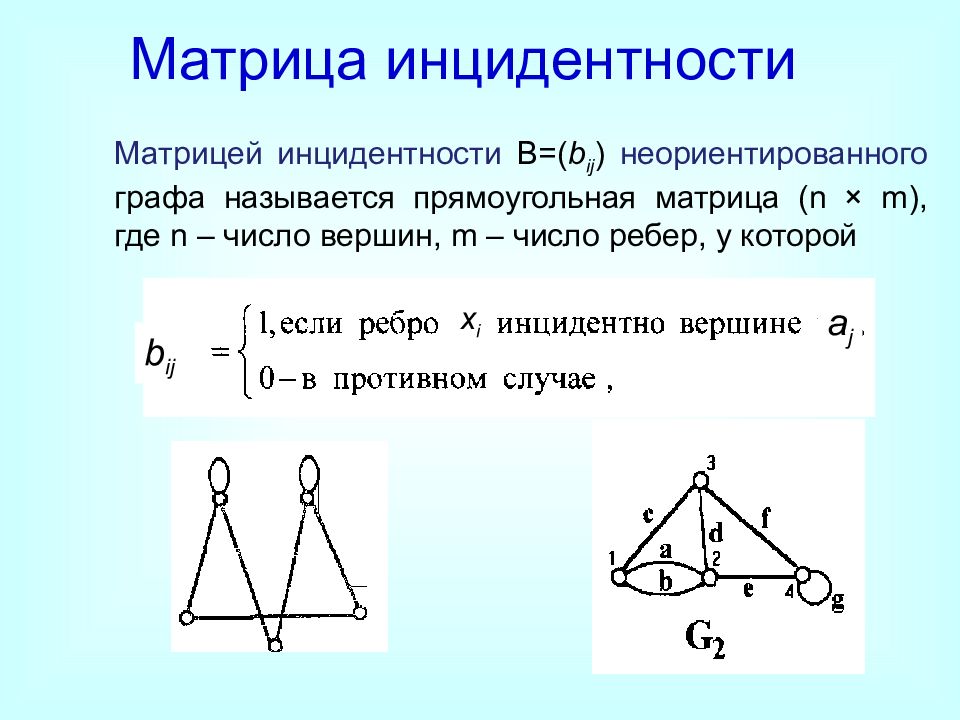
Матрица инцидентности Матрицей инцидентности B=( b ij ) неориентированного графа называется прямоугольная матрица ( n × m ), где n – число вершин, m – число ребер, у которой x i a j b ij
Слайд 41: Выводы
Графы – это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические задачи. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы используются при составлении карт и генеалогических древ. В математике даже есть специальный раздел, который так и называется: « Теория графов ». содержание
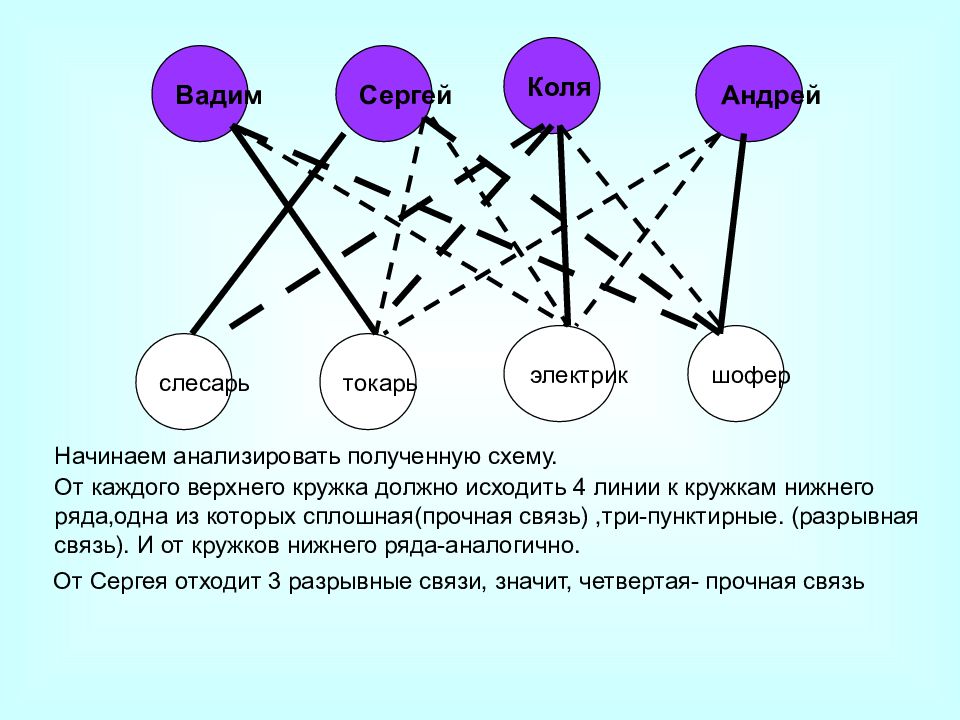
Слайд 43: Условие задачи
В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, Электрик-младший из друзей. По вечерам Андрей и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей. Условие задачи
Слайд 44
Вадим Коля Сергей Андрей слесарь токарь электрик шофер Начинаем анализировать полученную схему. От каждого верхнего кружка должно исходить 4 линии к кружкам нижнего ряда,одна из которых сплошная(прочная связь), три-пунктирные. (разрывная связь). И от кружков нижнего ряда-аналогично. От Сергея отходит 3 разрывные связи, значит, четвертая- прочная связь
Последний слайд презентации: История
Андрей, Борис, Володя, Даша, Галя договорились созвониться по телефону о посещении кино. Вечером у кинотеатра собрались не все. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша – Андрею и Володе, а Галя – Андрею, Володе и Борису. Кто не пришёл в кино, если все они условились, что поход в кино состоится только в том случае, если созвонятся все? Задача.