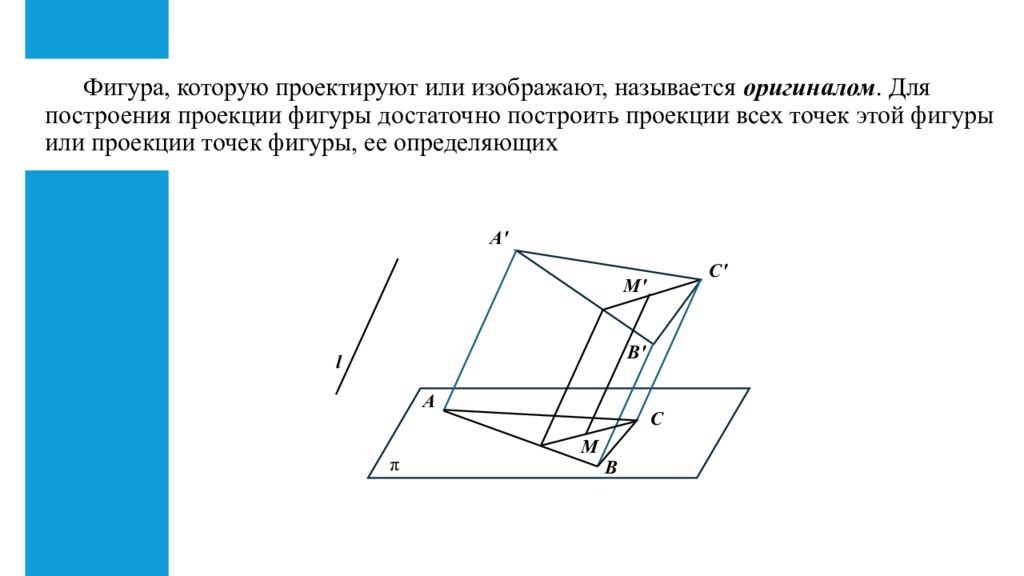
Слайд 2: Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, ее определяющих
π l A ' C ' B ' M ' A В С М Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, ее определяющих
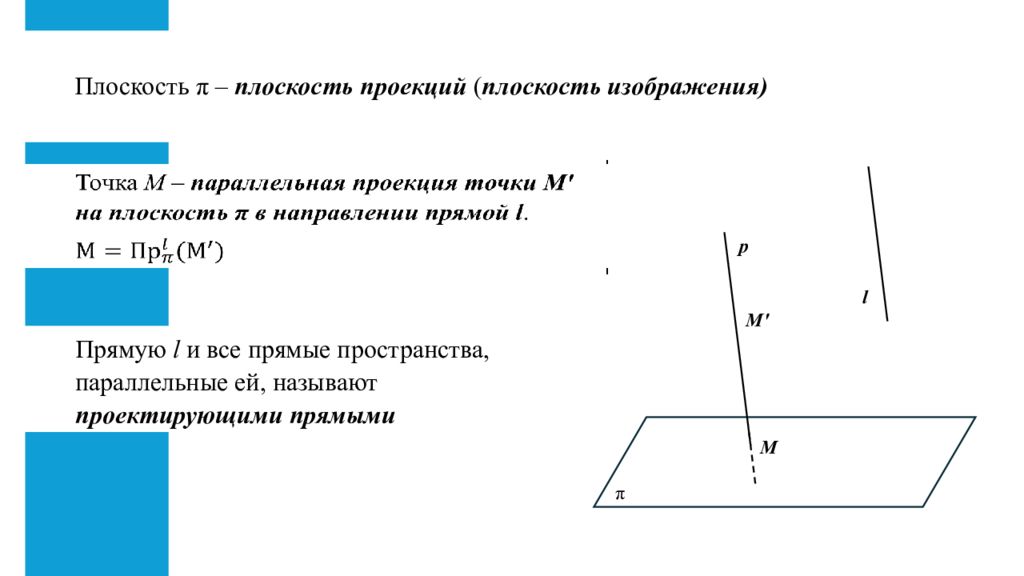
Слайд 3: Плоскость π – плоскость проекций ( плоскость изображения)
π l M ' M p Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми
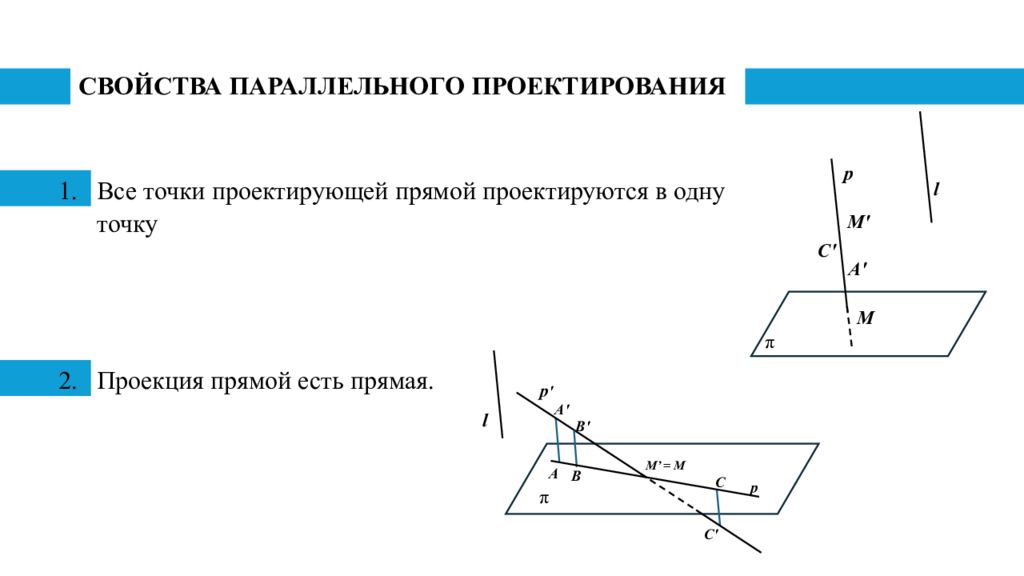
Слайд 5: СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ
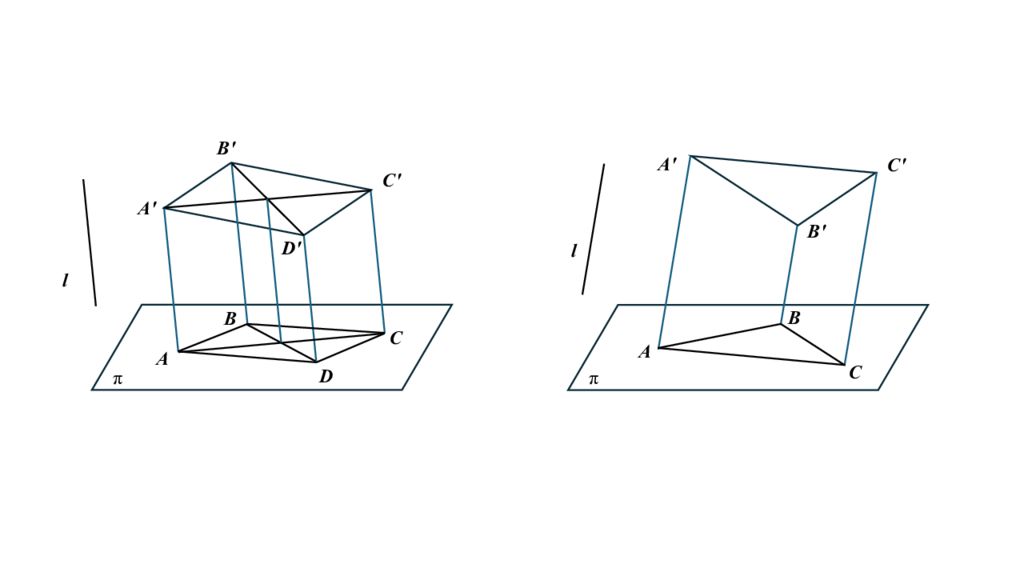
Все точки проектирующей прямой проектируются в одну точку Проекция прямой есть прямая. π l M ' M p A ' C ' π l p ' A ' В' М’ = М A В С С ' p
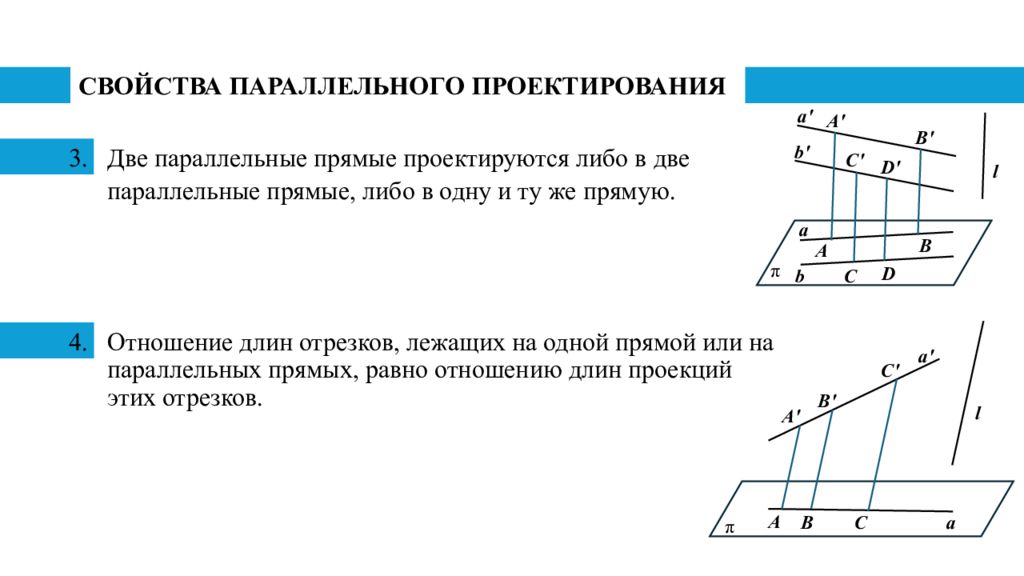
Слайд 6: СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ
В D C А СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков. π l А' В' С' D ' a ' b ' a b π l a С' A ' B ' a ' A B C
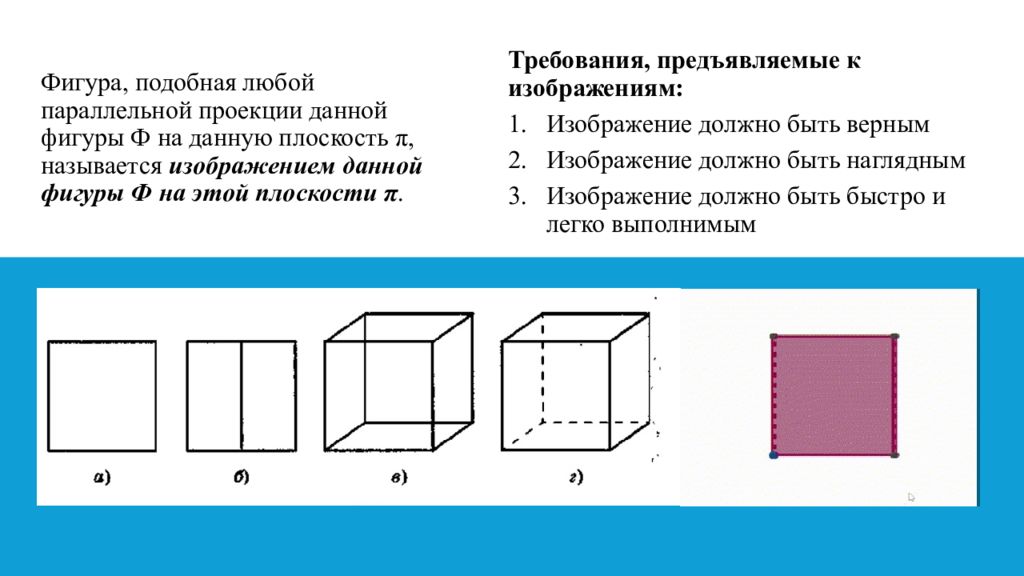
Слайд 7: Фигура, подобная любой параллельной проекции данной фигуры Ф на данную плоскость π, называется изображением данной фигуры Ф на этой плоскости π
Требования, предъявляемые к изображениям : Изображение должно быть верным Изображение должно быть наглядным Изображение должно быть быстро и легко выполнимым
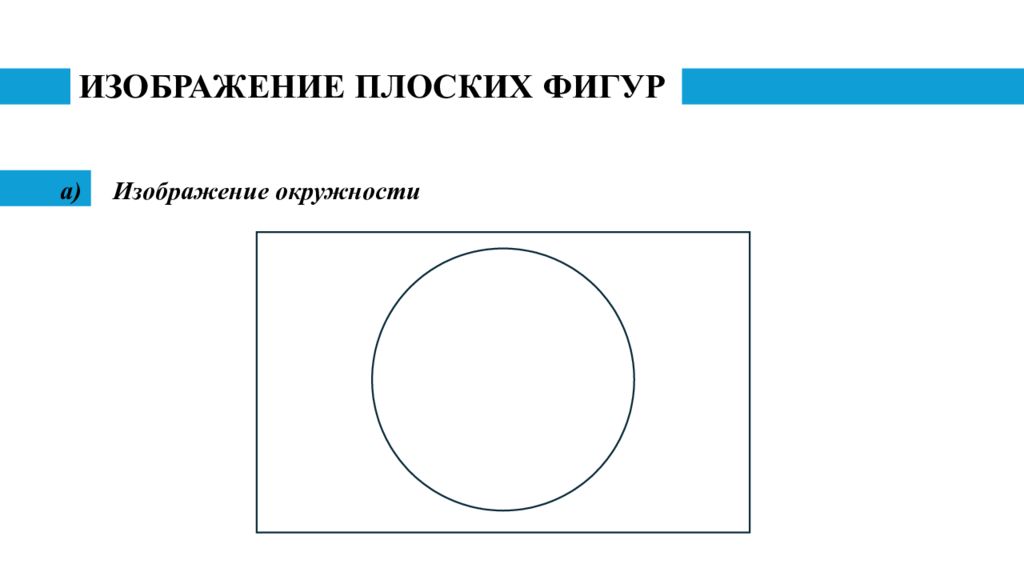
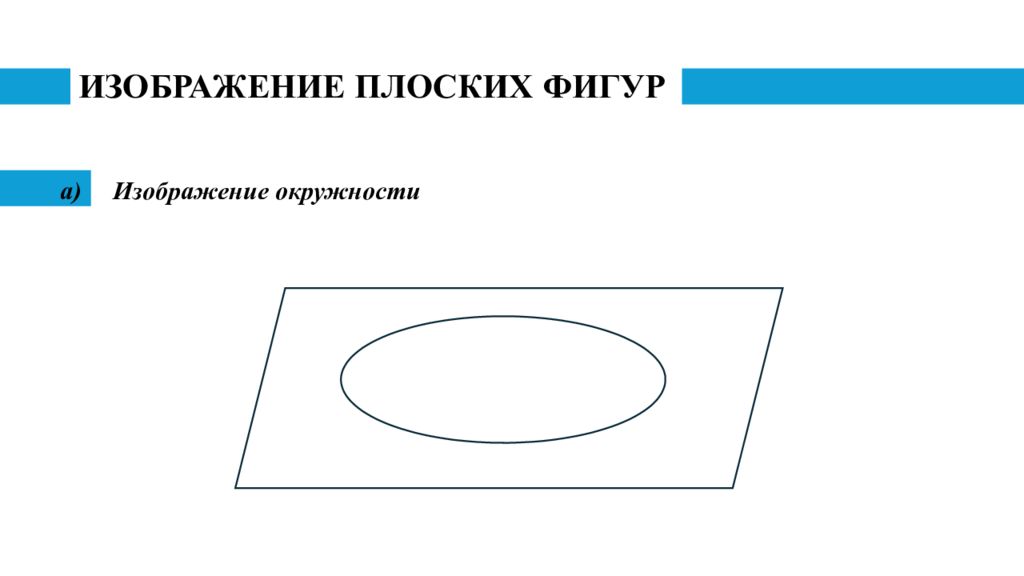
Слайд 11: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Изображение треугольника Теорема 1 (теорема об изображении треугольника). Любой треугольник АВС может служить изображением любого треугольника А'B'С'.
Слайд 12: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Изображение треугольника Теорема 2. Если на плоскости изображения π треугольник АВС служит изображением треугольника А'B'C', то на плоскости π однозначно строится изображение любой точки плоскости α = (А'B’С').
Слайд 13: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Алгоритм построения изображения плоской фигуры таков: 1. Начертить оригинал (с точностью до подобия). 2. Выделить в оригинале какой-либо треугольник. 3. Изобразить этот треугольник произвольным треугольником. 4. Постепенно строить изображения остальных точек (элементов) оригинала, используя лишь его аффинные свойства.
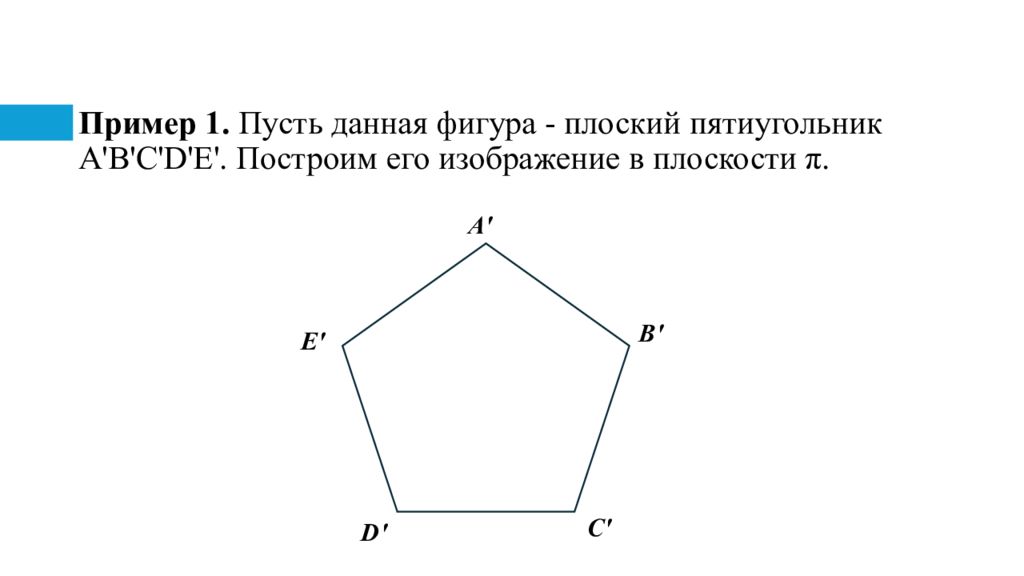
Слайд 14: Пример 1. Пусть данная фигура - плоский пятиугольник A'B'C'D'E'. Построим его изображение в плоскости π
A' B ' C ' D ' E '
Слайд 15
ЗАДАЧА 1. Треугольник АВС является изображением правильного треугольника А'B'С'. Постройте изображение центра окружности, описанной около треугольника A'B'С’. ЗАДАЧА 2. Дано изображение окружности c центром О' и вписанного в нее треугольника А'В'С'. Постройте изображение точки Н' пересечения высот этого треугольника
Слайд 16: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Изображение параллелограмма и трапеции Изображением параллелограмма на основании свойств параллельного проектирования является параллелограмм.
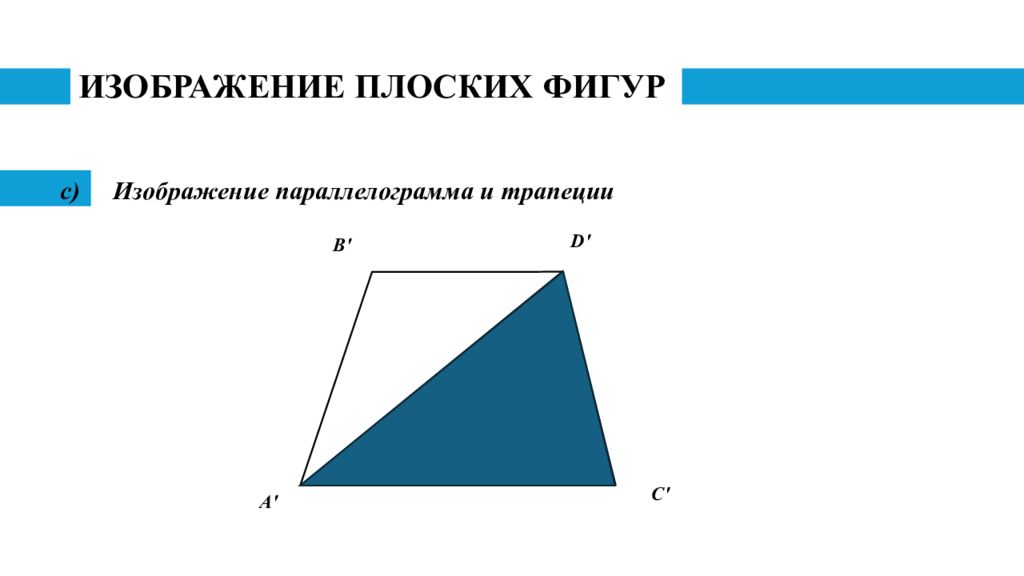
Слайд 17: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Изображение параллелограмма и трапеции A ' B ' C ' D '
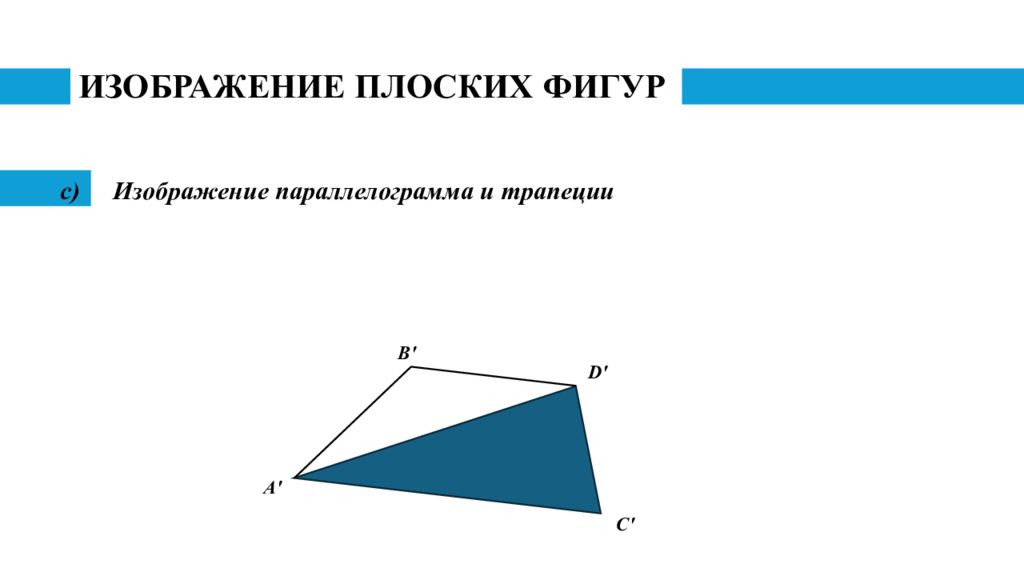
Слайд 18: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Изображение параллелограмма и трапеции A ' C ' D ' B '
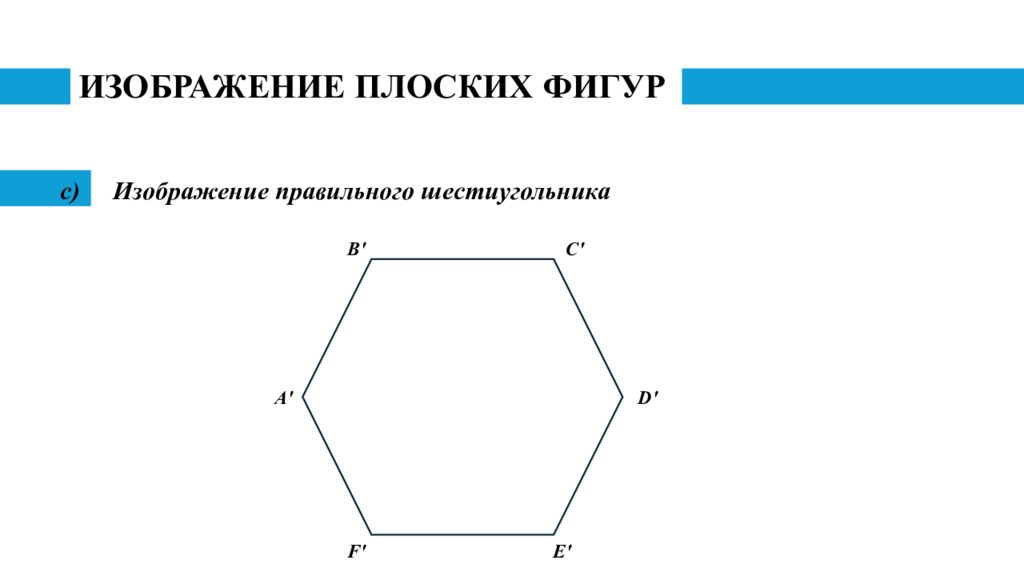
Слайд 19: ИЗОБРАЖЕНИЕ ПЛОСКИХ ФИГУР
Изображение правильного шестиугольника B ' D ' А' E ' F ' C '