Слайд 2: ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ
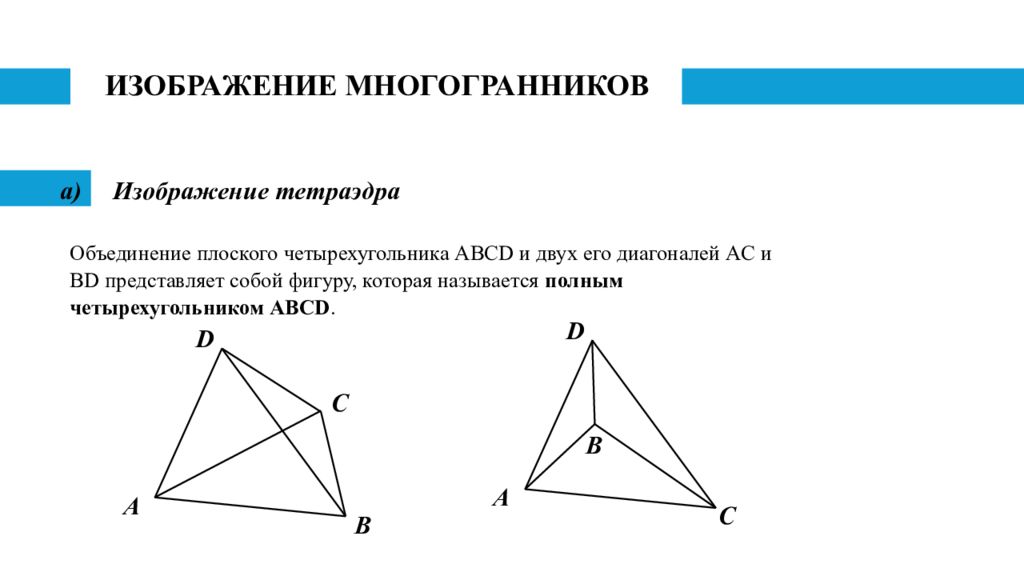
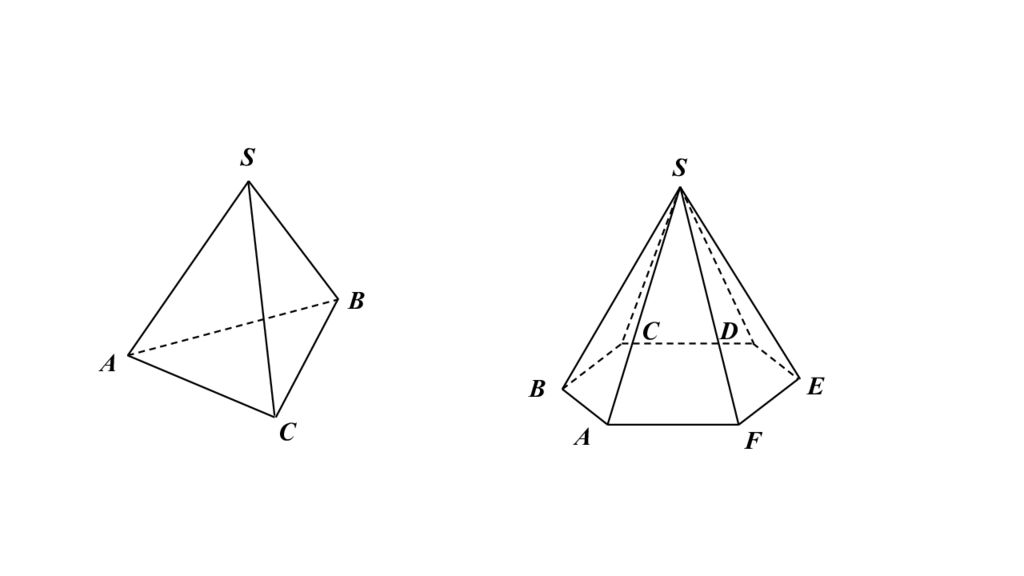
Изображение тетраэдра Объединение плоского четырехугольника ABCD и двух его диагоналей AC и BD представляет собой фигуру, которая называется полным четырехугольником ABCD. A B C D A B C D
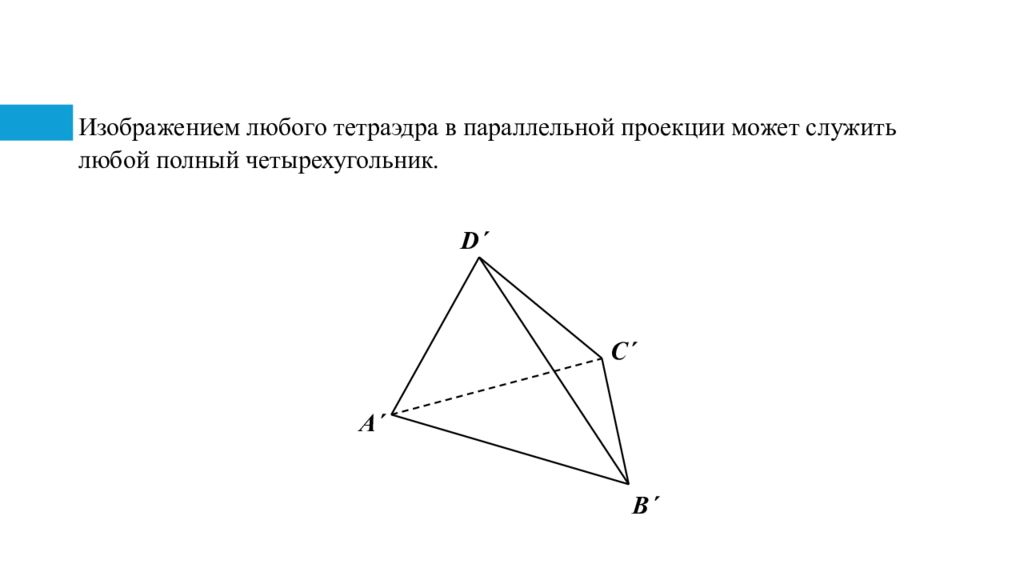
Слайд 3: Изображением любого тетраэдра в параллельной проекции может служить любой полный четырехугольник
A΄ B ΄ C ΄ D ΄
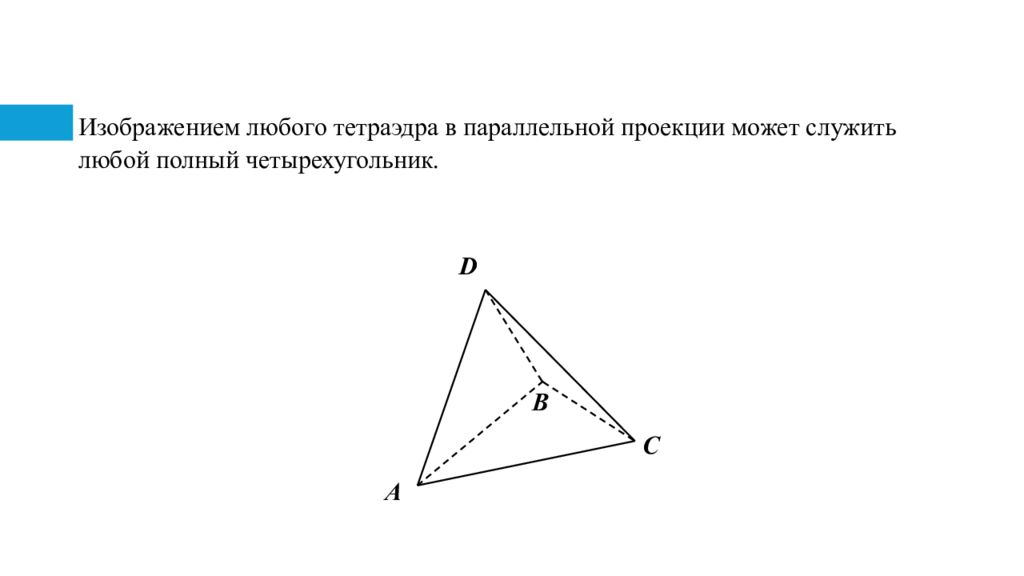
Слайд 4: Изображением любого тетраэдра в параллельной проекции может служить любой полный четырехугольник
A B C D
Слайд 5: ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ
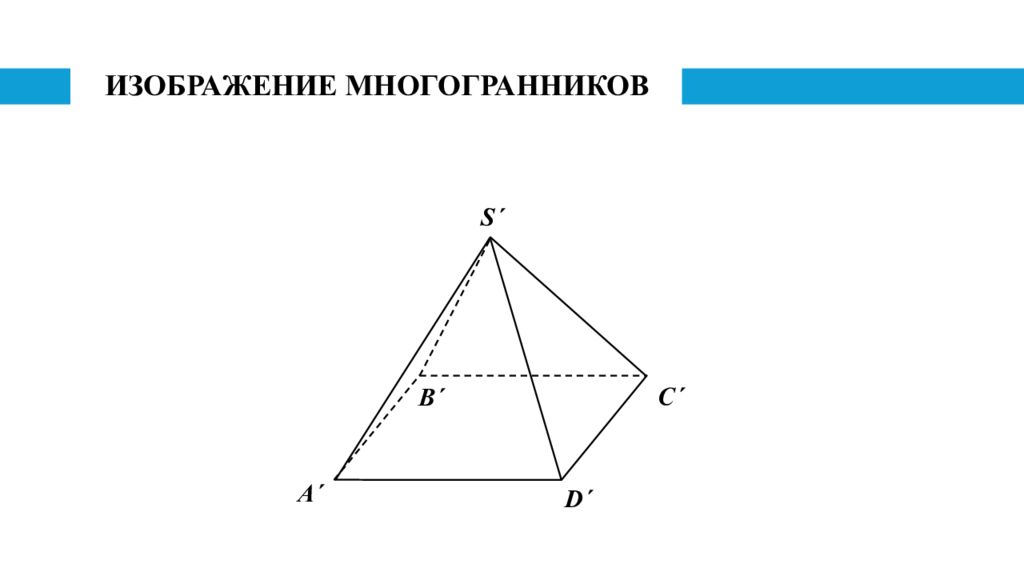
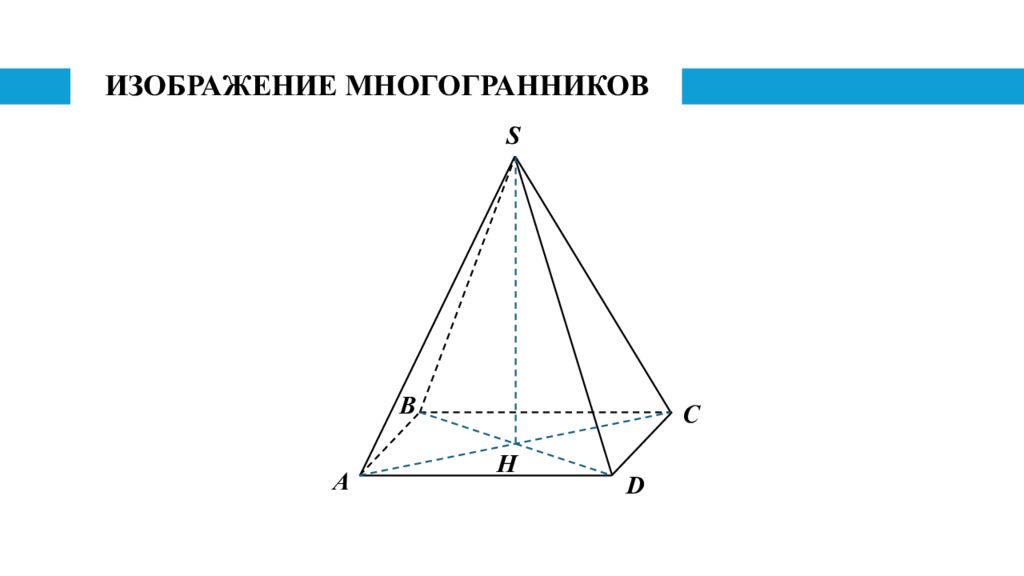
Изображение пирамиды Для построения верного и наглядного изображения правильной пирамиды сначала строят изображение основания этой пирамиды и его центра. Затем из этого центра вертикально вверх проводят луч, на котором отмечают произвольную точку и принимают ее в качестве вершины искомого изображения данной пирамиды, а отрезок, соединяющий эту вершину с точкой, изображающей центр основания, - в качестве изображения высоты данной правильной пирамиды-оригинала.
Слайд 11: ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ
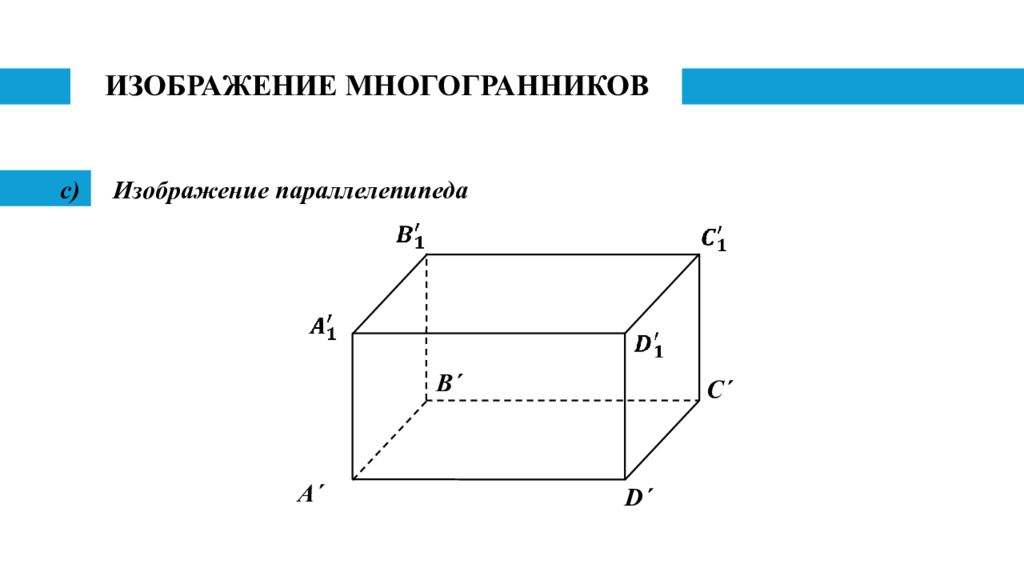
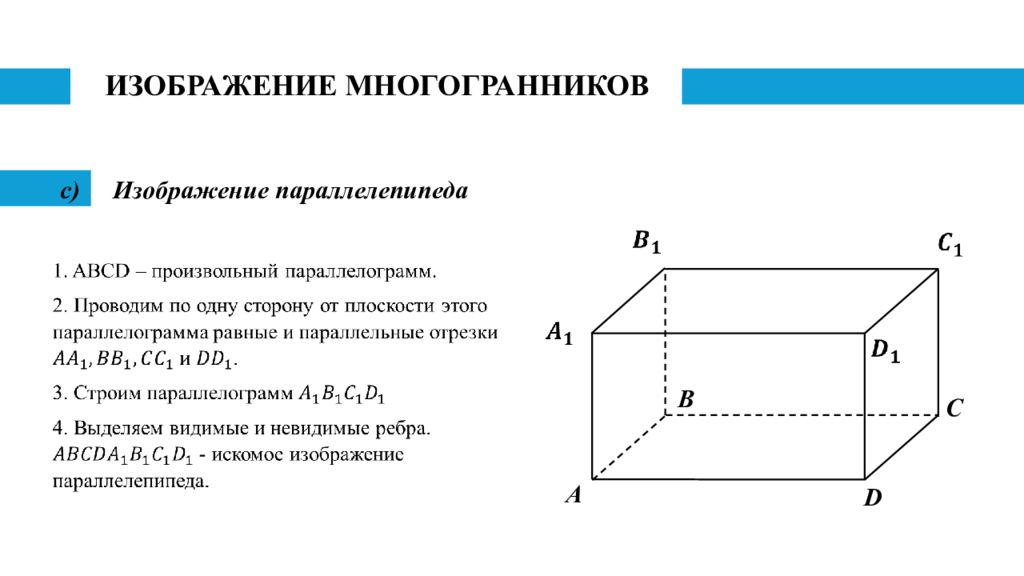
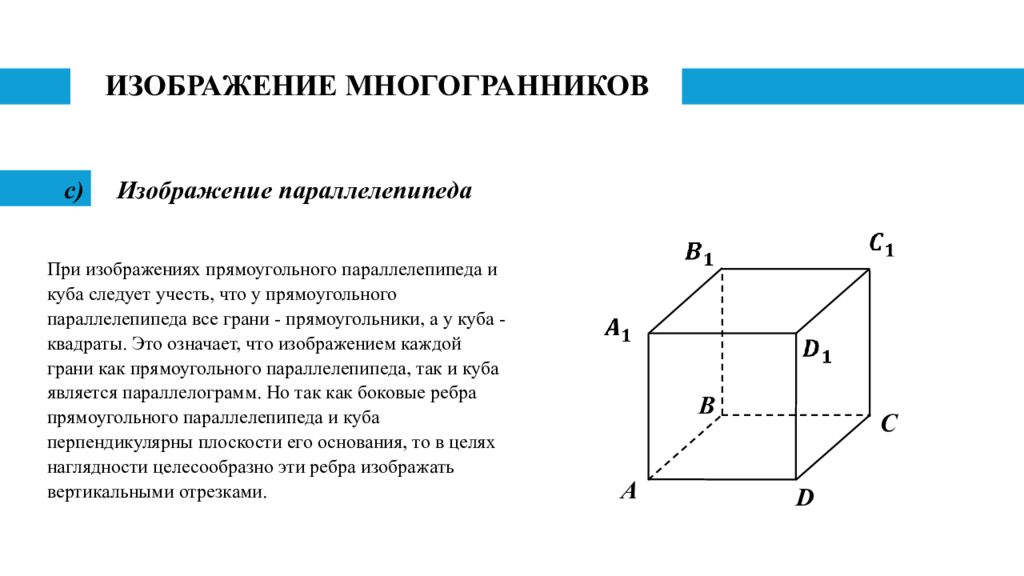
Изображение параллелепипеда B C D A При изображениях прямоугольного параллелепипеда и куба следует учесть, что у прямоугольного параллелепипеда все грани - прямоугольники, а у куба - квадраты. Это означает, что изображением каждой грани как прямоугольного параллелепипеда, так и куба является параллелограмм. Но так как боковые ребра прямоугольного параллелепипеда и куба перпендикулярны плоскости его основания, то в целях наглядности целесообразно эти ребра изображать вертикальными отрезками.
Слайд 12: ИЗОБРАЖЕНИЕ МНОГОГРАННИКОВ
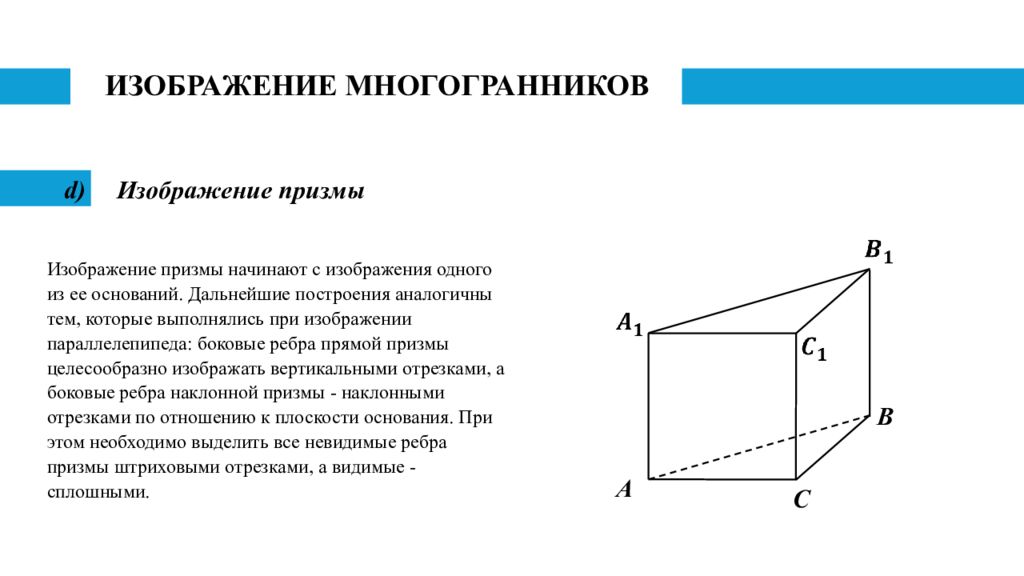
Изображение призмы B C A Изображение призмы начинают с изображения одного из ее оснований. Дальнейшие построения аналогичны тем, которые выполнялись при изображении параллелепипеда: боковые ребра прямой призмы целесообразно изображать вертикальными отрезками, а боковые ребра наклонной призмы - наклонными отрезками по отношению к плоскости основания. При этом необходимо выделить все невидимые ребра призмы штриховыми отрезками, а видимые - сплошными.