8 класс свойство медиан треугольника
Повторение : Определение средней линии треугольника. 1. Теорема о средней линии треугольника. 2. Определение средней линии трапеции. 3. 4. Теорема о средней линии трапеции. 5. Теорема о пропорциональных отрезках.
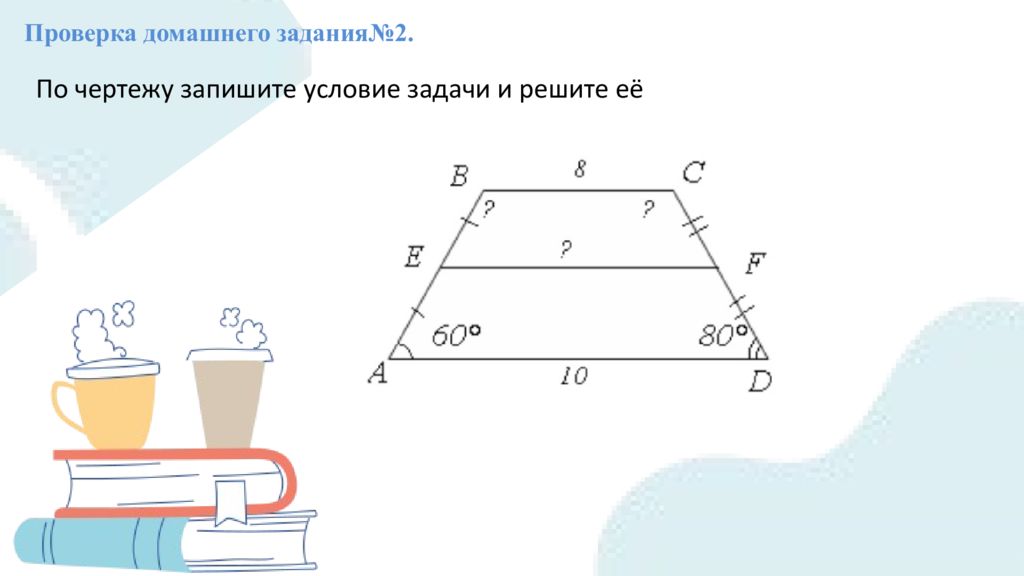
Проверка домашнего задания№ 2. По чертежу запишите условие задачи и решите её
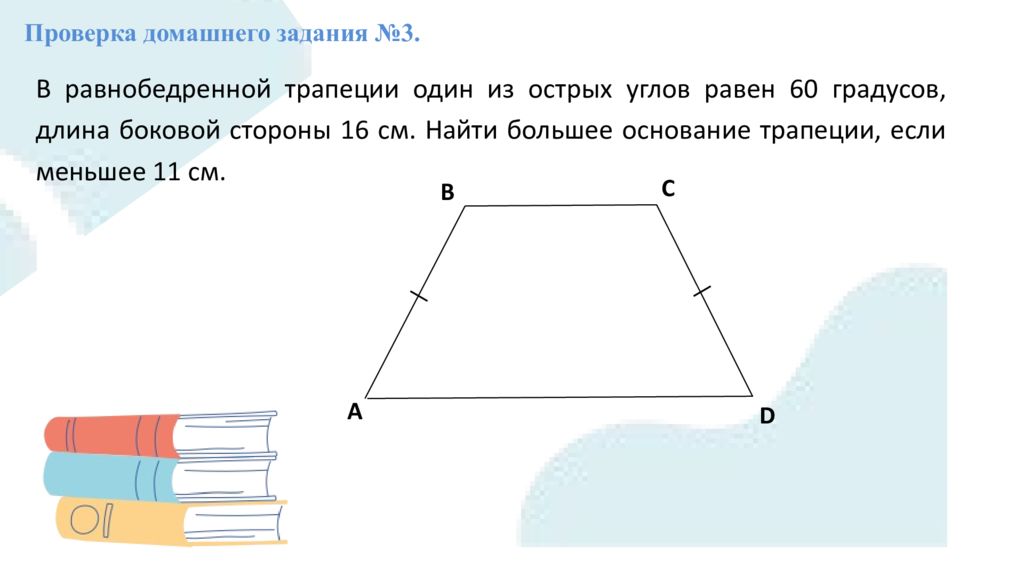
Проверка домашнего задания № 3. В равнобедренной трапеции один из острых углов равен 60 градусов, длина боковой стороны 16 см. Найти большее основание трапеции, если меньшее 11 см. A В С D
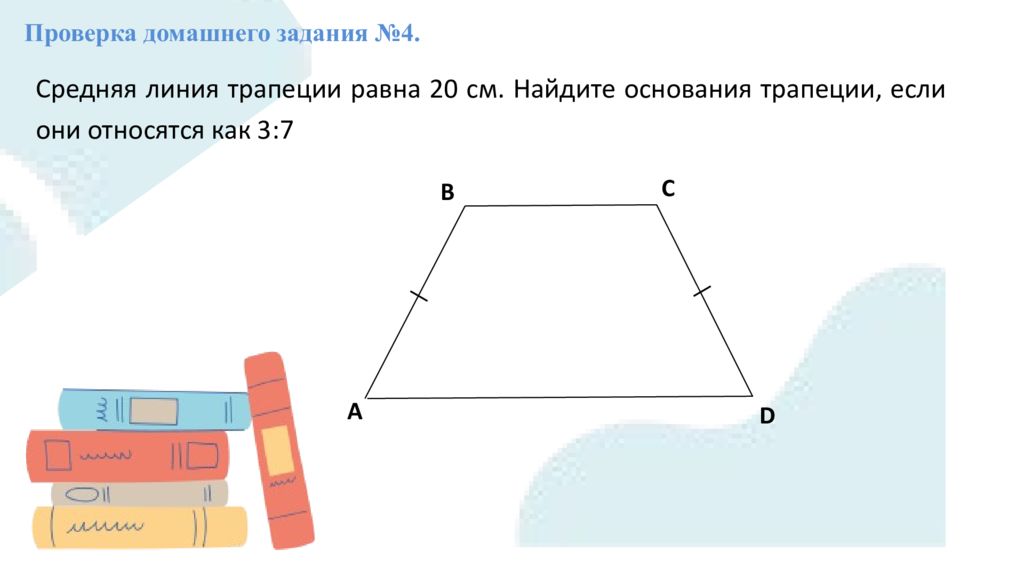
Проверка домашнего задания №4. Средняя линия трапеции равна 20 см. Найдите основания трапеции, если они относятся как 3:7 A В С D
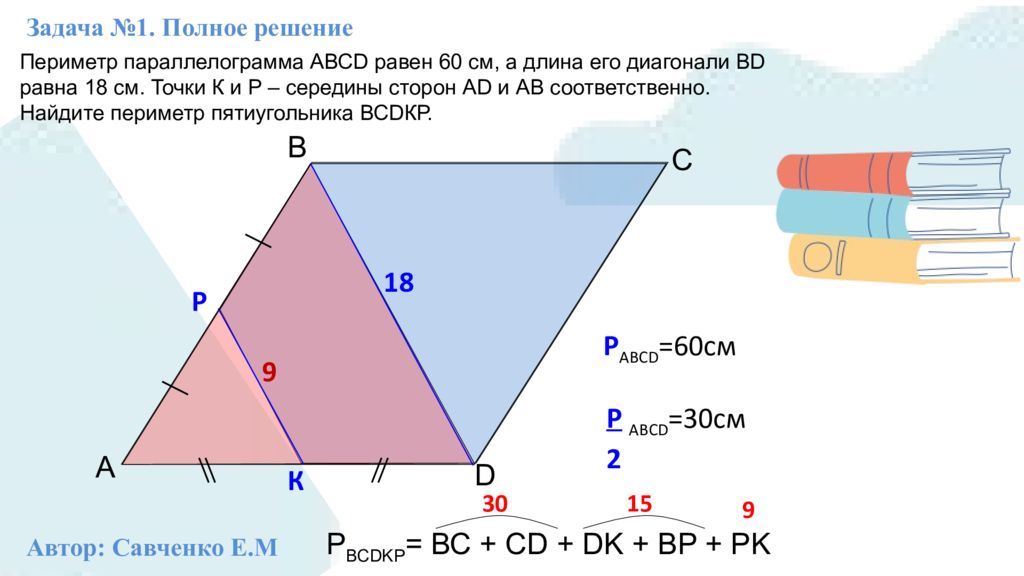
В А D Периметр параллелограмма АВС D равен 60 см, а длина его диагонали В D равна 18 см. Точки К и Р – середины сторон А D и АВ соответственно. Найдите периметр пятиугольника ВС D КР. С К Р 1 8 9 Р АВС D =60см Р АВС D =30см 2 Р ВС DKP = ВС + С D + DK + BP + PK 30 15 9 Задача №1. Полное решение Автор: Савченко Е.М
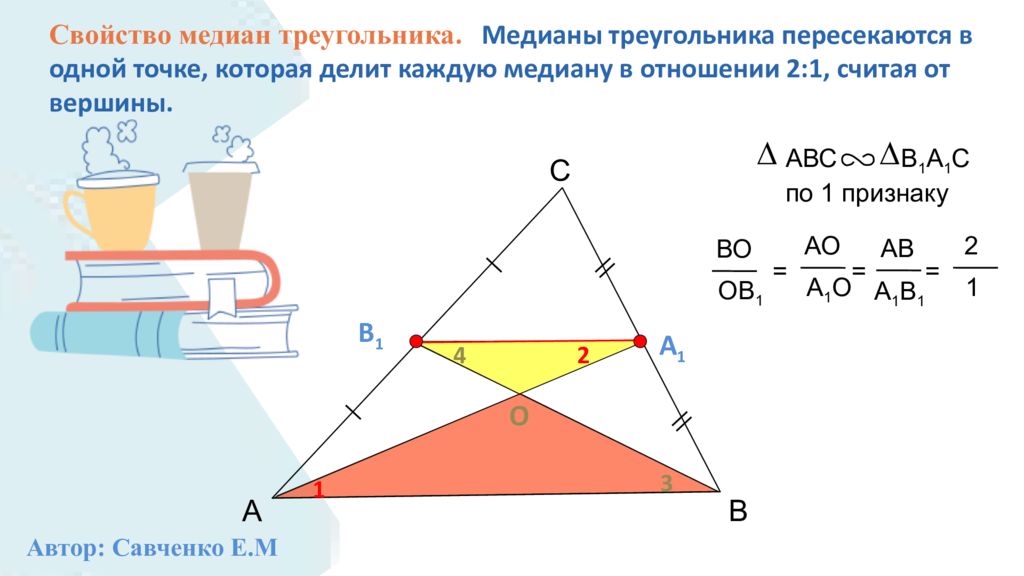
А С В В 1 А 1 О 1 2 3 4 A ВС В 1 А 1 С по 1 признаку ВО ОВ 1 = АО А 1 О АВ А 1 В 1 = = 2 1 Свойство медиан треугольника. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. Автор: Савченко Е.М
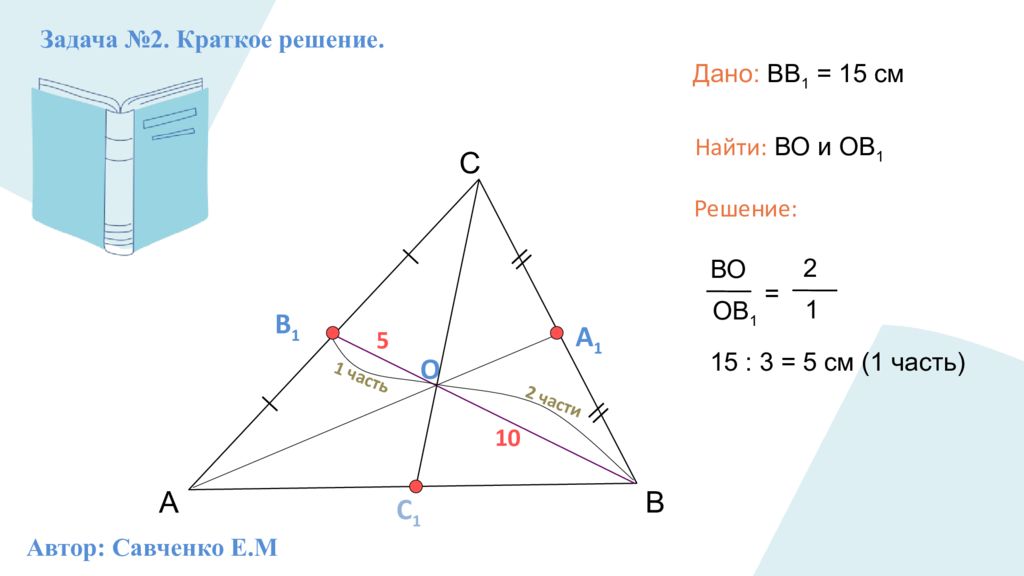
А С В Задача №2. Краткое решение. В 1 А 1 О ВО ОВ 1 = 2 1 С 1 Дано: ВВ 1 = 15 см Найти: ВО и ОВ 1 2 части 1 часть 15 : 3 = 5 см (1 часть) 10 5 Решение: Автор: Савченко Е.М
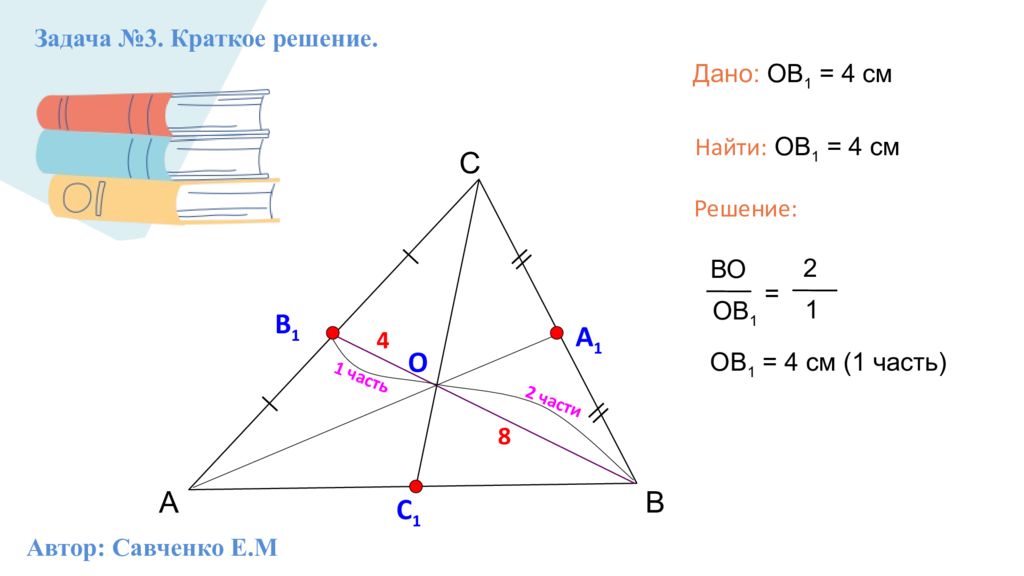
А С В Задача №3. Краткое решение. В 1 А 1 О С 1 2 части 1 часть 8 4 ВО ОВ 1 = 2 1 Дано: ОВ 1 = 4 см Найти: ОВ 1 = 4 см ОВ 1 = 4 см (1 часть) Решение: Автор: Савченко Е.М
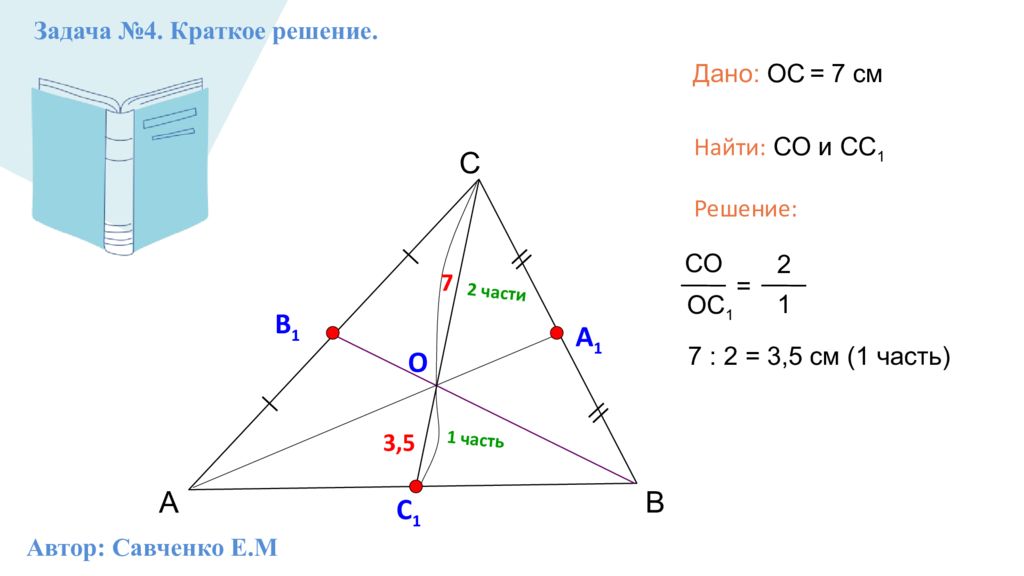
А С В Задача №4. Краткое решение. В 1 А 1 О СО ОС 1 = 2 1 С 1 2 части 1 часть 7 : 2 = 3,5 см (1 часть) 3,5 7 Дано: ОС = 7 см Найти: СО и СС 1 Решение: Автор: Савченко Е.М
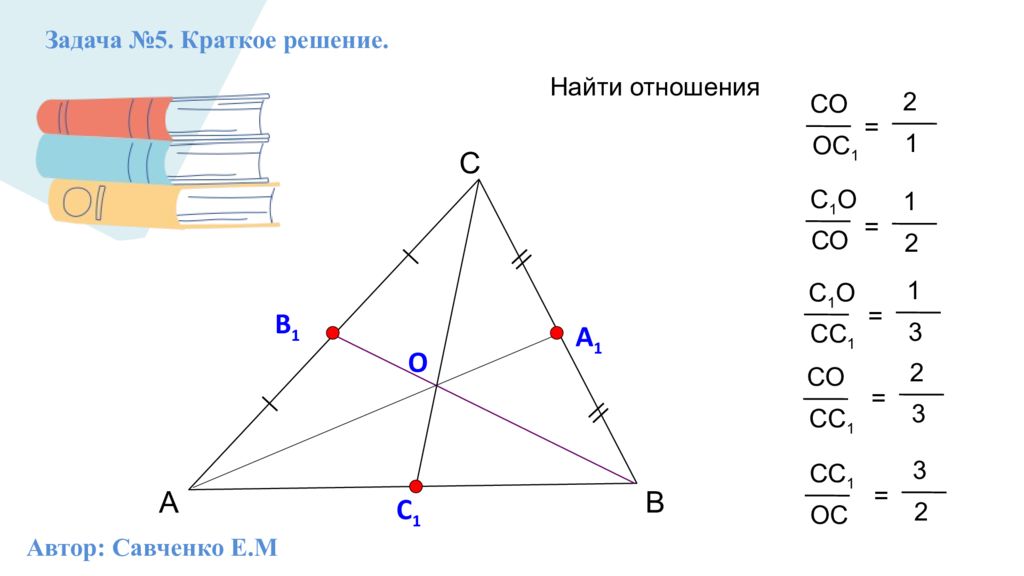
А С В Задача №5. Краткое решение. В 1 А 1 О СО ОС 1 = 2 1 С 1 Найти отношения С 1 О СО С 1 О СС 1 СО СС 1 СС 1 ОС = 1 2 = 1 3 = 2 3 = 3 2 Автор: Савченко Е.М
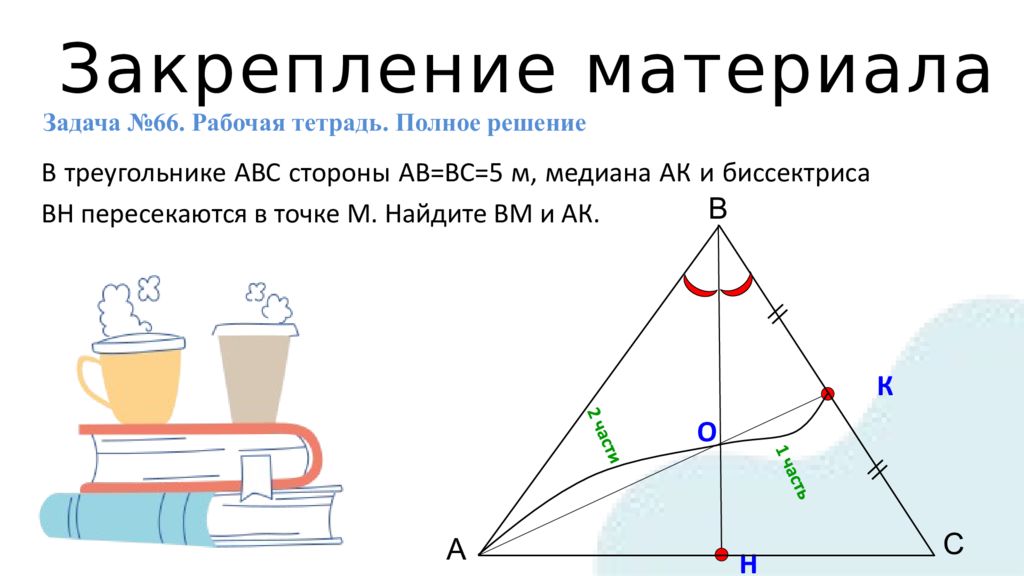
Закрепление материала Задача №66. Рабочая тетрадь. Полное решение В треугольнике АВС стороны АВ=ВС=5 м, медиана АК и биссектриса ВН пересекаются в точке М. Найдите ВМ и АК. А В С К О Н 2 части 1 часть
ДОМАШНЕЕ ЗАДАНИЕ
