8 класс ВЕРОЯТНОСТЬ И СТАТИСТИКА
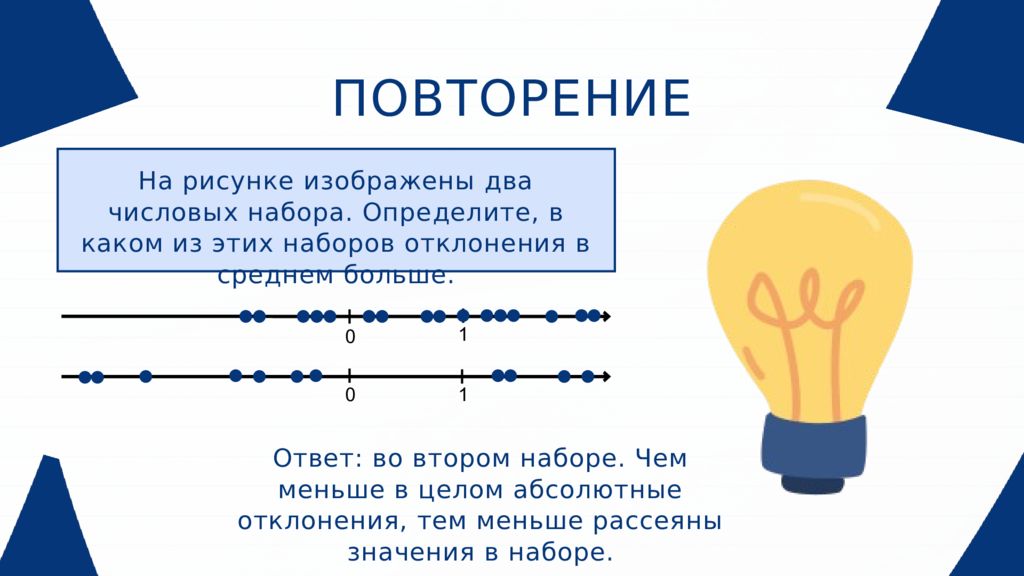
ПОВТОРЕНИЕ На рисунке изображены два числовых набора. Определите, в каком из этих наборов отклонения в среднем больше. 0 1 0 1 Ответ : во втором наборе. Чем меньше в целом абсолютные отклонения, тем меньше рассеяны значения в наборе.
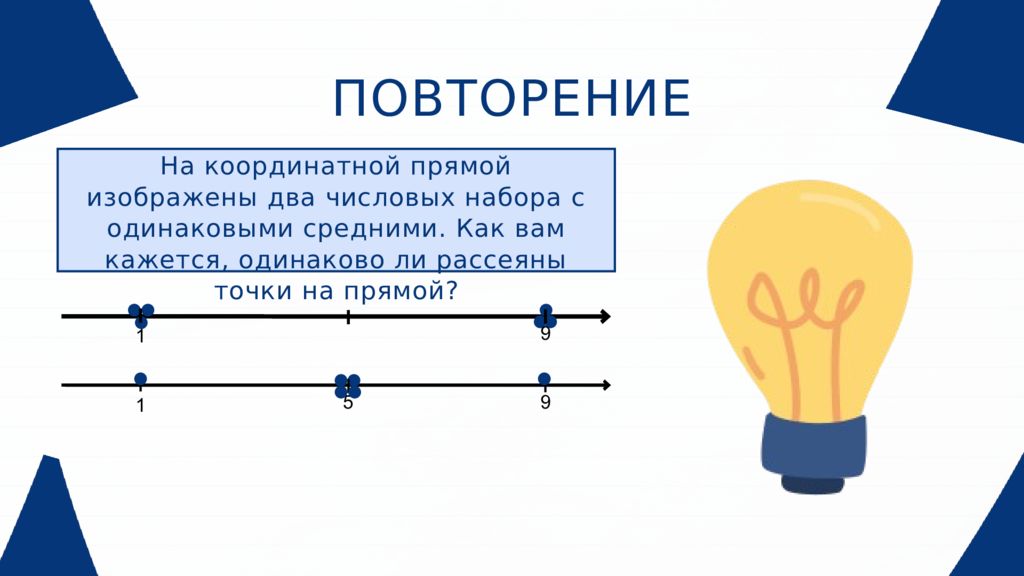
ПОВТОРЕНИЕ На координатной прямой изображены два числовых набора с одинаковыми средними. Как вам кажется, одинаково ли рассеяны точки на прямой? 1 9 1 9 5
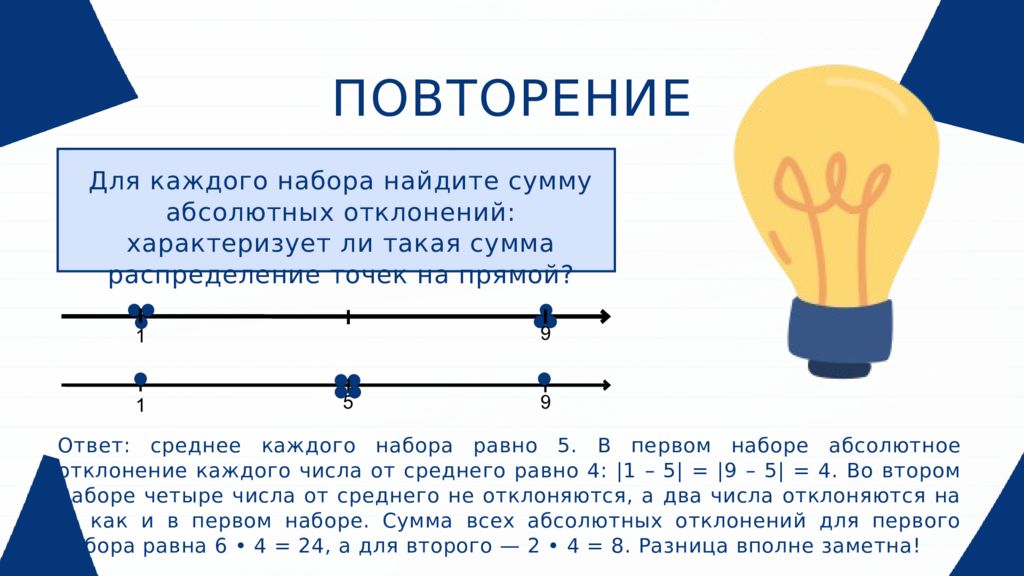
ПОВТОРЕНИЕ 1 9 1 9 5 Для каждого набора найдите сумму абсолютных отклонений: характеризует ли такая сумма распределение точек на прямой? Ответ : среднее каждого набора равно 5. В первом наборе абсолютное отклонение каждого числа от среднего равно 4: |1 – 5| = |9 – 5| = 4. Во втором наборе четыре числа от среднего не отклоняются, а два числа отклоняются на 4, как и в первом наборе. Сумма всех абсолютных отклонений для первого набора равна 6 • 4 = 24, а для второго — 2 • 4 = 8. Разница вполне заметна !
Наиболее полной характеристикой рассеивания чисел в массиве данных является набор их отклонений. Но когда набор велик, рассматривать все отклонения неудобно. Нужно взять какое-то среднее отклонение. Но среднее арифметическое отклонений не годится, поскольку оно у любого набора равна нулю. Чтобы судить о рассеивании, принято усреднять квадраты отклонений. Квадраты отклонений неотрицательны. Чем больше отклонения по модулю, тем больше будет средний квадрат отклонений. Эту величину называют дисперсией.
ДИСПЕРСИЯ ЧИСЛОВОГО НАБОРА
Среднее арифметическое квадратов отклонений от среднего арифметического называется дисперсией набора чисел. Обычно говорят короче: дисперсия — это средний квадрат отклонений. ОПРЕДЕЛЕНИЕ ФОРМУЛА S = (x - x) + (x - x) + (x - x) +... + (x - x) 1 2 3 n _ _ _ _ 2 2 2 2 n 2
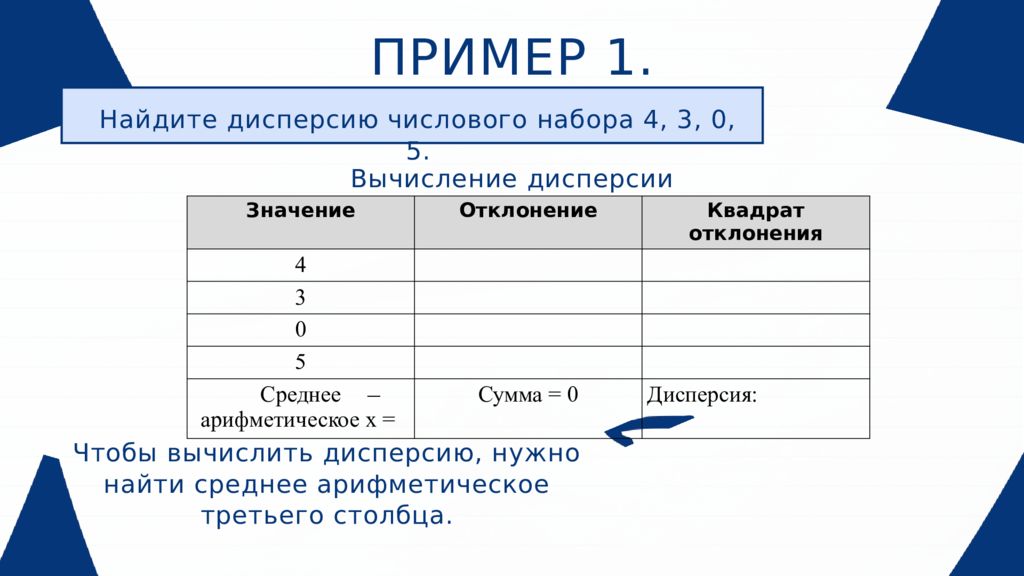
ПРИМЕР 1. Найдите дисперсию числового набора 4, 3, 0, 5. Вычисление дисперсии Чтобы вычислить дисперсию, нужно найти среднее арифметическое третьего столбца. Значение Отклонение Квадрат отклонения 4 3 0 5 Среднее арифметическое х = Сумма = 0 Дисперсия: _
ПРИМЕР 2. Найдите дисперсию числового набора 3, 3, 2, 4. Сравните этот набор из примера 1. Сравните среднее арифметическое. Сравните дисперсию. Изобразите два числовых набора на координатной прямой, сравните дисперсию и рассеивание двух наборов.
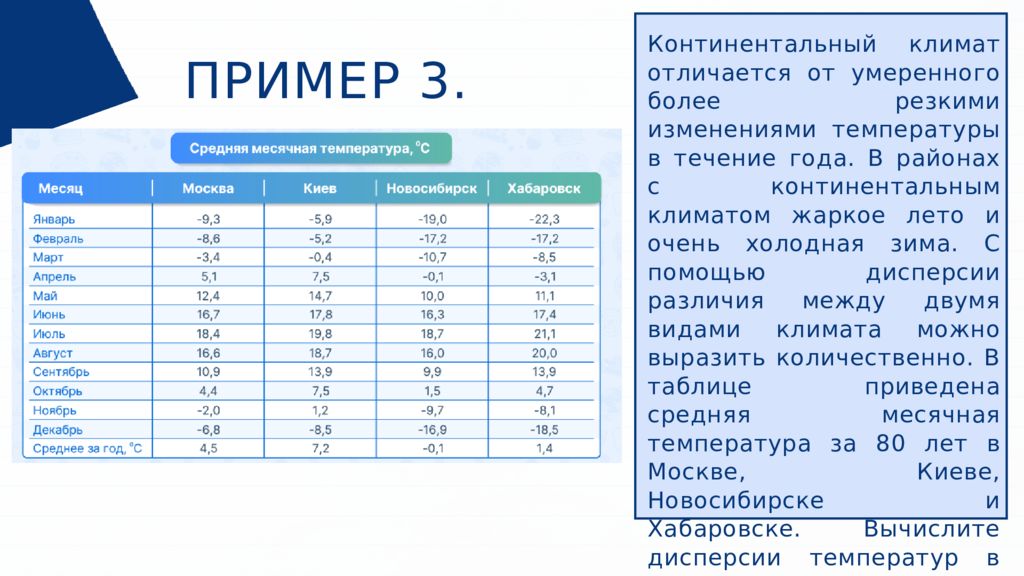
ПРИМЕР 3. Континентальный климат отличается от умеренного более резкими изменениями температуры в течение года. В районах с континентальным климатом жаркое лето и очень холодная зима. С помощью дисперсии различия между двумя видами климата можно выразить количественно. В таблице приведена средняя месячная температура за 80 лет в Москве, Киеве, Новосибирске и Хабаровске. Вычислите дисперсии температур в Москве, Киеве, Новосибирске и Хабаровске.
