Слайд 2
Название «Коллоидная химия» произошло от греческого слова - клееподобный. Термин «коллоид» ввел шотландский химик Томас Грэм в 1861 г. Он обнаружил, что некоторые вещества, например, желатина, агар-агар, кремниевая кислота, при выпаривании водного раствора не кристаллизуются, а образуют студенистые осадки. Кроме того, скорость их диффузии через мембрану очень мала. Некоторые из этих веществ обладают клеющим действием. Подобные вещества и были названы Грэмом «коллоидами». Томас Грэм (1805-1869) Историческая справка «Так как желатина представляет собой особый тип веществ, предложено обозначать вещества этого типа названием «коллоиды» и трактовать о такой форме агрегации, как о коллоидном состоянии материи. Противоположным коллоидному является кристаллическое состояние материи. Вещества, принадлежащие к данной форме состояния материи, следует обозначать названием «кристаллоиды». (Томас Грэм )
Слайд 3
П. П. фон Веймарн (1879-1935) 1906-1910 гг. – профессор Горного института Санкт-Петербурга П.П. фон Веймарн выдвинул фундаментальный принцип универсальности коллоидного состояния вещества: «Коллоидное состояние не является обособленным, обусловленным какими-либо особенностями состава вещества. При определенных условиях каждое вещество может быть в коллоидном состоянии» Прямым следствием принципа универсальности стало введение понятия о дисперсном (раздробленном) состоянии вещества и в связи с этим осознание важнейшей роли процессов, протекающих на межфазной поверхности. С этого времени коллоидная химия становится самостоятельной дисциплиной со своими объектами, методами и практическими приложениями Первая треть XX в. – период плодотворного и быстрого развития коллоидной химии К началу XX в. было открыто много веществ с типичными коллоидными свойствами, разработаны методы получения, очистки и стабилизации разнообразных коллоидных систем, созданы методы их изучения, в т.ч. и методы измерения размера частиц
Слайд 4
Лауреаты Нобелевской премии за работы в области коллоидной химии Р. Зигмонди австрийский химик, «за установление гетерогенной при-роды коллоидных растворов и за раз-работанные в этой связи методы, име-ющие фундамен-тальное значение в современной коллоидной химии» 1925 г. И. Ленгмюр американский физикохимик, «за открытия и исследования в области химии поверхностных явлений» 1932 г. Ж. Перрен французский физик, «за работу по дискретной природе материи и, в особенности, за открытие седиментационно-диффузионного равновесия» 1926 г. Т. Сведберг шведский ученый, «за работы в области дисперсных систем» (прежде всего за создание ультрацентрифуги для определения размеров высоко-дисперсных частиц и макромолекул) 1926 г.
Слайд 5
А. В. Думанский – один из основоположников коллоидной химии в России 1904 г. – организовал первую в стране лабораторию коллоидной химии (г. Киев) 1932 г. – по его инициативе создан Государственный НИИ коллоидной химии (г. Воронеж) 1935 г. – основал «Коллоидный журнал» 1934 г. – состоялась Первая Всесоюзная коллоидная конференция (г. Воронеж) Автор учебного пособия «Дисперсность и коллоидное состояние вещества» (1932 и 1934 гг.), оригинального учебника «Учение о коллоидах», который трижды переиздавался В 1932 г. А.В. Думанский удостоен большой Менделеевской премии А. В. Думанский (1880-1967)
Слайд 6
Современное определение предметной области коллоидной химии Коллоидная химия – наука о дисперсных системах и поверхностных явлениях Эмульсии Пены Пасты Порошки Суспензии Золи Примеры дисперсных систем Поверхностные явления – это процессы, протекающие на границе раздела фаз
Слайд 8
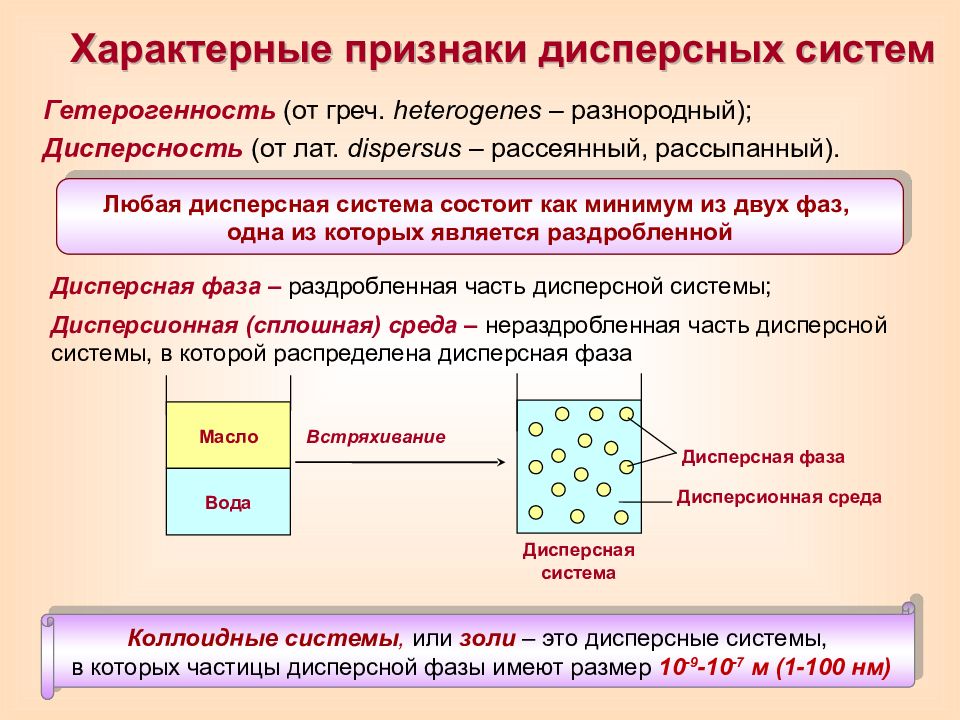
Гетерогенность (от греч. heterogenes – разнородный); Дисперсность (от лат. dispersus – рассеянный, рассыпанный). Характерные признаки дисперсных систем Встряхивание Дисперсная система Масло Вода Дисперсная фаза Дисперсионная среда Коллоидные системы, или золи – это дисперсные системы, в которых частицы дисперсной фазы имеют размер 10 -9 -10 -7 м (1-100 нм) Дисперсная фаза – раздробленная часть дисперсной системы; Дисперсионная (сплошная) среда – нераздробленная часть дисперсной системы, в которой распределена дисперсная фаза Любая дисперсная система состоит как минимум из двух фаз, одна из которых является раздробленной
Слайд 9
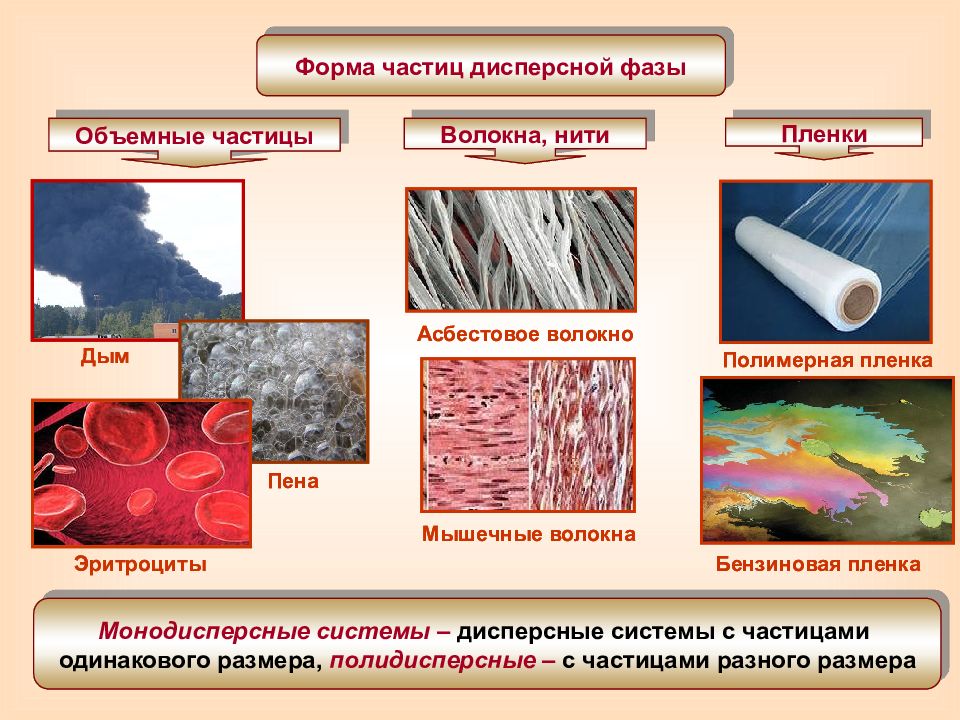
Бензиновая пленка Дым Пена Эритроциты Асбестовое волокно Мышечные волокна Полимерная пленка Форма частиц дисперсной фазы Объемные частицы Волокна, нити Пленки Монодисперсные системы – дисперсные системы с частицами одинакового размера, полидисперсные – с частицами разного размера Бензиновая пленка Дым Пена Эритроциты Асбестовое волокно Мышечные волокна Полимерная пленка Форма частиц дисперсной фазы Объемные частицы Волокна, нити Пленки Монодисперсные системы – дисперсные системы с частицами одинакового размера, полидисперсные – с частицами разного размера
Слайд 10
Количественные характеристики дисперсных систем 3) Частичная концентрация n – число частиц дисперсной фазы в единице объема системы, м -3 1) Дисперсность D – величина, обратная определяющему (характерному) размеру частиц а : D = 1/a 2) Удельная поверхность S уд – площадь межфазной поверхности S, отнесенная к единице массы m или объема V дисперсной фазы: S уд = S/m, м 2 /кг или S уд = S/V, м -1 Для монодисперсных систем: S уд = k/a = kD k – коэффициент, зависящий от формы частиц. Для частиц кубической формы с ребром а Для частиц сферической формы с радиусом r а r
Слайд 11
а, м S уд, м -1 1 6 10 -1 60 10 -5 6 10 5 10 -7 6 10 7 10 -9 6 10 9 Удельная поверхность и дисперсность резко возрастают! при уменьшении размера частиц дисперсной фазы. Максимальную удельную поверхность (порядка 10 7 – 10 9 м -1 ) имеют частицы дисперсной фазы в коллоидных растворах Поэтому на поведение дисперсных систем, имеющих развитую поверхность раздела, преобладающее влияние оказывают процессы, протекающие на поверхности, а не внутри фазы! Для частиц кубической формы с ребром а
Слайд 12
Основные свойства дисперсных систем определяются Раздробленность и большая удельная поверхность раздела фаз обусловливают значительный избыток поверхностной энергии на межфазной поверхности. Жидкость Газ Межмолекулярные взаимодействия внутри фазы и на поверхности раздела фаз НЕСКОМПЕНСИРОВАННОЙ ПОВЕРХНОСТНОЙ ЭНЕРГИЕЙ! Общая поверхностная энергия системы определяется площадью поверхности S и удельной поверхностной энергией , называемой поверхностным натяжением : G s = S Поверхностное натяжение – это работа термодинамиче - ски обратимого процесса образования единицы площади но- вой поверхности при постоянных температуре Т, давлении р и составе жидкости Поверхностное натяжение характеризует различия в интенсивности межмолекулярных взаимодействий граничащих фаз. Чем больше эти различия, тем больше . Поверхностное натяжение на границе двух конденсиро- ванных фаз называет межфазовым. Поверхностное натяжение с ростом температуры снижается. [ ] = Дж/м 2 = Н/м = - A обр / dS Жидкость , мДж/м 2 Вода 72,75 Сырое молоко 45-60 Подсолн. масло 33 Ртуть 460 При Т = 293 К
Слайд 14
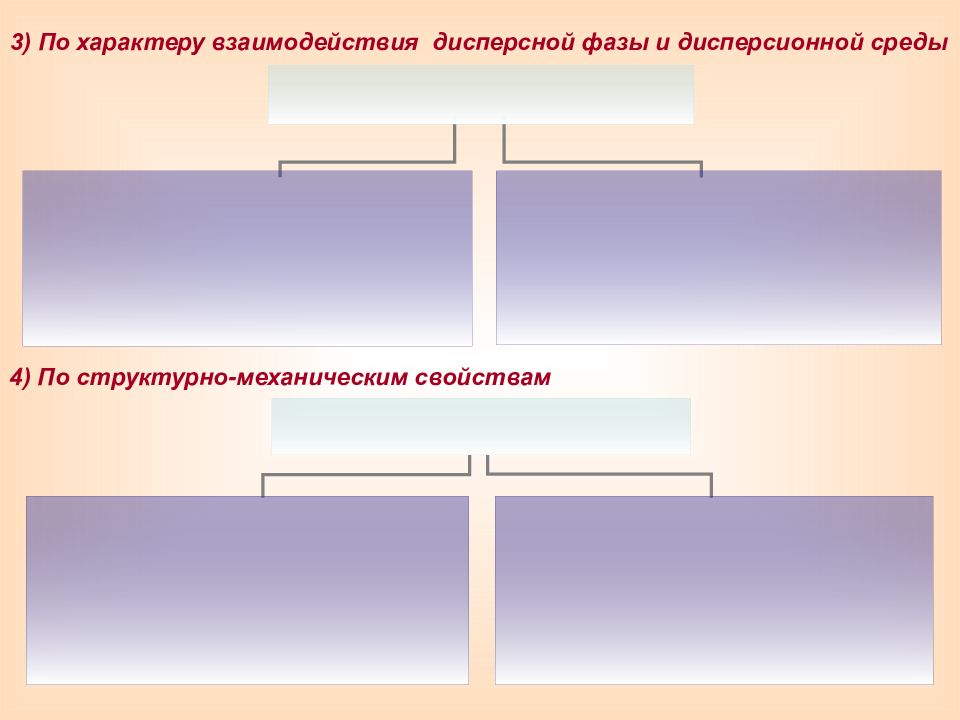
Принципы классификации дисперсных систем По степени дисперсности; По агрегатному состоянию дисперсной фазы и дисперсионной среды; По характеру взаимодействия дисперсной фазы и дисперсионной среды; По структурно-механическим свойствам.
Слайд 15
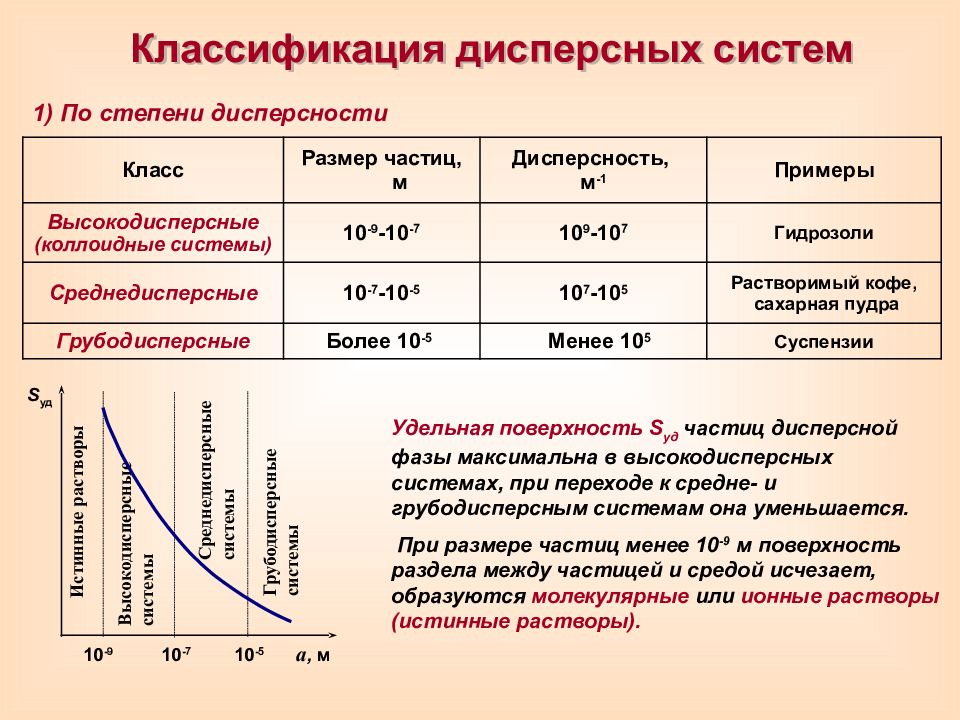
Классификация дисперсных систем Класс Размер частиц, м Дисперсность, м -1 Примеры Высокодисперсные (коллоидные системы) 10 -9 -10 -7 10 9 -10 7 Гидрозоли Среднедисперсные 10 -7 -10 -5 10 7 -10 5 Растворимый кофе, сахарная пудра Грубодисперсные Более 10 -5 Менее 10 5 Суспензии 1) По степени дисперсности Удельная поверхность S уд частиц дисперсной фазы максимальна в высокодисперсных системах, при переходе к средне- и грубодисперсным системам она уменьшается. При размере частиц менее 10 -9 м поверхность раздела между частицей и средой исчезает, образуются молекулярные или ионные растворы (истинные растворы). S уд Истинные растворы Высокодисперсные системы Среднедисперсные системы Грубодисперсные системы 10 -9 10 -7 10 -5 a, м
Слайд 16: 2) По агрегатному состоянию дисперсной фазы и дисперсионной среды
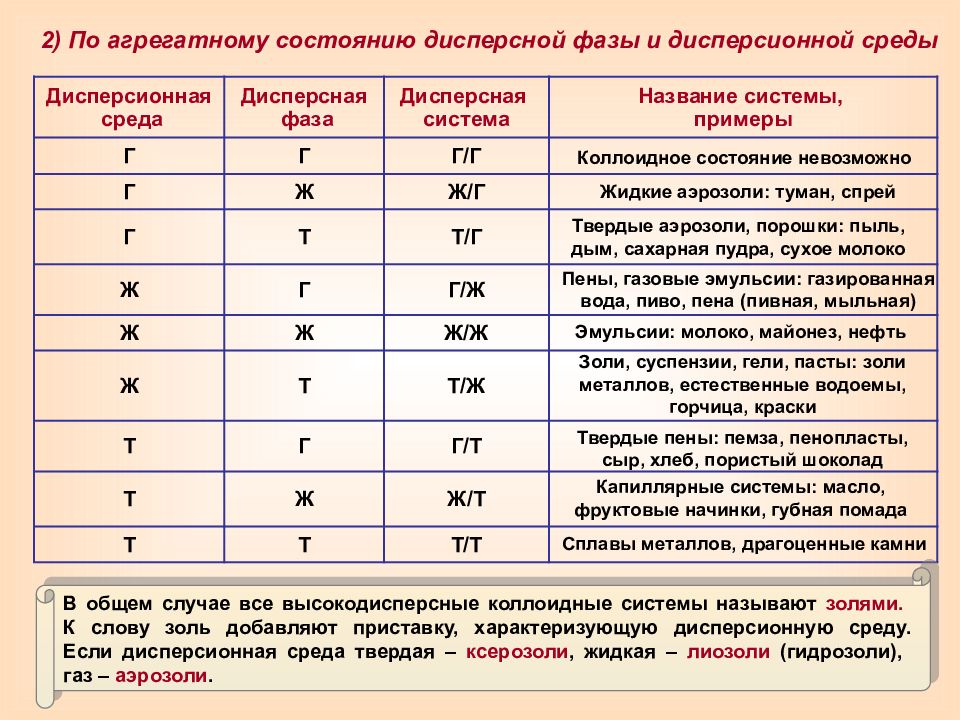
Дисперсионная среда Дисперсная фаза Дисперсная система Название системы, примеры Г Г Г/Г Г Ж Ж/Г Г Т Т/Г Ж Г Г/Ж Ж Ж Ж/Ж Ж Т Т/Ж Т Г Г/Т Т Ж Ж/Т Т Т Т/Т Коллоидное состояние невозможно Жидкие аэрозоли: туман, спрей Твердые аэрозоли, порошки: пыль, дым, сахарная пудра, сухое молоко Пены, газовые эмульсии: газированная вода, пиво, пена (пивная, мыльная) Эмульсии: молоко, майонез, нефть Золи, суспензии, гели, пасты: золи металлов, естественные водоемы, горчица, краски Твердые пены: пемза, пенопласты, сыр, хлеб, пористый шоколад Капиллярные системы: масло, фруктовые начинки, губная помада Сплавы металлов, драгоценные камни В общем случае все высокодисперсные коллоидные системы называют золями. К слову золь добавляют приставку, характеризующую дисперсионную среду. Если дисперсионная среда твердая – ксерозоли, жидкая – лиозоли (гидрозоли), газ – аэрозоли.
Слайд 17: 3) По характеру взаимодействия дисперсной фазы и дисперсионной среды
4) По структурно-механическим свойствам
Слайд 19
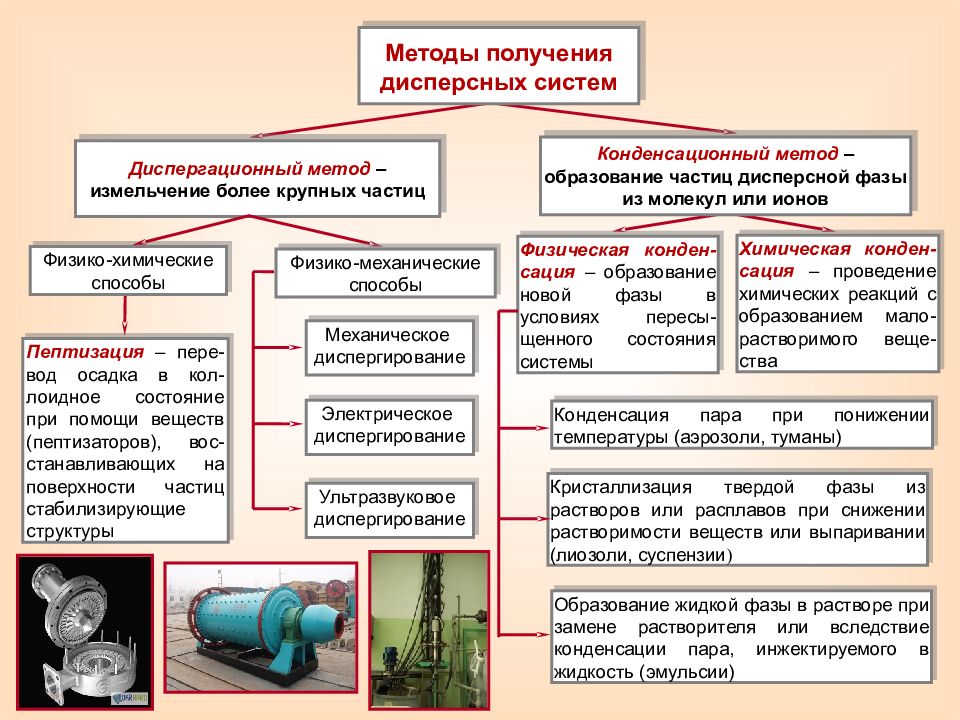
Методы получения дисперсных систем Диспергационный метод – измельчение более крупных частиц Конденсационный метод – образование частиц дисперсной фазы из молекул или ионов Пептизация – пере-вод осадка в кол-лоидное состояние при помощи веществ (пептизаторов), вос-станавливающих на поверхности частиц стабилизирующие структуры Химическая конден-сация – проведение химических реакций с образованием мало-растворимого веще-ства Образование жидкой фазы в растворе при замене растворителя или вследствие конденсации пара, инжектируемого в жидкость (эмульсии) Конденсация пара при понижении температуры (аэрозоли, туманы) Кристаллизация твердой фазы из растворов или расплавов при снижении растворимости веществ или выпаривании (лиозоли, суспензии ) Физическая конден-сация – образование новой фазы в условиях пересы-щенного состояния системы Физико-химические способы Механическое диспергирование Электрическое диспергирование Ультразвуковое диспергирование Физико-механические способы
Слайд 21
ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ Лиофобные дисперсные системы, обладающие большим избытком поверхностной энергии, термодинамически неустойчивы ; в них самопро-извольно протекают процессы, приводящие к снижению свободной энергии Поверхностные явления – это процессы, протекающие на границе раздела фаз и сопровождающиеся само-произвольным снижением поверхностной энергии G s Следовательно, снижение поверхностной энергии G s может происходить за счет уменьшения межфазной поверхности S и поверхностного натяжения G s = S При p, T = const
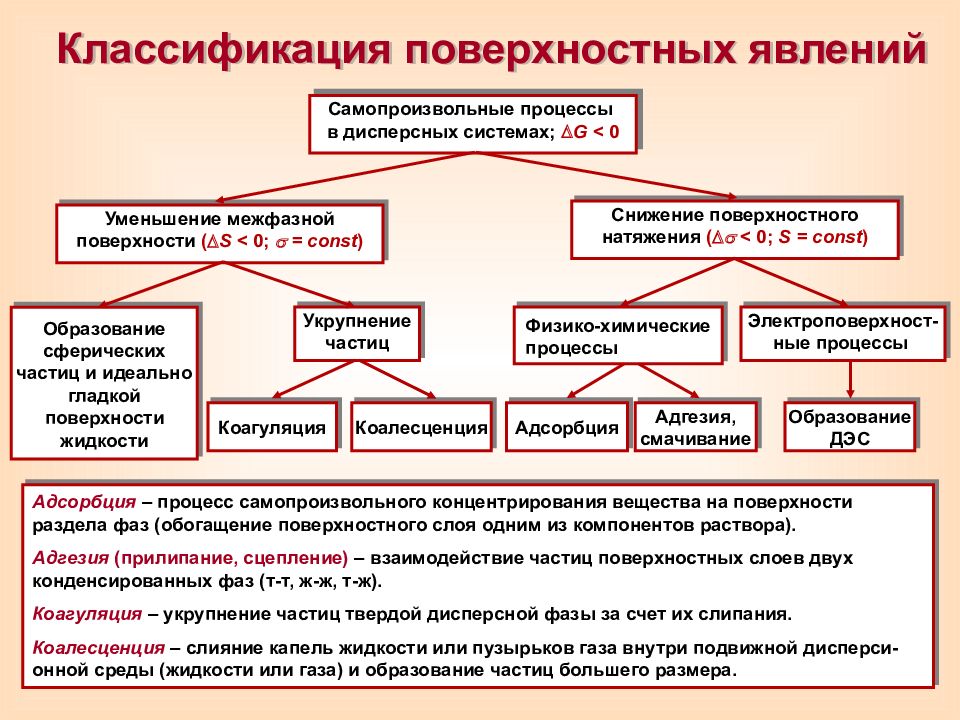
Слайд 22: Классификация поверхностных явлений
Самопроизвольные процессы в дисперсных системах; G < 0 Уменьшение межфазной поверхности ( S < 0; = const ) Снижение поверхностного натяжения ( < 0 ; S = const ) Укрупнение частиц Образование сферических частиц и идеально гладкой поверхности жидкости Физико-химические процессы Электроповерхност-ные процессы Коагуляция Коалесценция Адсорбция Адгезия, смачивание Образование ДЭС Адсорбция – процесс самопроизвольного концентрирования вещества на поверхности раздела фаз (обогащение поверхностного слоя одним из компонентов раствора). Адгезия (прилипание, сцепление) – взаимодействие частиц поверхностных слоев двух конденсированных фаз (т-т, ж-ж, т-ж ). Коагуляция – укрупнение частиц твердой дисперсной фазы за счет их слипания. Коалесценция – c лияние капель жидкости или пузырьков газа внутри подвижной дисперси-онной среды (жидкости или газа) и образование частиц большего размера.
Слайд 24
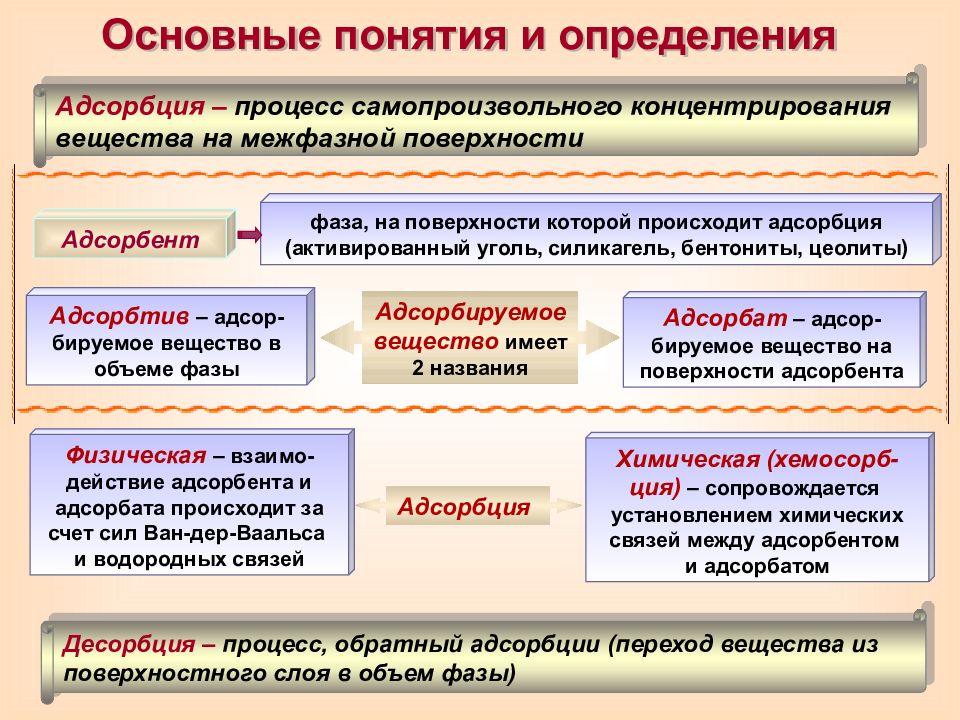
Основные понятия и определения Адсорбция – процесс самопроизвольного концентрирования вещества на межфазной поверхности Десорбция – процесс, обратный адсорбции (переход вещества из поверхностного слоя в объем фазы) Физическая – взаимо-действие адсорбента и адсорбата происходит за счет сил Ван-дер-Ваальса и водородных связей Химическая (хемосорб-ция) – сопровождается установлением химических связей между адсорбентом и адсорбатом Адсорбция Адсорбент фаза, на поверхности которой происходит адсорбция (активированный уголь, силикагель, бентониты, цеолиты) Адсорбтив – адсор-бируемое вещество в объеме фазы Адсорбат – адсор-бируемое вещество на поверхности адсорбента Адсорбируемое вещество имеет 2 названия
Слайд 25
Абсолютная адсорбция А i – количество i -го компонента в поверхностном слое, отнесенное к площади слоя S или к массе адсорбента m : Способы выражения величины адсорбции s n i A i =, моль/м 2 s n i S A i =, моль/кг s n i m или Избыточная (гиббсовская) адсорбция Г i – избыток i -го компонента в поверхностном слое по сравнению с его количеством в таком же объеме, но внутри фазы, отнесенный к площади слоя: A i =, моль/м 2 s n i – n i S v Если концентрация адсорбируемого вещества на поверхности значительно превышает его концентрацию в объеме, можно принять, что Г = А. где - количество i -го компонента в объеме фазы v n i
Слайд 26
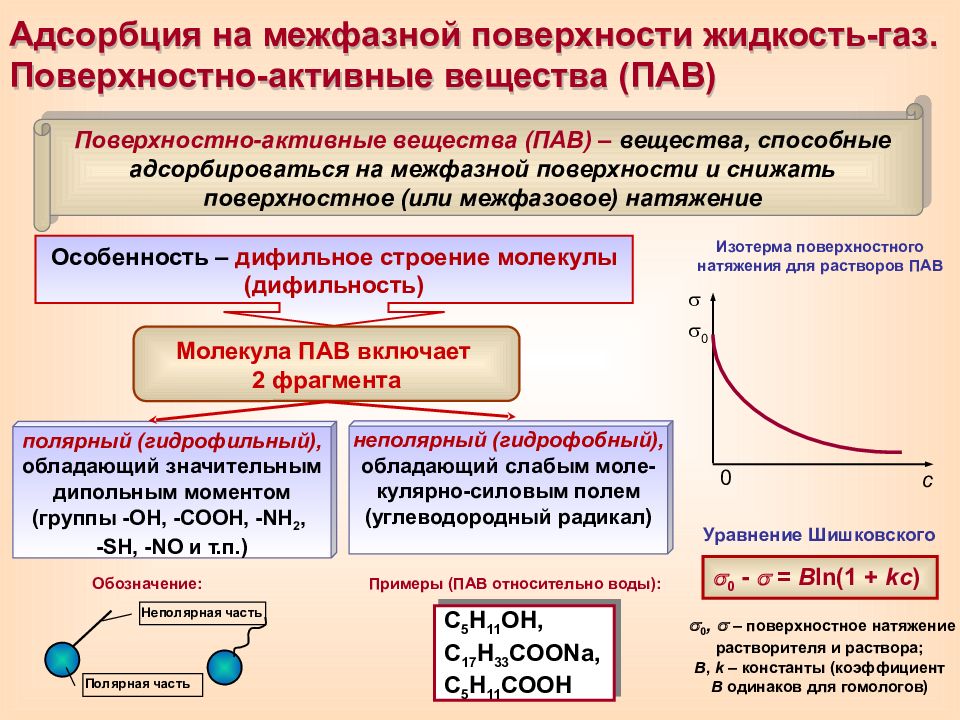
Адсорбция на межфазной поверхности жидкость-газ. Поверхностно-активные вещества (ПАВ) Поверхностно-активные вещества (ПАВ) – вещества, способные адсорбироваться на межфазной поверхности и снижать поверхностное (или межфазовое) натяжение Особенность – дифильное строение молекулы (дифильность) Молекула ПАВ включает 2 фрагмента полярный (гидрофильный), обладающий значительным дипольным моментом (группы -ОН, -СООН, -N Н 2, - S Н, - NO и т.п.) неполярный (гидрофобный), обладающий слабым моле- кулярно-силовым полем (углеводородный радикал) Примеры (ПАВ относительно воды): Неполярная часть Полярная часть Обозначение: С 5 Н 11 ОН, С 17 Н 33 СОО Na, С 5 Н 11 СООН с 0 Изотерма поверхностного натяжения для растворов ПАВ 0 Уравнение Шишковского 0 - = В ln(1 + kc ) 0, – поверхностное натяжение растворителя и раствора; В, k – константы (коэффициент В одинаков для гомологов)
Слайд 27
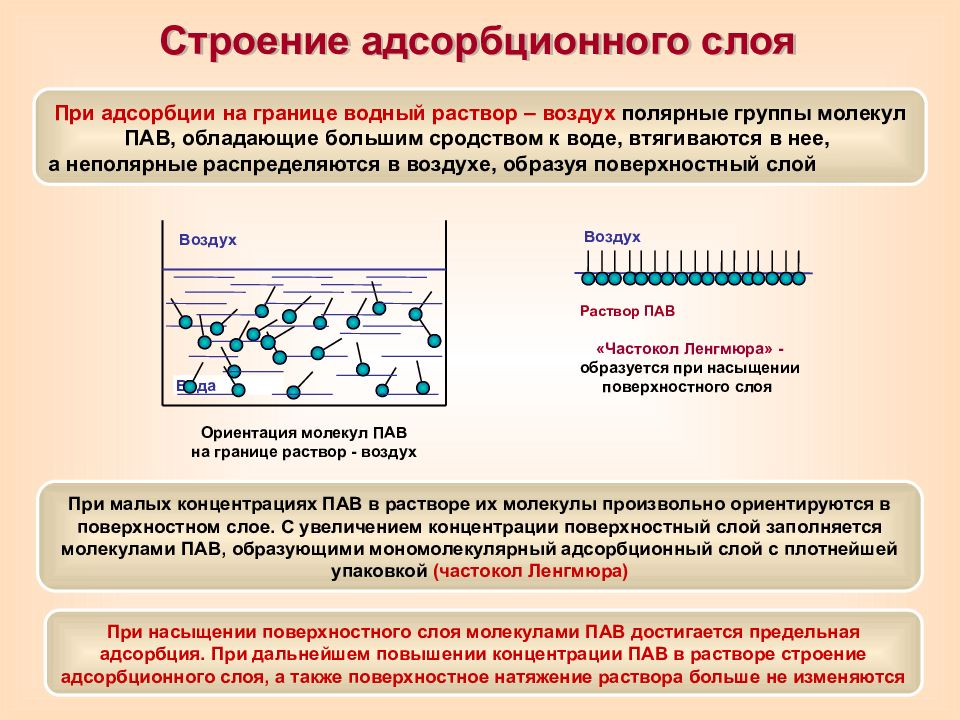
Раствор ПАВ Вода Воздух Воздух Раствор ПАВ «Частокол Ленгмюра » - образуется при насыщении поверхностного слоя Ориентация молекул ПАВ на границе раствор - воздух При адсорбции на границе водный раствор – воздух полярные группы молекул ПАВ, обладающие большим сродством к воде, втягиваются в нее, а неполярные распределяются в воздухе, образуя поверхностный слой Строение адсорбционного слоя При малых концентрациях ПАВ в растворе их молекулы произвольно ориентируются в поверхностном слое. С увеличением концентрации поверхностный слой заполняется молекулами ПАВ, образующими мономолекулярный адсорбционный слой с плотнейшей упаковкой (частокол Ленгмюра) При насыщении поверхностного слоя молекулами ПАВ достигается предельная адсорбция. При дальнейшем повышении концентрации ПАВ в растворе строение адсорбционного слоя, а также поверхностное натяжение раствора больше не изменяются
Слайд 28
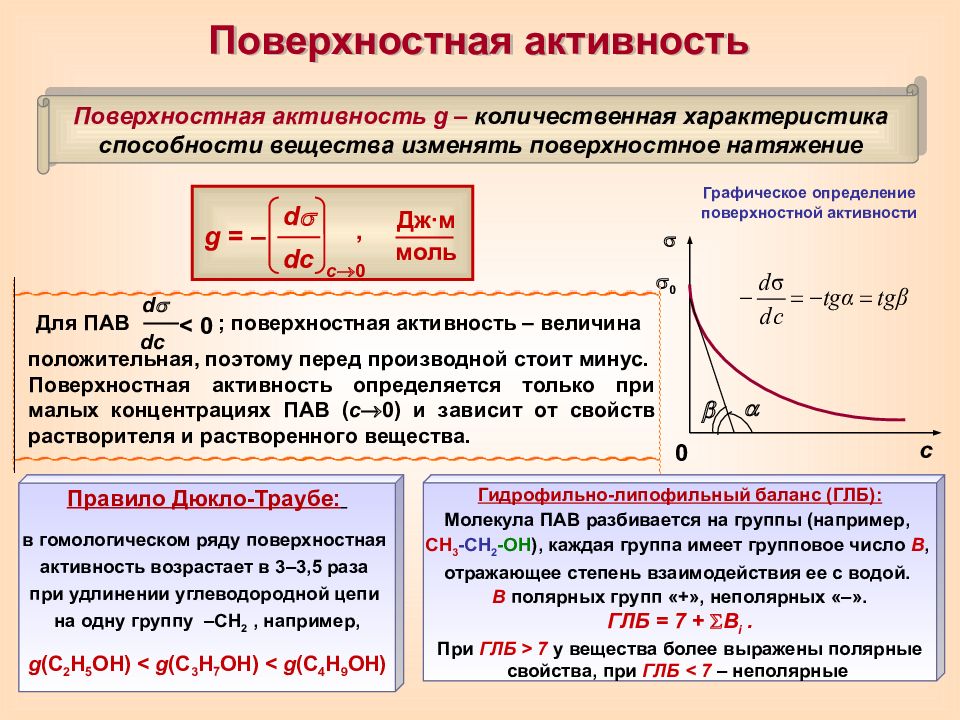
Поверхностная активность Поверхностная активность g – количественная характеристика способности вещества изменять поверхностное натяжение Графическое определение поверхностной активности 0 с 0 g = – d d c Дж ∙м моль , Правило Дюкло-Траубе: в гомологическом ряду поверхностная активность возрастает в 3–3,5 раза при удлинении углеводородной цепи на одну группу –СН 2, например, g ( С 2 Н 5 ОН ) < g ( С 3 Н 7 ОН ) < g ( С 4 Н 9 ОН ) Гидрофильно-липофильный баланс (ГЛБ): Молекула ПАВ разбивается на группы (например, СН 3 -СН 2 -ОН ), каждая группа имеет групповое число В, отражающее степень взаимодействия ее с водой. В полярных групп «+», неполярных «–». ГЛБ = 7 + В i. При ГЛБ > 7 у вещества более выражены полярные свойства, при ГЛБ < 7 – неполярные Для ПАВ ; поверхностная активность – величина положительная, поэтому перед производной стоит минус. Поверхностная активность определяется только при малых концентрациях ПАВ ( c 0 ) и зависит от свойств растворителя и растворенного вещества. c 0 d d c < 0
Слайд 29
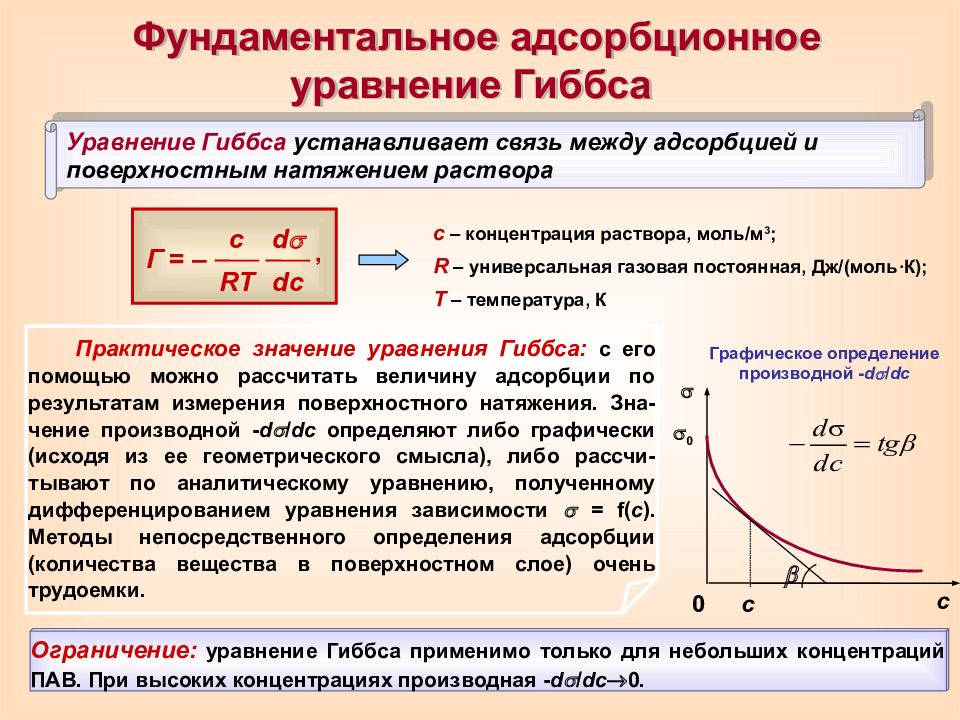
Фундаментальное адсорбционное уравнение Гиббса Практическое значение уравнения Гиббса: с его помощью можно рассчитать величину адсорбции по результатам измерения поверхностного натяжения. Зна-чение производной - d / dc определяют либо графически (исходя из ее геометрического смысла), либо рассчи-тывают по аналитическому уравнению, полученному дифференцированием уравнения зависимости = f ( с ). Методы непосредственного определения адсорбции (количества вещества в поверхностном слое) очень трудоемки. Уравнение Гиббса устанавливает связь между адсорбцией и поверхностным натяжением раствора Г = – d d c , с RT Графическое определение производной - d / dc 0 с 0 с с – концентрация раствора, моль/м 3 ; R – универсальная газовая постоянная, Дж/(моль ∙К); Т – температура, К Ограничение: уравнение Гиббса применимо только для небольших концентраций ПАВ. При высоких концентрациях производная - d / dc 0.
Слайд 30
Уравнение мономолекулярной адсорбции Ленгмюра Общий вид изотермы адсорбции 0 Г с Г m а x Изотермы адсорбции гомологов 0 Г с Г m а x Экспериментально полученные изотермы адсорбции различных ПАВ имели горизонтальный участок. Для гомологов все изотермы в пределе сливаются. Это возможно, если: 1) все молекулы гомологов, независимо от длины УВ-радикала, занимают на межфазной поверхности одинаковую площадь; 2) адсорбционный слой имеет толщину не более одной молекулы, т.е. мономолекулярный. Уравнение Гиббса не описывает всю экспериментально полученную изотерму адсорбции! Таким образом, уравнение Ленгмюра описывает всю изотерму мономолекулярной адсорбции, включая ее горизонтальный участок Уравнение Ленгмюра: Г max – предельная адсорбция; k – константа адсорбционно-десорбционного равновесия Анализ уравнения: в сильно разбавленных растворах, когда kc << 1, уравнение принимает вид: Г=Г max kc (начальный (прямолинейный) участок изотермы адсорбции ) ; в концентрированных растворах kc >> 1, тогда Г = Г max ( горизонтальный участок изотермы)
Слайд 31
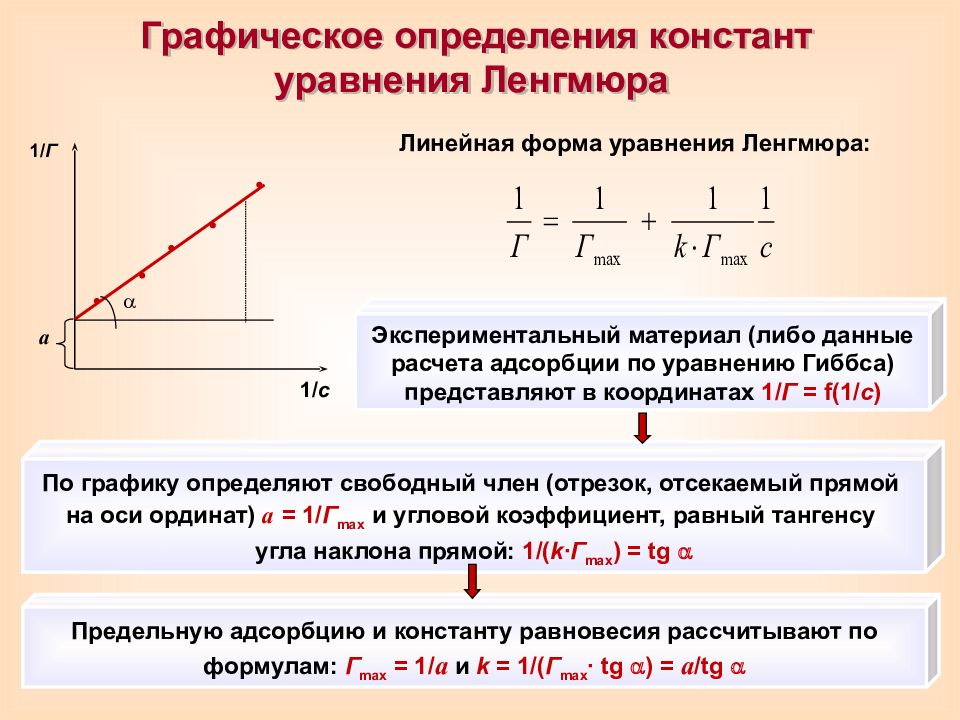
Графическое определения констант уравнения Ленгмюра 1/ Г 1/ с а Линейная форма уравнения Ленгмюра: Экспериментальный материал (либо данные расчета адсорбции по уравнению Гиббса) представляют в координатах 1/ Г = f(1/ c ) По графику определяют свободный член (отрезок, отсекаемый прямой на оси ординат) а = 1/ Г max и угловой коэффициент, равный тангенсу угла наклона прямой: 1/( k ∙ Г max ) = tg Предельную адсорбцию и константу равновесия рассчитывают по формулам: Г max = 1/ a и k = 1/( Г max ∙ tg ) = а / tg
Слайд 32
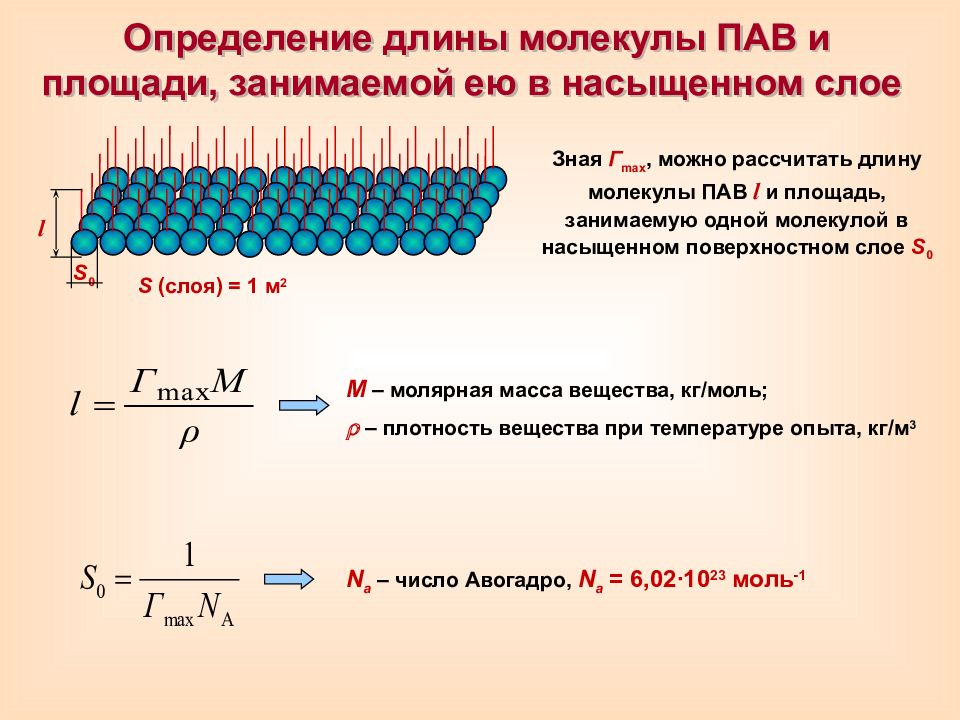
Определение длины молекулы ПАВ и площади, занимаемой ею в насыщенном слое l S 0 S ( слоя) = 1 м 2 Зная Г max, можно рассчитать длину молекулы ПАВ l и площадь, занимаемую одной молекулой в насыщенном поверхностном слое S 0 N a – число Авогадро, N a = 6,02 ∙10 23 моль -1 М – молярная масса вещества, кг/моль; – плотность вещества при температуре опыта, кг /м 3
Слайд 33
Связь между константами уравнений Шишковского и Ленгмюра Уравнение Шишковского 0 - = В ln(1 + kc ) В, k – константы Г = – d d c с RT Уравнение Гиббса Уравнение Ленгмюра Г max, k – константы При малых концентрациях ПАВ расчет адсорбции по уравнениям Гиббса и Ленгмюра дает близкие результаты, т.е. правые части этих уравнений можно приравнять: После интегрирования в определенных пределах от 0 до с и от 0 до : Сопоставляя с уравнением Шишковского: Константа k в уравнениях Шишковского и Ленгмюра имеет один и тот же смысл – это константа адсорбционно-десорбционного равновесия
Слайд 34
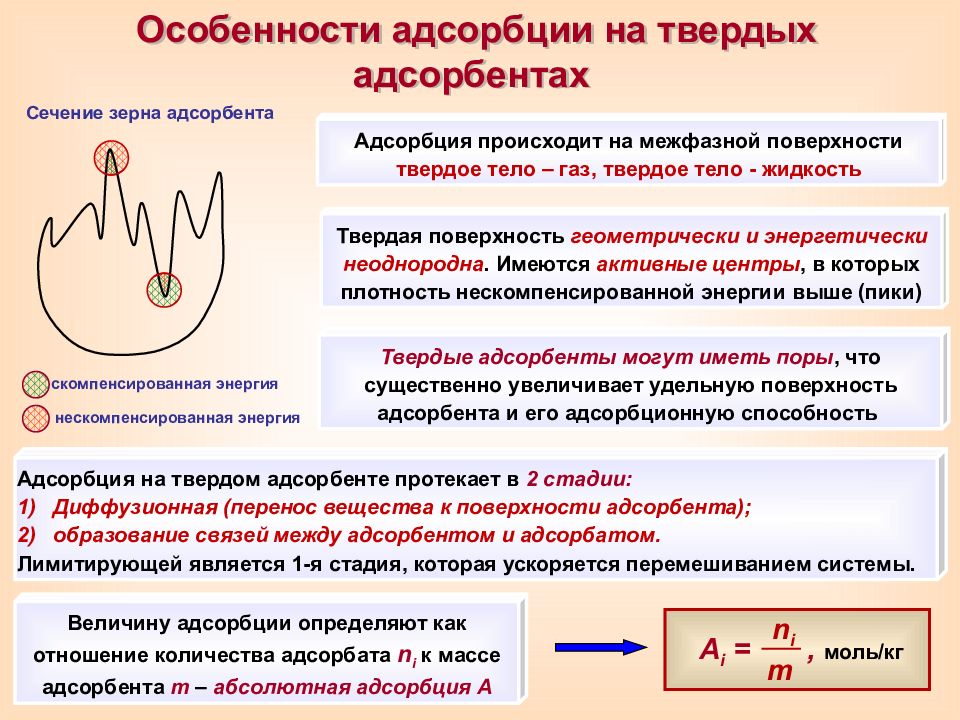
Особенности адсорбции на твердых адсорбентах скомпенсированная энергия нескомпенсированная энергия Адсорбция происходит на межфазной поверхности твердое тело – газ, твердое тело - жидкость Твердая поверхность геометрически и энергетически неоднородна. Имеются активные центры, в которых плотность нескомпенсированной энергии выше (пики) Твердые адсорбенты могут иметь поры, что существенно увеличивает удельную поверхность адсорбента и его адсорбционную способность Сечение зерна адсорбента Адсорбция на твердом адсорбенте протекает в 2 стадии: Диффузионная ( перенос вещества к поверхности адсорбента); образование связей между адсорбентом и адсорбатом. Лимитирующей является 1-я стадия, которая ускоряется перемешиванием системы. A i =, моль/кг n i m Величину адсорбции определяют как отношение количества адсорбата n i к массе адсорбента m – абсолютная адсорбция A
Слайд 35
ТВЕРДЫЕ АДСОРБЕНТЫ В качестве адсорбентов наиболее часто применяют углеродные сорбенты (древесный или костный уголь, графитированная термическая сажа ГТС), бентонитовые глины, силикагель, цеолиты, ионообменные смолы и др. Активированный уголь Силикагель Синтетический цеолит Ионообменная смола
Слайд 36
УГЛЕРОДНЫЕ СОРБЕНТЫ Получают из всевозможного сырья, которое при определенных условиях может давать твердый углеродный остаток – ископаемых углей, торфа, древесины, ореховой скорлупы, фруктовых косточек и животных костей. Лучшими считаются угли, полученные из скорлупы кокосовых орехов и абрикосовых косточек Порошковый уголь Гранулированный уголь Ткань, пропитанная активным углем Экструдированный уголь Формованный уголь Углеродные сорбенты используют в различной форме: в виде порошка с размером частиц до 0,8 мм, гранул более крупного размера, пленок, волокон тканей Углеродные сорбенты до-полнительно активируют, выдерживая при повышен-ной температуре в присут-ствии паров воды и СО 2. При этом выгорает смола, за-полняющая поры углей, удельная поверхность и адсорбционная способность возрастают Удельная поверхность активированного угля, включая поверхность всех его пор, может достигать 1000 м 2 /г.
Слайд 37
Применение углеродных сорбентов Историческая справка Первое упоминание об использовании углей - в сан-скритских писаниях Древней Индии. В них говорилось, что «питьевую воду необходимо предварительно пропускать через уголь, выдерживать в медных сосудах и подвергать действию солнечных лучей». 1773 г. - немецкий химик Карл Шееле сообщил об ад-сорбции газов на древесном угле. 1785 г. - санкт-петербургский аптекарь Ловиц Т. Е., впоследствии ставший академиком, впервые обратил внимание на способность угля очищать спирт. В результате многократных опытов он установил, что даже простое встряхивание вина с угольным порошком позволяет получить намного более чистый и качественный напиток. 1794 г. - активный уголь был использован для осветле-ния сиропов на сахарорафинадном заводе в Англии. 1915 г. -русским ученым Н. Д. Зелинским изобретен первый в мире угольный противогаз. В 1916 г. он был принят на вооружение армий Антанты. Основные сферы применения: очистка воды, пищевых масс; очистка и разделение газов; в хроматографии; в медицине
Слайд 38
СИЛИКАГЕЛЬ Получают высушиванием студня поликремниевой кислоты; по химическому составу – это nSiO 2 Товарный силикагель выпускают в виде зерен или шаровидных гранул размером 0,2 – 7 мм Основные сферы применения: осушка воздуха и промышленных газов; адсорбционная очистка неполярных жидкостей; рекуперации паров органических ве- ществ; в хроматографии – для разделения спиртов, аминокислот, витаминов, антибиотиков и др.; крупнопористые силикагеля – в ка- честве носителей катализаторов Удельная поверхность силикагеля ~ 500 м 2 /г
Слайд 39
ЦЕОЛИТЫ Природные цеолиты Синтетический цеолит Цеолиты (с греч. «кипящий камень» из-за способности вспучиваться при нагревании) – природные и синтетические алюмосиликатные материалы. Кристаллическая структура образована блоками [ SiO 4 ] 4– и [ AlO 4 ] 5–, объединенными общими вершинами в трехмерный каркас, пронизанный полостями и каналами, в которых находятся молекулы воды и катионы металлов I, II групп Цеолиты различных марок имеют строго определенный размер входов в полости и каналы. Поэтому их называют «молекулярными ситами» за способность сорбировать лишь определенные компоненты Основные сферы применения: очистка газов (в т.ч. воздуха), нефти и нефтепродуктов; осушка фреонов ; извлечение радиоактивных элементов
Слайд 40
БЕНТОНИТОВЫЕ ГЛИНЫ Бентониты (от названия месторождения Бентон, США) – тонкодисперсные глины, состоящие на 60-70 % из минералов группы монтмориллонита ( Al 2 O 3 ∙4 SiO 2 ∙ H 2 O ). В зависимости от состава цвет глины может быть желтым, коричневым, серым, зеленым или голубым. Монтмориллонит Глины различных месторождений Основные сферы применения: в пищевой промышленности – для осветления и стабилизации виноматериалов и вин, и частично фруктовых соков, очистки растительных масел; в биотехнологии – для очистки белков, ферментов; в косметологии
Слайд 41
Пористость адсорбентов Тип адсорбентов Диаметр пор, нм Примеры Макропористые более 50 Асбест, мука, древесина Мезопористые 2-50 Бентониты, силикагель Микропористые менее 2 Активированный уголь, цеолиты, пористые стекла Пористые Непористые Твердые адсорбенты П = V п / V адс. Пористость адсорбента определяется отношением суммарного объема пор V п к общему объему адсорбента V адс Классификация пористых адсорбентов Пористость адсорбента имеет большое значение для адсорбции: чем она выше, тем больше удельная поверхность и выше адсорбционная способность. Однако это справедливо только в том случае, если молекулы адсорбата невелики и легко могут проникать в поры
Слайд 42
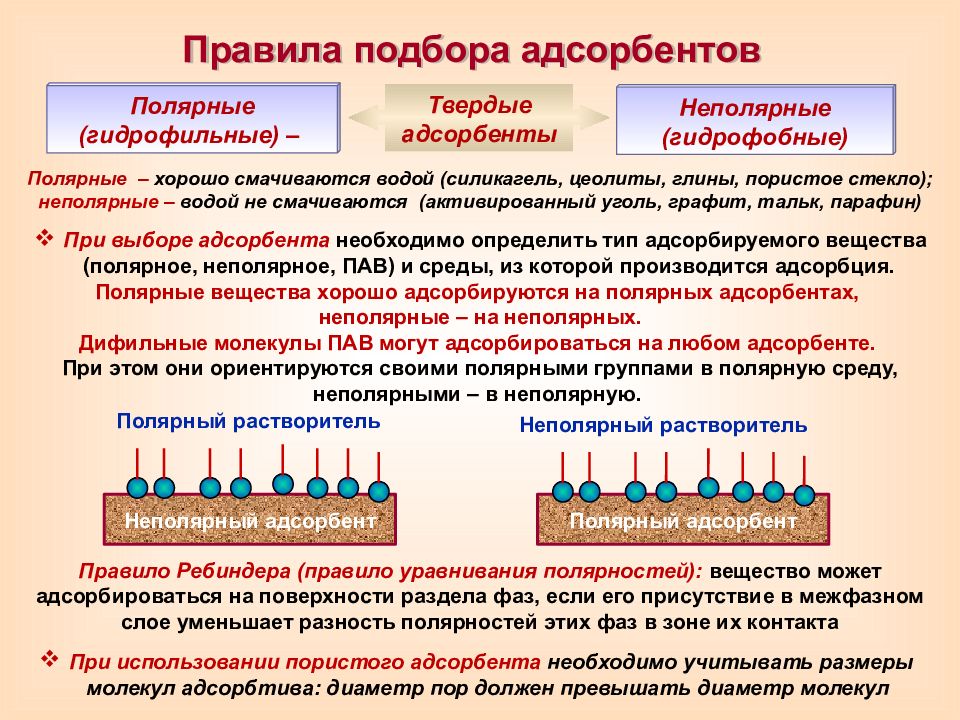
Правила подбора адсорбентов Полярные (гидрофильные) – Неполярные (гидрофобные) Твердые адсорбенты Полярные – хорошо смачиваются водой (силикагель, цеолиты, глины, пористое стекло); неполярные – водой не смачиваются (активированный уголь, графит, тальк, парафин) При выборе адсорбента необходимо определить тип адсорбируемого вещества (полярное, неполярное, ПАВ) и среды, из которой производится адсорбция. Полярные вещества хорошо адсорбируются на полярных адсорбентах, неполярные – на неполярных. Дифильные молекулы ПАВ могут адсорбироваться на любом адсорбенте. При этом они ориентируются своими полярными группами в полярную среду, неполярными – в неполярную. Полярный растворитель Неполярный адсорбент Полярный адсорбент Неполярный растворитель Правило Ребиндера (правило уравнивания полярностей): вещество может адсорбироваться на поверхности раздела фаз, если его присутствие в межфазном слое уменьшает разность полярностей этих фаз в зоне их контакта При использовании пористого адсорбента необходимо учитывать размеры молекул адсорбтива: диаметр пор должен превышать диаметр молекул
Слайд 43
Уравнение Фрейндлиха ln А ln p ln β α tgα = n Графическое определение констант уравнения Фрейндлиха На практике часто для аналитического описания зависимости адсорбции на твердом адсорбенте от концентрации адсорбтива применяется эмпирическое уравнение Фрейндлиха : для адсорбции из растворов для адсорбции газов Преимущество: простота в использовании, поэтому часто применяется в инженерных расчетах Ограничение: можно применять для расчета величины адсорбции в том диапазоне равновесных концентраций, для которого найдены значения констант и n β, n – эмпирические коэффициенты, зависящие от природы адсорбтива и температуры β, n определяют графически. Уравнение Фрейндлиха приводят к линейному виду (логарифмируют левую и правую части): Экспериментальный материал представляют в координатах ln A = f ( ln р ) или ln A = f ( ln с )
Слайд 45
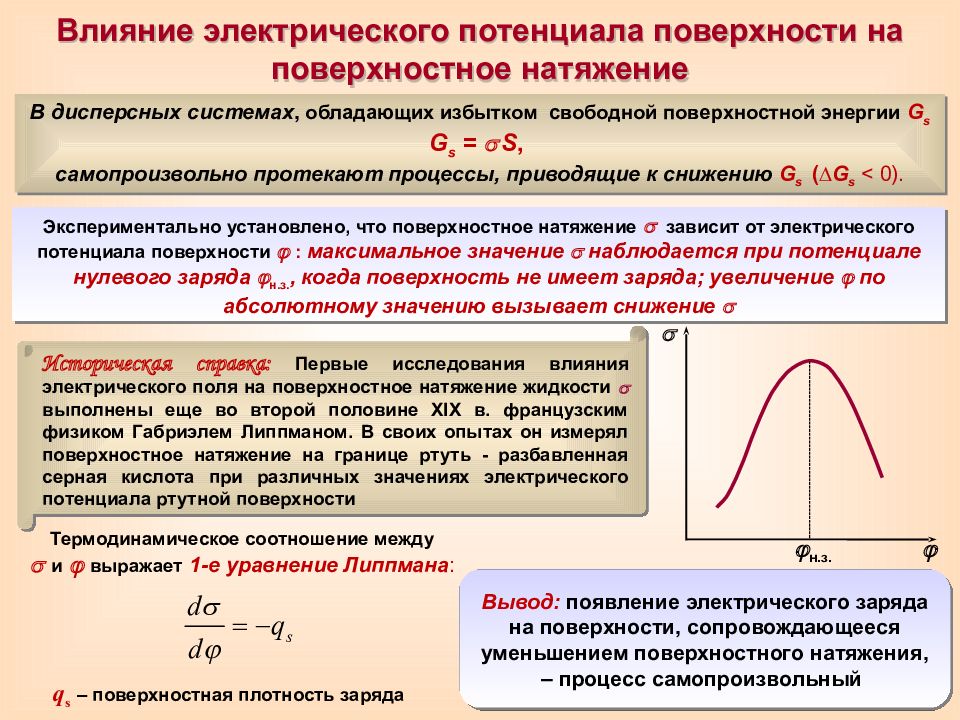
Влияние электрического потенциала поверхности на поверхностное натяжение Термодинамическое соотношение между и выражает 1-е уравнение Липпмана : q s – поверхностная плотность заряда В дисперсных системах, обладающих избытком свободной поверхностной энергии G s G s = S, самопроизвольно протекают процессы, приводящие к снижению G s ( ∆ G s < 0). Экспериментально установлено, что поверхностное натяжение зависит от электрического потенциала поверхности : максимальное значение наблюдается при потенциале нулевого заряда н.з., когда поверхность не имеет заряда; увеличение по абсолютному значению вызывает снижение Историческая справка: Первые исследования влияния электрического поля на поверхностное натяжение жидкости выполнены еще во второй половине XIX в. французским физиком Габриэлем Липпманом. В своих опытах он измерял поверхностное натяжение на границе ртуть - разбавленная серная кислота при различных значениях электрического потенциала ртутной поверхности н.з. Вывод: появление электрического заряда на поверхности, сопровождающееся уменьшением поверхностного натяжения, – процесс самопроизвольный
Слайд 46
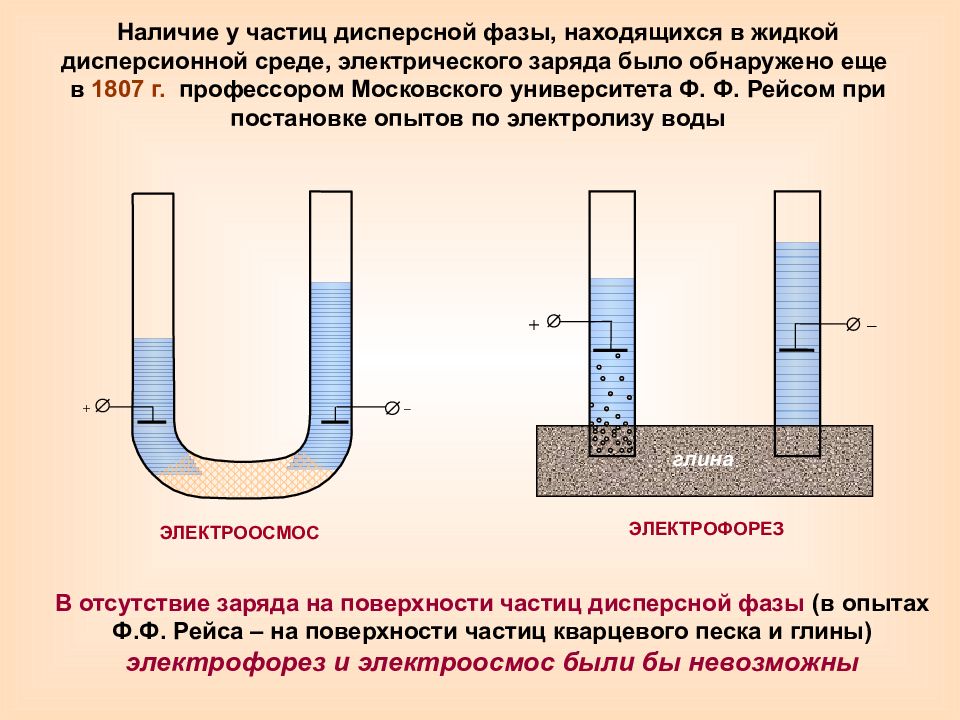
ЭЛЕКТРООСМОС + – Наличие у частиц дисперсной фазы, находящихся в жидкой дисперсионной среде, электрического заряда было обнаружено еще в 1807 г. профессором Московского университета Ф. Ф. Рейсом при постановке опытов по электролизу воды + – глина ЭЛЕКТРОФОРЕЗ В отсутствие заряда на поверхности частиц дисперсной фазы (в опытах Ф.Ф. Рейса – на поверхности частиц кварцевого песка и глины) электрофорез и электроосмос были бы невозможны
Слайд 47
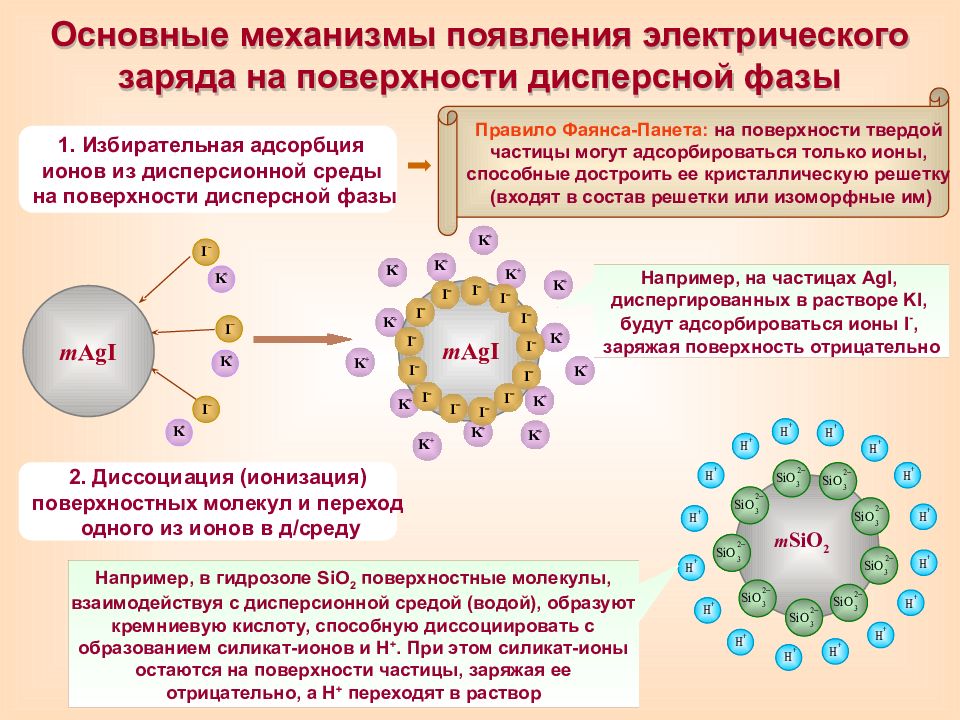
K + K + I – I – I – K + m AgI Основные механизмы появления электрического заряда на поверхности дисперсной фазы Правило Фаянса-Панета: на поверхности твердой частицы могут адсорбироваться только ионы, способные достроить ее кристаллическую решетку (входят в состав решетки или изоморфные им) m SiO 2 1. Избирательная адсорбция ионов из дисперсионной среды на поверхности дисперсной фазы 2. Диссоциация (ионизация) поверхностных молекул и переход одного из ионов в д/среду Например, на частицах AgI, диспергированных в растворе KI, будут адсорбироваться ионы I -, заряжая поверхность отрицательно Например, в гидрозоле SiO 2 поверхностные молекулы, взаимодействуя с дисперсионной средой (водой), образуют кремниевую кислоту, способную диссоциировать с образованием силикат-ионов и Н +. При этом силикат-ионы остаются на поверхности частицы, заряжая ее отрицательно, а Н + переходят в раствор K + K + K + K + K + K + K + K + K + K + K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I –
Слайд 48
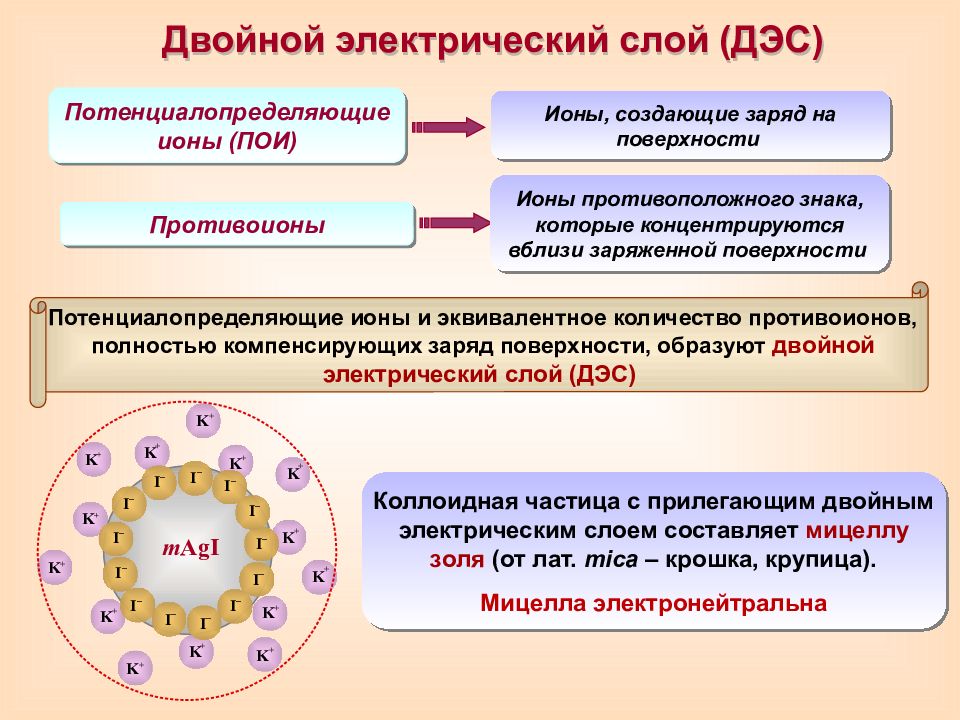
Противоионы Ионы противоположного знака, которые концентрируются вблизи заряженной поверхности Потенциалопределяющие ионы (ПОИ) Ионы, создающие заряд на поверхности Двойной электрический слой (ДЭС) Потенциалопределяющие ионы и эквивалентное количество противоионов, полностью компенсирующих заряд поверхности, образуют двойной электрический слой (ДЭС) K + K + K + K + K + K + K + K + K + K + K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – Коллоидная частица с прилегающим двойным электрическим слоем составляет мицеллу золя (от лат. mica – крошка, крупица). Мицелла электронейтральна
Слайд 49
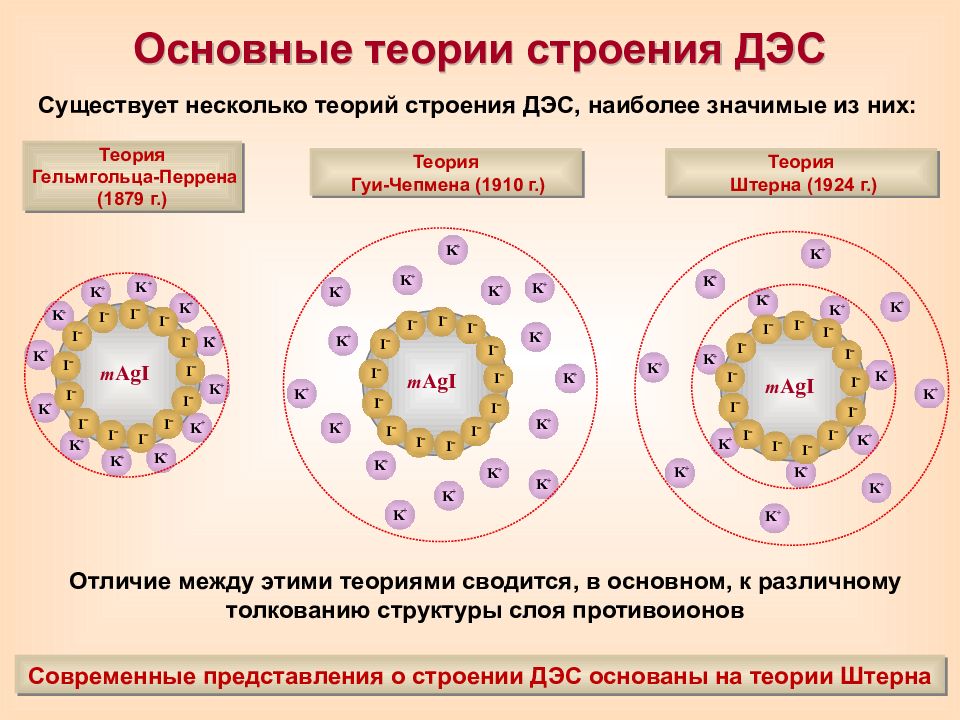
Основные теории строения ДЭС K + K + K + K + K + K + K + K + K + K + K + K + K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – Существует несколько теорий строения ДЭС, наиболее значимые из них: Современные представления о строении ДЭС основаны на теории Штерна Теория Гельмгольца-Перрена (1879 г.) Теория Гуи-Чепмена (1910 г.) Теория Штерна (1924 г.) Отличие между этими теориями сводится, в основном, к различному толкованию структуры слоя противоионов
Слайд 50
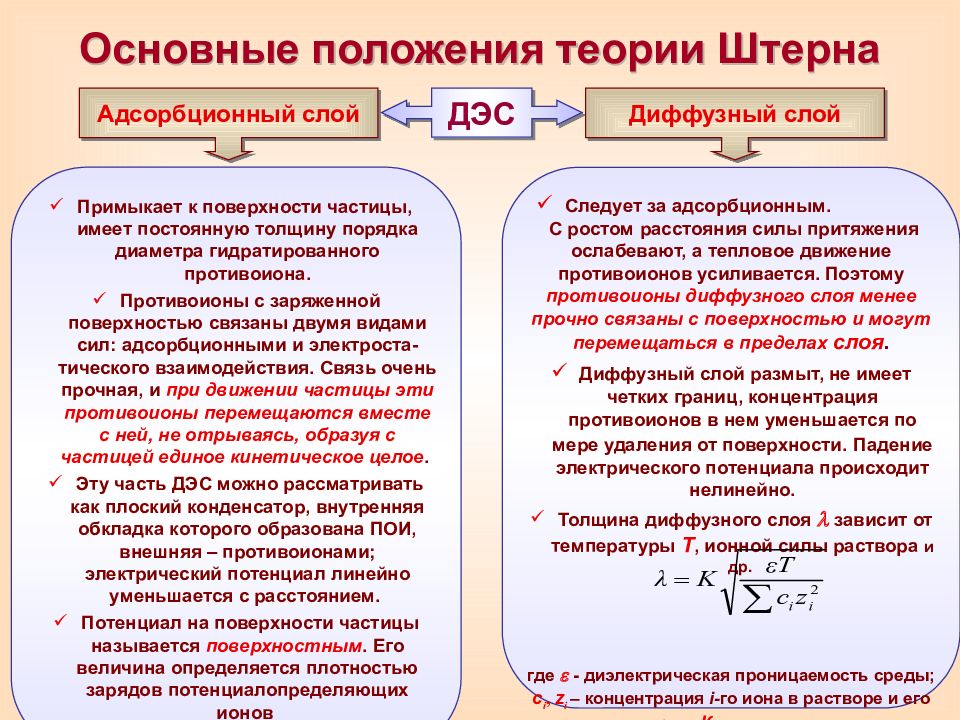
Основные положения теории Штерна Примыкает к поверхности частицы, имеет постоянную толщину порядка диаметра гидратированного противоиона. Противоионы с заряженной поверхностью связаны двумя видами сил: адсорбционными и электроста-тического взаимодействия. Связь очень прочная, и при движении частицы эти противоионы перемещаются вместе с ней, не отрываясь, образуя с частицей единое кинетическое целое. Эту часть ДЭС можно рассматривать как плоский конденсатор, внутренняя обкладка которого образована ПОИ, внешняя – противоионами; электрический потенциал линейно уменьшается с расстоянием. Потенциал на поверхности частицы называется поверхностным. Его величина определяется плотностью зарядов потенциалопределяющих ионов Адсорбционный слой ДЭС Диффузный слой Следует за адсорбционным. С ростом расстояния силы притяжения ослабевают, а тепловое движение противоионов усиливается. Поэтому противоионы диффузного слоя менее прочно связаны с поверхностью и могут перемещаться в пределах слоя. Диффузный слой размыт, не имеет четких границ, концентрация противоионов в нем уменьшается по мере удаления от поверхности. Падение электрического потенциала происходит нелинейно. Толщина диффузного слоя зависит от температуры Т, ионной силы раствора и др. где - диэлектрическая проницаемость среды; с i, z i – концентрация i - го иона в растворе и его заряд; К – константа
Слайд 51
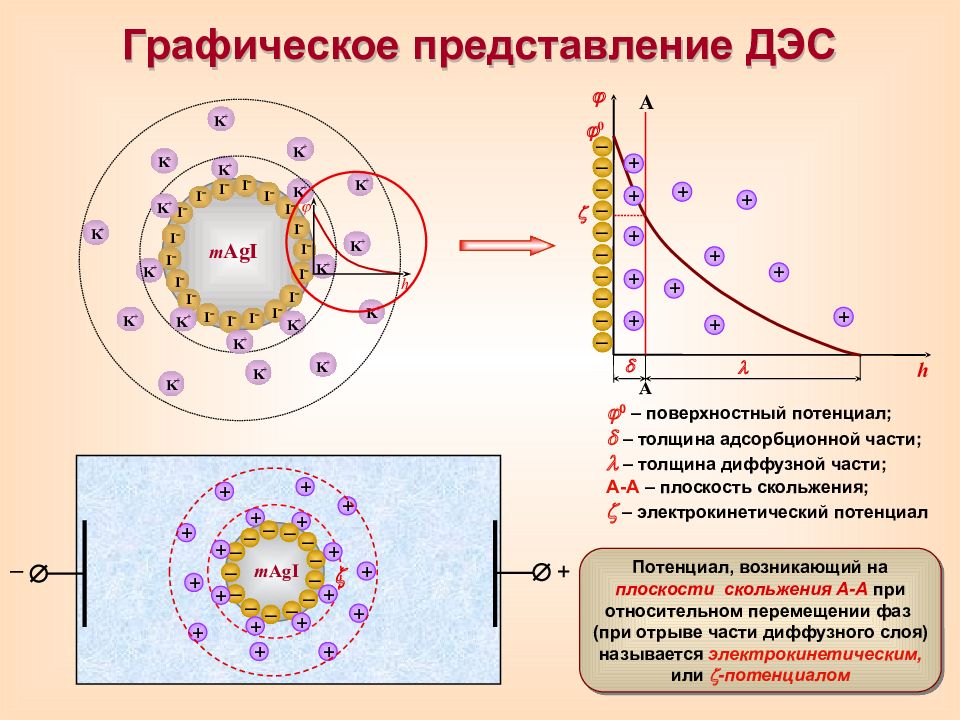
Графическое представление ДЭС 0 – поверхностный потенциал; – толщина адсорбционной части; – толщина диффузной части; А-А – плоскость скольжения; – электрокинетический потенциал h – + + + + + + + + + + + + + m AgI – – – – – – – – – – – – – + + + + + + 0 h А А + + + + + + + + + + + + – – – – – – – – – – Потенциал, возникающий на плоскости скольжения А-А при относительном перемещении фаз (при отрыве части диффузного слоя) называется электрокинетическим, или -потенциалом K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K + K + I – I – I – I – I – I – K + K + K +
Слайд 52
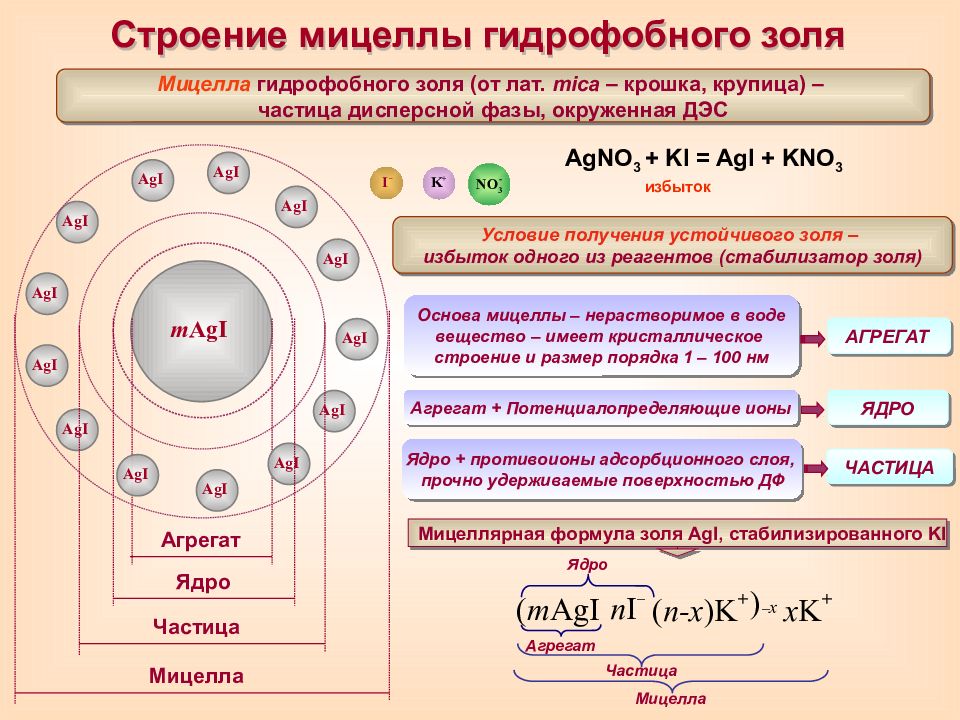
m AgI Агрегат AgI AgI AgI AgI AgI AgI AgI AgI AgI AgI AgI AgI AgI I – K + NO 3 - I – I – I – I – I – I – I – I – I – I – I – I – I – Ядро Мицелла гидрофобного золя (от лат. mica – крошка, крупица) – частица дисперсной фазы, окруженная ДЭС АГРЕГАТ Основа мицеллы – нерастворимое в воде вещество – имеет кристаллическое строение и размер порядка 1 – 100 нм Условие получения устойчивого золя – избыток одного из реагентов (стабилизатор золя) Мицеллярная формула золя А gI, стабилизированного KI K + K + K + K + K + K + K + K + Строение мицеллы гидрофобного золя Частица K + K + K + K + K + K + K + K + K + K + K + K + Мицелла AgNO 3 + KI = AgI + KNO 3 избыток ЯДРО Агрегат + Потенциалопределяющие ионы ЧАСТИЦА Ядро + противоионы адсорбционного слоя, прочно удерживаемые поверхностью ДФ m AgI Агрегат n I – Ядро x K + ( n-x )K + Частица ( ) – x Мицелла
Слайд 54
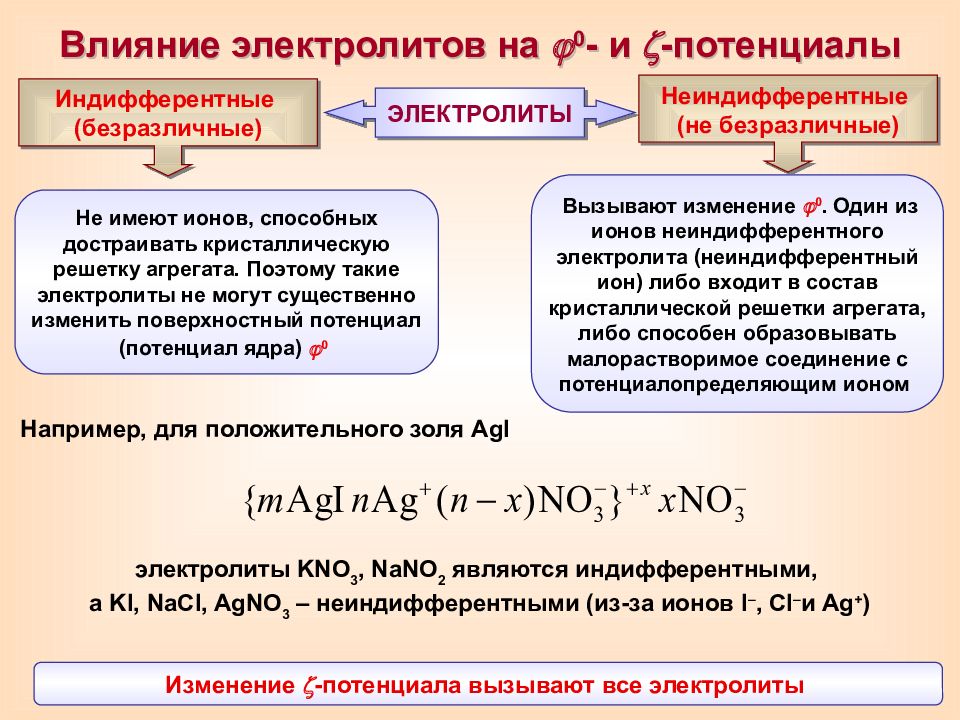
Влияние электролитов на 0 - и -потенциалы Не имеют ионов, способных достраивать кристаллическую решетку агрегата. Поэтому такие электролиты не могут существенно изменить поверхностный потенциал (потенциал ядра) 0 Индифферентные (безразличные) ЭЛЕКТРОЛИТЫ Неиндифферентные (не безразличные) Вызывают изменение 0. Один из ионов неиндифферентного электролита (неиндифферентный ион) либо входит в состав кристаллической решетки агрегата, либо способен образовывать малорастворимое соединение с потенциалопределяющим ионом Изменение -потенциала вызывают все электролиты Например, для положительного золя AgI электролиты KNO 3, NaNO 2 являются индифферентными, а KI, NaCl, AgNO 3 – неиндифферентными (из-за ионов I –, Cl – и Ag + )
Слайд 55
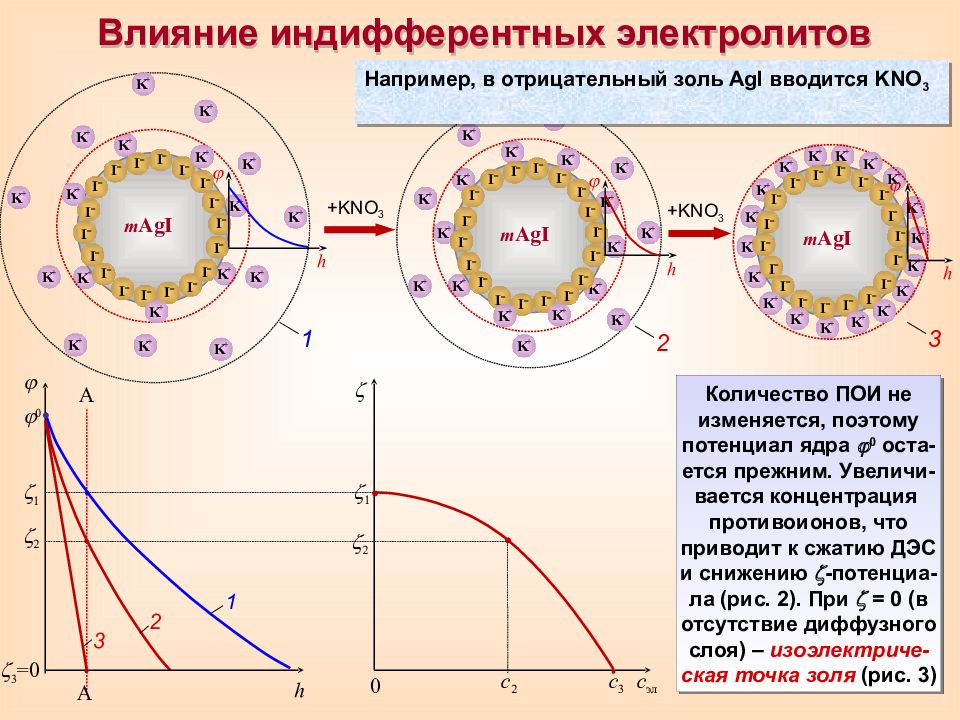
Влияние индифферентных электролитов 1 2 3 =0 h 0 А А 1 2 3 с эл 0 с 2 с 3 1 2 K + K + K + K + K + K + K + K + K + K + K + K + K + h m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + h m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K + 1 K + K + K + K + K + K + K + h m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + 2 3 Количество ПОИ не изменяется, поэтому потенциал ядра 0 оста-ется прежним. Увеличи-вается концентрация противоионов, что приводит к сжатию ДЭС и снижению - потенциа-ла (рис. 2). При = 0 (в отсутствие диффузного слоя) – изоэлектриче-ская точка золя (рис. 3) + KNO 3 + KNO 3 Например, в отрицательный золь AgI вводится KNO 3
Слайд 56
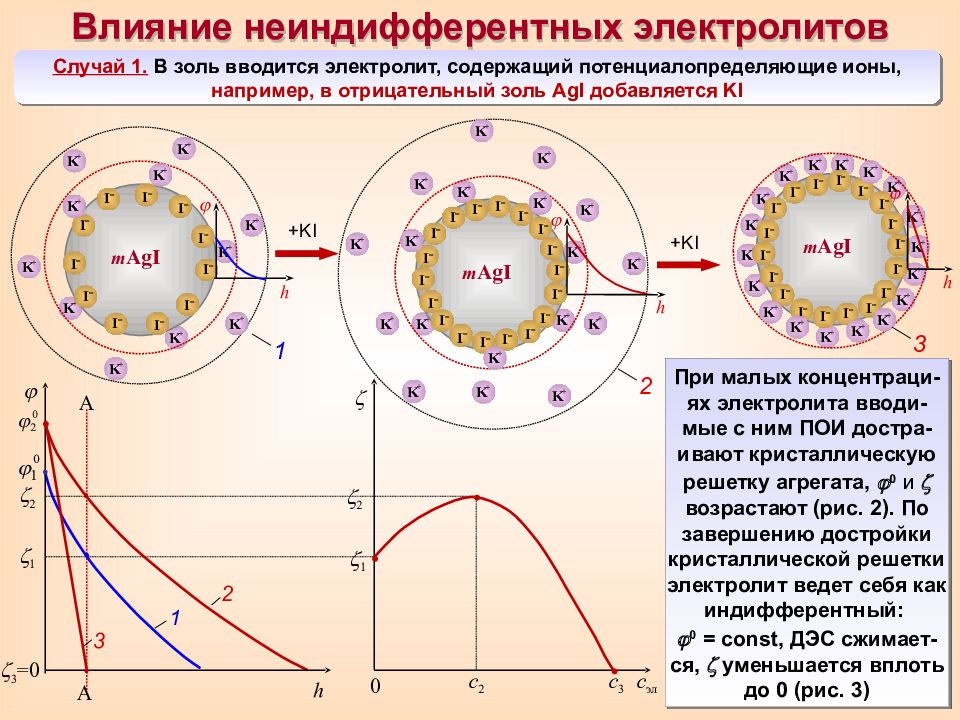
Влияние неиндифферентных электролитов Случай 1. В золь вводится электролит, содержащий потенциалопределяющие ионы, например, в отрицательный золь AgI добавляется KI K + K + K + h m AgI I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + 1 1 2 3 =0 h А А 1 2 3 с эл 0 с 2 с 3 1 2 + KI K + K + K + K + h m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K + 2 + KI K + K + K + K + K + K + K + K + K + K + K + K + K + h m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + 3 При малых концентраци-ях электролита вводи-мые с ним ПОИ достра-ивают кристаллическую решетку агрегата, 0 и возрастают (рис. 2). По завершению достройки кристаллической решетки электролит ведет себя как индифферентный: 0 = const, ДЭС сжимает - ся, уменьшается вплоть до 0 (рис. 3)
Слайд 57
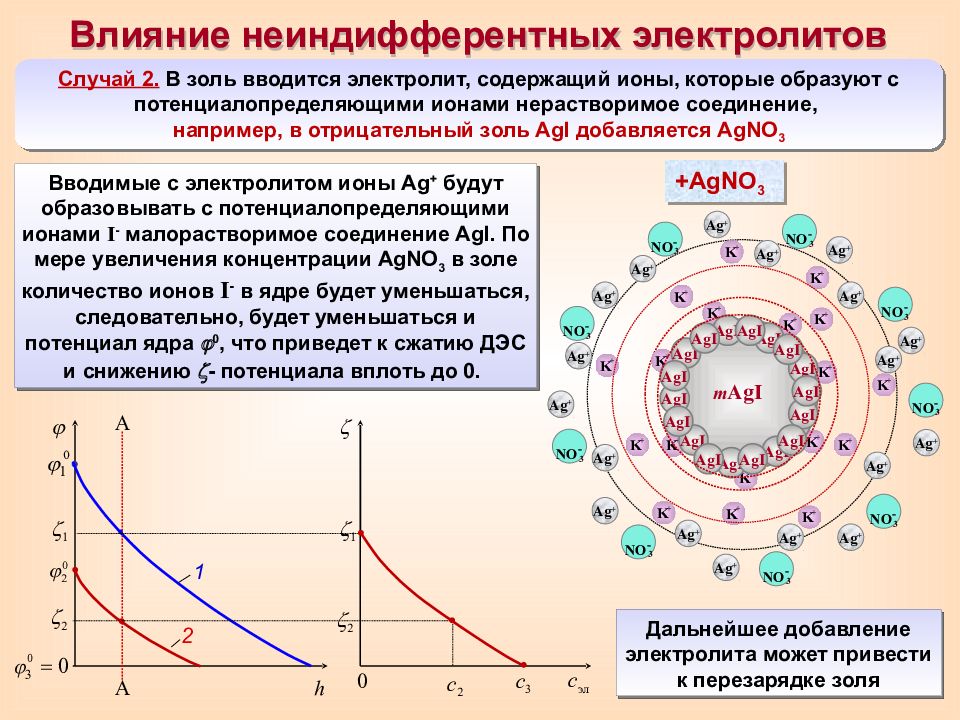
Влияние неиндифферентных электролитов Случай 2. В золь вводится электролит, содержащий ионы, которые образуют с потенциалопределяющими ионами нерастворимое соединение, например, в отрицательный золь AgI добавляется AgNO 3 K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K + +AgNO 3 Ag + Ag + Ag + Ag + Ag + Ag + NO - 3 Ag + NO - 3 NO - 3 NO - 3 NO - 3 NO - 3 NO - 3 NO - 3 NO - 3 Ag + Ag + h А А 1 1 с эл 1 AgI AgI AgI AgI AgI AgI AgI AgI AgI 2 2 с 2 Ag + Ag + Ag + Ag + Ag + Ag + Ag + Ag + Ag + AgI AgI AgI AgI AgI AgI AgI AgI AgI 0 с 3 Вводимые с электролитом ионы Ag + будут образовывать с потенциалопределяющими ионами I - малорастворимое соединение AgI. По мере увеличения концентрации AgNO 3 в золе количество ионов I - в ядре будет уменьшаться, следовательно, будет уменьшаться и потенциал ядра 0, что приведет к сжатию ДЭС и снижению - потенциала вплоть до 0. Дальнейшее добавление электролита может привести к перезарядке золя 2
Слайд 58
ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ Электрокинетические явления – это явления, которые возникают при воздействии электрического поля на дисперсную систему (электрофорез, электроосмос) или в результате перемещения частиц дисперсной фазы или дисперсионной среды (потенциалы течения и оседания). Все электрокинетические явления обусловлены наличием ДЭС на межфазной поверхности, интенсивность их определяется величиной - потенциала
Слайд 59
Электрофорез Электрофорез – направленное движение частиц дисперсной фазы относительно дисперсионной среды под действием внешнего электрического поля При наложении внешнего электрического поля происходит разрыв мицеллы по плоскости скольжения: коллоидная частица перемеща-ется к одному электроду, а противоионы диффузного слоя, энер-гетически менее прочно связанные с поверхностью, – к другому Электрофоретическая скорость Е – напряженность (градиент) внешнего электрического поля; - динамическая вязкость; , 0 – диэлектрическая проницаемость среды и электрическая проницаемость; - фактор формы (для сферы = 0,66) Электрофоретический эффект: под действием электрического поля противоионы передвигаются в направлении, противоположном движению частицы. За счет гидратации они увле-кают за собой и окружающую их жидкость, созда-вая противоток движению частицы Релаксационный эффект: вследствие движения фаз в противоположных направлениях симметрия диффузной части ДЭС нарушается. Возникает добавочное электрическое поле, направленное против внешнего и стремя-щееся двигать частицу в обратном направлении – + + + + + + + + + + + + + m AgI – – – – – – – – – – – – – + + + + + +
Слайд 60
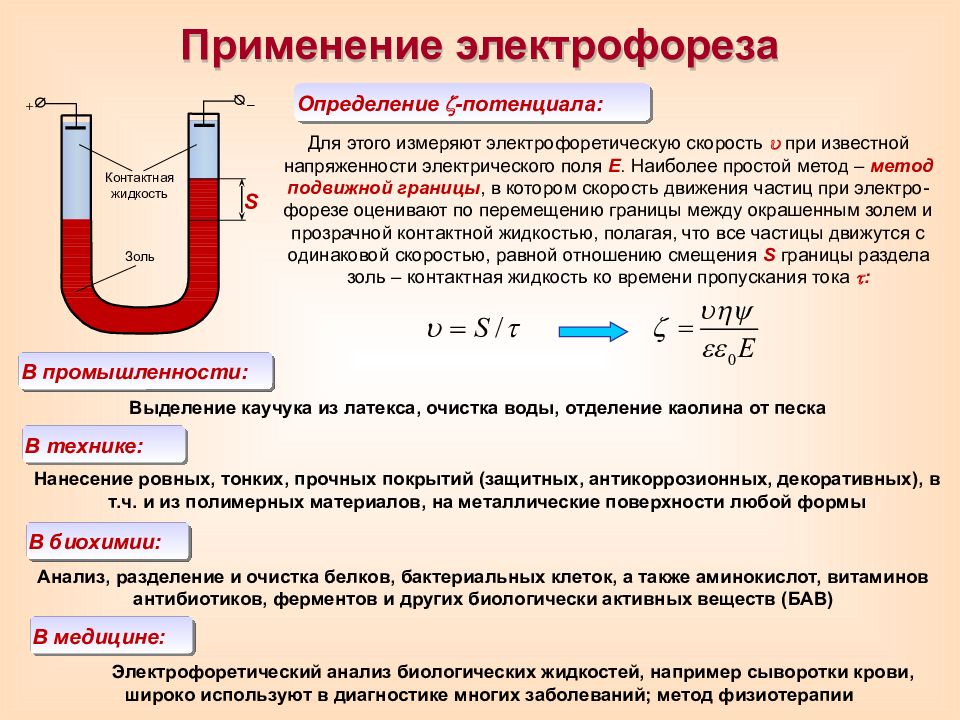
Применение электрофореза + – Для этого измеряют электрофоретическую скорость при известной напряженности электрического поля Е. Наиболее простой метод – метод подвижной границы, в котором скорость движения частиц при электро-форезе оценивают по перемещению границы между окрашенным золем и прозрачной контактной жидкостью, полагая, что все частицы движутся с одинаковой скоростью, равной отношению смещения S границы раздела золь – контактная жидкость ко времени пропускания тока : Определение -потенциала: S Контактная жидкость Золь В промышленности: Выделение каучука из латекса, очистка воды, отделение каолина от песка Электрофоретический анализ биологических жидкостей, например сыворотки крови, широко используют в диагностике многих заболеваний; метод физиотерапии В технике: Нанесение ровных, тонких, прочных покрытий (защитных, антикоррозионных, декоративных), в т.ч. и из полимерных материалов, на металлические поверхности любой формы В биохимии: Анализ, разделение и очистка белков, бактериальных клеток, а также аминокислот, витаминов антибиотиков, ферментов и других биологически активных веществ (БАВ) В медицине:
Слайд 61
Электроосмос + – Капиллярно-пористое тело Движение противоионов в капилляре – + – – – – – – – – – – – – – – – – – – – – + + + + + + + + + + + + + + + + + + Электроосмос – движение дисперсионной среды через неподвижную капиллярно-пористую перегородку под действием внешнего электрического поля Электроосмотический перенос жидкости происходит в капиллярно-пористых системах и обусловлен наличием ДЭС на внутренней поверхности капилляров пористого тела. Рассмотрим сечение отдельного капилляра, например, кварцевого, поверхность которого заряжена отрицательно. Пленка жидкости вместе с противоионами адсорбционного слоя «прилипает» к стенке капилляра и остается неподвижной, а противоионы диффузной части ДЭС, слабо связанные с поверхностью, под действием внешнего электрического поля перемещаются к противоположно заряженному электроду. Противоионы гидратированы, поэтому они увлекают за собой и окружающую их жидкость. Применение электроосмоса: 1. Определение -потенциала на поверхности капиллярно-пористых тел. 2. Удаление избыточной влаги из почв при прокладке транспортных магистралей и гидротехническом строительстве, обезвоживания древесины и пористых материалов, осушки зданий, понижения уровня грунтовых вод
Слайд 62
Потенциал течения Капиллярно-пористое тело р Потенциал течения (эффект Квинке) – возникновение разности потенциалов при протекании жидкости, находящейся под давлением, через неподвижную капиллярно-пористую перегородку При течении жидкости по капиллярам под действием разности давлений за нею увлекаются противоионы диффузного слоя. На концах капилляра возникает разность потенциалов, которая, в свою очередь, вызывает встречный объемный поток ионов противоположного знака. По разные стороны от капиллярно-пористой перегородки будут накапливаться ионы противоположного знака. При установившемся равновесии потоки ионов станут равными, а разность потенциалов примет постоянное значение, равное потенциалу течения. Движение противоионов в капилляре – – – – – – – – – – – – – – – – – – – – + + + + + + + + + + + + + + + + + + Потенциалы течения возникают, например, при движении подземных вод через грунт и горные породы и могут служить источником информации для геологов и геофизиков, при циркуляции крови по капиллярам кровеносной системы, являясь одним из источников биопотенциалов в организме, перекачке технологических растворов и жидкого топлива по трубопроводам. При транспортировке жидкого топлива возникающие потенциалы течения могут стать причиной пожаров и взрывов. Например, при перекачке нефти потенциал течения может достигать сотен вольт. р
Слайд 63
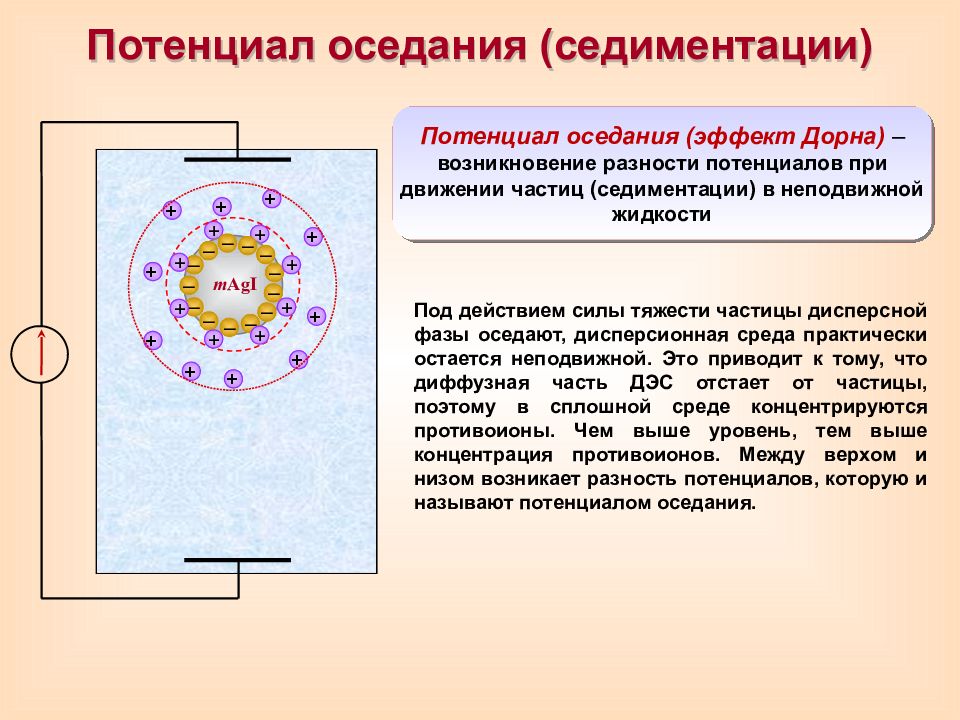
Потенциал оседания (седиментации) + + + + + + + + + + + + m AgI – – – – – – – – – – – – – + + + + + + Потенциал оседания (эффект Дорна) – возникновение разности потенциалов при движении частиц (седиментации) в неподвижной жидкости Под действием силы тяжести частицы дисперсной фазы оседают, дисперсионная среда практически остается неподвижной. Это приводит к тому, что диффузная часть ДЭС отстает от частицы, поэтому в сплошной среде концентрируются противоионы. Чем выше уровень, тем выше концентрация противоионов. Между верхом и низом возникает разность потенциалов, которую и называют потенциалом оседания.
Слайд 65
Лиофобные дисперсные системы термодинамически неустойчивы. Для них характерно протекание процессов, приводящих к их разрушению, вплоть до разделения на макрофазы. Эмульсия Масло Вода Например, эмульсия без эмульгатора разрушается в течение нескольких секунд с момента ее образования. Поэтому можно говорить только об относительной устойчивости, под которой понимается способность дисперсной системы сохранять неизменными во времени численную концентрацию частиц дисперсной фазы и их распределение по объему системы На практике, часто приходится решать две противоположные задачи - сохранить дисперсную систему или разрушить ее. Например, устойчивыми должны быть дисперсные пищевые системы; очистка воды природных водоемов от примесей связана с разрушением дисперсной системы. Различают 2 вида устойчивости – седиментационную и агрегативную Проблема устойчивости дисперсных систем – одна из центральных проблем коллоидной химии
Слайд 66
Седиментационная устойчивость дисперсных систем Седиментационная устойчивость – это способность дисперсной системы противодействовать оседанию частиц Седиментация (оседание) происходит под действием силы тяжести F т : F т = mg = Vg, где m, , V – масса, плотность и объем частицы; g – ускорение свободного падения Противодействие силе тяжести зависит от размеров частиц. Для относи-тельно крупных частиц (средне- и грубодисперсные системы) – это архи-медова сила F А и сила трения F тр, для частиц коллоидных размеров – броуновское движение, следствием которого является их диффузия, стремящаяся выровнять концентрацию частиц по всему объему. Сила трения пропорциональна вязкости дисперсионной среды : F тр , а интенсивность броуновского движения – температуре Т : F диф Т
Слайд 67
Для повышения седиментационной устойчивости необходимо: уменьшить силу тяжести за счет уменьшения размера частиц с помощью специальных устройств – коллоидных мельниц, гомогенизаторов и др. увеличить вязкость среды введением спе - циальных добавок (сиропов, ВМС) обеспечить хранение дисперсной системы при температуре, не ниже установленной нормы Для нарушения седиментационной устойчивости необходимо: увеличить силу тяжести, например, применением центробежного поля (сепарирование, центрифугирование). Так, при сепарировании молока эмульсия разрушается и выделяется молочный жир, капельки которого являются дисперсной фазой
Слайд 68
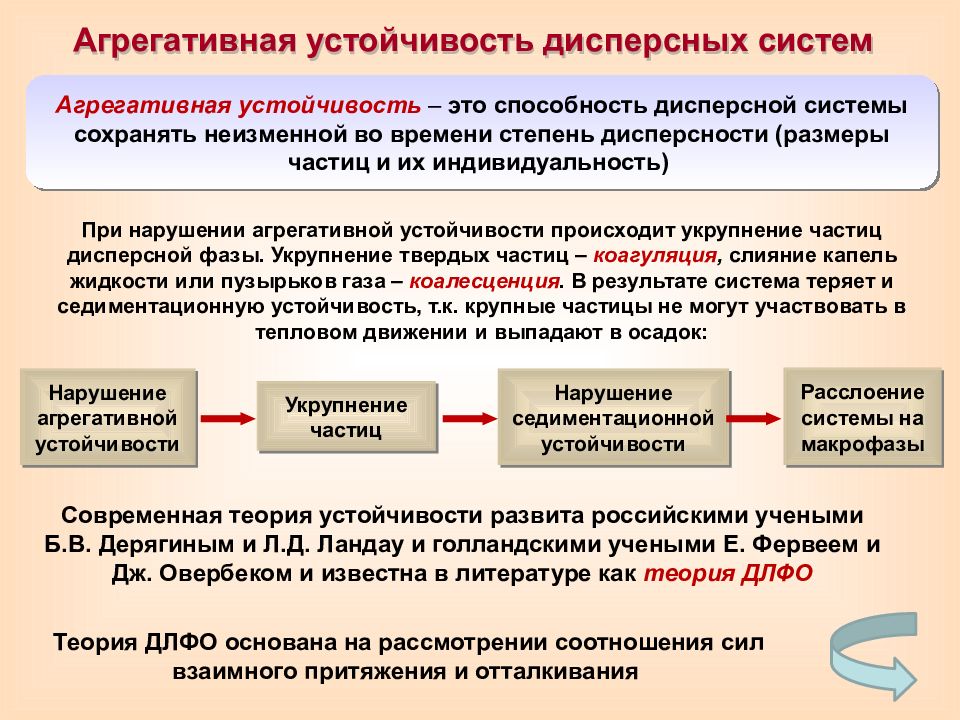
Агрегативная устойчивость дисперсных систем Агрегативная устойчивость – это способность дисперсной системы сохранять неизменной во времени степень дисперсности (размеры частиц и их индивидуальность) Нарушение агрегативной устойчивости Нарушение седиментационной устойчивости Укрупнение частиц Расслоение системы на макрофазы Современная теория устойчивости развита российскими учеными Б.В. Дерягиным и Л.Д. Ландау и голландскими учеными Е. Фервеем и Дж. Овербеком и известна в литературе как теория ДЛФО Теория ДЛФО основана на рассмотрении соотношения сил взаимного притяжения и отталкивания При нарушении агрегативной устойчивости происходит укрупнение частиц дисперсной фазы. Укрупнение твердых частиц – коагуляция, слияние капель жидкости или пузырьков газа – коалесценция. В результате система теряет и седиментационную устойчивость, т.к. крупные частицы не могут участвовать в тепловом движении и выпадают в осадок:
Слайд 69
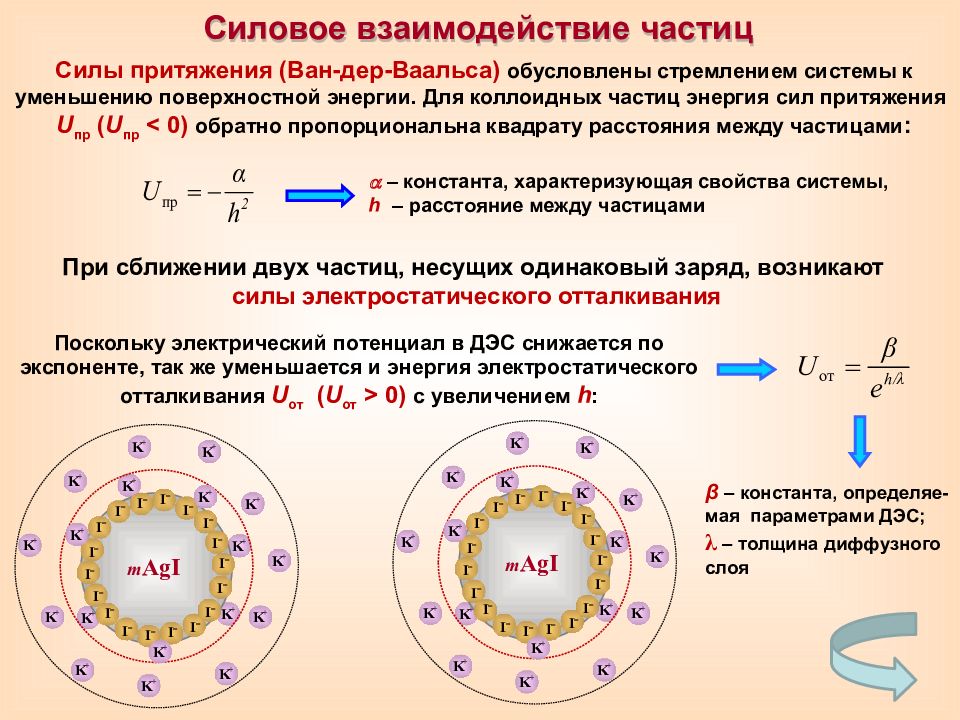
Силовое взаимодействие частиц K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K + Силы притяжения (Ван-дер-Ваальса) обусловлены стремлением системы к уменьшению поверхностной энергии. Для коллоидных частиц энергия сил притяжения U пр ( U пр < 0) обратно пропорциональна квадрату расстояния между частицами : – константа, характеризующая свойства системы, h – расстояние между частицами При сближении двух частиц, несущих одинаковый заряд, возникают силы электростатического отталкивания Поскольку электрический потенциал в ДЭС снижается по экспоненте, так же уменьшается и энергия электростатического отталкивания U от ( U от > 0) с увеличением h : β – константа, определяе-мая параметрами ДЭС; λ – толщина диффузного слоя K + K + K + K + m AgI I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – I – K + K + K + K + K + K + K + K + K + K + K + K + K + K +
Слайд 70
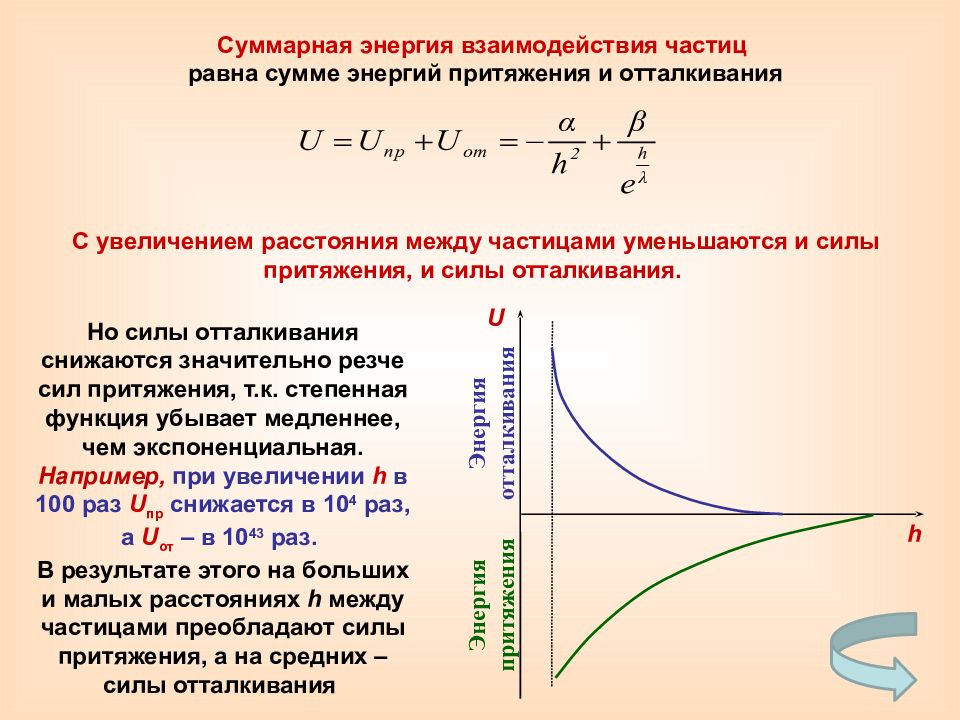
Суммарная энергия взаимодействия частиц равна сумме энергий притяжения и отталкивания Энергия отталкивания Энергия притяжения h U Но силы отталкивания снижаются значительно резче сил притяжения, т.к. степенная функция убывает медленнее, чем экспоненциальная. Например, при увеличении h в 100 раз U пр снижается в 10 4 раз, а U от – в 10 43 раз. В результате этого на больших и малых расстояниях h между частицами преобладают силы притяжения, а на средних – силы отталкивания С увеличением расстояния между частицами уменьшаются и силы притяжения, и силы отталкивания.
Слайд 71
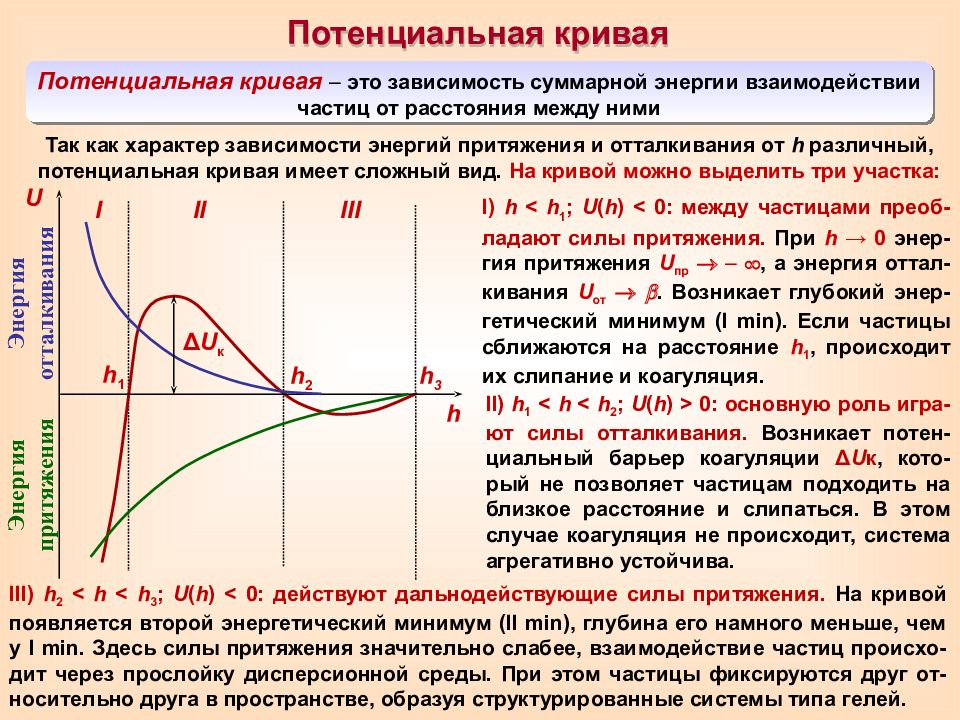
I III h 1 h 2 h 3 Δ U к II Потенциальная кривая Потенциальная кривая – это зависимость суммарной энергии взаимодействии частиц от расстояния между ними Энергия отталкивания Энергия притяжения h U Так как характер зависимости энергий притяжения и отталкивания от h различный, потенциальная кривая имеет сложный вид. На кривой можно выделить три участка: I ) h < h 1 ; U ( h ) < 0: между частицами преоб-ладают силы притяжения. При h → 0 энер-гия притяжения U пр – , а энергия оттал-кивания U от . Возникает глубокий энер-гетический минимум ( I min). Если частицы сближаются на расстояние h 1, происходит их слипание и коагуляция. II) h 1 < h < h 2 ; U ( h ) > 0: основную роль игра - ют силы отталкивания. Возникает потен - циальный барьер коагуляции Δ U к, кото - рый не позволяет частицам подходить на близкое расстояние и слипаться. В этом случае коагуляция не происходит, система агрегативно устойчива. III ) h 2 < h < h 3 ; U ( h ) < 0: действуют дальнодействующие силы притяжения. На кривой появляется второй энергетический минимум ( II min ), глубина его намного меньше, чем у I min. Здесь силы притяжения значительно слабее, взаимодействие частиц происхо-дит через прослойку дисперсионной среды. При этом частицы фиксируются друг от-носительно друга в пространстве, образуя структурированные системы типа гелей.
Слайд 72
Если кинетическая энергия частиц мала, то при достаточно глубоком II min они фиксируются друг относительно друга на некотором расстоянии, образуя структурированные системы. Если глубина II min невелика, а потенциальный барьер коагуля - ции высокий, частицы не могут сблизиться на критические рас- стояния, так как действуют мощные силы отталкивания. Система агрегативно устойчива. Если частицы обладают высокой кинетической энергией, то при небольших II min и потенциальном барьере частицы слипаются, происходит коагуляция. Выводы: Таким образом, чтобы началась коагуляция, частицы должны преодолеть потенциальный барьер, высота которого определяется величиной -потенциала
Слайд 73
Факторы, определяющие агрегативную устойчивость 1. Адсорбционно-сольватный фактор – наличие двойного электрического слоя на поверхности частиц и достаточно высокого значения -потенциала, которое обеспечивается дополнительной адсорбцией ионов, повышающих поверхностный потенциал 0, либо снижением концентрации противоионов, например, очисткой золя. 2. Структурно-механический фактор – образование защитного трехмерного адсорбционного слоя на поверхности частиц при добавлении в систему стабилизаторов – ВМС или коллоидных ПАВ. При этом важно правильно подобрать концентрацию вводимого стабили-затора. При его недостатке возможно образование флокул, в которых частицы связаны друг с другом мостиками из полимерных цепей. Такой процесс называют флокуляцией (от лат. flocculi – клочья, хлопья), а вещества, его вызывающие – флокулянтами Образование флокул
Слайд 74
Коагуляция лиофобных золей Коагуляция – процесс слипания частиц дисперсной фазы с образованием крупных агрегатов (от лат. coagulation – свертывание, сгущение) Коагуляция сопровождается уменьшением межфазной поверхности, а, следовательно, и свободной поверхностной энергии G s. Система переходит в более устойчивое состояние. Для начала коагуляции частицы должны преодолеть потенциальный барьер Δ U к и сблизиться на критические расстояния – попасть в I энергетический минимум потенциальной кривой, что возможно при снижении электрокинетического потенциала. Коагуляция может происходить под действием различных факторов в зависимости от способа стабилизации системы, например, воздействием ультразвуком, электрическим полем, высокими и низкими температурами. Наиболее часто коагуляцию вызывают добавлением электролитов – это электролитная коагуляция.
Слайд 75
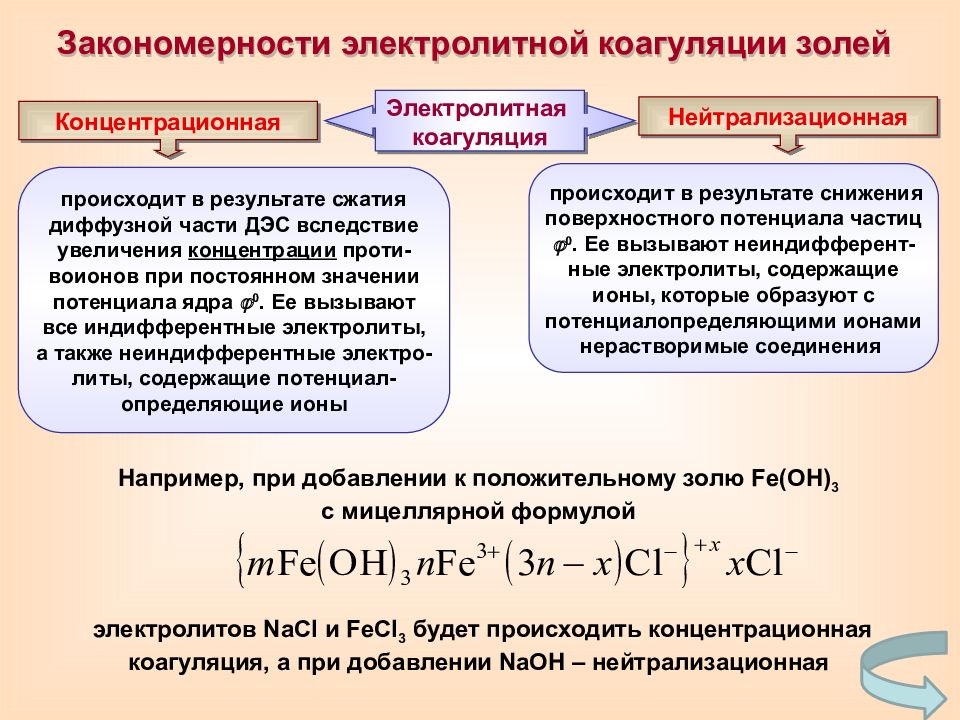
Закономерности электролитной коагуляции золей происходит в результате сжатия диффузной части ДЭС вследствие увеличения концентрации проти-воионов при постоянном значении потенциала ядра 0. Ее вызывают все индифферентные электролиты, а также неиндифферентные электро-литы, содержащие потенциал-определяющие ионы Концентрационная Электролитная коагуляция Нейтрализационная происходит в результате снижения поверхностного потенциала частиц 0. Ее вызывают неиндифферент-ные электролиты, содержащие ионы, которые образуют с потенциалопределяющими ионами нерастворимые соединения Например, при добавлении к положительному золю Fe(OH) 3 с мицеллярной формулой электролитов NaCl и FeCl 3 будет происходить концентрационная коагуляция, а при добавлении NaOH – нейтрализационная
Слайд 77
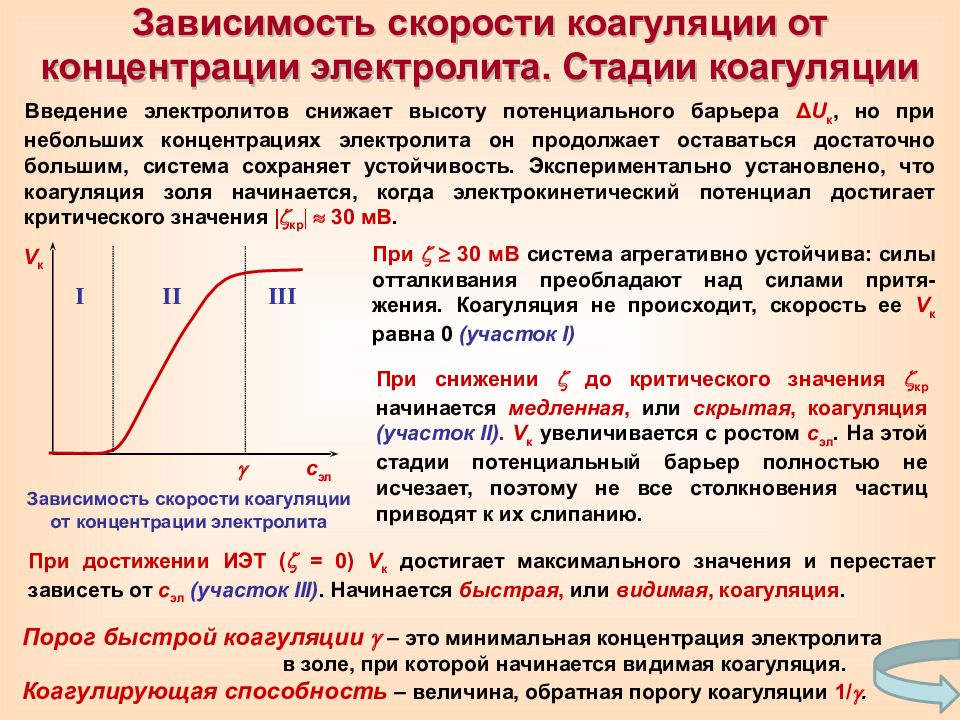
V к I II III с эл Зависимость скорости коагуляции от концентрации электролита Введение электролитов снижает высоту потенциального барьера Δ U к, но при небольших концентрациях электролита он продолжает оставаться достаточно большим, система сохраняет устойчивость. Экспериментально установлено, что коагуляция золя начинается, когда электрокинетический потенциал достигает критического значения кр 30 мВ. Зависимость скорости коагуляции от концентрации электролита. Стадии коагуляции При 30 мВ система агрегативно устойчива: силы отталкивания преобладают над силами притя-жения. Коагуляция не происходит, скорость ее V к равна 0 (участок I ) При снижении до критического значения кр начинается медленная, или скрытая, коагуляция (участок II ). V к увеличивается с ростом с эл. На этой стадии потенциальный барьер полностью не исчезает, поэтому не все столкновения частиц приводят к их слипанию. При достижении ИЭТ ( = 0) V к достигает максимального значения и перестает зависеть от с эл (участок III ). Начинается быстрая, или видимая, коагуляция. Порог быстрой коагуляции – это минимальная концентрация электролита в золе, при которой начинается видимая коагуляция. Коагулирующая способность – величина, обратная порогу коагуляции 1/ .
Слайд 78
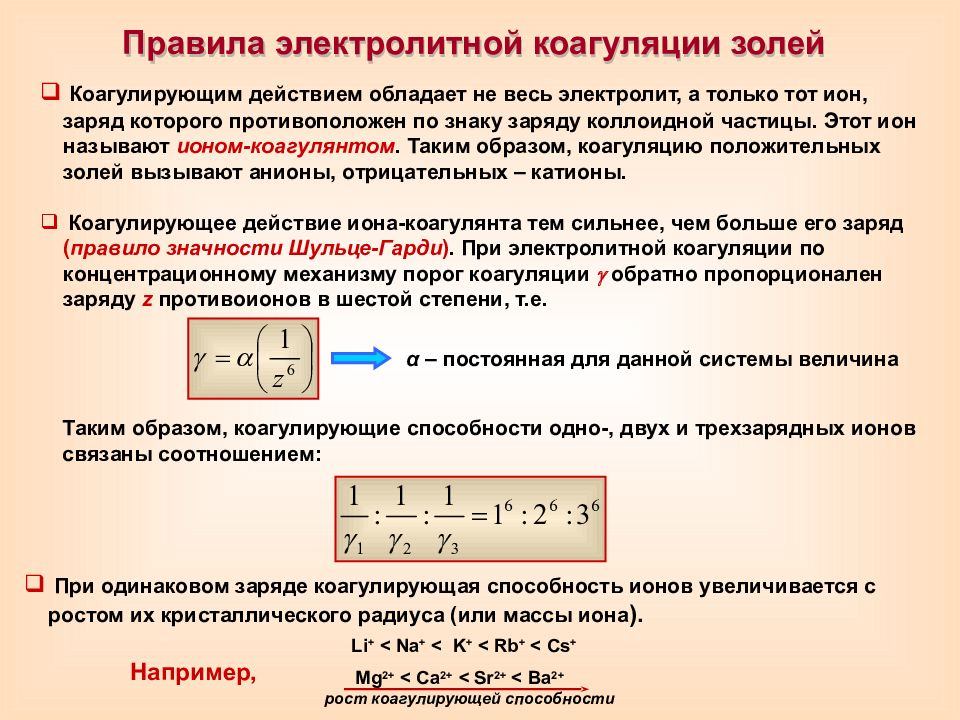
Коагулирующим действием обладает не весь электролит, а только тот ион, заряд которого противоположен по знаку заряду коллоидной частицы. Этот ион называют ионом-коагулянтом. Таким образом, коагуляцию положительных золей вызывают анионы, отрицательных – катионы. Коагулирующее действие иона-коагулянта тем сильнее, чем больше его заряд ( правило значности Шульце-Гарди ). При электролитной коагуляции по концентрационному механизму порог коагуляции обратно пропорционален заряду z противоионов в шестой степени, т.е. Таким образом, коагулирующие способности одно-, двух и трехзарядных ионов связаны соотношением: Li + < Na + < K + < Rb + < Cs + Mg 2+ < Ca 2+ < Sr 2+ < Ba 2+ рост коагулирующей способности Правила электролитной коагуляции золей α – постоянная для данной системы величина Например, При одинаковом заряде коагулирующая способность ионов увеличивается с ростом их кристаллического радиуса (или массы иона ).
Слайд 79
Определение порога коагуляции Порог коагуляции золя по конкретному электролиту устанавливается экспериментально добавлением к фиксированному объему золя V з небольших объемов раствора электролита известной концентрации c эл. до появления первых признаков коагуляции (помутнение, возможно изменение окраски). В этом случае порог коагуляции рассчитывают с учетом разбавления золя раствором электролита: V эл. – объем электролита, израсходованный на коагуляцию золя Если известен порог коагуляции золя по одному электролиту 1 с зарядом иона-коагулянта z 1, пользуясь правилом значности, можно рассчитать порог коагуляции этого же золя по другому электролиту 2 с зарядом иона-коагулянта z 2 :
Слайд 81
ОПТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ При падении луча света на дисперсную систему могут наблюдаться прохождение света через систему, преломление, отражение, рассеивание и поглощение света частицами дисперсной фазы. Преобладающий характер наблюдаемых явлений зависит от размеров частиц дисперсной фазы и их соотношения с длиной волны падающего света Видимый спектр Длина волны ( ), нм 600 500 400 700 Ограничимся рассмотрением видимой области спектра, длина световой волны которого колеблется от 400 нм (фиолетовый свет) до 700 – 750 нм (красный свет). Прохождение света характерно для прозрачных систем (истинных растворов, чистых жидкостей). Размер частиц в них (молекул, ионов) намного меньше длины волны падающе-го света, поэтому частицы не создают препятствий для прохождения лучей видимого света. Преломление и отражение света характерно для средне- и грубодисперсных систем (суспензий, эмульсий), содержащих частицы дисперсной фазы, размер которых намного превышает длину волны падающего света. Попадая на поверхность частиц, световые лучи отражаются под различными углами и выходят из системы в разных направлениях. Прямому прохождению лучей через дисперсную систему препятствуют также многократные отражения и преломления при переходах частица – дисперсионная среда и наоборот. Это обусловливает мутность таких систем, видимую невооруженным глазом. Рассеяние света во всех направлениях наблюдается для систем, в которых размер частиц дисперсной фазы меньше, но соизмерим с длиной волны падающего света. Именно такое соотношение выполняется для коллоидных систем с размером частиц от 1 до 100 нм. Поглощение света ( абсорбция ) характерно для окрашенных коллоидных растворов
Слайд 82
Рассеяние света коллоидными частицами. Эффект Тиндаля Джон Тиндаль (1820-1893) Явление рассеяния света коллоидными системами впервые изучено М. Фарадеем в 1857 г. на примере золей золота. Более подробно это явление было описано Дж. Тиндалем в 1869 г. Тиндаль обнаружил, что если направить на золь пучок света, то при наблюдении освещаемого сосуда сбоку внутри золя можно увидеть светящийся голубым светом конус (эффект Тиндаля ). Это свечение было названо опалесценцией. Схема эффекта Тиндаля Подобное явление можно наблюдать при прохождении луча света через темное запыленное помещение, при свете автомобильных фар и фонарей в туманную погоду. В истинных растворах и чистых жидкостях эффект Тиндаля не наблюдается. Поэтому им часто пользуются для того, чтобы отличить коллоидный раствор от истинного (например, золь берлинской лазури от раствора медного купороса), по внешнему виду это не всегда возможно сделать.
Слайд 83
Уравнение Релея Теорию светорассеяния создал английский ученый Релей. Он вывел уравнение, связывающее интенсивность рассеянного света I р с интенсивностью падающего света I 0 : где n д / ф, n д /с – показатели преломления дисперсной фазы и дисперсионной среды; – численная концентрация частиц; V – объем частицы; λ – длина волны падающего света Уравнение Релея применимо для коллоидных систем, в которых частицы дисперсной фазы имеют сферическую форму, не поглощают свет и не проводят электрический ток, а расстояние между частицами больше длины волны падающего света. Джон Уильям Стрэт (лорд Рэлей) (1842-1919) Интенсивность рассеянного света тем больше, чем сильнее различаются показа- тели преломления дисперсной фазы и дисперсионной среды. Если n д / ф n д /с, то светорассеяние отсутствует и в неоднородной среде Анализ уравнения: Интенсивность рассеянного света обратно пропорциональна λ 4. Следовательно, если источник падающего света содержит волны различной длины (белый свет), то наиболее сильно будут рассеиваться самые короткие волны (синей и фиоле- товой частей спектра). Поэтому бесцветный золь в рассеянном свете имеет голу- боватую окраску, а в проходящем – красноватую.
Слайд 84
Голубой цвет неба обусловлен рассеянием света мельчайшими частицами пыли и капельками воды в атмосфере. Зависимость интенсивности рассеянного света от λ имеет практическое значение. Красный цвет выбран сигналом опасности, так как он виден даже в туманную погоду на больших расстояниях вследствие малого рассеяния. Лампы синего цвета применяются для светомаскировки: при прохождении через толстый слой атмосферы синие лучи почти полностью рассеиваются. Оранжевый или красный цвет неба при восходе или заходе солнца объясняется тем, что при расположении солнца вблизи горизонта наблюдается, главным образом, свет, прошедший через атмосферу.