Команда «Вороново» ГУО «Вороновская средняя школа» Задача №1 ИГРЫ НА ШКОЛЬНОЙ ДОСКЕ
Два мальчика играют в такую игру: по очереди ставят ненулевые цифры в клетки таблицы 1 x 6 (в каждую клетку ровно одну цифру). Первый старается сделать так, чтобы получившееся шестизначное число не делилось на 9, а второй – чтобы делилось. Кто из них выиграет при правильной игре? (Каждый старается выиграть.) а) Рассмотрите игру, в которой игроки могут выбирать любую свободную клетку для своего хода. б) Рассмотрите игру, в которой игроки записывают цифры слева направо по порядку.
1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a b c например 6 3 7 2 5 4 9 9 4 5 8 1 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a b c например 6 3 7 2 5 4 9 9 4 5 8 1
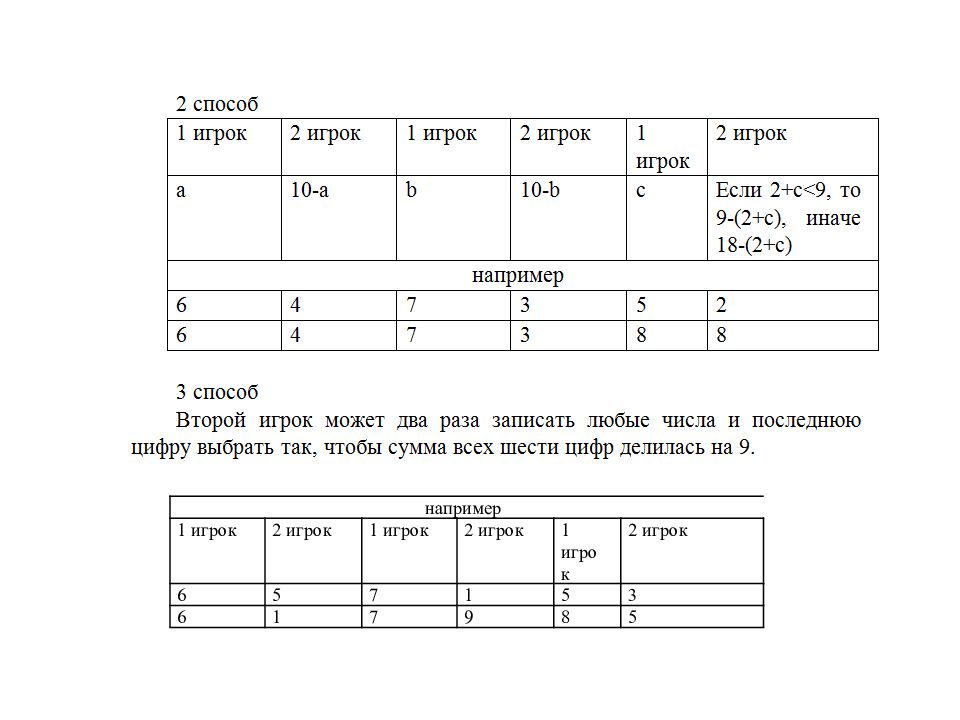
например 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 6 5 7 1 5 3 6 1 7 9 8 5
2. Ответьте на те же вопросы, если число должно делиться на 11 (первый хочет, чтобы не делилось, а второй – чтобы делилось). 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a a b b c c 6 6 7 7 5 5 Решение: Число делится на 11, если сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. Сначала рассмотрим пункт б), игроки записывают цифры слева направо по порядку. Поскольку количество клеток четное – 6, то второй игрок может повторять действия первого, то есть написать те же цифры. В итоге сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах. Значит, число будет делиться на 11 и выиграет второй игрок.
1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок a b c например 1 6 3 7 2 5 4 3 9 9 4 5 8 1 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок a b c например 1 6 3 7 2 5 4 3 9 9 4 5 8 1
а) Рассмотрите игру, в которой игроки могут выбирать любую свободную клетку для своего хода. Решение: Поскольку признак делимости на 9 не зависит от порядка цифр, то разницы между пунктами а) и б) нету. Главное что количество клеток 7, следовательно, первый и последний шаг у первого игрока. При правильной игре выиграет первый игрок. Он может применять тактику с пункта б) заполняя каждый раз любую свободную клетку. Ответ: в обоих пунктах при правильной игре выиграет первый игрок.
1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a b c d 6 3 9 9 5 4 2 7 9 9 4 5 8 1 3 6 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a b c d 6 3 9 9 5 4 2 7 9 9 4 5 8 1 3 6 1 способ:
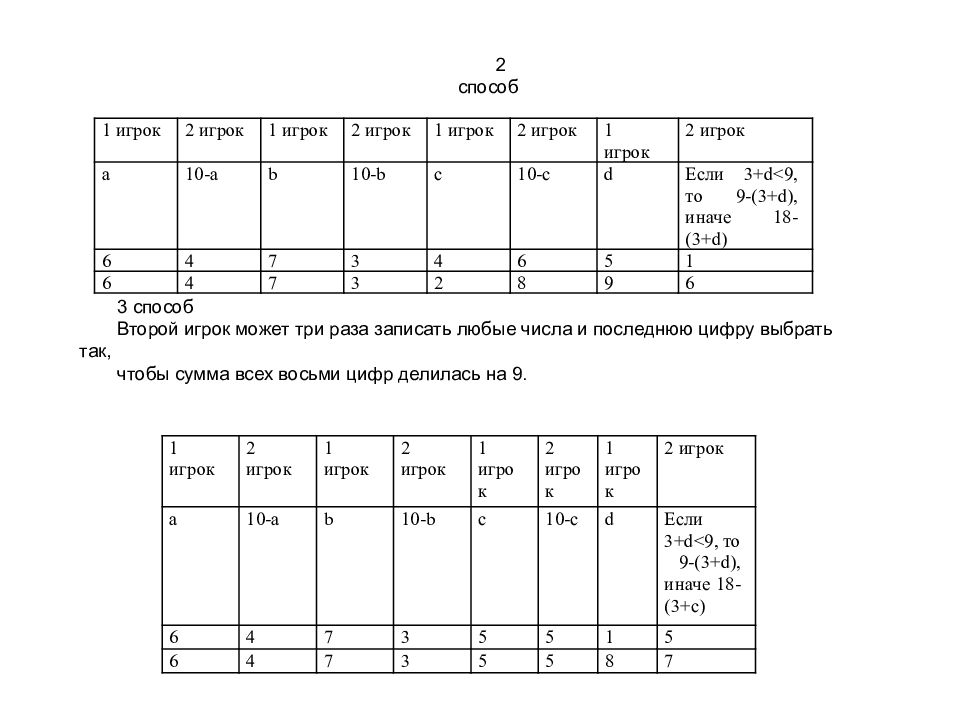
1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a 10-a b 10-b c 10-c d Если 3+ d <9, то 9-(3+ d ), иначе 18-(3+ d ) 6 4 7 3 4 6 5 1 6 4 7 3 2 8 9 6 2 способ 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок a 10-a b 10-b c 10-с d Если 3+ d <9, то 9-(3+ d ), иначе 18-(3+ c ) 6 4 7 3 5 5 1 5 6 4 7 3 5 5 8 7 3 способ Второй игрок может три раза записать любые числа и последнюю цифру выбрать так, чтобы сумма всех восьми цифр делилась на 9.
а) Рассмотрите игру, в которой игроки могут выбирать любую свободную клетку для своего хода. Поскольку признак делимости на 9 (сумма цифр числа делиться на 9) не зависит от порядка цифр, то разницы между пунктами а) и б) нету. Второй игрок может заполнить любую свободную клетку. Главное что количество клеток 8, следовательно, последний шаг у второго игрока и при правильной игре он выиграет. Ответ: а) выиграет второй игрок; б) выиграет второй игрок.
5) Кто выиграет в условиях пункта 1 и 2, если каждую цифру можно использовать более 1 раза? Замечание: В условиях пункта 1 и 2 нет требование, что каждую цифру можно использовать не более одного раза! Рассмотрим пункты 1 и 2, если каждую цифру можно использовать не более 1 раза.
Решение: Сначала рассмотрим пункт б) игроки записывают цифры слева направо по порядку. При правильной игре выиграет 1 игрок. Он сначала скажет 9. Потом каждый раз выберет число так, чтобы вместе с последним числом второго игрока в сумме было 9. После пяти ходов сумма цифр будет кратно девяти. Для последней клетки второй игрок не может выбрать 9, при выборе любого другого числа сумма всех шести цифр не будет кратно 9, значит получившееся шестизначное число не будет делится на 9. 1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 9 a 9-a b 9-b c например 9 3 6 2 7 4 9 1 8 5 4 6
2.Ответьте на те же вопросы, если число должно делиться на 11 (первый хочет, чтобы не делилось, а второй – чтобы делилось). Два мальчика играют в такую игру: по очереди ставят ненулевые цифры в клетки таблицы 1х 6 (в каждую клетку ровно одну цифру и каждую цифру можно использовать не более 1 раза ). Первый старается сделать так, чтобы получившееся шестизначное число не делилось на 11, а второй – чтобы делилось. Кто из них выиграет при правильной игре? (Каждый старается выиграть.) Решение: Число делится на 11, если сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. Сначала рассмотрим пункт б), игроки записывают цифры слева направо по порядку. Первый игрок может последним своим ходом создать одну из следующих ситуации: Сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах Сумма цифр, которые стоят на четных местах, отличается на 11 от суммы цифр, стоящих на нечетных местах Поскольку второй игрок должен вставить ненулевую цифру, то итоговое число не будет делиться на 11.
1 игрок 2 игрок 1 игрок 2 игрок 1 игрок 2 игрок 5 9 6 8 4 – 6 8 7 9 4 – 6 4 7 3 5 – Например: а) Рассмотрим игру, в которой игроки могут выбирать любую свободную клетку для своего хода. Игроки могут рассмотреть клетки парами первый со вторым, третий с четвертым и пятый с шестым. Второй игрок может помешать первому, то есть занять клетки первого. Например, если первый напишет в третей клетке, то второй может занять первое или пятое. В итоге не у кого не будет выигрышной ситуации. Ответ: а) При правильной игре выиграет 1 игрок; б) нет выигрышной ситуации. Контрпример ??? Замечание: первому игроку следует начинать из средних чисел, иначе если он скажет относительно большие (маленькие) цифры, то второй может сказать маленькие (большие) числа и разность цифр на четных и нечетных местах может быть больше девяти. Тогда первому не получится приравнивать суммы на четных и нечетных местах. А чтобы суммы отличались на 11, необходимая цифра может быть уже использовано.
Предложите свои обобщения или направления исследований в этой задаче и изучите их. Замечание: во всех следующих пунктах будем считать, что цифры могут повторяться.
