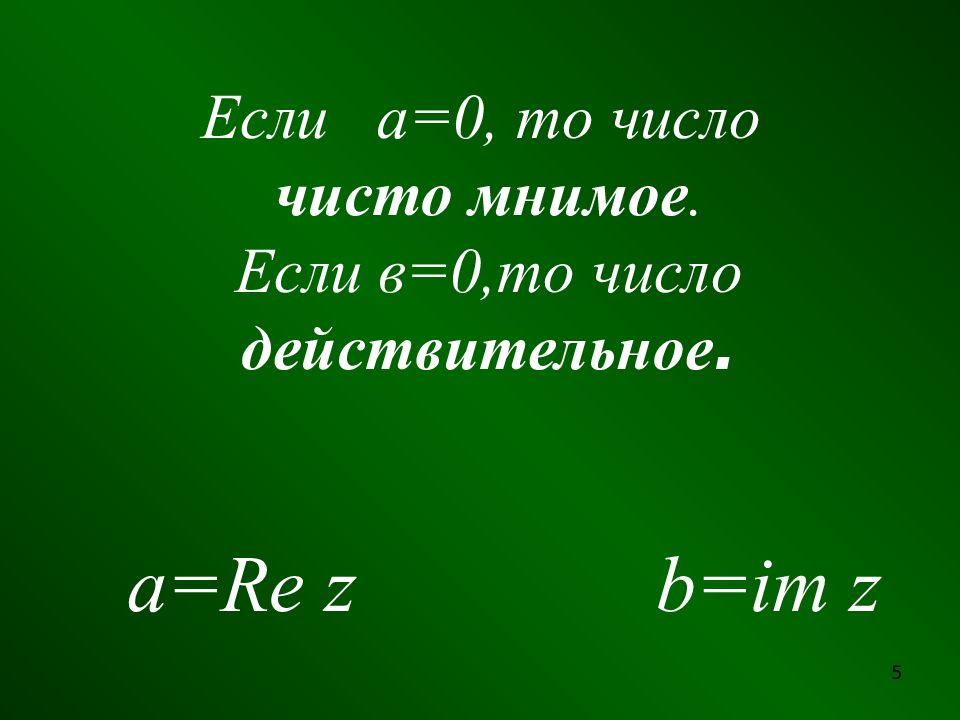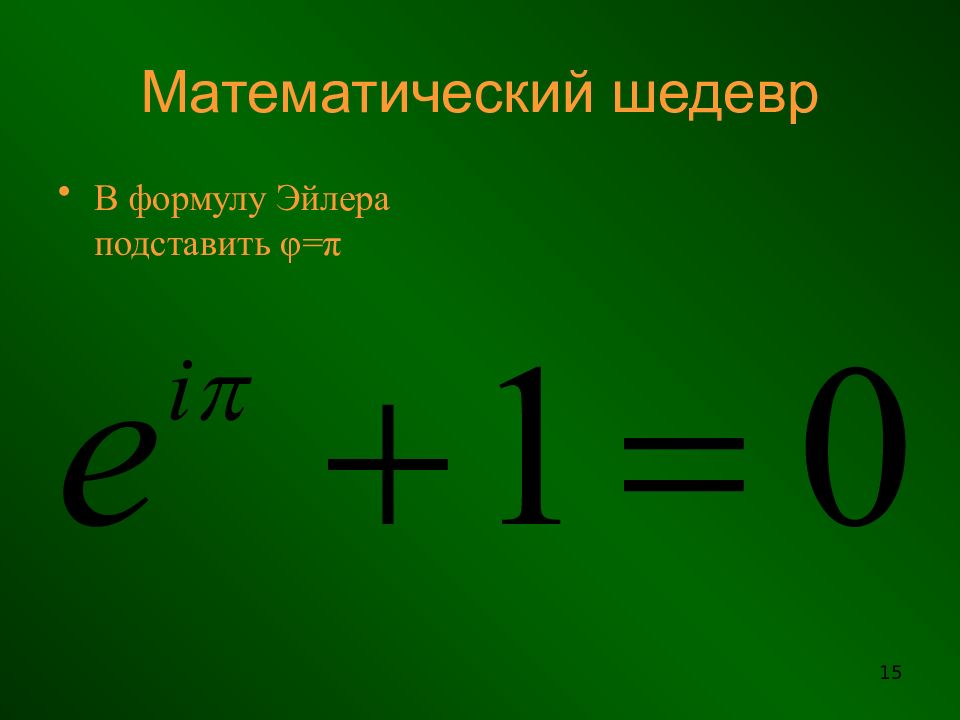Первый слайд презентации: Комплексные числа. Основные понятия. Формы записи
Преподаватель: Божкова О.В. 1
Слайд 2: Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием» Г. Лейбниц
2
Слайд 3: Как все начиналось… (из истории комплексных чисел)
16 век. Италия. Математический турнир между Фиоре и Никколо Тарталья. Надо решить 30 уравнений третьей степени. Решение некоторых знал Фиоре от своего учителя – профессора Болонского университета дель Ферро. Победил Тарталья, предложив общий вид решения этих уравнений. (Надо допустить существование некоторого числа квадрат которого равен -1) 17 век. Рене Декарт ввел название «мнимые числа» 18 век Леонард Эйлер ввел обозначение мнимой единицы, предложив использовать первую букву французского слова imaginare ( мнимый). 19 век. Карл Гаусс ввел название комплексные числа, дал им геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный или мнимый корень 3
Слайд 4: Определение комплексного числа
а и в – действительные числа, i- мнимая единица, квадрат которой равен -1 4
Слайд 5: Если а=0, то число чисто мнимое. Если в=0,то число действительное
а= Re z b=im z 5
Слайд 7: Действия над комплексными числами z 1 = a 1 +b 1 i и z 2 = a 2 +b 2 i
Сложение: z 1 +z 2 = (a 1 + a 2 )+(b 1 +b 2 )i Вычитание: z 1 - z 2 = (a 1 - a 2 )+(b 1 - b 2 )i Умножение: z 1 * z 2 =(a 1 a 2 - b 1 b 2 )+(a 1 b 2 + a 2 b 1 )i Умножение комплексно – сопряженных чисел: z * ž= Деление: 7
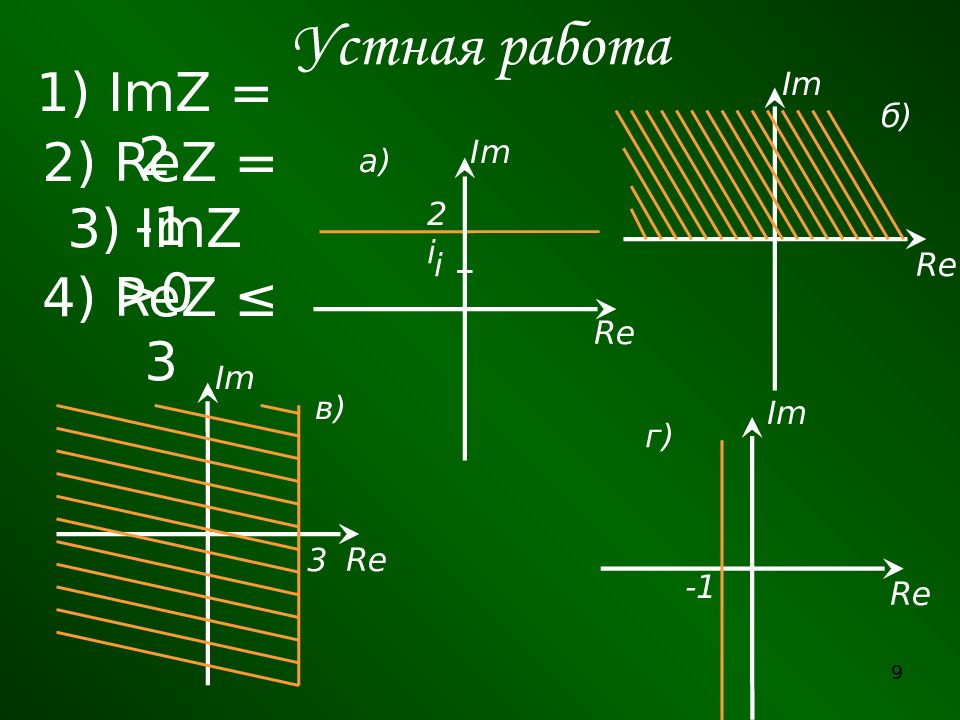
Слайд 9: Устная работа
1) ImZ = 2 2) ReZ = -1 3) ImZ >0 4) ReZ ≤ 3 Im Re i 2 i Im Re а) б) 3 Im Re в) -1 Re Im г) 9
Слайд 10: Формы записи комплексных чисел
Алгебраическая z=a+bi Тригонометрическая ( а =rcos φ, b=rsin φ ) z= r(cos φ +isin φ ) Показательная 10
Слайд 11: Показательная форма записи комплексного числа
Формула Эйлера = cos φ +isin φ Показательная форма z=r 11
Слайд 12: Переход от одной формы к другой
Задание : 1.Записать комплексное число z=-1+i в тригонометрической и показательной формах. 2.Ответ проверить обратным переходом 12
Слайд 13: Действия над комплексными числами в тригонометрической и показательной формах
Тригонометрическая Показательная 1.Умножение 2.Деление 3. Возведение в степень 13