Лекция 22 5. Оптика 5.1. Геометрическая оптика Законы геометрической оптики. Отражение и преломление света. Угол Брюстера. Ход лучей в плоко-параллельной пластинке, призме. Построение изображений в зеркалах, линзах. Формула тонкой линзы. Оптические приборы: лупа, фотоаппарат, проекционный аппарат, микроскоп, телескоп. Глаз. Корпускулярная и волновая теории света. Принцип Гюйгенса. Вывод закона преломления. Связь показателя преломления со скоростью света в среде.
Оптика Оптика (от др.-греч. ὀπτική – взгляд ) – учение о свете – изучает физические явления, связанные с излучением и распространением света, а также его взаимодействием с веществом. Геометрическая оптика Раздел оптики, изучающий распространение световой энергии в прозрачных средах на основе представления о световых лучах. Световой луч Световой луч – воображаемая геометрическая линия, 1) вдоль которой распространяется свет (световая энергия); 2) проведенная перпендикулярно к волновому фронту (т.е. поверхности одинаковой фазы колебаний) и указывающая направление распространения волнового возмущения. Чтобы определить это направление, выделяют узкие световые пучки (диаметр которых значительно превышает длину волны). Линии, являющиеся осями этих пучков, и есть световые лучи.
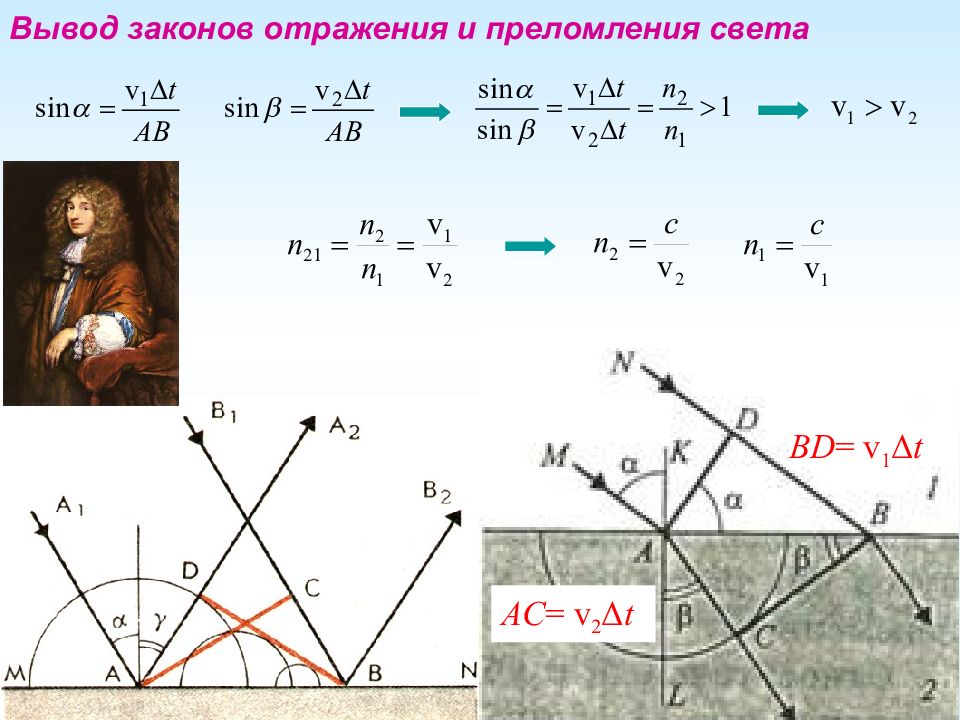
Законы геометрической оптики Закон прямолинейного распространения света: свет в однородной изотропной среде распространяется прямолинейно. Доказательство – существование тени. Знают даже животные. Закон обратимости световых пучков: при распространении в обратном направлении свет проходит тот же путь и возвращается к источнику. Закон независимости световых пучков: распространение всякого светового пучка в среде не зависит от того, есть ли в ней другие пучки. Закон отражения на плоской границе двух сред: а) отраженный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной из точки падения; б) угол падения равен углу отражения. Закон преломления на плоской границе двух прозрачных сред: а) преломленный луч лежит в одной плоскости с падающим лучом и нормалью, восстановленной из точки падения; б) отношение синуса угла падения к синусу угла преломления не зависит от угла падения и есть величина постоянная для данных двух сред.
– относительный показатель преломления второй среды ( 2 ) по отношению к первой ( 1 ); – наоборот, 1 по отношению ко 2. Показатель преломления какой-либо среды относительно вакуума называется абсолютным показателем преломления этой среды. Тем самым показатель преломления вакуума принят за единицу. Показатель преломления воздуха. Вода – 1,33 Масло оливковое – 1,46 Стекло – 1,47—2,04 Берилл (изумруд) – 1,581 Турмалин – 1,669 Корунд (рубин, сапфир) – 1,769 Алмаз – 2,42 Среда, у которой показатель преломления больше, называется оптически более плотной, у которой меньше – оптически менее плотной. Можно показать, что Из воздуха в среду с показателем n : Из среды с показателем n в воздух:
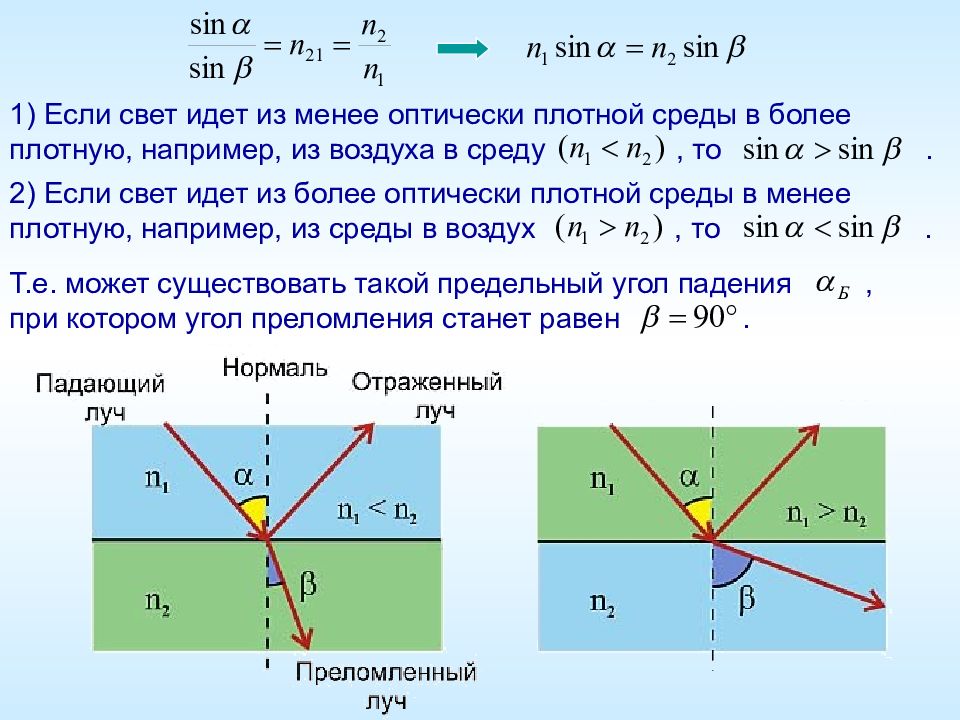
1) Если свет идет из менее оптически плотной среды в более плотную, например, из воздуха в среду, то. 2) Если свет идет из более оптически плотной среды в менее плотную, например, из среды в воздух, то. Т.е. может существовать такой предельный угол падения, при котором угол преломления станет равен.
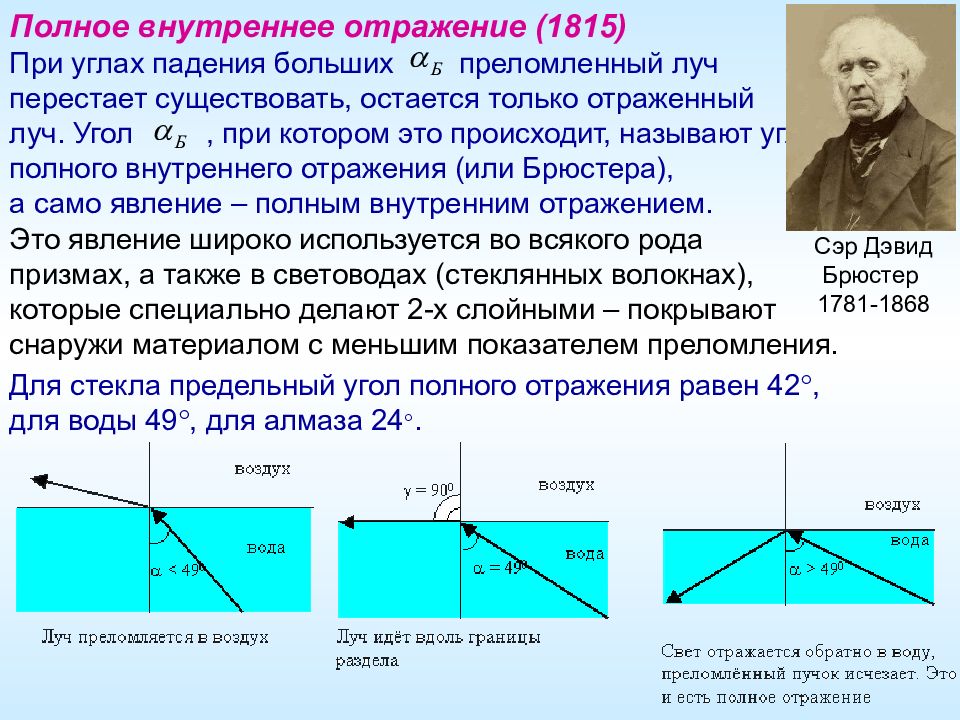
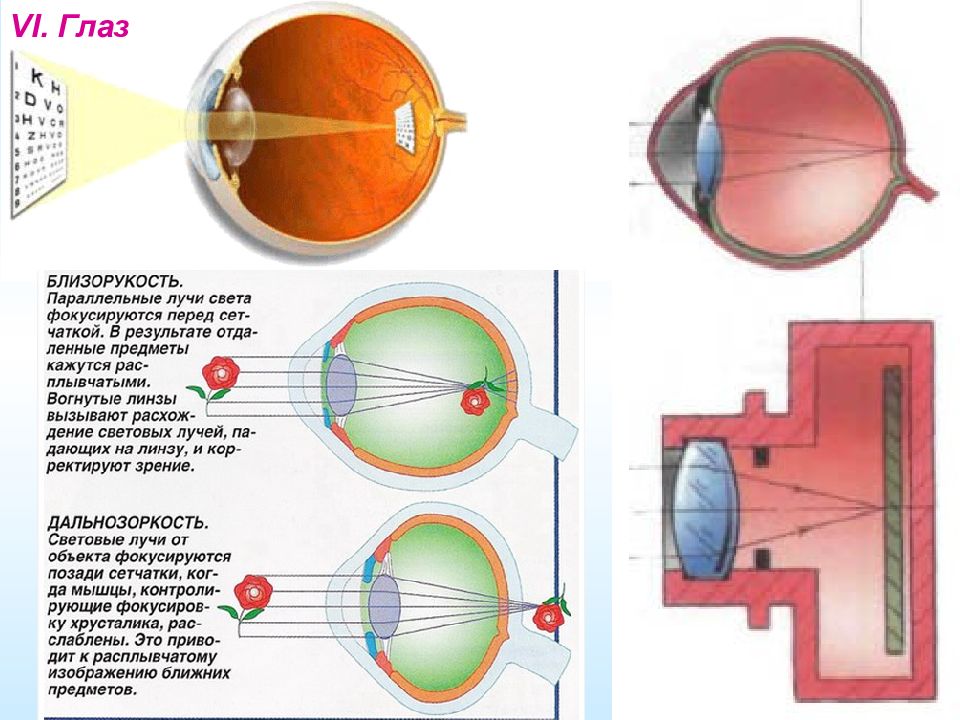
Полное внутреннее отражение (1815) При углах падения больших преломленный луч перестает существовать, остается только отраженный луч. Угол, при котором это происходит, называют углом полного внутреннего отражения (или Брюстера), а само явление – полным внутренним отражением. Это явление широко используется во всякого рода призмах, а также в световодах (стеклянных волокнах), которые специально делают 2-х слойными – покрывают снаружи материалом с меньшим показателем преломления. Сэр Дэвид Брюстер 1781-1868 Для стекла предельный угол полного отражения равен 42 , для воды 49 , для алмаза 24 .
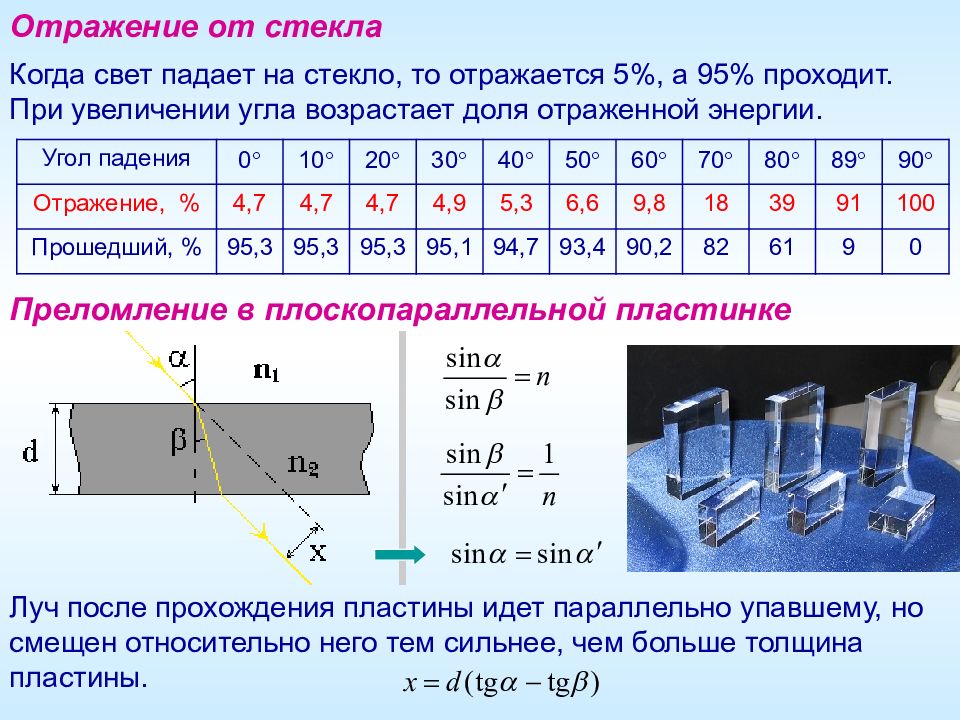
Когда свет падает на стекло, то отражается 5%, а 95% проходит. При увеличении угла возрастает доля отраженной энергии. Угол падения 0 10 20 30 40 50 60 70 80 89 90 Отражение, % 4,7 4,7 4,7 4,9 5,3 6,6 9,8 18 39 91 100 Прошедший, % 95,3 95,3 95,3 95,1 94,7 93,4 90,2 82 61 9 0 Отражение от стекла Преломление в плоскопараллельной пластинке Луч после прохождения пластины идет параллельно упавшему, но смещен относительно него тем сильнее, чем больше толщина пластины.
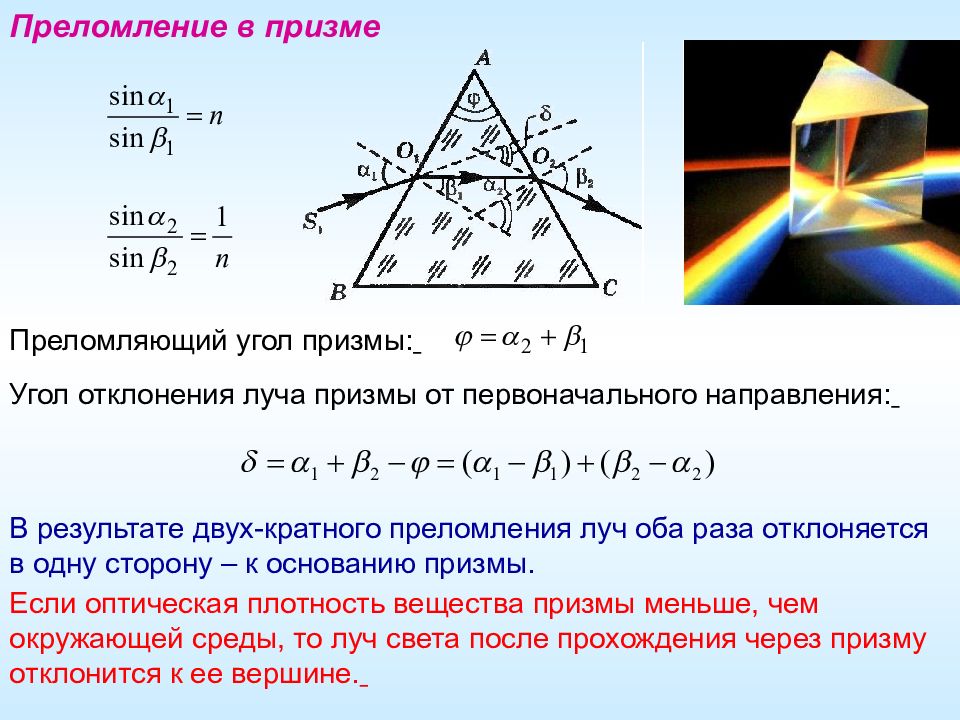
В результате двух-кратного преломления луч оба раза отклоняется в одну сторону – к основанию призмы. Если оптическая плотность вещества призмы меньше, чем окружающей среды, то луч света после прохождения через призму отклонится к ее вершине. Преломление в призме Преломляющий угол призмы: Угол отклонения луча призмы от первоначального направления:
Построение изображений Для построения изображения точки достаточно построить любые два луча, идущие от данной точки предмета. Лучи, входящие в оптическую систему – падающие, после преобразования – выходящие. Точка пересечения выходящих лучей, соответствующим этим двум падающим, будет искомым изображением точки. Выходящие лучи могут быть сходящимися или расходящимися. В первом случае они действительно пересекутся, и полученное изображение будет действительным. Во втором случае пересекутся "продолжения" лучей и изображение будет мнимым. На вид отличить их невозможно, но в первой точке действительно выделяется световая энергия, а во второй точке энергия туда не попадает (например, фотопластинка не засветится). Зеркальная поверхность
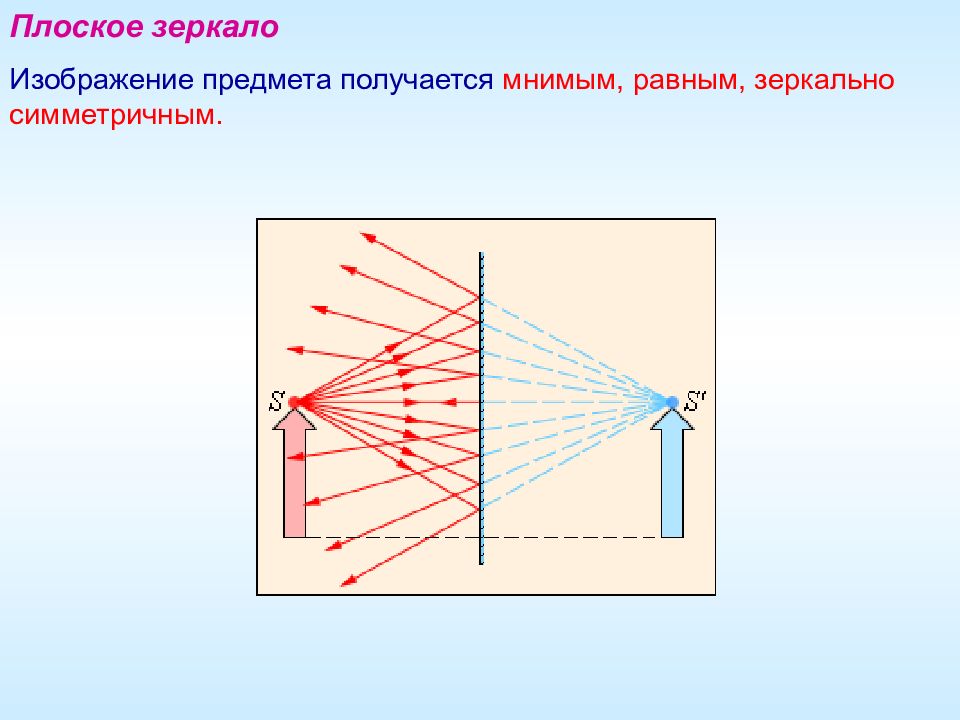
Плоское зеркало Изображение предмета получается мнимым, равным, зеркально симметричным.
Линза (нем. Linse, от лат. lens – чечевица) Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Прямая, проходящая через центры этих сфер – главная оптическая ось. Линзы, отклоняющие лучи в сторону главной оптической оси – собирающие, от главной оси – рассеивающие. Если толщина самой линзы много меньше радиусов кривизны поверхностей, то линза считается тонкой. Точка пересечения тонкой линзы с главной оптической осью – оптический центр линзы. Лучи, проходящие через оптический центр, не преломляются. Лучи, параллельные главной оптической оси собирающей линзы, пересекаются в одной точке – главном фокусе линзы. У линзы их всегда два (передний и задний). У рассеивающей линзы в фокусе собираются продолжения лучей. Плоскость, перпендикулярная главной оптической оси и проходящая через фокус – фокальная плоскость.
Построение изображений в тонкой линзе Луч, параллельный главной оптической оси, пройдет через фокус. Луч, проходящий через фокус, пойдет параллельно главной оптической оси. Луч, идущий через оптический центр, своего направления не изменит. Фокусное расстояние и оптическая сила линзы Фокусным называется расстояние от центра линзы до фокуса. Величина, обратная фокусному расстоянию, называется оптической силой линзы. Измеряется в диоптриях. Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м. Радиусы выпуклых линз берутся со знаком (+), вогнутых (–). У собирающих линз f и D получаются положительные, у рассеивающих – отрицательные.
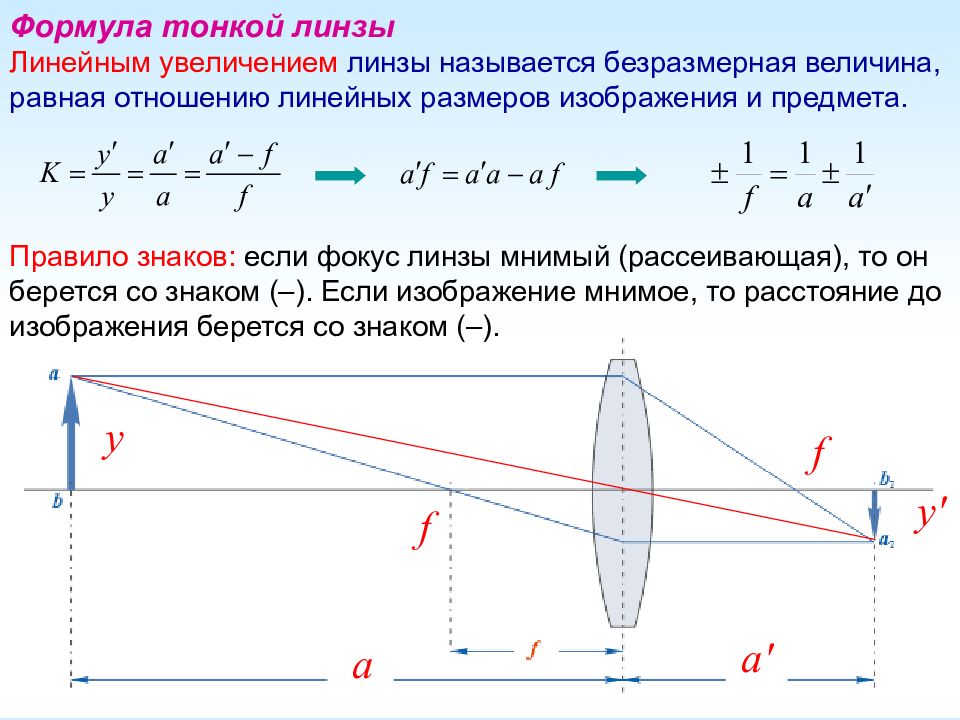
Формула тонкой линзы Линейным увеличением линзы называется безразмерная величина, равная отношению линейных размеров изображения и предмета. Правило знаков: если фокус линзы мнимый (рассеивающая), то он берется со знаком (–). Если изображение мнимое, то расстояние до изображения берется со знаком (–). a a ' f f y y '
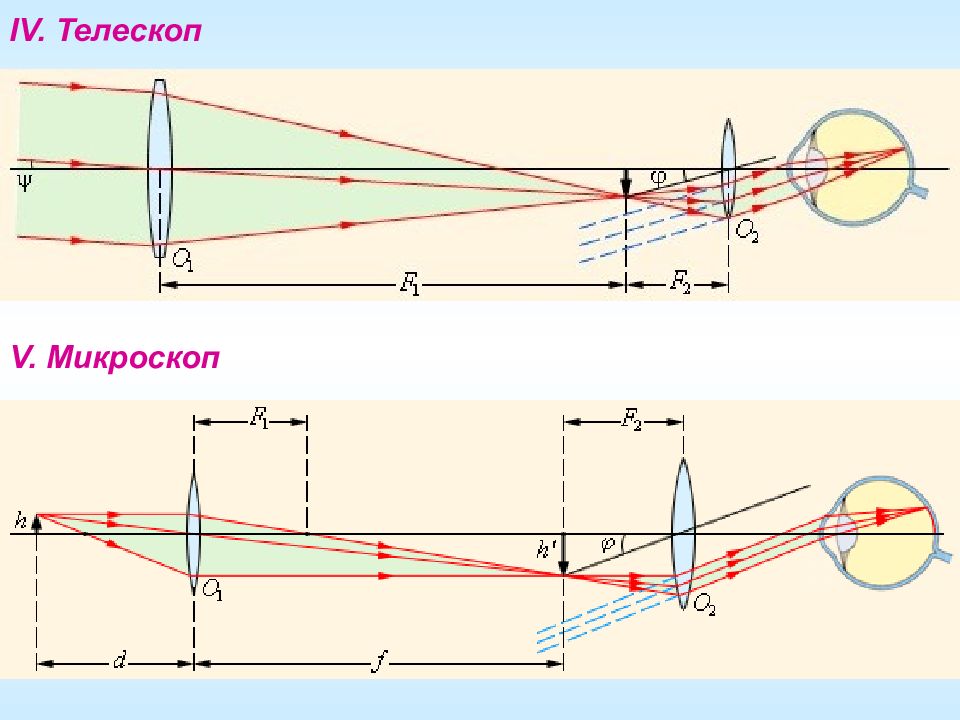
Возможные ситуации положения предмета Предмет бесконечно далеко. Предмет дальше двойного фокусного (I). Предмет на расстоянии равном двойному фокусному. Предмет между двойным фокусным и фокусным расстоянием (II). Предмет на расстоянии равном фокусному. Предмет на расстоянии меньшим фокусного (III). I. Фотоаппарат Если предмет находится дальше, чем двойной фокус, то изображение предмета получается действительным, перевёрнутым, уменьшенным.
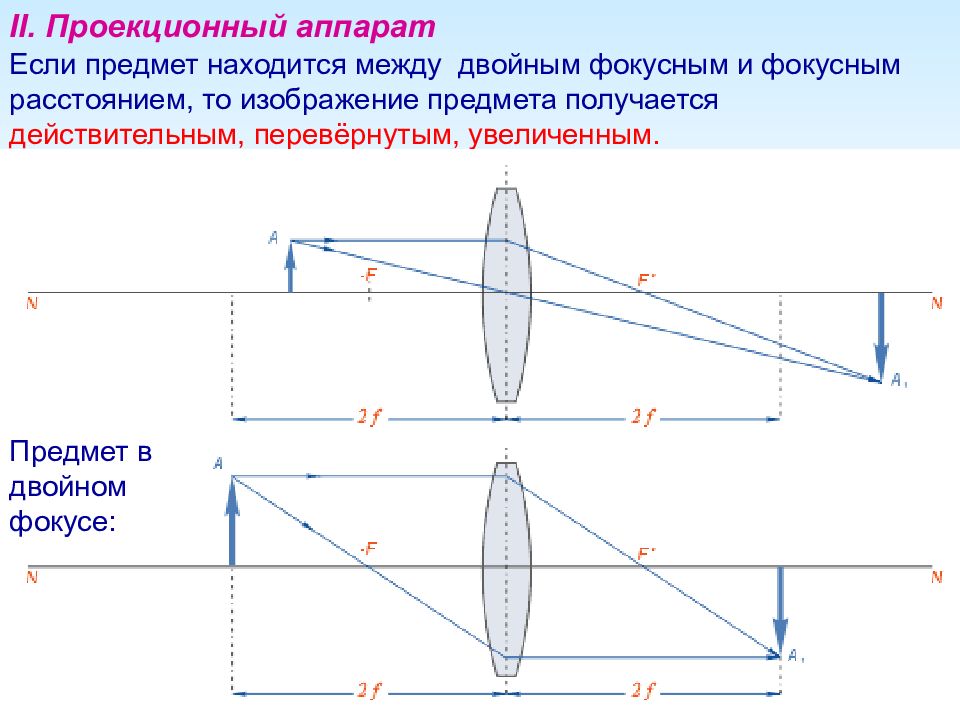
II. Проекционный аппарат Если предмет находится между двойным фокусным и фокусным расстоянием, то изображение предмета получается действительным, перевёрнутым, увеличенным. Предмет в двойном фокусе:
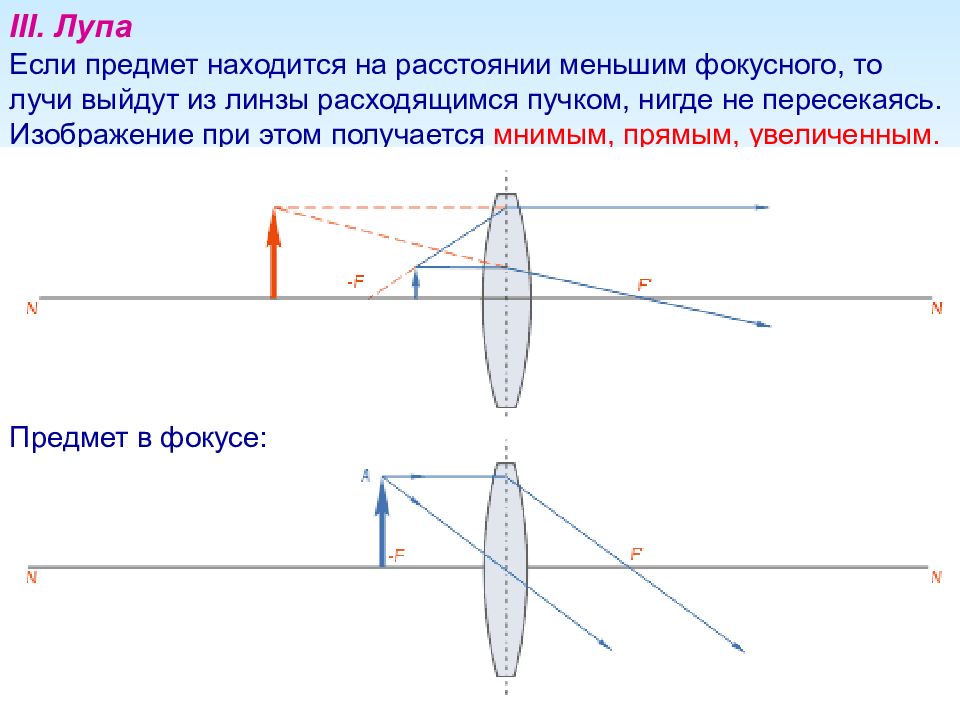
III. Лупа Если предмет находится на расстоянии меньшим фокусного, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимым, прямым, увеличенным. Предмет в фокусе:
IV. Телескоп V. Микроскоп
VI. Глаз
Исаак Ньютон 1 642 -1 7 27 Корпускулярная теория света (Ньютон) Свет состоит из мельчайших частиц (корпускул), испускаемых светящимися телами. Теория позволяла объяснить прямолинейное распространение света, скорость света, независимость световых пучков, закон отражения. Для объяснения преломления пришлось выдвинуть дополнительную гипотезу, что на корпускулу в тонком слое на границе 2 сред действует сила притяжения со стороны оптически более плотной среды. Тогда скорость света в этой среде получалась больше. Различные цвета объяснялись частицами разных размеров. Однако теория не могла объяснить явления интерференции, дифракции, поляризации и пр. Волновая теория света (Гюйгенс) 1) Свет представляет собой продольные волны – колебания, распространяющееся в особой всепроникающей материи, заполняющей собой все пространство – мировом светоносном эфире (по аналогии со звуковыми волнами). Христиан Гюйгенс фон Зейлихен 1629-1695
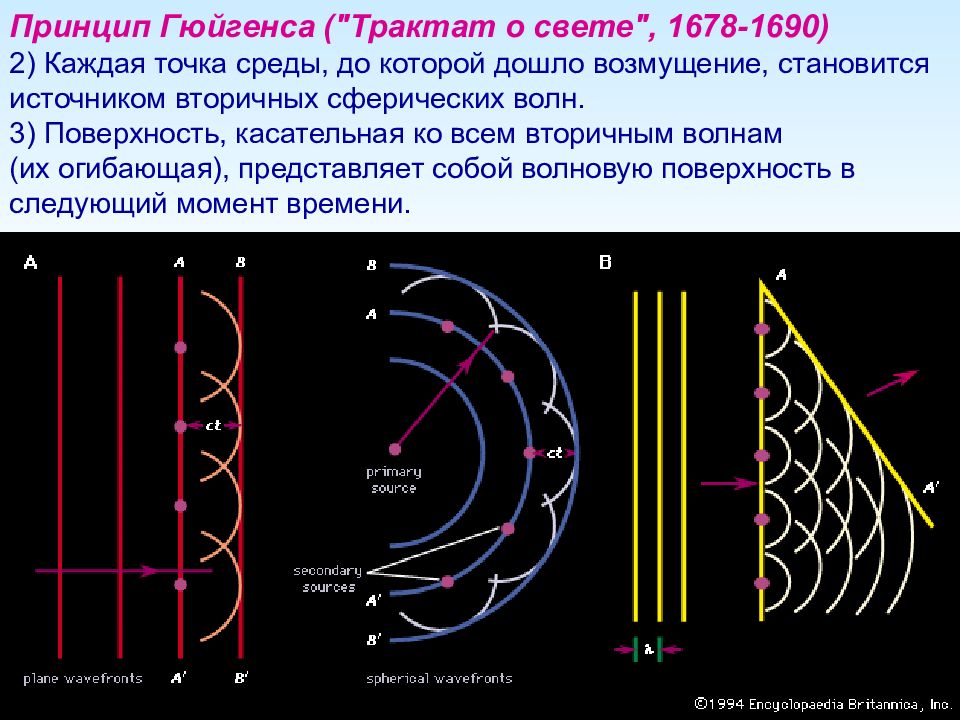
Принцип Гюйгенса ("Трактат о свете", 1678-1690) 2) Каждая точка среды, до которой дошло возмущение, становится источником вторичных сферических волн. 3) Поверхность, касательная ко всем вторичным волнам (их огибающая), представляет собой волновую поверхность в следующий момент времени.
Вывод законов отражения и преломления света BD = v 1 Δ t AC = v 2 Δ t
Относительный показатель преломления равен отношению скоростей света в тех средах, на границе которых происходит преломление. Абсолютный показатель преломления среды показывает, во сколько раз скорость света в среде меньше скорости света в вакууме. Измерение скорости света 1) Галилей – свет распространяется мгновенно. 2) О. Рёмер (1676, Дания) – по запаздыванию затмений спутника Юпитера Ио на 22 минуты c = 215 000 км / сек. 3) Физо (1849, Франция) c = 312 000 км / сек. 4) Фуко (1850, Франция) c = 298 000 км / сек. 5) Майкельсон (1927, США) c = (299 796 ± 4) км / сек. 6) Современные методы (1957) c = (299 792,5 ± 0,4) км / сек. Физический смысл показателя преломления
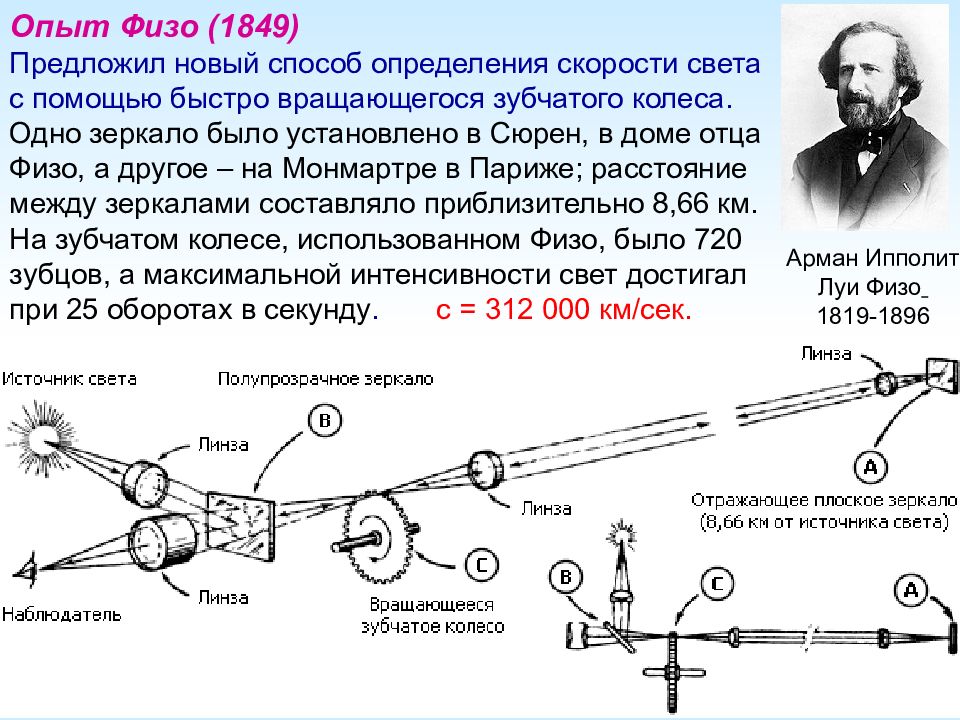
Опыт Физо (1849) Предложил новый способ определения скорости света с помощью быстро вращающегося зубчатого колеса. Одно зеркало было установлено в Сюрен, в доме отца Физо, а другое – на Монмартре в Париже; расстояние между зеркалами составляло приблизительно 8,66 км. На зубчатом колесе, использованном Физо, было 720 зубцов, а максимальной интенсивности свет достигал при 25 оборотах в секунду. c = 312 000 км / сек. Арман Ипполит Луи Физо 1819-1896
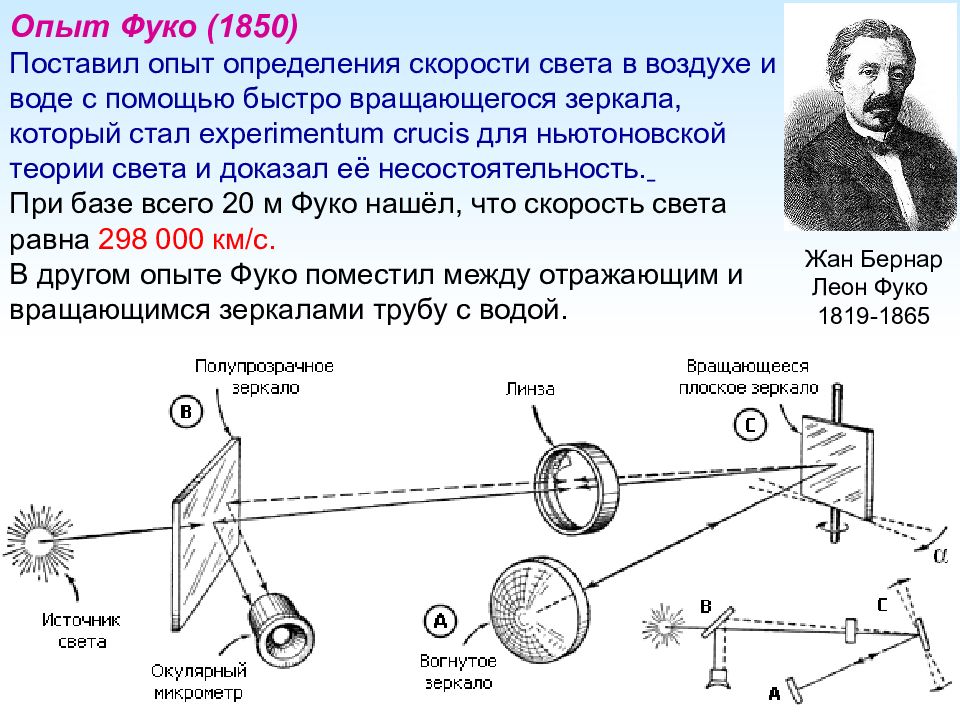
Опыт Фуко (1850) Поставил опыт определения скорости света в воздухе и воде с помощью быстро вращающегося зеркала, который стал experimentum crucis для ньютоновской теории света и доказал её несостоятельность. При базе всего 20 м Фуко нашёл, что скорость света равна 298 000 км/с. В другом опыте Фуко поместил между отражающим и вращающимся зеркалами трубу с водой. Жан Бернар Леон Фуко 1819-1865
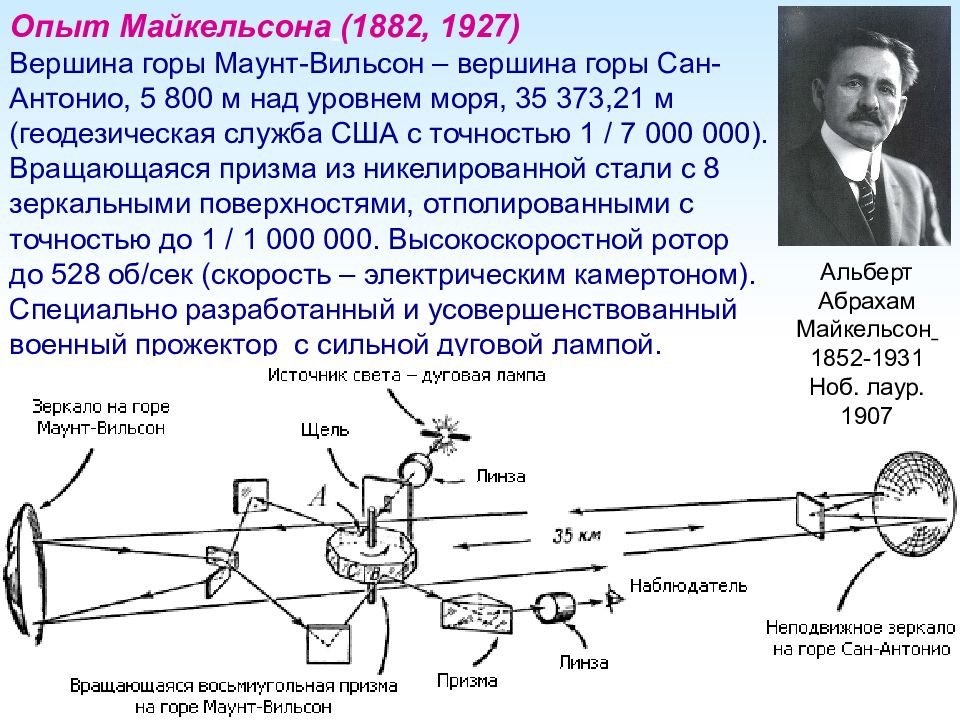
Опыт Майкельсона ( 1882, 1927) Вершина горы Маунт-Вильсон – вершина горы Сан-Антонио, 5 800 м над уровнем моря, 35 373,21 м (геодезическая служба США с точностью 1 / 7 000 000). Вращающаяся призма из никелированной стали с 8 зеркальными поверхностями, отполированными с точностью до 1 / 1 000 000. Высокоскоростной ротор до 528 об/сек (скорость – электрическим камертоном). Специально разработанный и усовершенствованный военный прожектор с сильной дуговой лампой. Альберт Абрахам Майкельсон 1852-1931 Ноб. лаур. 1907
