Первый слайд презентации: Лекция № 6
МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ Лекция № 5-6 МАГНИТНЫЕ ЯВЛЕНИЯ (продолжение) Литература: Иродов И.Е. Электромагнетизм. Основные законы. — М. — С.-П.: Физматлит, 2000.
Слайд 2
Все природные вещества в разной мере обладают магнитными свойствами Магнетики – вещества, способные намагничиваться, если поместить их во внешнее магнитное поле. Магнетики: слабомагнитные ( парамагнетики и диамагнетики ) и сильномагнитные ( ферромагнетики ).
Слайд 3
Атомы и молекулы вещества приобретают магнитный момент Намагничивание – приобретение веществом (его атомами и молекулами) магнитного момента. Пусть индукция магнитного поля в вакууме
Слайд 4
– орбитальный (магнитный) момент электрона, – спиновый магнитный момент, – магнитный момент прецессии, – ядерный момент электрона (им обычно пренебрегаем), z – число электронов в атоме (заряд ядра).
Слайд 5: Магнитный момент контура с током
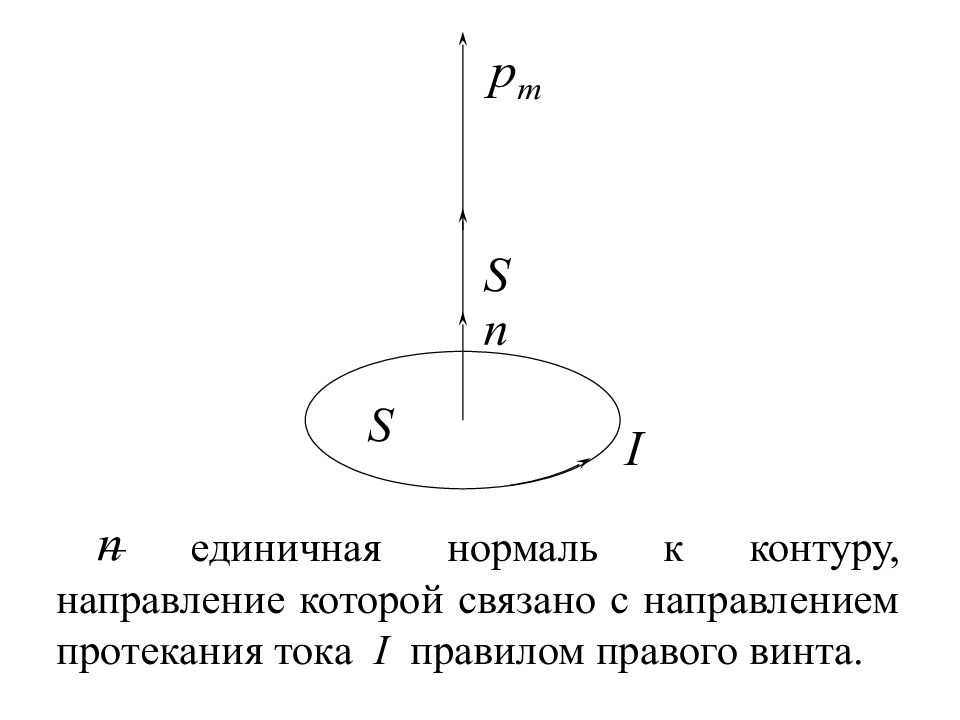
Пробный контур с током – плоский виток с током, очень малой площади. При внесении контура с током в магнитное поле он определенным образом ориентируется. Магнитный момент контура с током
Слайд 6
– единичная нормаль к контуру, направление которой связано с направлением протекания тока I правилом правого винта.
Слайд 7: Намагниченность вещества
Объяснение явления намагничения. Предполагают, что в молекулах вещества циркулируют элементарные круговые токи ( молекулярные токи ), каждый ток обладает магнитным моментом и создает в пространстве магнитное поле. Если поле, обусловленное токами проводимости, отсутствует то моменты отдельных молекул ориентированы беспорядочно
Слайд 8
Под действием внешнего поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вещество намагничивается, т.е. и образуется поле
Слайд 9
Степень намагничения магнетика характеризуют магнитным моментом единицы объема – намагниченностью ( вектором намагничивания ) или (6.1)
Слайд 10
В (6.1): Δ V – физически бесконечно малый объем в окрестности данной точки, магнитный момент отдельной молекулы. Суммирование проводится по всем молекулам в объеме Δ V. Измеряется намагниченность в СИ в А/м. Также можно представить (6.2) – средний магнитный момент одной молекулы, n – концентрация молекул.
Слайд 11
Тогда при наличии магнетика (6.3) где индукция магнитного поля в веществе, индукция магнитного поля, созданного в вакууме токами проводимости, индукция магнитного поля, созданного микротоками внутри магнетика (индукция самого магнетика):
Слайд 12
не имеет источников, нет «магнитных зарядов». Поэтому и для результирующего поля Поле как и поле в магнетике справедлива теорема Гаусса: т.е. силовые линии всегда замкнуты.
Слайд 13
Намагничивание вещества связано с преимущественной ориентацией (а для ряда магнетиков – с индуцированием) молекулярных токов, совокупность которых образует макроскопические токи намагничивания (с плотностью объемного тока и силой тока I ´ ). Токи, текущие по проводникам и связанные с дрейфом в веществе носителей тока – токи проводимости.
Слайд 14
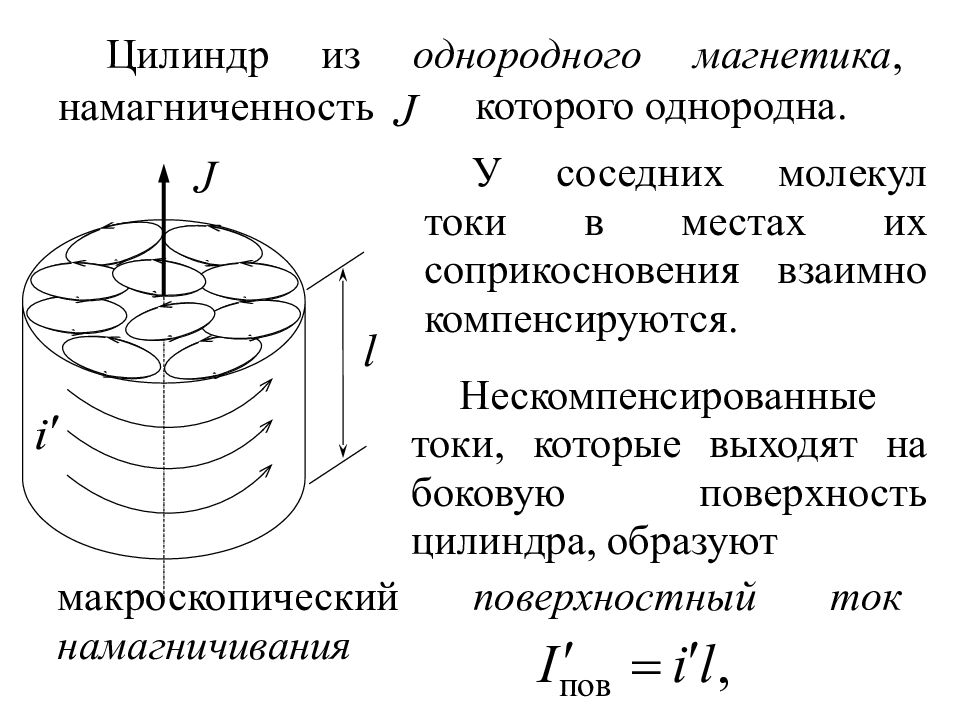
Цилиндр из однородного магнетика, намагниченность У соседних молекул токи в местах их соприкосновения взаимно компенсируются. которого однородна. Нескомпенсированные токи, которые выходят на боковую поверхность цилиндра, образуют макроскопический поверхностный ток намагничивания
Слайд 15
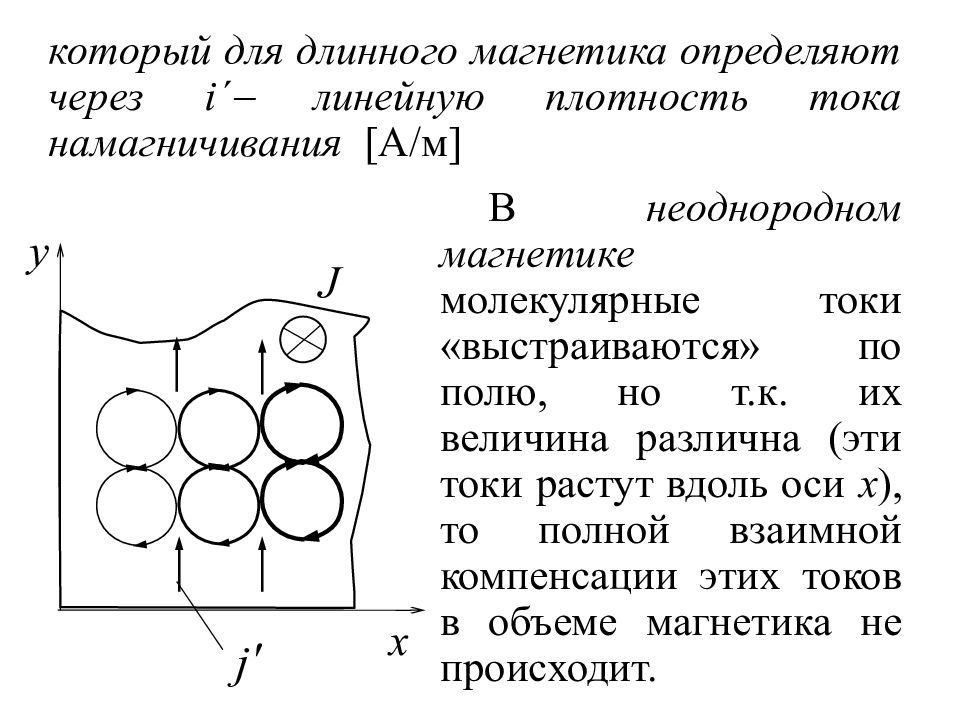
который для длинного магнетика определяют через i ´ линейную плотность тока намагничивания [А/м] В неоднородном магнетике молекулярные токи «выстраиваются» по полю, но т.к. их величина различна (эти токи растут вдоль оси x ), то полной взаимной компенсации этих токов в объеме магнетика не происходит.
Слайд 16
Образуется (наряду с I ´ пов ) макроскопический объемный ток намагничивания I ´ об, текущий вдоль оси y где Δ S сечение магнетика в плоскости xz, поверхностная плотность тока намагничивания [А/м 2 ] равен вкладу, который был бы создан тем же распределением токов I ´ в вакууме. В клад намагниченного магнетика в результирующее поле
Слайд 17
Однако это распределение зависит не только от конфигурации и свойств магнетика, но и от искомого поля Теорема о циркуляции векторов и Докажем интегральную теорему о циркуляции намагниченности : (6.4) циркуляция намагниченности по любому замкнутому контуру L равна алгебраической сумме токов намагничивания I ´, охватываемых данным контуром.
Слайд 18
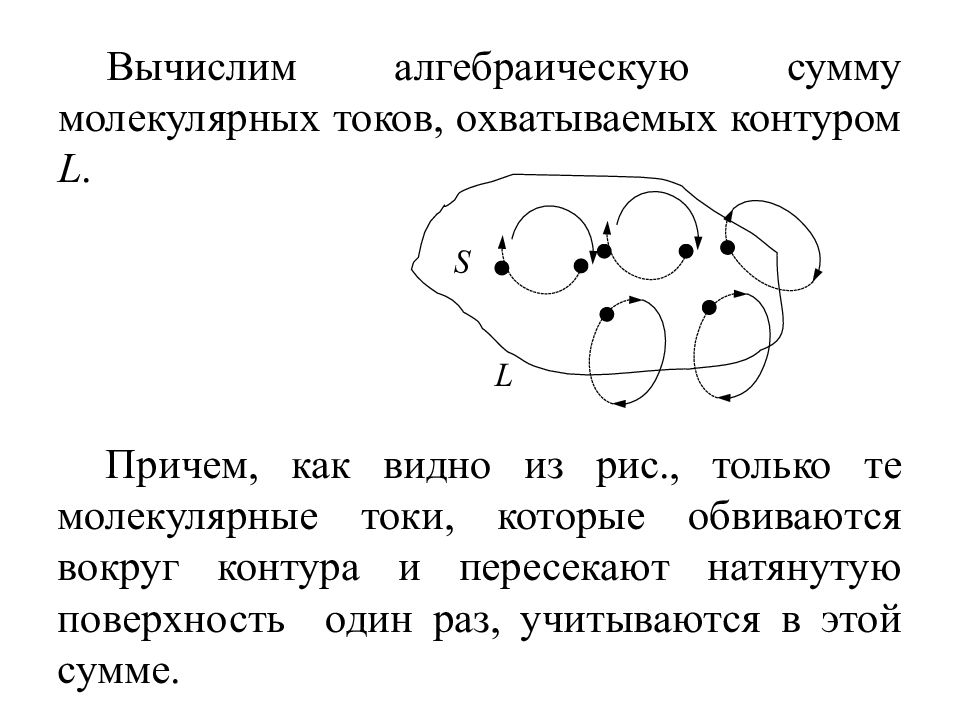
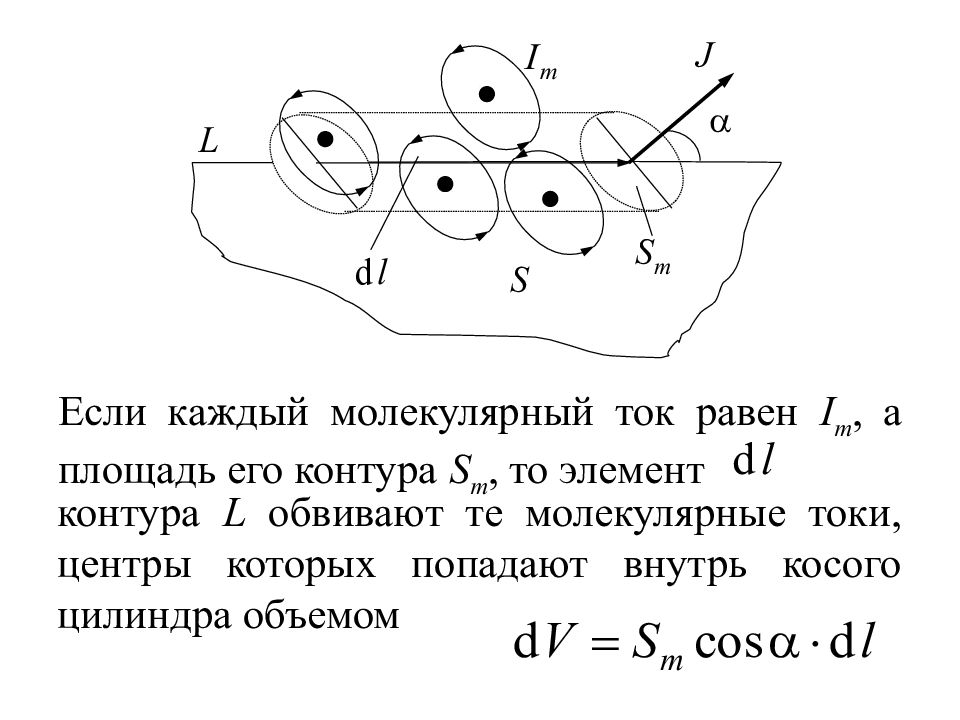
Вычислим алгебраическую сумму молекулярных токов, охватываемых контуром L. Причем, как видно из рис., только те молекулярные токи, которые обвиваются вокруг контура и пересекают натянутую поверхность один раз, учитываются в этой сумме.
Слайд 19
Если каждый молекулярный ток равен I m, а площадь его контура S m, то элемент контура L обвивают те молекулярные токи, центры которых попадают внутрь косого цилиндра объемом
Слайд 20
Эти токи пересекают поверхность S один раз, и их вклад в общий ток: где p m = I m S m магнитный момент отдельного молекулярного тока, I m S m n магнитный момент единицы объема, n – концентрация молекул магнетика.
Слайд 21
Проинтегрировав полученное выражение по всему контуру L, получим теорему о циркуляции намагниченности в интегральной форме (6. 5 ) Дифференциальная теорема о циркуляции намагниченности (6.6)
Слайд 22
Циркуляция вектора магнитной индукции по замкнутому контуру в магнитной среде рассчитывается с учетом токов проводимости I и намагничивания I ´, охватываемых контуром L : (6.7)
Слайд 23
С учетом (6.4) теоремы о циркуляции получаем В правой части стоит величина тока проводимости I, не связанная с молекулярной структурой вещества. Вектор напряженности магнитного поля (6.8)
Слайд 24
Тогда теорема о циркуляции вектора напряженности магнитного поля : (6.9) циркуляция вектора по произвольному замкнутому контуру равна сумме токов проводимости, охватываемых этим контуром. дифференциальная (6.10) интегральная
Из (6.3) и (6.8) (6.11)
Слайд 26
Из опыта для парамагнетиков и диамагнетиков (6.12) где χ магнитная восприимчивость среды (может быть и >0, и <0). Для магнетиков, подчиняющихся (6.12), из (6.11) индукция магнитного поля в веществе где μ магнитная проницаемость вещества: (6.13)
Слайд 27
Для однородного изотропного магнетика (6.14) Покажем, используя (6.8) и (6.3), что вектор напряженности магнитного поля одинаков при наличии магнетика и в отсутствие магнетика вектор напряженности магнитного поля в отсутствие магнетика, создан внешними макротоками проводимости.
Слайд 28
Вектор магнитной индукции в магнетике Найдем поле внутри прямого соленоида длиной l с током I и n витков на единицу длины (внутри соленоида вакуум) где N количество витков соленоида. Магнитная индукция в нем
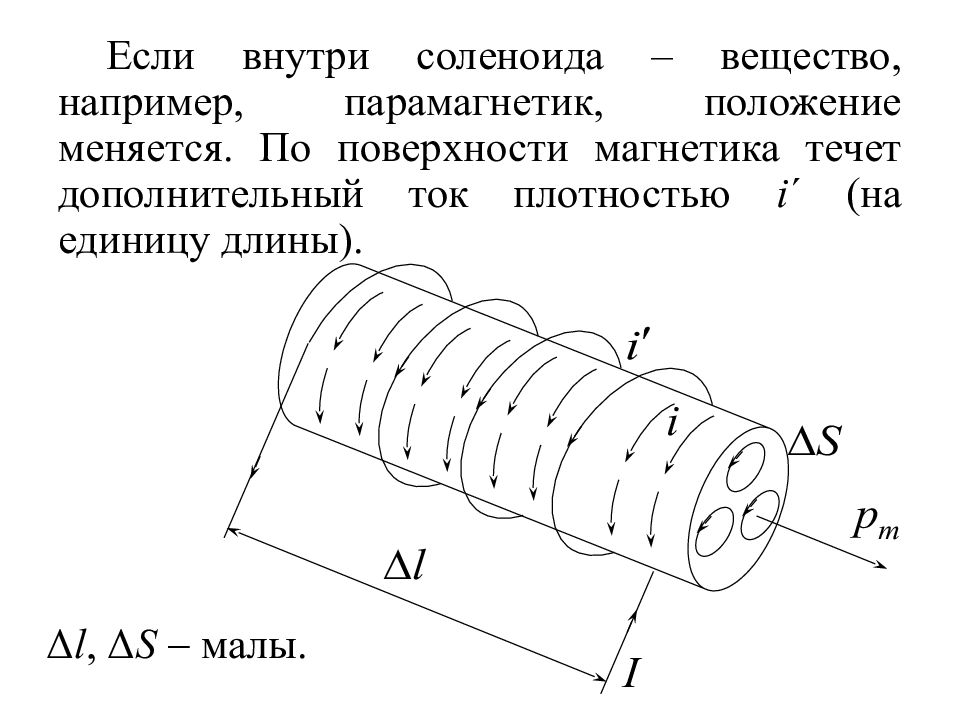
Слайд 29
Если внутри соленоида – вещество, например, парамагнетик, положение меняется. По поверхности магнетика течет дополнительный ток плотностью i ´ (на единицу длины). Δ l, Δ S малы.
Слайд 30
сила поверхностного тока, i ´ линейная плотность поверхностного тока, А/м. Величина магнитного момента элементарного цилиндра из парамагнетика Здесь Намагниченность (11.15)
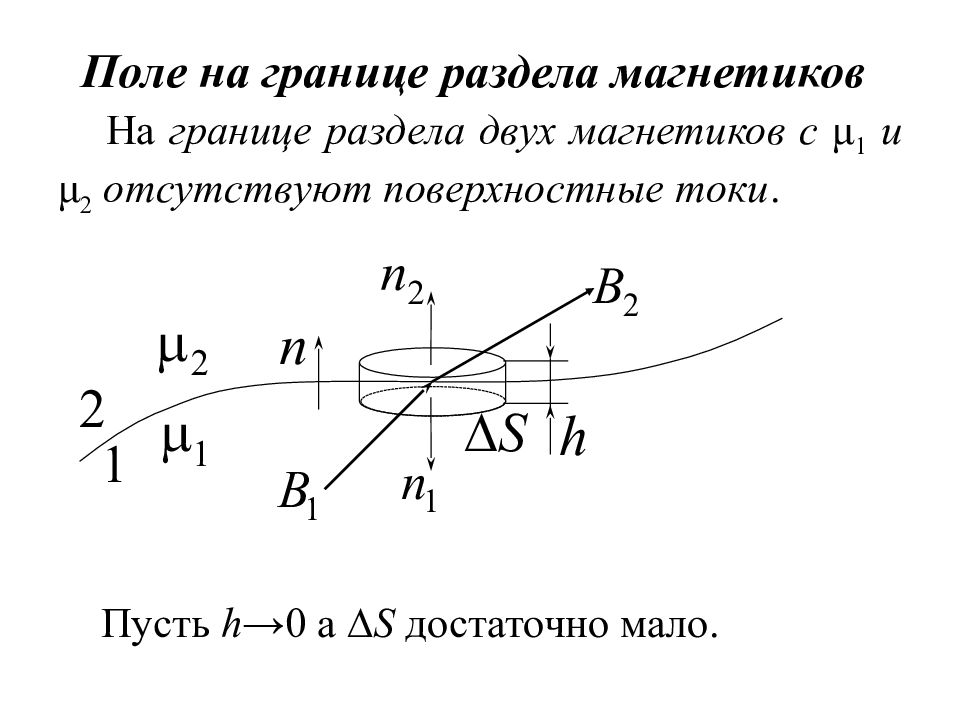
Слайд 31: Поле на границе раздела магнетиков
На границе раздела двух магнетиков с μ 1 и μ 2 отсутствуют поверхностные токи. Пусть h →0 а S достаточно мало.
Слайд 32
Теорема Гаусса: (11.16) (11.17) В рассматриваемых магнетиках Тогда из (11.17): (11.18)
Слайд 33
Контур длины l (достаточно малой) и Теорема о циркуляции (6.19) (6.20) (6.21) ширины h →0.
Слайд 34
Вблизи границы раздела (6.22) Тогда с учетом ГУ и (6.23) из (6.22) (6.24)
Слайд 35: Диамагнетики и парамагнетики
Диамагнетики. μ < 1, χ < 0. χ ~ – 10 – 6 – медь ( Cu ), ртуть ( Hg ); малочисленный класс веществ. намагниченность диамагнетика при
Слайд 36
При помещении диамагнетика во внешнее магнитное поле появляется Намагниченность – против поля, Наличие диамагнетика уменьшает магнитную индукцию.
Слайд 37
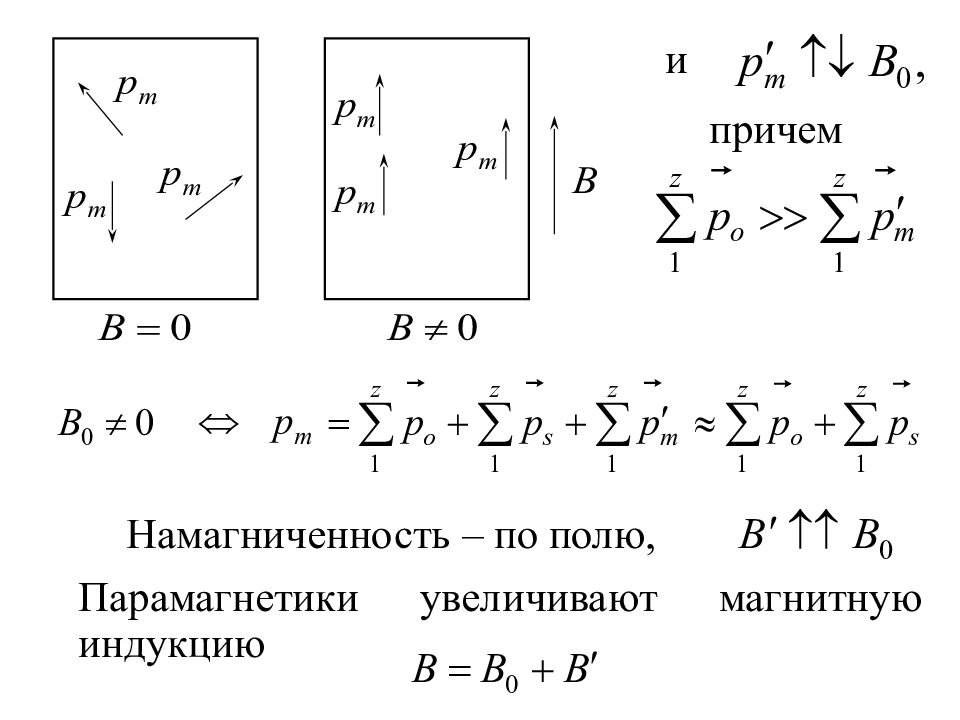
Парамагнетики. μ > 1, χ > 0. χ ~ +10 – 6 – калий ( K ), натрий ( Na ); многочисленный класс веществ. В отсутствие внешнего магнитного поля его атомы (молекулы) обладают магнитным моментом Вследствие хаотической ориентации магнитных моментов, намагниченность парамагнетика при орбитальные моменты молекул парамагнетика стремятся расположиться по полю При появляется
Слайд 38
и причем Намагниченность – по полю, Парамагнетики увеличивают магнитную индукцию
Слайд 39: Ферромагнетики
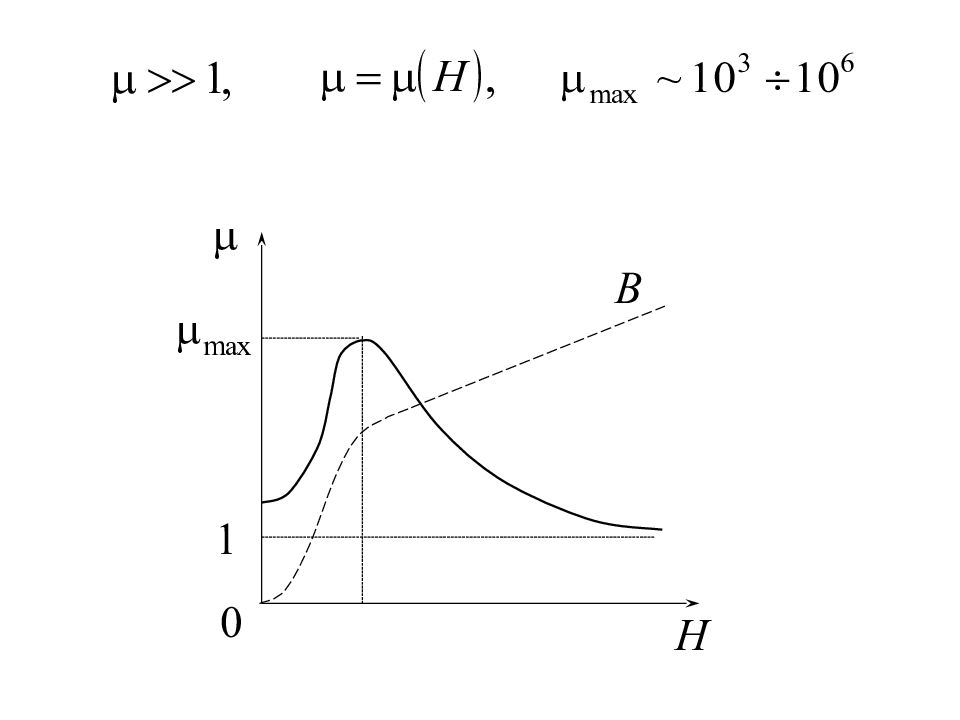
Ферромагнетики – твердые вещества, которые могут обладать спонтанной намагниченностью, т.е. намагничены уже при отсутствии внешнего магнитного поля – железо ( Fe ), кобальт ( Co ), никель ( Ni ), сплавы, самый малочисленный класс веществ, занимают особое место среди магнетиков. Характерная особенность ферромагнетиков – сложная нелинейная зависимость или
Слайд 40
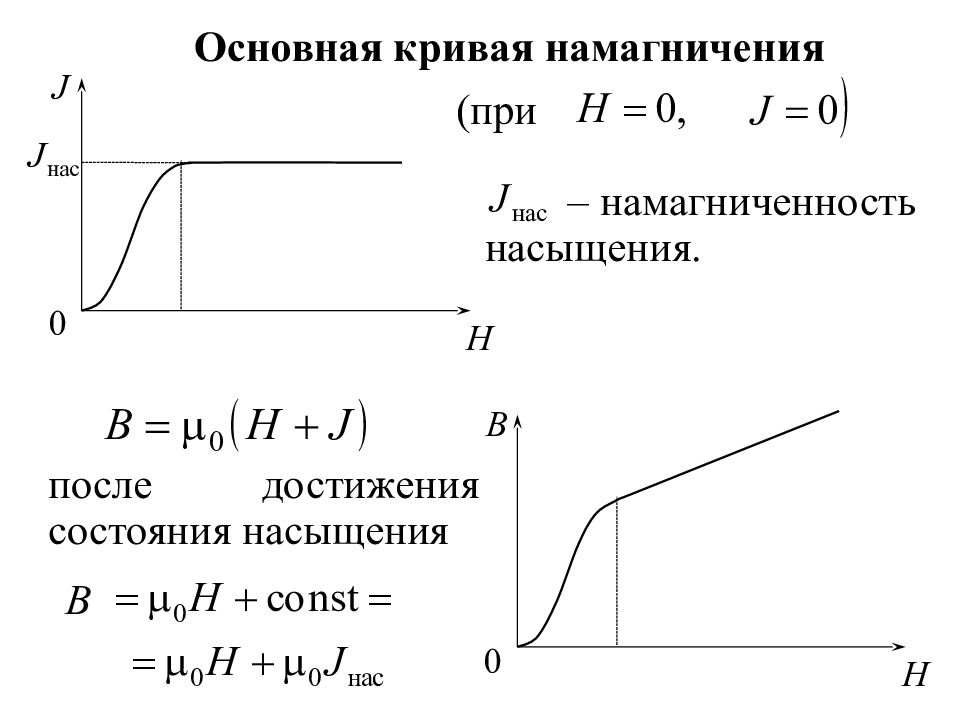
Основная кривая намагничения (при – намагниченность насыщения. после достижения состояния насыщения
Слайд 42
Ферромагнетики состоят из доменов. При определенных условиях в кристаллах могут возникать обменные силы, которые заставляют магнитные моменты электронов устанавливаться параллельно друг другу. В результате возникают домены – области спонтанного (самопроизвольного) намагничивания. Размер домена ~ 1 ÷ 10 мкм. В пределах каждого домена ферромагнетик намагничен до насыщения и при имеет определенный магнитный момент.
Слайд 43
причем B ´ достигает больших величин. Ферромагнетики существенно увеличивают магнитную индукцию. При помещении ферромагнетика во внешнее магнитное поле, домены располагаются по полю Вследствие хаотической ориентации доменов, суммарный момент образца равен нулю и образец в целом оказывается макроскопически ненамагниченным
Слайд 44
Связь между B и H или J и H в ферромагнетике неоднозначна и определяется предшествующей историей его намагничивания – наблюдается магнитный гистерезис. Ферромагнетики и парамагнетики ведут себя в магнитном поле сходным образом. Отличие – доменное строение ферромагнетиков.
Слайд 45
01 – основная кривая намагничения, замкнутая кривая – петля гистерезиса. Если в т. 1 и 4 достигается насыщение – максимальная петля гистерезиса. Т. 2 характеризуется B r – остаточной индукцией, ей соответствует остаточная намагниченность J r. B ( H c ) (т. 3 ) обращается в нуль под действием поля H c, ↑↓ полю, вызвавшему намагничивание. H c – коэрцитивная сила.
Слайд 46
Для разных ферромагнетиков B r и H c меняются в широких пределах. В парамагнетике – существует остаточная намагниченность, но она значительно слабее. В диамагнетике остаточной намагниченности нет, поскольку прецессионное движение прекращается сразу же при выключении магнитного поля. С наличием остаточного намагничивания связано существование постоянных магнитов.
Слайд 47
При повышении температуры способность ферромагнетиков намагничиваться уменьшается, в частности, уменьшается намагниченность насыщения. Точка Кюри (температура Кюри) – температура, при которой магнитные свойства ферромагнетика исчезают. При температурах, более высоких, чем температура Кюри, домены под действием теплового движения разрушаются и ферромагнетик превращается в парамагнетик. Для железа точка Кюри равна 753 ° С.
Слайд 48
Также размагнитить ферромагнетик можно, встряхнув (механическим ударом нарушив ориентацию доменов). Также помещают намагниченный образец из ферромагнетика в катушку (внутрь длинного соленоида) с переменным током и амплитуду тока постепенно уменьшают до нуля. При этом ферромагнетик подвергается многократным циклическим перемагничиваниям, в которых петли гистерезиса постепенно уменьшаются (уменьшая амплитуду H ), стягиваясь к точке O, где намагниченность равна нулю.
Последний слайд презентации: Лекция № 6
При перемагничивании ферромагнетик нагревается, при этом в единице объема ферромагнетика выделяется теплота Q y, численно равная «площади» S n петли гистерезиса: Мягкие ферромагнетики (с меньшей площадью петли гистерезиса) легко перемагничиваются, жесткие ферромагнетики (с большей площадью петли гистерезиса) – для создания постоянных магнитов.