Первый слайд презентации
ЛЕКЦИЯ №1 Основные положения механики деформированного тела
Слайд 2
План лекции: Сопротивление материалов как наука. Основные понятия и определения 2. Понятие расчетной схемы. Расчетные формы и их классификация 3. Классификация и схематизация сил и форм тела. Понятие о расчетной схеме 4. Внутренние силы. Метод сечений 5. Напряжение полное, нормальное, касательное 6. Деформации и перемещения 7. Гипотезы и допущения механики деформированного тела
Слайд 3
Основные понятия сопромата Прикладная наука об инженерных методах расчёта на прочность, жесткость и устойчивость деталей машин и конструкций, называется сопротивлением материалов. Деталь или конструкция называется прочной, если под действием внешних сил в ней не возникает значительных пластических деформаций, или она не разрушается (не распадается на две или более частей). Деталь или конструкция называется жесткой, если упругие деформации, возникающие в ней под действием приложенных сил, не оказывают существенного влияния на ее работу. Конструкция или деталь называется устойчивой, если в результате действия на нее заданных нагрузок она сохраняет первоначальную форму упругого равновесия. Основной задачей сопротивления материалов является разработка методов расчета на прочность, жесткость и устойчивость с целью получения надежных и экономически обоснованных размеров элементов конструкций
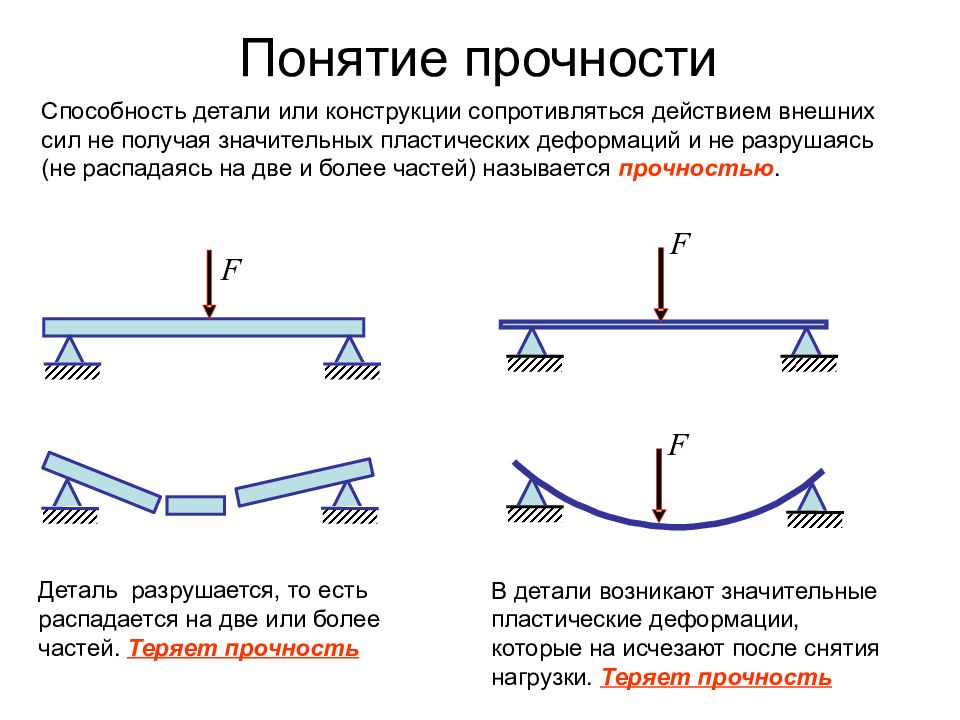
Слайд 4: Понятие прочности
F F F Деталь разрушается, то есть распадается на две или более частей. Теряет прочность В детали возникают значительные пластические деформации, которые на исчезают после снятия нагрузки. Теряет прочность Способность детали или конструкции сопротивляться действием внешних сил не получая значительных пластических деформаций и не разрушаясь (не распадаясь на две и более частей) называется прочностью.
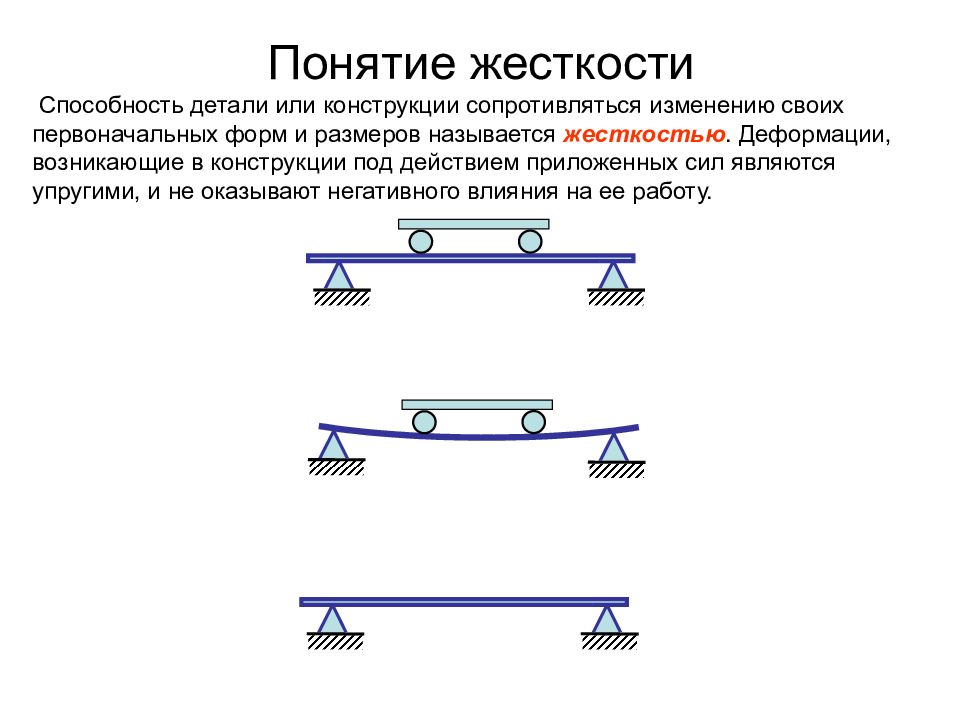
Слайд 5: Понятие жесткости
Способность детали или конструкции сопротивляться изменению своих первоначальных форм и размеров называется жесткостью. Деформации, возникающие в конструкции под действием приложенных сил являются упругими, и не оказывают негативного влияния на ее работу.
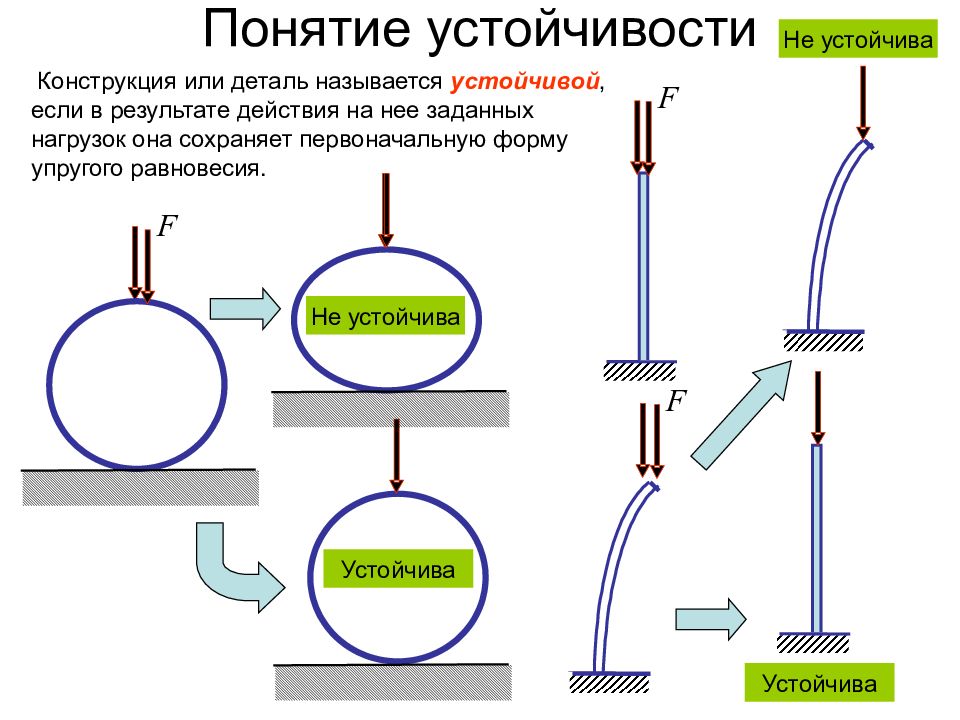
Слайд 6: Понятие устойчивости
F Конструкция или деталь называется устойчивой, если в результате действия на нее заданных нагрузок она сохраняет первоначальную форму упругого равновесия. Не устойчива Устойчива F F Устойчива Не устойчива
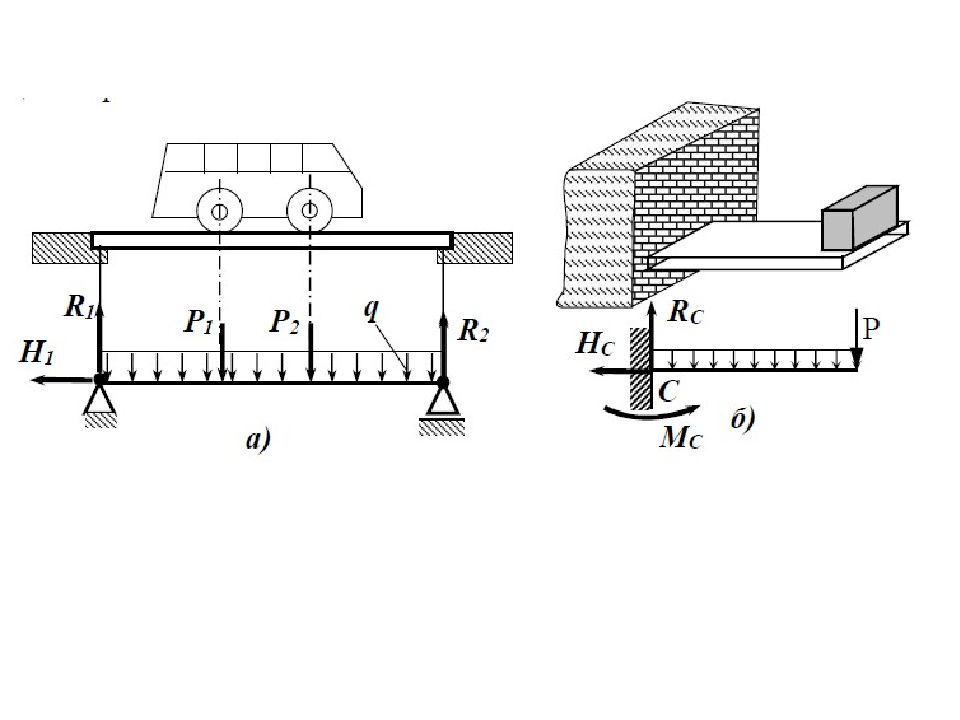
Слайд 9: Понятие расчетной схемы
Условное изображение конструкции или детали принимаемое для выполнения расчета, называется расчетной схемой. Расчетная схема выбирается так, чтобы существенно упростить расчет, не искажая действительной картины работы конструкции или детали Расчетную схему составляют в следующем порядке: Разбивают конструкцию на простые элементы Каждый простой элемент конструкции заменяют соответствующим расчетным элементом (брусом, пластиной, оболочкой, массивным телом); Выбирают схему опорных частей элемента или конструкции (подвижный и неподвижный шарнир, жесткая заделка и другие); Выбирают вариант соединения элементов конструкции между собой и с опорными частями (жесткий или шарнирный).
Слайд 12: Расчетные формы и их классификация
Брусом называется расчетный элемент, длина которого значительно больше размеров его поперечного сечения. Брусья классифицируются по форме поперечного сечения и форме оси. По форме поперечного сечения различают брусья постоянного сечения и переменного сечения. По форме оси – прямолинейные и криволинейные брусья. Примерами прямых брусьев являются балки и стержни мостовых и козловых кранов, валы редукторов и коробок передач, оси транспортных средств. Примерами кривых брусьев служат грузоподъёмные крюки, звенья сварных цепей, струбцины, коленчатые валы, станины станков.
Слайд 13: Расчетные формы и их классификация
Оболочкой называется элемент произвольной формы, длина и ширина которого во много раз превышает его толщину. Оболочки могут иметь цилиндрическую, коническую или сферическую форму. Оболочка, срединная поверхность которой представляет собой плоскость, называется пластинкой. Встречаются пластинки прямоугольные и круглые.
Слайд 14
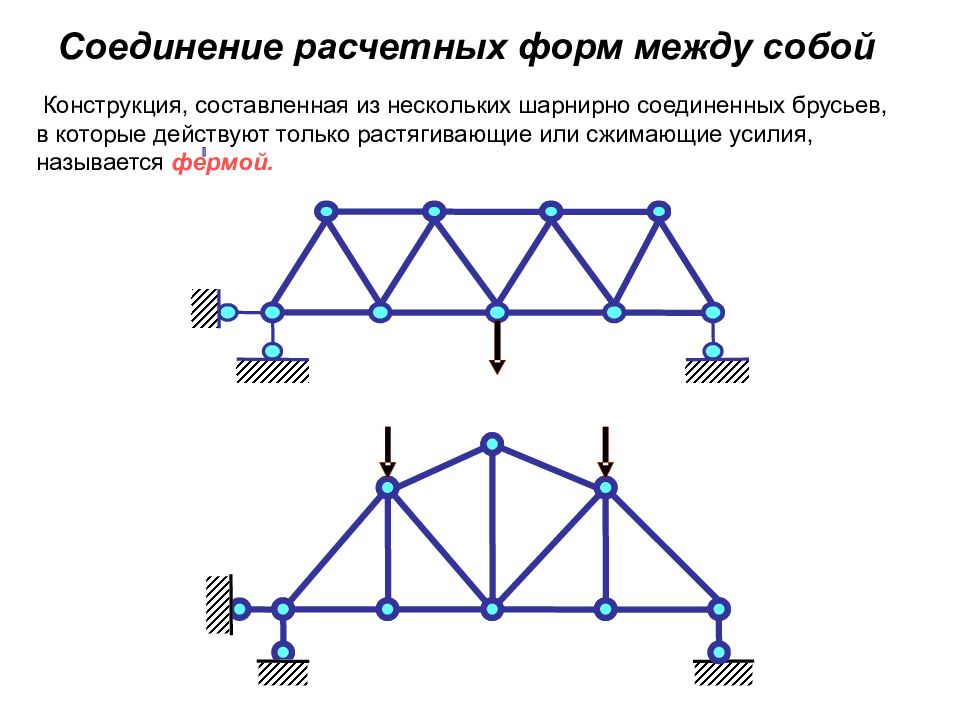
Соединение расчетных форм между собой Конструкция, составленная из нескольких шарнирно соединенных брусьев, в которые действуют только растягивающие или сжимающие усилия, называется фермой.
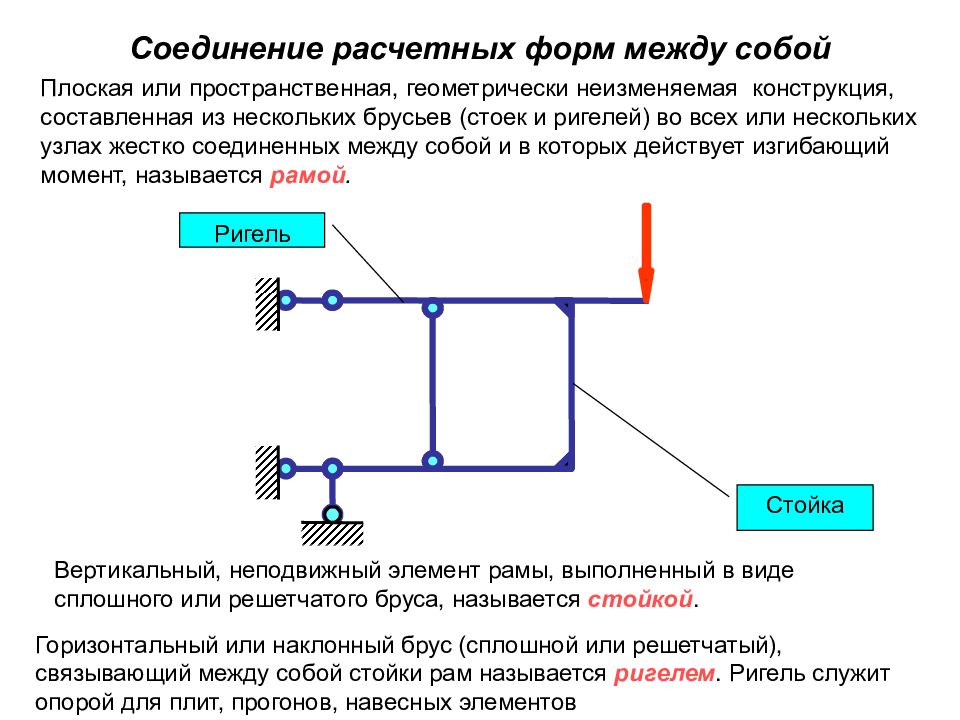
Слайд 15: Соединение расчетных форм между собой
Плоская или пространственная, геометрически неизменяемая конструкция, составленная из нескольких брусьев (стоек и ригелей) во всех или нескольких узлах жестко соединенных между собой и в которых действует изгибающий момент, называется рамой. Вертикальный, неподвижный элемент рамы, выполненный в виде сплошного или решетчатого бруса, называется стойкой. Горизонтальный или наклонный брус (сплошной или решетчатый), связывающий между собой стойки рам называется ригелем. Ригель служит опорой для плит, прогонов, навесных элементов Ригель Стойка
Слайд 16
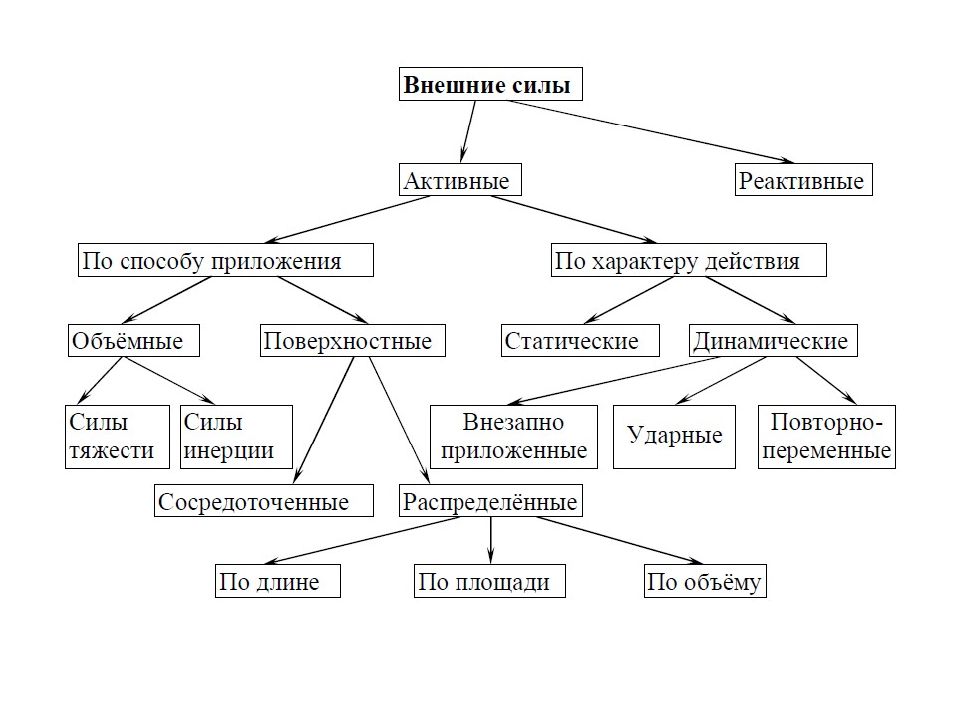
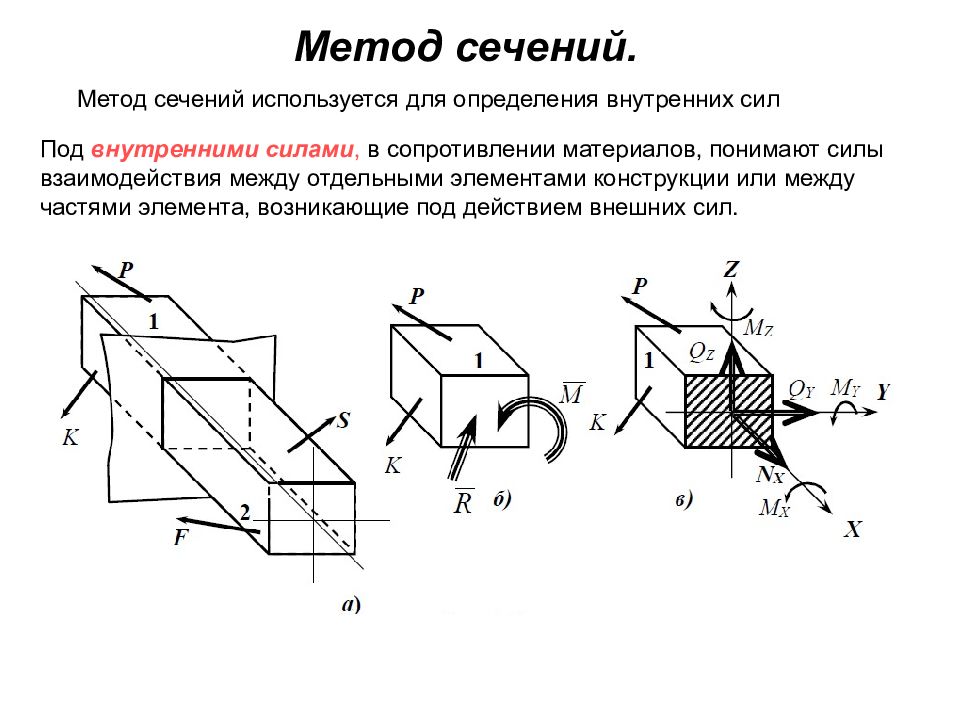
Метод сечений. Метод сечений используется для определения внутренних сил Под внутренними силами, в сопротивлении материалов, понимают силы взаимодействия между отдельными элементами конструкции или между частями элемента, возникающие под действием внешних сил.
Слайд 18: Понятие напряжения
d R d N d Q d A F 1 F n F 2 p d A F 1 F n F 2 Полным механическим напряжением называют отношение равнодействующей внутренних сил dR действующей на малый элемент выбранного сечения к площади этого элемента dA. Нормальным напряжением называется отношение нормальных сил dN действующих на малый элемент выбранного сечения к площади этого сечения dA : Касательным напряжением называется отношение касательных сил dQ действующих на малый элемент выбранного сечения к площади dA этого элемента. Нормальные и касательные напряжения являются составляющими полного напряжения р:
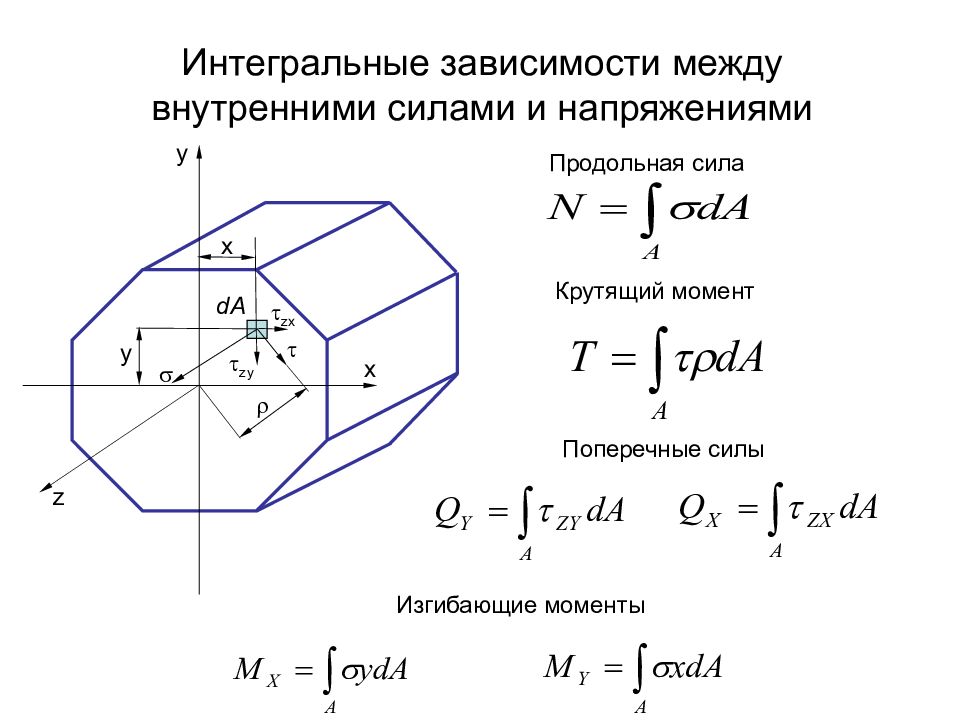
Слайд 19: Интегральные зависимости между внутренними силами и напряжениями
Продольная сила Крутящий момент Поперечные силы Изгибающие моменты dA y x z zx y zy x
Слайд 20: Деформации и перемещения
D a а в F Изменение формы и размеров тела в результате действия внешних нагрузок, называется деформацией. Любая деформация элементов тела может быть разложена на два вида элементарных деформаций: линейные и угловые. Приращение длины ребра бруса после деформации а ( в ) называется абсолютным удлинением (укорочением). Мерой линейной продольной деформации является относительное удлинение, , которое равно отношению абсолютного удлинения бруса, а к начальному размеру а : в /2 Линейными называются деформации, при которых происходит изменение линейных размеров бруса, а все угловые соотношения остаются неизменными.
Слайд 21: Деформации и перемещения
а а F g s D Угловыми называются деформации, при которых изменяются углы между ребрами бруса за счет сдвига одной плоскости элемента относительно другой. Величина перемещения любой точки в плоскости сдвига s, называется абсолютным сдвигом. Мерой угловой деформации является относительный сдвиг, , который равен отношению абсолютного сдвига s к расстоянию между плоскостями сдвига а :
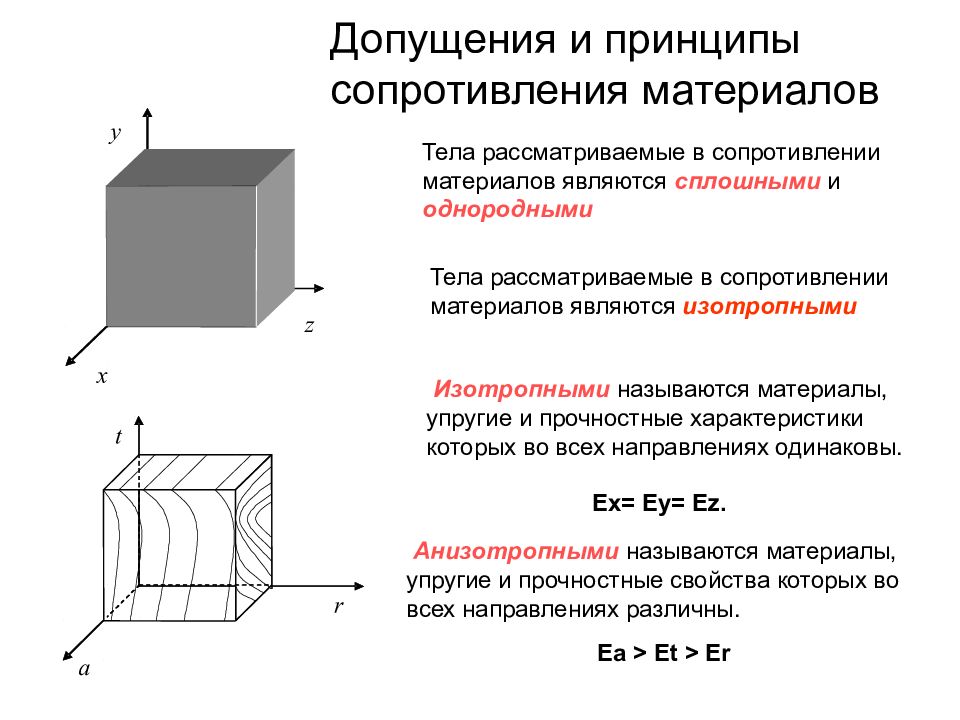
Слайд 22: Допущения и принципы сопротивления материалов
Изотропными называются материалы, упругие и прочностные характеристики которых во всех направлениях одинаковы. Анизотропными называются материалы, упругие и прочностные свойства которых во всех направлениях различны. y z x r t a Еx= Еy= Еz. Еа > Еt > Еr Тела рассматриваемые в сопротивлении материалов являются сплошными и однородными Тела рассматриваемые в сопротивлении материалов являются изотропными
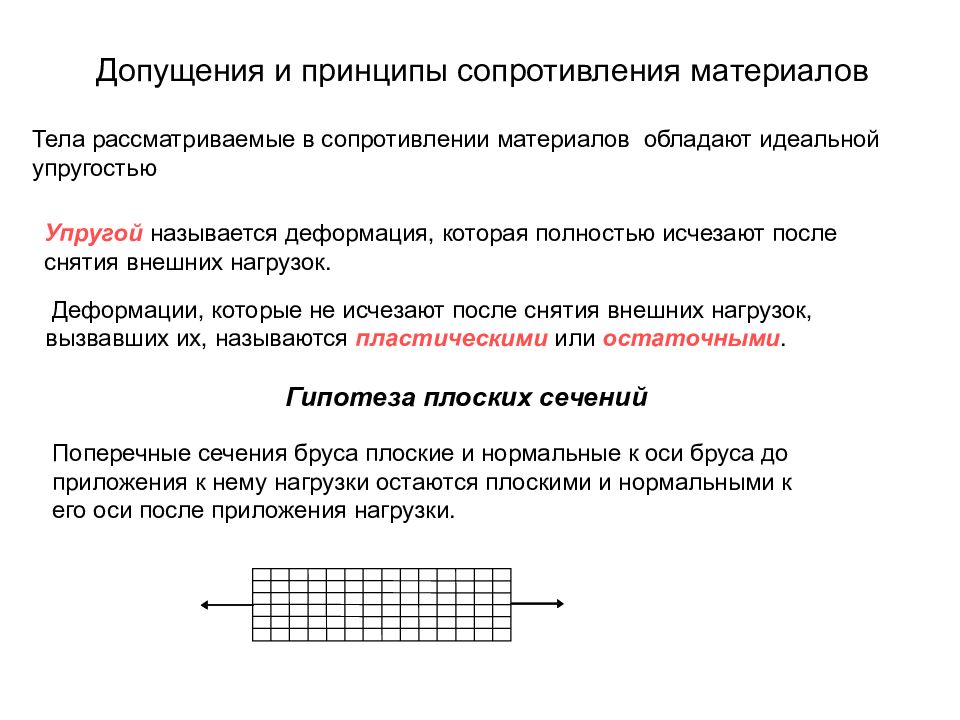
Слайд 23: Допущения и принципы сопротивления материалов
Упругой называется деформация, которая полностью исчезают после снятия внешних нагрузок. Деформации, которые не исчезают после снятия внешних нагрузок, вызвавших их, называются пластическими или остаточными. Тела рассматриваемые в сопротивлении материалов обладают идеальной упругостью Поперечные сечения бруса плоские и нормальные к оси бруса до приложения к нему нагрузки остаются плоскими и нормальными к его оси после приложения нагрузки. Гипотеза плоских сечений
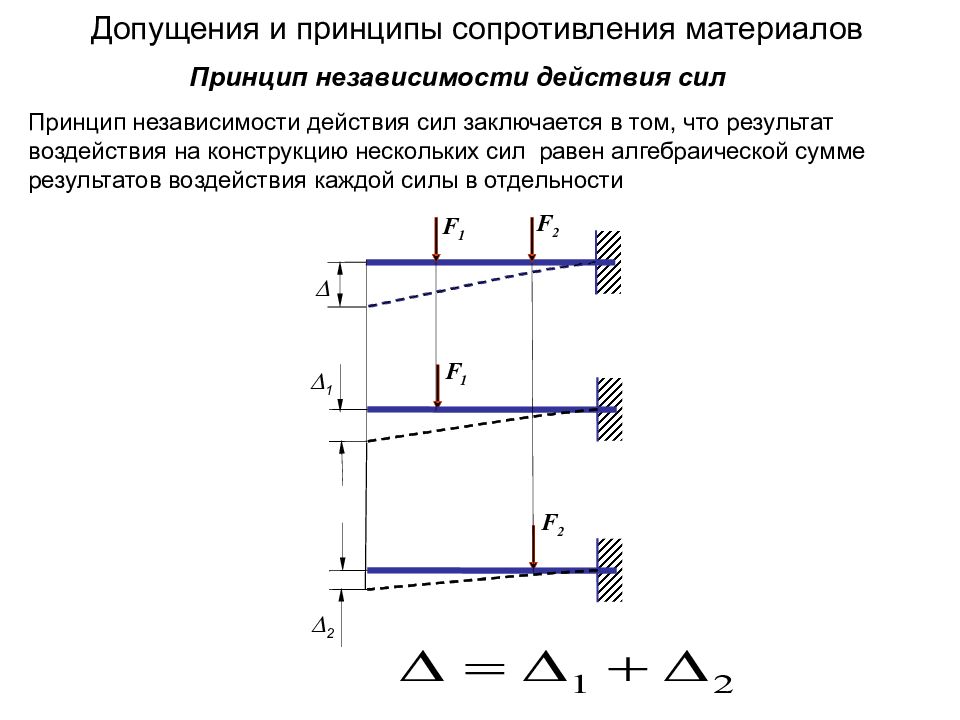
Слайд 24: Допущения и принципы сопротивления материалов
Принцип независимости действия сил заключается в том, что результат воздействия на конструкцию нескольких сил равен алгебраической сумме результатов воздействия каждой силы в отдельности Принцип независимости действия сил F 1 F 2 F 2 F 1 D D 2 D 1
Слайд 25: Допущения и принципы сопротивления материалов
F l l l 2F l Гипотеза Гука Деформации материала в каждой его точке прямо пропорциональны напряжениям в этой точке.
Последний слайд презентации: ЛЕКЦИЯ №1 Основные положения механики деформированного тела: Допущения и принципы сопротивления материалов
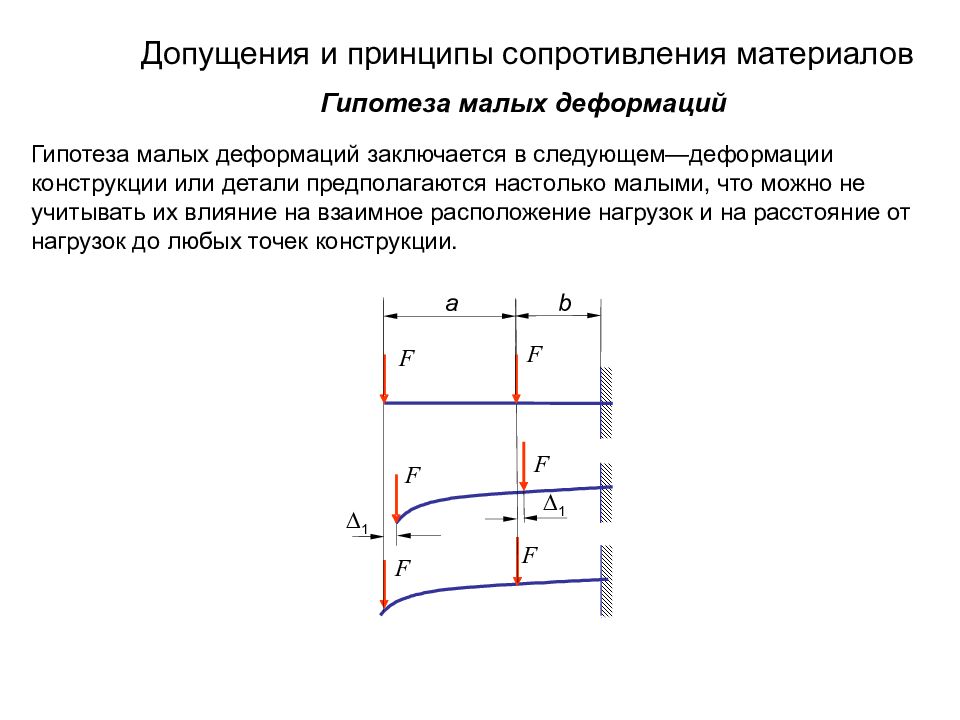
F F F F 1 1 F F a b Гипотеза малых деформаций Гипотеза малых деформаций заключается в следующем—деформации конструкции или детали предполагаются настолько малыми, что можно не учитывать их влияние на взаимное расположение нагрузок и на расстояние от нагрузок до любых точек конструкции.