Рогожин В.Б. к.ф.-м.н. ЛЕКЦИЯ 3 Разбавленные растворы Основы физики полимеров и жидких кристаллов
(2-й закон Фика)
- сдвиговая вязкость растворителя. Основанный на этих выводах метод определения D носит название метода изотермической диффузии. где - константа, зависящая от граничных условий, - средний квадрат смещения броуновской частицы в растворе. Сам по себе коэффициент диффузии позволяет нам получить размер полимерного клубка. К примеру, если клубки рассматривать как непротекаемые сферы, то их гидродинамический радиус можно определить по формуле Стокса:
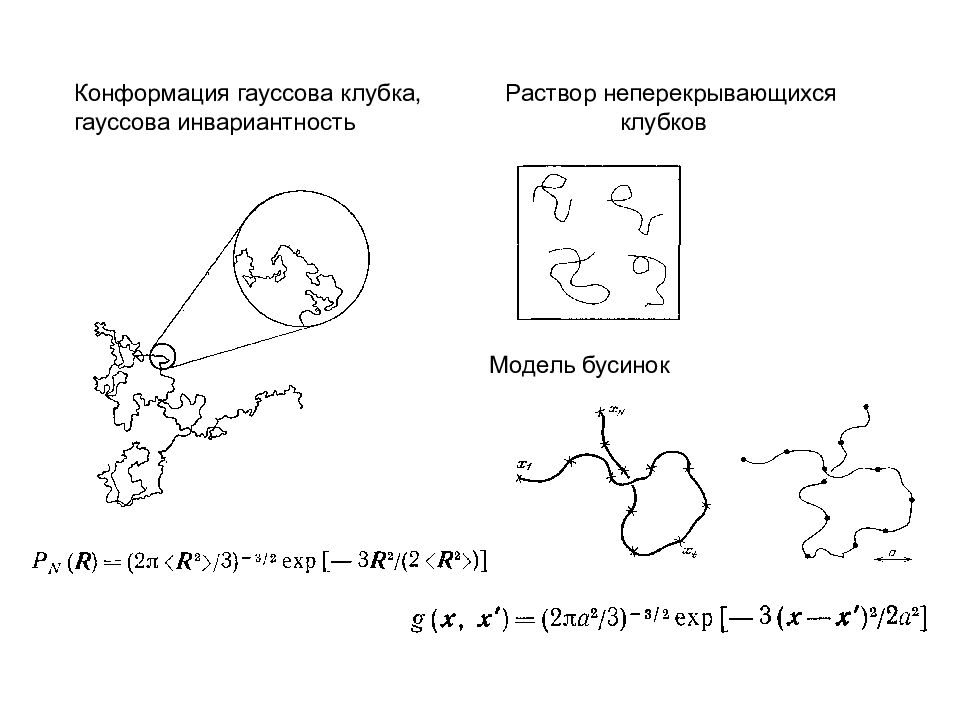
Раствор неперекрывающихся клубков Конформация гауссова клубка, гауссова инвариантность Модель бусинок
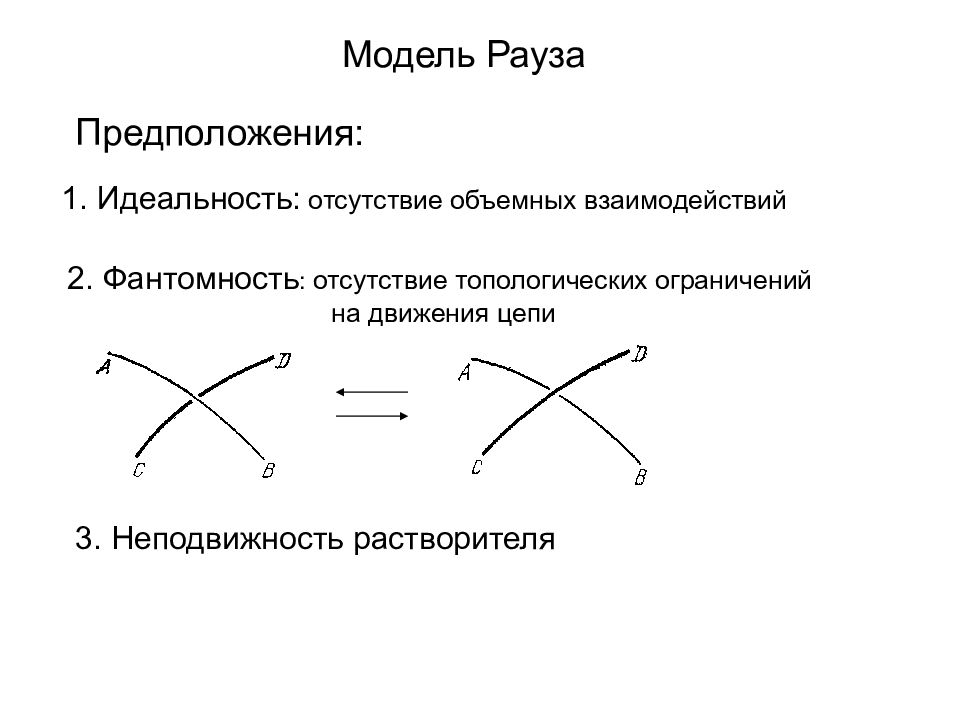
Модель Рауза 1. Идеальность: отсутствие объемных взаимодействий 2. Фантомность : отсутствие топологических ограничений на движения цепи 3. Неподвижность растворителя
Уравнение движения: - сила, действующая со стороны соседних звеньев - сила трения о растворитель случайная сила, возникающая за счет столкновений между звеньями цепи и молекулами растворителя Энергия взаимодействия звеньев полная энергия взаимодействия N – число звеньев цепи
где - коэффициент трения о растворитель - нулевое среднее значение - дельта-коррелированность - уравнение Ланжевена Для первого и N - го звена: Для придания этим двум уравнениям общего вида уравнения движения введем нулевое и N+ 1 звено:
- линейное дифференциальное уравнение второго порядка типа уравнения диффузии - граничные условия Тогда в континуальном пределе n можно считать величиной непрерывной: при больших N медленно меняются с аргументами по длине цепи.
Ищем решение в виде: Обратное преобразование Фурье: 6 времена релаксации раузовских мод для участков цепи из N/p звеньев - положение центра масс клубка полимерной цепи - коэффициент диффузии для клубка - коэффициент диффузии для мономерного звена Совокупность независимых уравнений для релаксационных, или раузовских мод
для времени релаксации первой раузовской моды и коэффициента диффузии клубка - для -растворителя - учет поля скоростей растворителя в силе трения - стоксовский коэффициент диффузии для непротекаемого шара радиусом R Для -растворителя: , тогда - оценка верна. Уравнение Навье –Стокса: где p ( x ) – давление, - внешняя сила в расчете на единицу объема, действующая на растворитель вблизи точки х Растворитель – несжимаемая вязкая жидкость, возмущение жидкости слабое (малые числа Рейнольдса). Тогда: Но полученные в рамках модели зависимости не отвечают эксперименту : Причина: не учитывается увлечение звеньями растворителя. Это исправляется в модели Зимма: Оценка:
- тензор Озеена, Уравнение Зимма: В приближении предварительного усреднения по равновесной функции распределения: где: - гидродинамический радиус непротекаемого клубка
Учет объемных взаимодействий Типичный вид реального потенциала взаимодействия Распределение функции плотности вероятности, рассчитанное с учетом объемных взаимодействий, сплошная линия (пунктир – гауссова функция распределения) m, n >>1 Для где - критический показатель проблемы исключенного объема где - пространственный размер полимерного клубка с исключенным объемом
