Кредитные расчеты
Кредит (от лат. credit — он верит) — это предоставление кредитором заемщику определенной суммы средств (в денежной или товарной форме) на условиях платности, срочности, возвратности и обеспеченности (в РФ — залог, банковская гарантия, поручительство, страховая ответственность заемщика за погашение кредита). Кредитные операции делятся на активные (банк или другой хозяйствующий субъект выдает ссуды) и пассивные (банк или другой хозяйствующий субъект берет ссуды). Кредитные операции могут осуществляться в двух формах — в форме ссуд и в форме депозитов.
Банковское кредитование подразделяется на прямое и косвенное. Прямое кредитование — это кредитные отношения хозяйствующих субъектов непосредственно с банком. Косвенное кредитование означает, что кредитные отношения возникают вначале между хозяйствующими субъектами, которые впоследствии обращаются в банк за кредитами. Основными видами косвенного банковского кредитования выступают операции с векселями, факторинг и лизинг.
Различают следующие основные формы кредита: краткосрочный, выдаваемый, как правило, на срок до года, предназначенный преимущественно для формирования оборотных средств предприятий, фирм; долгосрочный, предоставляемый на срок свыше года и используемый в основном в качестве инвестиционного капитала; гарантированный, предоставляемый под гарантию, под обеспечение; государственный, в котором в качестве заемщика выступает государство, а в роли кредитора — физические и юридические лица, приобретающие государственные ценные бумаги (облигации, казначейские сертификаты и др.); банковский, представляемый банками в денежной форме; потребительский, предоставляемый потребителям товаров и услуг и используемый для удовлетворения потребительских нужд.
Цена кредита — ставка банковского процента. В зависимости от кредитной политики банка, сумма процентного платежа может рассчитываться от первоначальной основной суммы кредита или от текущего остатка основной суммы кредита. Первый метод определения банковского вознаграждения уже практически никем не используется, поскольку данный расчет дает конечную сумму процентных выплат почти в 2 раза больше, чем метод вычисления от остаточной суммы. Ставка (процент) банковского кредита устанавливается каждым банком в отдельности, с целью покрытия своих расходов на финансовые ресурсы, административных издержек, нормы прибыли и рисков. Каждая процентная ставка включает в себя все эти четыре величины.
Первая величина зависит от межбанковского рынка, либо от стоимости привлеченных депозитных средств, вторая и третья — от рабочих показателей самого банка, а четвертая — от конкретного клиента и структуры займа. Расчет степени риска по кредиту включает в себя рассмотрение платежеспособности, финансового состояния и кредитной истории клиента, характера залога, сроков, формы графика выплат и много другого. Чем ниже степень риска кредитодателя, тем дешевле будут предоставленные средства для клиента.
фиксированная ставка — называется один раз и закрепляется в кредитном договоре вместе с периодом ее актуализации. С учетом периодических пересмотров используется для начисления процентов до окончания срока действия договора. Как правило, фиксированная ставка гораздо выше плавающей, так как включает анализ динамики изменения ставок рефинансирования ЦБ РФ, гарантии рисков инфляции, экономических кризисов, девальвации валюты кредита и т.д. плавающая ставка — состоит из двух частей, фиксированной и меняющейся. Фиксированная часть называется один раз и действует до окончания срока действия кредитного договора. Процентная ставка: фиксированная и плавающая
В задачах по погашению кредита (заема, ссуды, займа) решается одна и та же проблема: «Составить план погашения долга». Разработка которого заключается в составлении графика (расписания) периодических платежей должника. Такие расходы должника обычно называют расходами по обслуживанию долга или, более кратко, срочными уплатами, расходами по займу. Варианты способов погашения разнообразны.
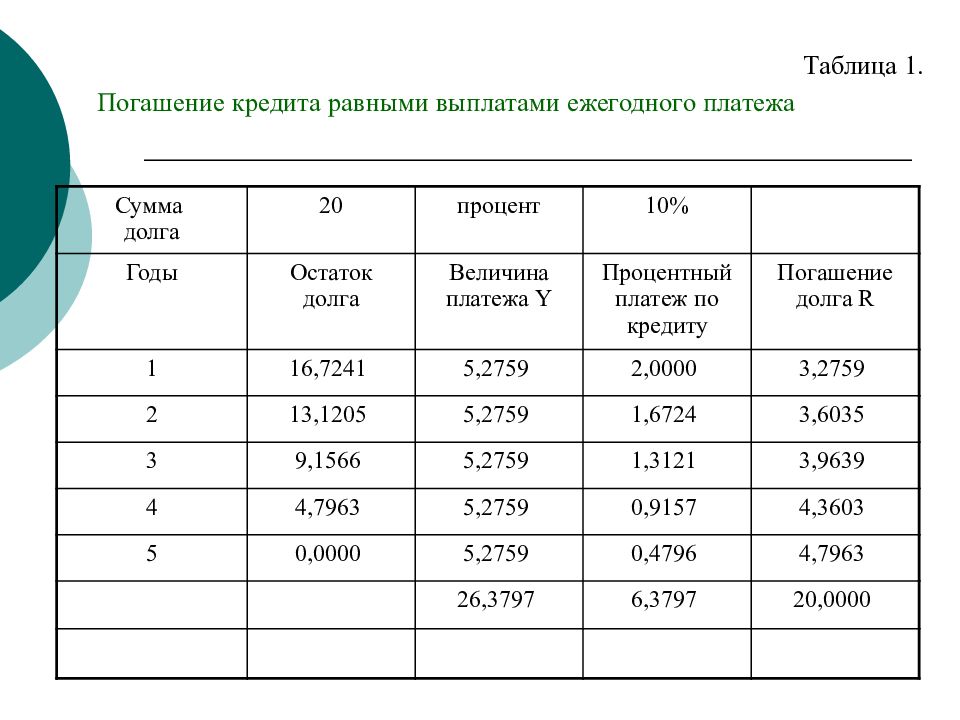
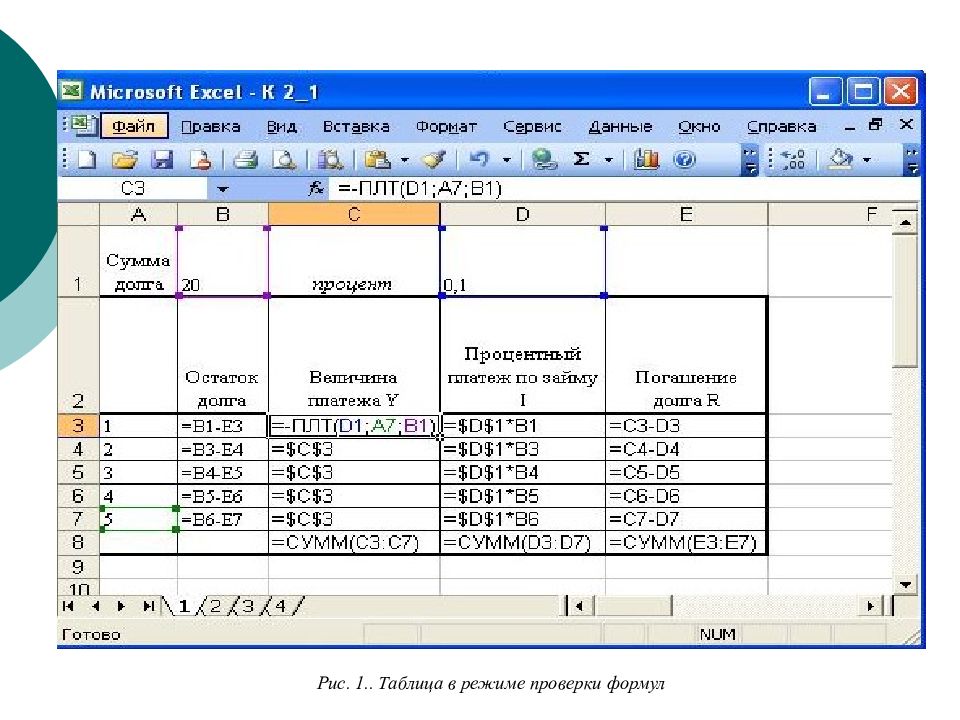
Пример 1.8.1. Пусть следует погасить заем S = 20 млн, выданный на 5 лет под 10% годовых. Погашение осуществлять равными платежами раз в год в конце года. Найти величину платежа. Построить график платежей и остатка долга. Решение. Величина ежегодного (срочного) платежа складывается из двух частей: Y = I + R, где Y – срочная уплата, I —процентный платеж по кредиту, R — расход по погашению основного долга. Используем функцию ПЛТ(ставка ;кпер;пс;бс;тип) Microsoft Excel 2000 для подсчета величины ежегодного платежа. В нашем случае постоянная срочная уплата равна: Y = ПЛТ(10%,1;5;20;0) = -5,2759. Тогда схему погашения кредита можно представить в виде таблицы
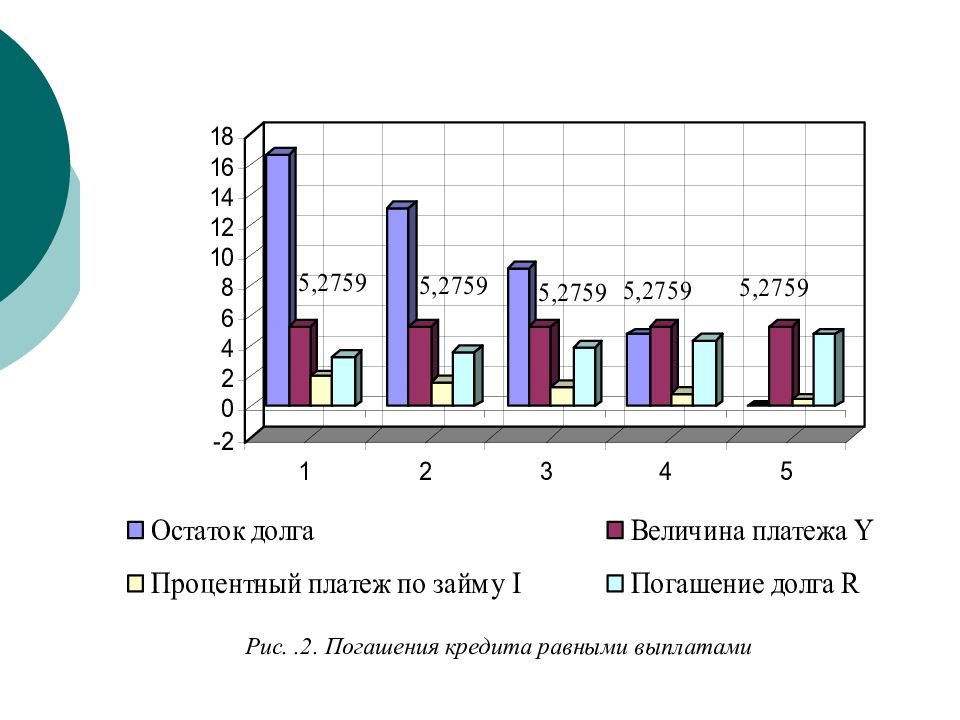
Сумма долга 20 процент 10% Годы Остаток долга Величина платежа Y Процентный платеж по кредиту Погашение долга R 1 16,7241 5,2759 2,0000 3,2759 2 13,1205 5,2759 1,6724 3,6035 3 9,1566 5,2759 1,3121 3,9639 4 4,7963 5,2759 0,9157 4,3603 5 0,0000 5,2759 0,4796 4,7963 26,3797 6,3797 20,0000 Таблица 1. Погашение кредита равными выплатами ежегодного платежа
Рис. 1.. Таблица в режиме проверки формул
Рис..2. Погашения кредита равными выплатами
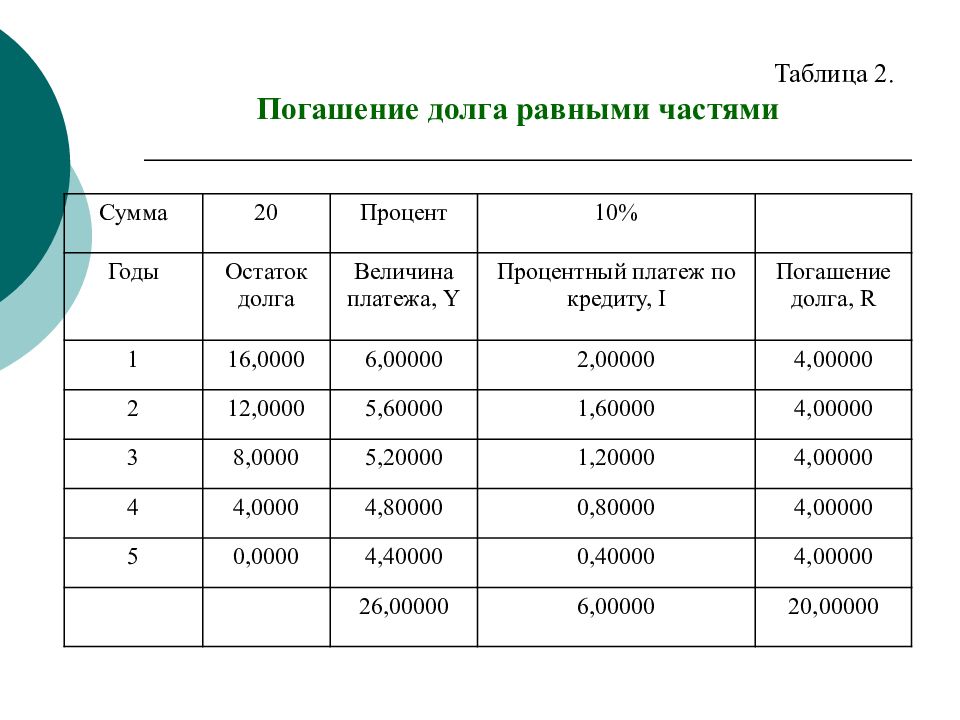
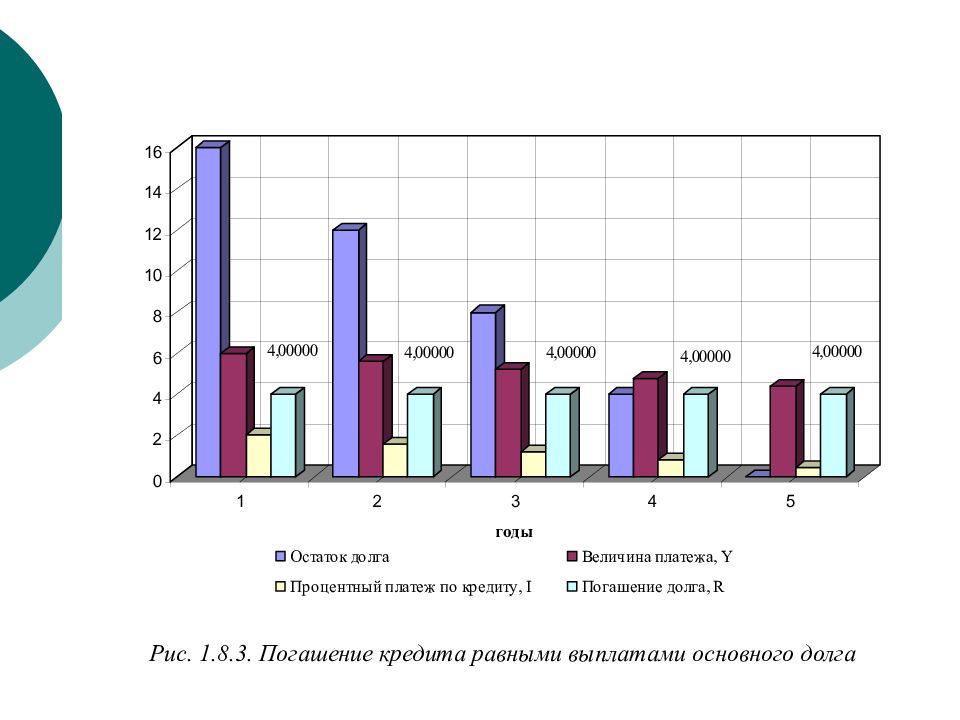
Пример 1.8.2. Кредит в размере 20 тыс. руб. выдан на 5 лет под 10% годовых. Погашение долга должно происходит равными платежами, начисление процента в конце года. Составить план погашения долга. Решение. Найдем годовую уплату долга: R = S / N =20/5=4 тыс. руб. В таблице 2. представлен план погашения кредита равными выплатами основного долга. Погашение кредита равными выплатами основного долга
Сумма 20 Процент 10% Годы Остаток долга Величина платежа, Y Процентный платеж по кредиту, I Погашение долга, R 1 16,0000 6,00000 2,00000 4,00000 2 12,0000 5,60000 1,60000 4,00000 3 8,0000 5,20000 1,20000 4,00000 4 4,0000 4,80000 0,80000 4,00000 5 0,0000 4,40000 0,40000 4,00000 26,00000 6,00000 20,00000 Таблица 2. Погашение долга равными частями
Рис. 1.8.3. Погашение кредита равными выплатами основного долга
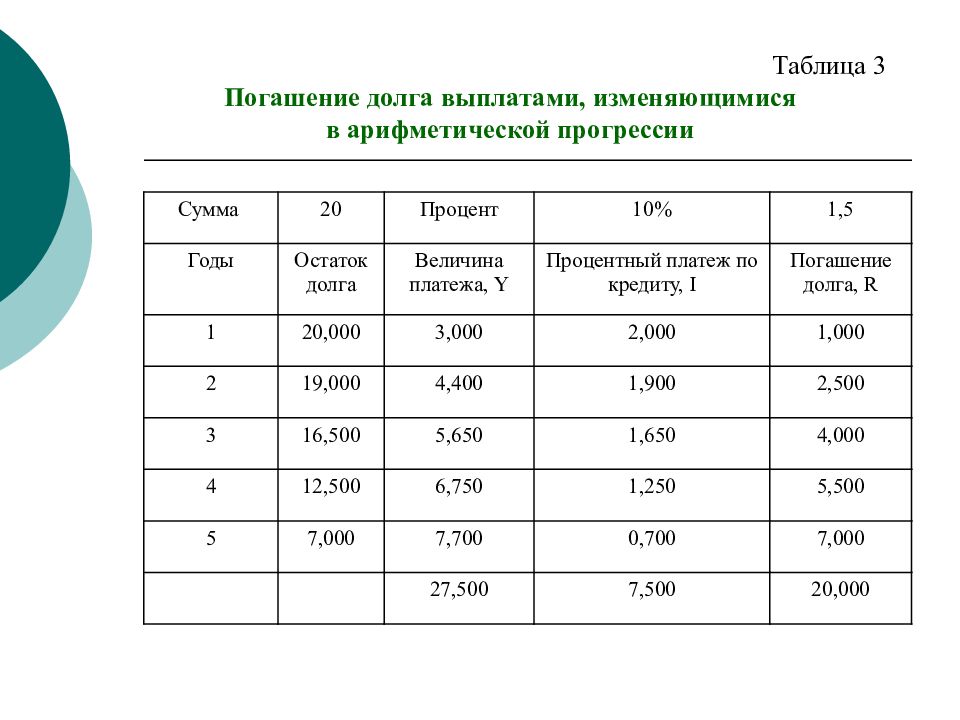
Выплаты изменяются в арифметической прогрессии Пример 3. Кредит в 20 тыс. руб. выдан под 10% годовых на 5 лет. Погашение осуществляется ежегодно, и возрастают в арифметической прогрессии на 1,5 тыс. руб. Начисление процента осуществляется в конце года. Составить схему погашения кредита. Для нахождения постоянной выплаты используем формулу суммы n -членов арифметической прогрессии): (1.8.1) откуда первый член арифметической прогрессии равен: В таблице 1.8.3 представлен план погашения кредита, когда выплаты изменяются в арифметической прогрессии.
Сумма 20 Процент 10% 1,5 Годы Остаток долга Величина платежа, Y Процентный платеж по кредиту, I Погашение долга, R 1 20,000 3,000 2,000 1,000 2 19,000 4,400 1,900 2,500 3 16,500 5,650 1,650 4,000 4 12,500 6,750 1,250 5,500 5 7,000 7,700 0,700 7,000 27,500 7,500 20,000 Таблица 3 Погашение долга выплатами, изменяющимися в арифметической прогрессии
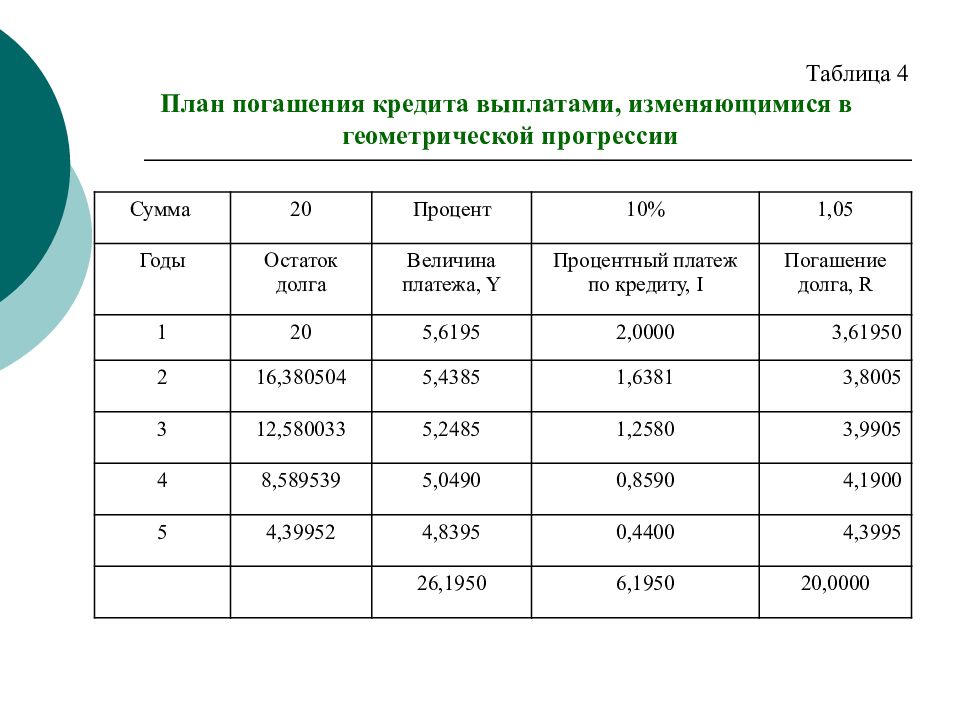
Еще одним из вариантов погашения займа является выплаты в геометрической прогрессии. Пример Кредит в размере 20 тыс. руб. выданный на 5 лет под 10% годовых должен быть погашен ежегодными выплатами. Выплаты, идущие на погашение основного долга должны возрастать в геометрической прогрессии на 5% ежегодно. Составить план погашения кредита. Решение. Постоянная выплата равна (используем формулу суммы n -членов геометрической прогрессии): Откуда найдем первый член геометрической прогрессии: В нашем случае: В таблице 4 представлен план погашения кредита, когда выплаты изменяются в геометрической прогрессии.
Сумма 20 Процент 10% 1,05 Годы Остаток долга Величина платежа, Y Процентный платеж по кредиту, I Погашение долга, R 1 20 5,6195 2,0000 3,61950 2 16,380504 5,4385 1,6381 3,8005 3 12,580033 5,2485 1,2580 3,9905 4 8,589539 5,0490 0,8590 4,1900 5 4,39952 4,8395 0,4400 4,3995 26,1950 6,1950 20,0000 Таблица 4 План погашения кредита выплатами, изменяющимися в геометрической прогрессии
Если по условиям займа должник обязуется вернуть сумму долга в конце срока в виде разового платежа, то он должен предпринять меры для обеспечения этого. При значительной сумме долга возникает необходимость в создании погасительного фонда. Погасительный фонд создается из последовательных взносов должника (например, на специальный счет в банке), на которые начисляются проценты. Сумма взносов в фонд вместе с начисленными процентами, накопленная к концу срока в погасительном фонде, должна быть равна сумме долга. Взносы могут быть как постоянными, так и переменными. Если погасительный фонд создается для уплаты займа, условия которого предусматривают периодическую выплату процентов, то текущие расходы должника по займу состоят из двух элементов: платежа в погасительный фонд и выплаты процентов по займу.
При создании погасительного фонда фигурируют две ставки процентов – i и g. Первая определяет скорость роста суммы погасительного фонда, вторая – сумму выплачиваемых за заем процентов. Создание погасительного фонда выгодно должнику, если i >g, так как в этом случае должник на аккумулированные в погасительном фонде средства получает больший процент, чем сам выплачивается займ. При условии, что взносы в погасительный фонд и начисление процентов на него, а также выплата процентов по займу осуществляются один раз в конце года. Срочную уплату определяют по формуле: Y = I + R, где Y – срочная уплата, I — размер процентов, выплачиваемых кредитору, R — погасительный платеж. При постоянных погасительных платежах платежи образуют наращенную сумму, которая по величине равна долгу. Размер погасительного платежа рассчитывается по формуле: где С0 – общая сумма долга.
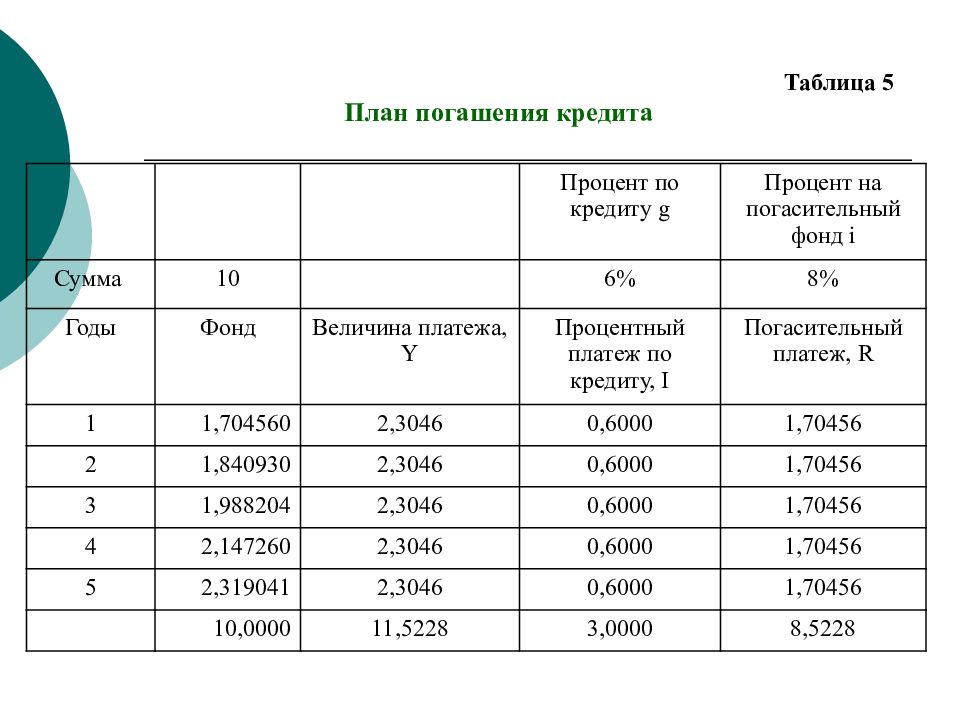
Пример Кредит в размере 10 млн. руб. выданный под 6% годовых должен быть погашен через 5 лет. Решено создать погасительный фонд. На погасительные платежи в банке начисляют 8% в год. Необходимо разработать план погашения кредита. Решение: Погасительный взнос равен: Срочная уплата составит:
Таблица 5 План погашения кредита Процент по кредиту g Процент на погасительный фонд i Сумма 10 6% 8% Годы Фонд Величина платежа, Y Процентный платеж по кредиту, I Погасительный платеж, R 1 1,704560 2,3046 0,6000 1,70456 2 1,840930 2,3046 0,6000 1,70456 3 1,988204 2,3046 0,6000 1,70456 4 2,147260 2,3046 0,6000 1,70456 5 2,319041 2,3046 0,6000 1,70456 10,0000 11,5228 3,0000 8,5228
Кредитные процентные ставки Погашение займа равными срочными годовыми выплатами Погашение кредита равными выплатами основного долга Выплаты изменяются в арифметической прогрессии Выплаты изменяются в геометрической прогрессии Погасительный фонд
