Первый слайд презентации: МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ
к.пс.н. Щеглова Э.А.
Слайд 2: РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Гусев А.Н. Дисперсионный анализ в экспериментальной психологии. – М., 2000. Ермолаев О. Ю. Математическая статистика для психологов: Учебник. – М.: МПСИ: Флинта, 2004. Константинов В.В. Экспериментальная психология. Курс для практического психолога. – СПб.: Питер, 2006. Кутейников А.Н. Математические методы в психологии. Учебное пособие. – СПб.: Речь, 2008. Митина О.В. Математические методы в психологии. – М.: Аспект Пресс, 2008. Митина О.В., Михайловская И.Б. Факторный анализ для психологов. – М., 2001. Наследов А.Д., Тарасов С.Г. Применение математических методов в психологии. – СПб, 2002. Наследов А.Д. SPSS 19: Профессиональный статистический анализ данных. – СПб.: Питер, 2011. Наследов Д.А. Наследов А.Д. Математические методы психологического исследования: анализ и интерпретация данных. – СПб.: Речь, 2008. Наследов Д.А. SPSS : Компьютерный анализ данных в психологии и социальных науках. – СПб.: Питер, 2005. Резник А.Д. Книга для тех, кто не любит статистику, но вынужден ею пользоваться. Непараметрическая статистика в примерах, упражнениях и рисунках. – СПб.: Речь, 2008. Рубцова Н.Е., Леньков С.Л. Статистические методы в психологии. – М.: УМК «Психология», 2005. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: Речь, 2010. Суходольский Г.В. Основы математической обработки в психологии. – Харьков. Гуманитарный центр, 2004.
Слайд 3: Психолог должен уметь:
организовать исследование так, чтобы его результаты были доступны обработке в соответствии с проблемами исследования; правильно выбрать метод обработки; содержательно интерпретировать результаты обработки.
Слайд 4: ОСНОВНЫЕ ПОНЯТИЯ
Гипотеза – это научно обоснованное предположение о свойствах и закономерностях изучаемого явления. Нулевая гипотеза Н о – это гипотеза об отсутствии значимых различий между какими-либо показателями или о случайности связи между ними. Альтернативная гипотеза Н 1 – это гипотеза о наличии значимых различий между исследуемыми показателями или о достоверности связи между ними.
Слайд 5: ОСНОВНЫЕ ПОНЯТИЯ
Направленные гипотезы : Н о : Х1 не превышает Х2. Н 1 : Х1 превышает Х2. Ненаправленные гипотезы : Н о : Х1 не отличается от Х2. Н 1 : Х1 отличается от Х2.
Слайд 6: ОСНОВНЫЕ ПОНЯТИЯ
Генеральная совокупность – это множество объектов, в отношении которого формулируется исследовательская гипотеза. Выборка – это ограниченная по численности группа объектов (испытуемых, респондентов), специально отбираемая из генеральной совокупности для изучения ее свойств.
Слайд 7: ОБЪЕМ ВЫБОРКИ ( n )
При разработке диагностической методики объем выборки должен быть от 200 до 1000 – 2500 человек. При сравнении 2-х выборок, их общая численность должна быть не менее 50 человек. При изучении взаимосвязи между какими-либо свойствами объем выборки должен быть не менее 30 – 35 человек. Чем больше изменчивость изучаемого свойства, тем больше должен быть объем выборки.
Слайд 8: ОСНОВНЫЕ ПОНЯТИЯ
Независимые выборки (несвязанные) характеризуются тем, что вероятность отбора любого испытуемого одной выборки не зависит от отбора любого из испытуемых другой выборки. Зависимые выборки (связанные) характеризуются тем, что каждому испытуемому одной выборки поставлен в соответствие по определенному критерию испытуемый из другой выборки.
Репрезентативность выборки Статистическая достоверность результатов исследования
Слайд 10: СТАТИСТИЧЕСКАЯ ДОСТОВЕРНОСТЬ
Статистическая достоверность (статистическая значимость, уровень статистической значимости, р -уровень) – это количественно выраженная вероятность того, что полученные результаты достоверны. р ≤0,05 – приемлемая граница статистической значимости.
Слайд 11: Соотношение показателей р-уровня и степени значимости результатов исследования
р-уровень Решение Возможный статистический вывод р 0,1 Принимается Н о «Статистически достоверные различия не обнаружены» 0,05 р 0,1 Сомнения в истинности Н о, неопределенность «Различия обнаружены на уровне статистической тенденции» р 0,05 Значимость, отклонение Н о «Обнаружены статистически достоверные (значимые) различия» р 0,01 Высокая значимость, отклонение Н о «Различия обнаружены на высоком уровне статистической значимости»
Слайд 12: СТАТИСТИЧЕСКИЕ КРИТЕРИИ
Статистический критерий – это решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой степенью надежности (вероятности). Статистические критерии обозначают и метод расчета определенного числа и само это число.
Слайд 13: СТАТИСТИЧЕСКИЕ КРИТЕРИИ
Параметрические критерии – это критерии построенные на основании параметров данной совокупности и представляют функции этих параметров. Они включают в расчетную формулу параметры распределения признака (среднее, дисперсию и др.).
Слайд 14: СТАТИСТИЧЕСКИЕ КРИТЕРИИ
Непараметрические критерии представляют собой функции, зависящие непосредственно от вариант данной совокупности с их частотами. Они основаны на оперировании частотами и рангами.
Слайд 15: ИЗМЕРИТЕЛЬНЫЕ ШКАЛЫ
НЕМЕТРИЧЕСКИЕ ШКАЛЫ : Номинативная шкала (номинальная, шкала наименований ); Порядковая шкала (ранговая шкала ). МЕТРИЧЕСКИЕ ШКАЛЫ: Интервальная шкала; Абсолютная шкала (шкала отношений ).
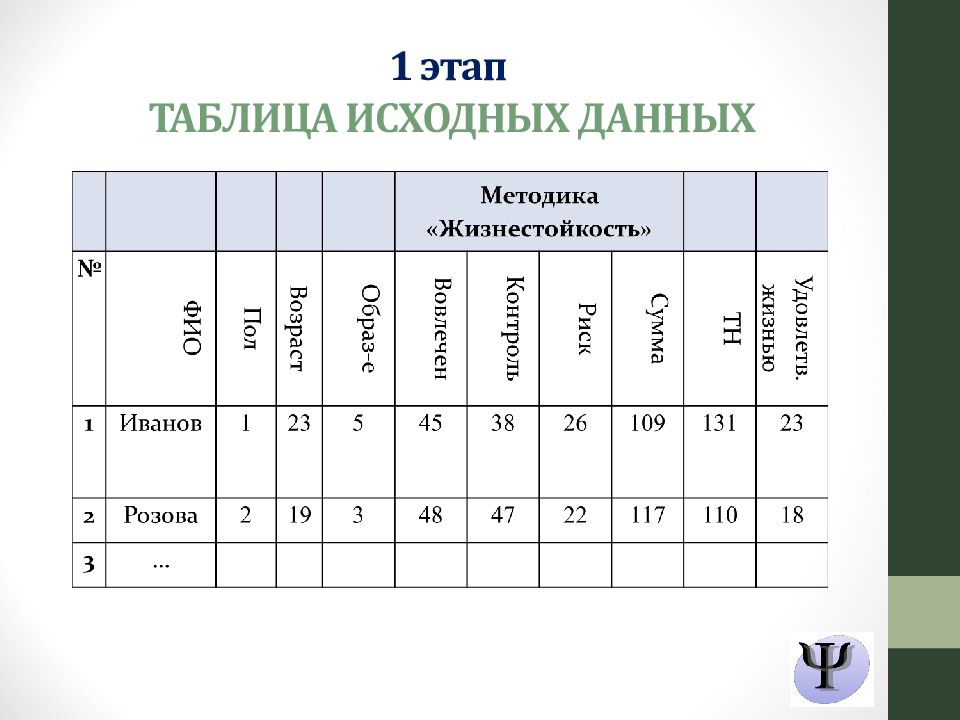
Слайд 16: ОСНОВНЫЕ ЭТАПЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ
Составить таблицу исходных данных. Провести первичный анализ данных (таблиц и графиков распределения частот, описательных статистик). Определить характер распределения признаков. Выбрать статистические методы обработки данных. Провести статистический анализ. Проинтерпретировать результаты, сформулировать выводы.
Слайд 18: 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
Таблицы распределения частот (показывают частоту встречаемости каждого значения признака) 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
Слайд 19: 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
Таблицы сопряженности (кросс-табуляции) - таблицы совместного распределения частот двух или более номинативных признаков, измеренных на одной группе объектов 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
Слайд 20: 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
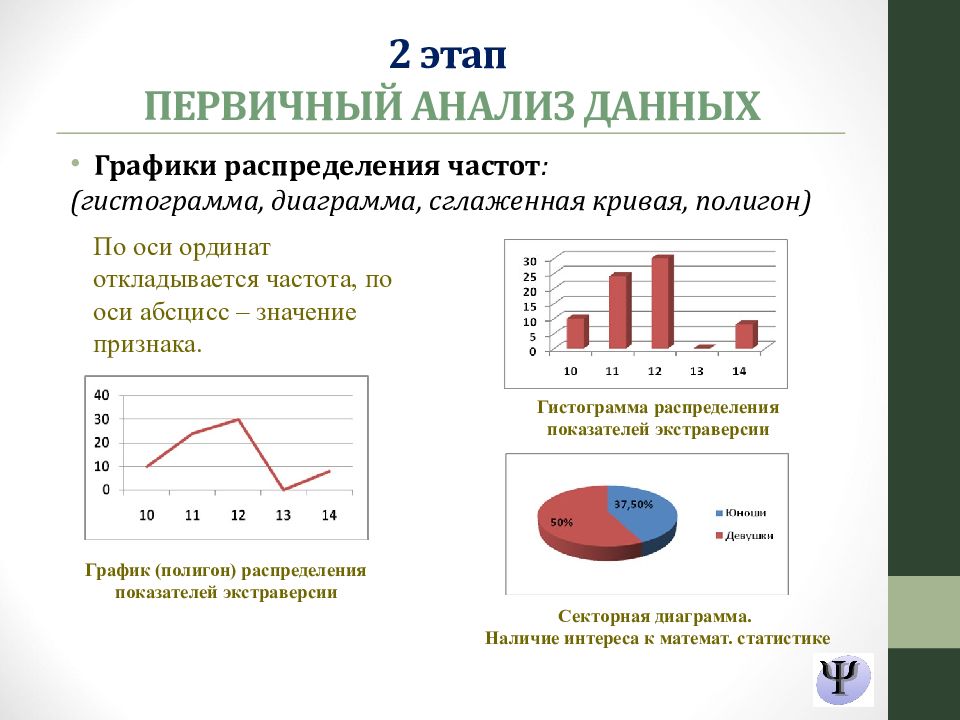
Графики распределения частот : (гистограмма, диаграмма, сглаженная кривая, полигон) По оси ординат откладывается частота, по оси абсцисс – значение признака. График (полигон) распределения показателей экстраверсии Гистограмма распределения показателей экстраверсии Секторная диаграмма. Наличие интереса к математ. статистике 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
Слайд 21: 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
ОПИСАТЕЛЬНЫЕ СТАТИСТИКИ Меры центральной тенденции: Среднее арифметическое (М) Медиана ( М е ) Мода (М о ) Меры изменчивости признака: Размах ( R ) Дисперсия ( D) Стандартное отклонение ( σ ) 2 этап ПЕРВИЧНЫЙ АНАЛИЗ ДАННЫХ
Слайд 22: СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
x i – сумма наблюдаемых значений признака; n – количество наблюдений (объем выборки).
Слайд 25: СТАТИСТИЧЕСКАЯ ОШИБКА СРЕДНЕГО АРИФМЕТИЧЕСКОГО
– стандартное отклонение; п – количество наблюдений (объем выборки).
Слайд 26: ПРЕДСТАВЛЕНИЕ ОПИСАТЕЛЬНЫХ СТАТИСТИК
повествовательное изложение результатов; графическое представление результатов; представление результатов в виде таблицы: № Психологический признак М± m σ min max 1 Показатель макиавеллизма 73,20±0,78 13,24 39 106 2 …
Слайд 27: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
ФОРМЫ РАСПРЕДЕЛЕНИЯ ПРИЗНАКА: Равномерное распределение. Симметричное распределение. Асимметричное левостороннее распределение. Асимметричное правостороннее распределение. Нормальное распределение (симметричное распределение). 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
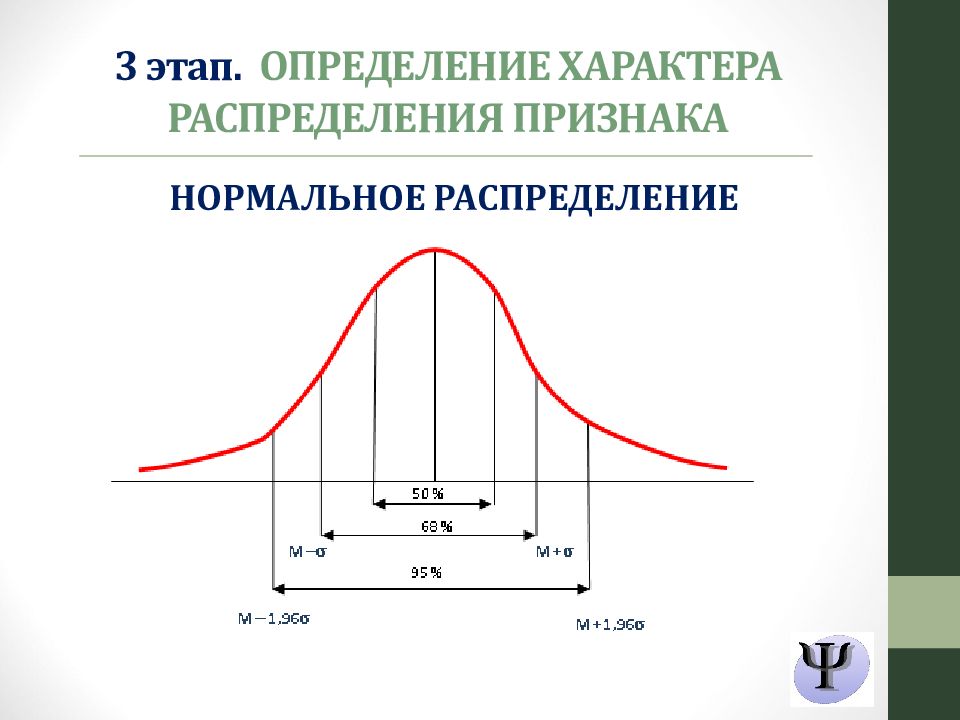
Слайд 28: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Слайд 29: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Метод оценки мер центральной тенденции. Визуальный (графический) метод. Метод оценки показателей асимметрии и эксцесса. Методы, основанные на критериях согласия распределений. 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Слайд 30: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Коэффициент асимметрии: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА Стандартная ошибка асимметрии:
Слайд 31: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА
Показатель эксцесса: 3 этап. ОПРЕДЕЛЕНИЕ ХАРАКТЕРА РАСПРЕДЕЛЕНИЯ ПРИЗНАКА Стандартная ошибка эксцесса:
Слайд 32: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
КРИТЕРИИ: Цель и задачи исследования Особенности выборок Вид эмпирических данных Характер распределения признаков
Слайд 33: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 1: Сопоставление двух признаков, измеренных на одной и той же выборке испытуемых, установление степени согласованности их распределений. МЕТОД: Анализ взаимосвязи признаков Корреляционный анализ. Регрессионный анализ. 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 34: ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗИ ПРИЗНАКОВ
Корреляция – согласованность изменения признаков. Коэффициент корреляции r ( -1 ≤ r ≤ 1). r =0 – отсутствие взаимосвязи между признаками; r >0 – прямая (положительная) взаимосвязь; r <0 – обратная (отрицательная) взаимосвязь
Слайд 35: КОЭФФИЦИЕНТ ЛИНЕЙНОЙ КОРРЕЛЯЦИИ ПИРСОНА
х, y – значения исследуемых признаков; М х, М у – средние значения исследуемых признаков; σ х, σ у – стандартные отклонения; n – количество наблюдений.
Слайд 36: КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ СПИРМЕНА
d – разность рангов; n – количество наблюдений.
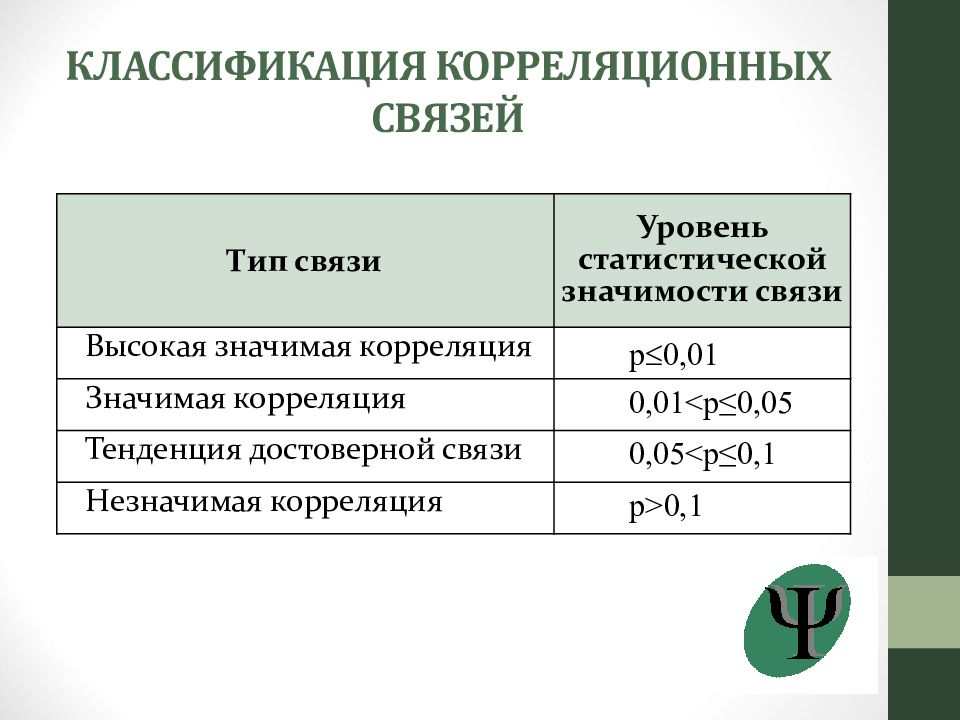
Слайд 37: КЛАССИФИКАЦИЯ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ
Тип связи Уровень статистической значимости связи Высокая значимая корреляция р 0,01 Значимая корреляция 0,01<р≤0,05 Тенденция достоверной связи 0,05<р≤0,1 Незначимая корреляция р>0,1
Слайд 38: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 2: Сравнение разных групп испытуемых по какому-либо признаку, выявление различий между ними по данному признаку. МЕТОД : Статистические критерии различий для 2-х выборок : t -критерий Стьюдента, U-критерий Манна-Уитни, *-критерий (угловое преобразование Фишера); для 3-х и более выборок : однофакторный дисперсионный анализ, Н-критерий Крускала -Уоллеса. 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 39: ИССЛЕДОВАНИЕ РАЗЛИЧИЙ В УРОВНЕ ПРИЗНАКА
t -критерий Стьюдента (для 2-х независимых выборок): Если t эмп ≥ t кр (р≤0,05) Н 0 отвергают и принимают Н 1
Слайд 40: ИССЛЕДОВАНИЕ РАЗЛИЧИЙ В УРОВНЕ ПРИЗНАКА
U -критерий Манна-Уитни (для 2-х независимых выборок): n 1, n 2 - объемы выборок, R 1, R 2 - суммы рангов по выборкам, R max - наибольшая из двух ранговых сумм, n x — объем выборки, имеющей наибольшую сумму рангов.
Слайд 41: ИССЛЕДОВАНИЕ РАЗЛИЧИЙ В УРОВНЕ ПРИЗНАКА
Н-критерий Крускала-Уоллиса (для 3-х и более независимых выборок): R – это суммы рангов по группам; k - количество групп; n k – объемы групп n – объем объединенной выборки (общая численность наблюдений)
Слайд 42: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 3: Сравнение каких-либо переменных до экспериментальных воздействий и после них, определение эффективности этих воздействий. МЕТОД: Статистические критерии сдвига для 2-х выборок : t-критерий Стьюдента, T-критерий Уилкоксона, G-критерий знаков; для 3-х и более выборок : критерий Фридмана 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 43: ИССЛЕДОВАНИЕ ДОСТОВЕРНОСТИ СДВИГА
t -критерий Стьюдента (для 2-х связанных выборок): M d = d i = ( y i – x i ) ; M d – среднее арифметическое разностей индивидуальных значений; d – стандартное отклонение значений разностей. Число степеней свободы: df = n – 1
Слайд 44: ИССЛЕДОВАНИЕ ДОСТОВЕРНОСТИ СДВИГА
Т-критерий Вилкоксона (для 2-х связанных выборок): R r – сумма нетипичных (более редких) рангов.
Слайд 45: ИССЛЕДОВАНИЕ ДОСТОВЕРНОСТИ СДВИГА
Критерий Фридмана (для 3-х и более связанных выборок): n – число строк в таблице (размер выборки) k – число столбцов в таблице (количество измерений); R i, – сумма рангов, соответственно, для первого, второго и третьего ( i -того) столбцов.
Слайд 46: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 3: Сопоставление эмпирического распределения признака с теоретическим законом распределения, или два эмпирических распределения между собой чтобы доказать не случайность выбора альтернатив или различий в форме распределений. МЕТОД: Статистические критерии согласия распределений критерий Колмагорова -Смирнова, критерий 2 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 47: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 5: Изучение результатов влияния и силы влияния более чем одной независимой переменной на одну зависимую переменную. МЕТОД: Многофакторный дисперсионный анализ. Множественный регрессионный анализ. 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 48: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 6 : Выявление латентных переменных (факторов), отвечающих за наличие линейных статистических связей между наблюдаемыми переменными, снижение размерности, создание факторной структуры исходя из множества наблюдаемых переменных. МЕТОД: Факторный анализ. 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 49: 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
ЗАДАЧА 7 : Группировка объектов, характеризующихся общими свойствами, с целью разработки типологии или классификации. МЕТОД: Кластерный анализ. 4 этап ВЫБОР СТАТИСТИЧЕСКОГО МЕТОДА
Слайд 51: ДИСПЕРСИОННЫЙ АНАЛИЗ
Дисперсионный анализ (ANOVA) – статистический метод оценки изменчивости признака под влиянием каких-либо контролируемых переменных факторов.
Слайд 52: ДИСПЕРСИОННЫЙ АНАЛИЗ
D oбщ. = D факт + D ост. D oбщ. – общая дисперсия наблюдаемых значений (вариант), характеризуется разбросом вариант от общего среднего. Измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. ДИСПЕРСИОННЫЙ АНАЛИЗ
Слайд 53: ДИСПЕРСИОННЫЙ АНАЛИЗ
D факт – факторная или межгрупповая дисперсия, характеризуется различием средних в каждой группе и зависит от влияния исследуемого фактора, по которому дифференцируется каждая группа. D ост. – остаточная или внутригрупповая дисперсия, которая характеризует рассеяние вариант внутри групп. Отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неуточненных факторов и не зависящую от признака – фактора, положенного в основание группировки. ДИСПЕРСИОННЫЙ АНАЛИЗ
Слайд 54: ДИСПЕРСИОННЫЙ АНАЛИЗ
Градации фактора – уровни (степень) выраженности признака. Дисперсионный комплекс – экспериментальные данные, представленные по градациям фактора. Ячейки комплекса – данные, относящиеся к отдельным градациям. ДИСПЕРСИОННЫЙ АНАЛИЗ
Слайд 55: ЭТАПЫ ДИСПЕРСИОННОГО АНАЛИЗА
Построение дисперсионного комплекса. Вычисление средних квадратов отклонений. Вычисление дисперсии. Сравнение факторной и остаточной дисперсий. Оценка результатов с помощью теоретических значений распределения Фишера. ЭТАПЫ ДИСПЕРСИОННОГО АНАЛИЗА
Слайд 56: ВИДЫ ДИСПЕРСИОННОГО АНАЛИЗА
Однофакторный дисперсионный анализ. Двухфакторный дисперсионный анализ. Многофакторный дисперсионный анализ. ВИДЫ ДИСПЕРСИОННОГО АНАЛИЗА
Слайд 57: ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Однофакторный дисперсионный анализ для независимых выборок. Однофакторный дисперсионный анализ с повторными измерениями (для связанных выборок) ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Слайд 58: ОГРАНИЧЕНИЯ ОДНОФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА
Зависимая переменная (результативный признак) должна быть представлена в метрической шкале. Независимые переменные (факторы) должны иметь нечисловую природу, т.е. должны быть измерены в номинативной шкале. Должно быть не менее трех градаций фактора и не менее двух испытуемых в каждой градации. Должно соблюдаться правило равенства дисперсии в каждой ячейке дисперсионного комплекса. Результативный признак должен быть нормально распределен в исследуемой выборке. ОГРАНИЧЕНИЯ ОДНОФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА
Слайд 59: ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Двухфакторный дисперсионный анализ для независимых выборок. Двухфакторный дисперсионный анализ для связанных выборок.
Слайд 60: ОГРАНИЧЕНИЯ ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА
Зависимая переменная (результативный признак) должна быть представлена в метрической шкале. Независимые переменные (факторы) должны иметь нечисловую природу, т.е. должны быть измерены в номинативной шкале. У каждого фактора должно быть не менее двух градаций. В каждой ячейке комплекса должно быть не менее двух наблюдаемых значений для выявления взаимодействия градаций. Количества значений во всех ячейках комплекса должны быть равны для обеспечения равенства дисперсий в ячейках комплекса. ОГРАНИЧЕНИЯ ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА
Слайд 61: ОГРАНИЧЕНИЯ ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА
Комплекс должен представлять собой симметричную систему: каждой градации фактора А должно соответствовать одинаковое количество градаций фактора В. Результативный признак должен быть нормально распределен в исследуемой выборке, иначе значимые различия будет выявить гораздо труднее и применение метода будет не вполне корректным. Факторы должны быть независимыми (не должны коррелировать между собой). В случае связанных выборок для достижения равномерности комплекса все испытуемые должны пройти все сочетания градаций двух факторов. ОГРАНИЧЕНИЯ ДВУХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА
Слайд 62: МНОГОМЕРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ ( MANOVA )
Ограничения многомерного дисперсионного анализа: Должно быть не менее двух зависимых переменных и, как минимум одна независимая переменная. Не должно быть линейной функциональной связи между зависимыми переменными (они не должны значимо коррелировать между собой). МНОГОМЕРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ ( MANOVA )
Слайд 63: МНОГОМЕРНЫЕ МЕТОДЫ
Многомерные методы позволяют обоснованно выбрать среди множества вероятностных статистических моделей такую, которая наилучшим образом соответствует исходным статистическим данным, характеризующим реальное поведение исследуемой совокупности объектов, оценить надежность и точность выводов, сделанных на основании большого статистического материала.
Слайд 64: МНОГОМЕРНЫЕ МЕТОДЫ
Классификация методов по назначению : Методы предсказания (экстраполяции): множественный регрессионный и дискриминантный анализ. Методы классификации : варианты кластерного анализа и дискриминантный анализ. Структурные методы : факторный анализ и многомерное шкалирование. МНОГОМЕРНЫЕ МЕТОДЫ
Слайд 65: МНОГОМЕРНЫЕ МЕТОДЫ
Классификация методов по исходным предположениям о структуре данных : Методы, основанные на корреляционной модели, исходящие из предположения о согласованной изменчивости признаков, измеренных у множества объектов (факторный анализ, множественный регрессионный анализ, отчасти – дискриминантный анализ). Методы, основанные на дистантной модели, исходящие из предположения о том, что различия между объектами можно описать как расстояние между ними (кластерный анализ, многомерное шкалирование, частично – дискриминантный анализ). МНОГОМЕРНЫЕ МЕТОДЫ
Слайд 66: МНОГОМЕРНЫЕ МЕТОДЫ
Классификация методов по виду исходных данных : Методы, использующие в качестве исходных данных только признаки, измеренные у группы объектов (множественный регрессионный анализ, дискриминантный анализ и факторный анализ). Методы, исходными данными для которых могут быть попарные сходства (различия) между объектами (кластерный анализ и многомерное шкалирование ). МНОГОМЕРНЫЕ МЕТОДЫ
Слайд 67: РЕГРЕССИОННЫЙ АНАЛИЗ
Ориентирован на планирование и прогнозирование, позволяет по имеющимся данным предсказывать новые результаты. Цель регрессионного анализа - статистически адекватно описать зависимость, прогнозируемых («выходных» ) переменных от ряда других независимых переменных. Независимые переменные – предикторы, регрессоры, факторы. Зависимые переменные – отклики.
Слайд 68
РЕГРЕССИЯ ЛИНЕЙНАЯ (зависимость между откликами и предикторами задается линейным уравнением) НЕЛИНЕЙНАЯ (зависимость между откликами и предикторами задается нелинейным уравнением) ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ (зависимость отклика от одного предиктора) МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ (зависимость отклика от двух и более предикторов)
Слайд 69: МОДЕЛЬ ПРОСТОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Y – предсказанное значение отклика, X - значение предиктора, b 0 - константа регрессии для отклика Y, b 1 - коэффициент регрессии для отклика Y, e – остаток для отклика Y.
Слайд 70: МОДЕЛЬ МНОЖЕСТВЕННОЙ ЛИНЕЙНОЙ РЕГРЕССИИ
Y – предсказанное значение отклика, X i - значения предикторов, b 0 - константа регрессии для отклика Y, b k - коэффициенты регрессии для отклика Y, e – остаток для отклика Y.
Слайд 71: ТРЕБОВАНИЯ К ПРИМЕНЕНИЮ РЕГРЕССИОННОГО АНАЛИЗА
Исследование должно быть продумано по форме и исполнению. Объем выборки N > 50. Использование только метрических данных. Соответствие вероятностных распределений предикторов, отклика и остатков нормальному закону. Некоррелированность предикторов между собой.
Слайд 72: МЕТОДЫ РЕГРЕССИОННОГО АНАЛИЗА
Стандартный метод учитывает при получении коэффициентов регрессии все изначально заданные предикторы. Пошаговый метод ( Stepwise ) ориентирован на получение наилучшего (оптимального) подмножества предикторов, обеспечивающего наиболее высокое качество регрессии. МЕТОДЫ РЕГРЕССИОННОГО АНАЛИЗА
Слайд 73: ПРЯМОЙ ПОШАГОВЫЙ МЕТОД
В уравнение регрессии поочередно «включается» каждая переменная, начиная с предиктора, наиболее тесно коррелирующего с откликом. Процесс продолжается до тех пор, пока происходит прирост коэффициента множественной корреляции. В результате удается получить максимально возможное количество предикторов, обеспечивающих наиболее высокий коэффициент множественной корреляции.
Слайд 74: ОБРАТНЫЙ ПОШАГОВЫЙ МЕТОД
Процесс начинается с рассмотрения всех предикторов, которые затем поочередно исключаются из уравнения регрессии. В результате получают минимальное количество предикторов, обеспечивающих статистически значимый коэффициент множественной корреляции.
Слайд 75: РЕГРЕССИОННЫЙ АНАЛИЗ
R – коэффициент множественной корреляции, коэффициент характеризующий связь между значениями зависимой и независимой переменных. р – уровень статистической значимости, вероятность случайности полученного результата. R 2 – коэффициент детерминации, характеризующий долю дисперсии зависимой переменной, обусловленную воздействием со стороны независимой переменной (независимых переменных). В -величины – константа и коэффициенты уравнения регрессии ( нестандартизированные ). β – стандартные коэффициенты регрессии, представляют собой коэффициенты В для независимых переменных, представленных в z -шкале. РЕГРЕССИОННЫЙ АНАЛИЗ
Слайд 76: ФАКТОРНЫЙ АНАЛИЗ
Факторный анализ – метод, позволяющий свести большое количество исходных переменных к значительно меньшему числу факторов, каждый из которых объединяет исходные переменные, имеющие сходный смысл. Факторный анализ дает возможность количественно определить то, что непосредственно измерить невозможно, исходя из нескольких доступных измерению переменных.
Слайд 77: ВИДЫ ФАКТОРНОГО АНАЛИЗА
Эксплораторный факторный анализ (разведочный) – создание оптимальной с математической точки зрения группировки переменных в факторы. Конфирматорный факторный анализ (подтверждающий) – предназначен для проверки гипотез о числе факторов и их нагрузках.
Слайд 78: БАЗОВЫЕ ПОНЯТИЯ
Факторизация – процедура извлечения факторов с помощью корреляционной матрицы исходных данных. Факторная структура – набор выделенных в результате факторного анализа общих факторов, которые заменяют собой исходные признаки. Фактор – латентная (скрытая) переменная.
Слайд 79: БАЗОВЫЕ ПОНЯТИЯ
Общие факторы - выделяемые при факторном анализе латентные факторы, в той или иной мере воздействующие на все рассматриваемые признаки. Специфические факторы (невязки, остаточные факторы) - выделяемые при факторном анализе латентные факторы, воздействующие на какой-либо один определенный признак.
Слайд 80: БАЗОВЫЕ ПОНЯТИЯ
Факторная нагрузка – коэффициент взаимосвязи между некоторой переменной и общим фактором, выражающий меру влияния фактора на признак. Факторная матрица – матрица, составленная из координат общих факторов. Факторный вес – коэффициент факторной матрицы, мера проявления фактора у отдельного объекта. БАЗОВЫЕ ПОНЯТИЯ
Слайд 81: БАЗОВЫЕ ПОНЯТИЯ
Объясненная дисперсия – часть общей дисперсии, объясняемая с помощью выделенных факторов. Собственные значения – собственные значения матрицы, которые находятся для матрицы корреляций между признаками, построенной по нормированной матрице «объект - признак ». БАЗОВЫЕ ПОНЯТИЯ
Слайд 82: ПРОЦЕДУРА ФАКТОРНОГО АНАЛИЗА
Подготовка исходной матрицы данных. Вычисление корреляционной матрицы для всех переменных, участвующих в анализе. Факторизация (извлечение факторов). Вращение факторов для создания упрощенной структуры. Оценка факторных значений и интерпретация факторов.
Слайд 83: МЕТОДЫ ФАКТОРИЗАЦИИ
Метод главных компонент Метод главных факторов Метод максимального правдоподобия факторов Каноническая факторизация Рао Факторизация образов Альфа-факторизация Метод наименьших квадратов
Слайд 84: ХОРОШАЯ ФАКТОРНАЯ МОДЕЛЬ
Если число найденных главных компонент (факторов) меньше, чем количество исходных переменных в 2 и более раза. Если объясняемая этими факторами дисперсия не менее 70%, а следующая компонента дает вклад в суммарную дисперсию не более 5 %. Если выделенная факторная структура с содержательной точки зрения является логичной.
Слайд 85: ВЫБОР ФАКТОРОВ
При выборе значимых факторов следует руководствоваться: целью и задачами исследования, формальными критериями (критерий Кайзера, критерий «каменистой осыпи» и др.).
Слайд 86: ВРАЩЕНИЕ ФАКТОРОВ
Вращение факторов – математическая процедура, позволяющая прояснить содержательный смысл выделенных факторов. ВИДЫ ВРАЩЕНИЯ: Варимакс Прямой облимин Квартимакс Эквимакс Промакс
Слайд 87: ОЦЕНКА ФАКТОРНЫХ НАГРУЗОК
Нагрузки ≥ 0,71 (фактор объясняет 50% дисперсии ) — превосходные нагрузки. Нагрузки ≥ 0,63 (фактор объясняет 40 % дисперсии) — очень хорошие нагрузки. Нагрузки ≥ 0,55 (фактор объясняет 30% дисперсии) — хорошие нагрузки. Нагрузки ≥ 0,45 (фактор объясняет 20% дисперсии) — удовлетворительные нагрузки. Нагрузки = 0,32 (фактор объясняет 10% дисперсии) — слабые нагрузки.
Слайд 88: ОЦЕНКА ФАКТОРНЫХ ВЕСОВ
Положительные факторные веса - степень проявления фактора у объекта «выше средней». Факторные веса близкие к нулю – средняя степень проявления фактора у объекта. Отрицательные факторные веса – степень проявления фактора у объекта «ниже средней». ОЦЕНКА ФАКТОРНЫХ ВЕСОВ
Слайд 89: УСЛОВИЯ ПРИМЕНЕНИЯ ФАКТОРНОГО АНАЛИЗА
Считается, что истинными причинами изучаемого явления являются не непосредственно наблюдаемые и доступные измерению признаки, а скрытые (латентные) факторы, количество которых, как правило, неизвестно исследователю. Исходные переменные должны быть количественными. Достаточный объем выборки ( n не менее 150 чел.) Число наблюдений должно быть в два раза больше числа переменных.
Слайд 90: УСЛОВИЯ ПРИМЕНЕНИЯ ФАКТОРНОГО АНАЛИЗА
Выборка должна быть однородна. Предполагается нормальность распределения исходных переменных. Исходные переменные должны коррелировать между собой. В большинстве разновидностей факторного анализа постулируется ортогональность и независимость выявляемых факторов (на практике выполняется не всегда). УСЛОВИЯ ПРИМЕНЕНИЯ ФАКТОРНОГО АНАЛИЗА
Слайд 91: ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ФАКТОРНОГО АНАЛИЗА
В отчете необходимо указать : размерность первичной матрицы; метод факторизации и вращения; количество выделенных факторов и критерий их выделения; вклад каждого фактора в общую дисперсию и привести матрицу факторных нагрузок.
Слайд 92: КЛАСТЕРНЫЙ АНАЛИЗ
Кластерный анализ – это ряд статистических методов, используемых для группировки объектов (наблюдений или переменных) в классы (кластеры) на основе сходства их характерных признаков. Это многомерный статистический метод, предназначенный для решения задач классификации, позволяющий описать структуру совокупности объектов и отношений между ними.
Слайд 93: КЛАСТЕРНЫЙ АНАЛИЗ
Кластер – это группа элементов, характеризуемых общим свойством. Элементы, объединенные в один кластер, являются более похожими друг на друга, более близкими по каким-либо характеристикам по сравнению с элементами, образующими другие кластеры. КЛАСТЕРНЫЙ АНАЛИЗ
Слайд 94: МЕТОДЫ КЛАСТЕРНОГО АНАЛИЗА
Иерархические методы – первоначально все объекты рассматриваются как отдельные, кластеры. Выстраивается «дерево» кластеров путем объединения (или разъединения) первоначально существовавших кластеров. Итеративные методы – разбиение на кластеры получают из некоторого начального разбиения способом последовательных итераций. Число конечных кластеров исследователь задает самостоятельно. МЕТОДЫ КЛАСТЕРНОГО АНАЛИЗА
Слайд 95: МЕТОДЫ КЛАСТЕРНОГО АНАЛИЗА
Агломеративные методы – процедура кластеризации начинается с множества одноэлементных кластеров, соответствующих отдельным объектам, а заканчивается получением одного глобального общего кластера. Дивизивные методы – множество объектов первоначально представляют один кластер, который затем разделяется на некоторое количество кластеров при определенном удовлетворяющем исследователя качестве разделения. МЕТОДЫ КЛАСТЕРНОГО АНАЛИЗА
Слайд 96: ОСНОВНЫЕ ЭТАПЫ КЛАСТЕРНОГО АНАЛИЗА
Подготовка матрицы «объект-признак». Выбор направления кластеризации. Выбор стратегии (метода) кластеризации – основного принципа разделения выборки на кластеры. Выбор мер сходства или различия между кластерами (способа определения межкластерных расстояний). Формирование кластеров. Проверка результатов кластеризации. Психологическая интерпретация полученных результатов кластеризации.
Слайд 97: МЕТОДЫ ИЕРАРХИЧЕСКОЙ КЛАСТЕРИЗАЦИИ
Межгрупповые связи Внутригрупповые связи Ближайший сосед Дальний сосед Центроидная кластеризация Медианная кластеризация Метод Варда.
Слайд 98: МЕРЫ СХОДСТВА (РАЗЛИЧИЯ) МЕЖДУ КЛАСТЕРАМИ
Квадрат расстояния Евклида Косинус Корреляция Пирсона Расстояние Чебышева Блок Расстояние Минковского Настроенная
Слайд 100: ПРОВЕРКА РЕЗУЛЬТАТОВ КЛАСТЕРИЗАЦИИ
Необходимо проверить: не является ли полученное разбиение на кластеры случайным; является ли разбиение надежным и стабильным на подвыборках данных; существует ли взаимосвязь между результатами кластеризации и переменными, которые не участвовали в процессе кластеризации; можно ли логически интерпретировать полученные результаты кластеризации.
Слайд 101: ПРОЦЕДУРЫ ПРОВЕРКИ КАЧЕСТВА КЛАСТЕРИЗАЦИИ
анализ результатов кластеризации, полученных на определенных выборках набора данных; проведение кластеризации при изменении порядка наблюдений в наборе данных; проведение кластеризации при удалении некоторых наблюдений; проведение кластеризации на небольших выборках; использование нескольких методов и сравнение полученных результатов. ПРОЦЕДУРЫ ПРОВЕРКИ КАЧЕСТВА КЛАСТЕРИЗАЦИИ
Слайд 102: УСЛОВИЯ ПРИМЕНЕНИЯ КЛАСТЕРНОГО АНАЛИЗА
Исследуемые психологические признаки должны быть количественными. Распределение признаков должно быть близко к нормальному. Показатели не должны коррелировать между собой. Показатели должны быть устойчивыми, т.е. на их значения не должны оказывать влияние случайные факторы. Выборка должна быть однородна, не содержать «выбросов».
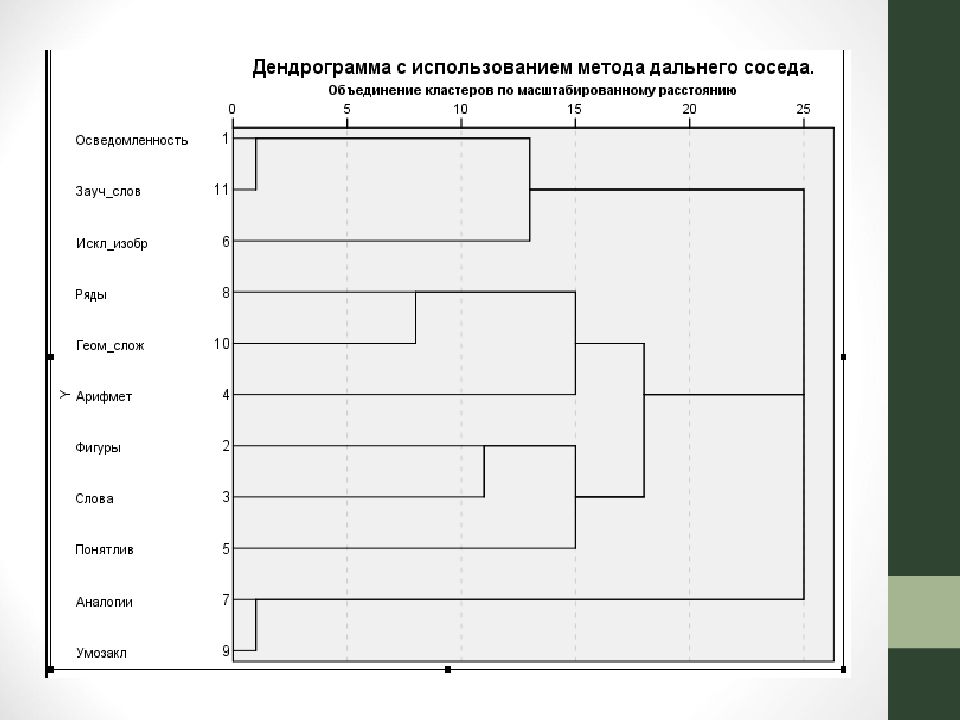
Последний слайд презентации: МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ: ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ КЛАСТЕРНОГО АНАЛИЗА
В отчете необходимо указать : какие данные подвергались кластеризации, направление кластеризации; метод кластеризации; стратегию кластеризации и способ определения межкластерного расстояния; результаты в табличном и графическом виде (таблицу шагов агломерации и дерево кластеризации); количество выделенных кластеров и их состав. ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ КЛАСТЕРНОГО АНАЛИЗА