Первый слайд презентации: Математика — это ключ и дверь ко всем наукам.“ Галилео Галилей - итальянский физик, механик, астроном, философ и математик XVII в. 1564–1642
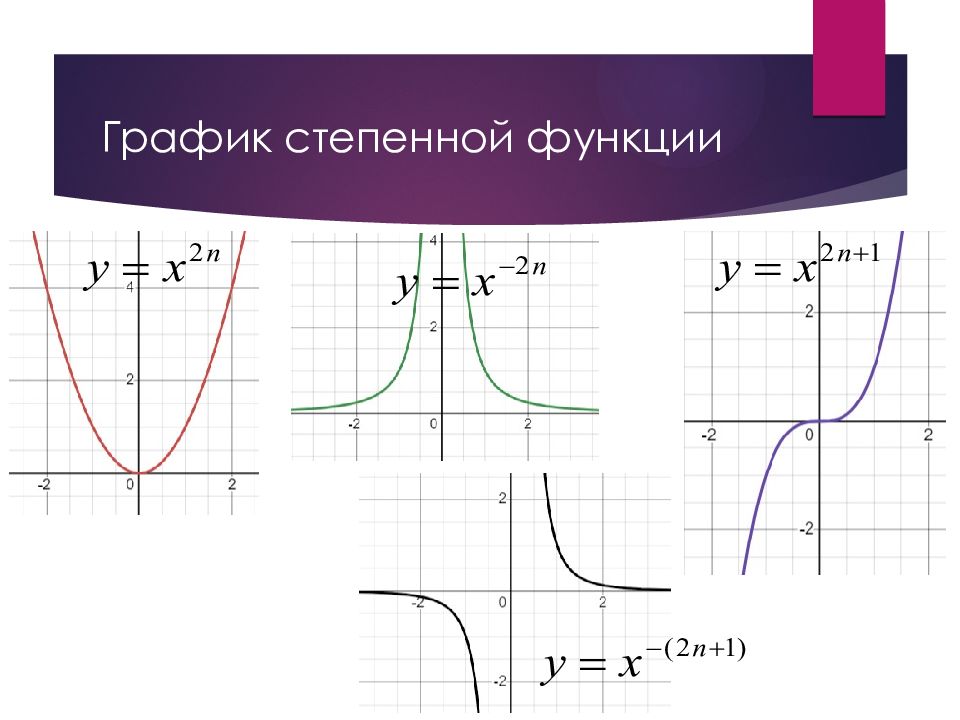
Слайд 4: Степенная функция
x – аргумент (основание степени) n – показатель степени. Отметим свойства общие для степенных функций: 1 ) при n >0 x >0 функция возрастающая 2) при n <0 x >0 функция убывающая
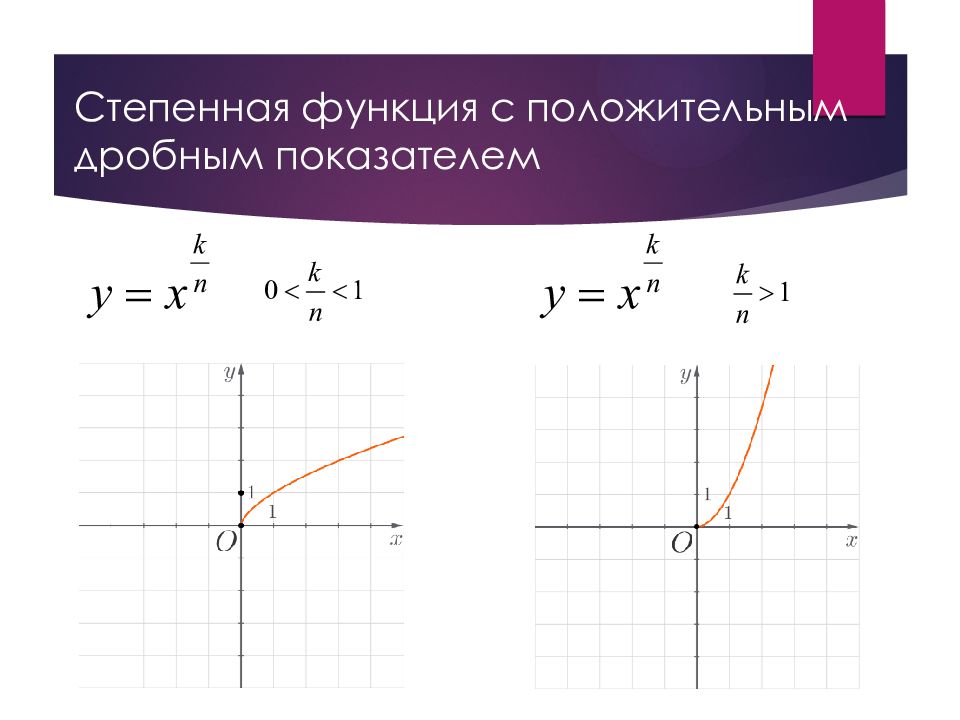
Слайд 6: Степенная функция с положительным дробным показателем
x – аргумент (основание степени) n >1, k ( натуральные числа) – показатель степени. Рассмотрим произвольные числа и из области определения, такие что <. Тогда, используя свойства числовых неравенств, получаем: а следовательно, функция возрастает на всей области определения.
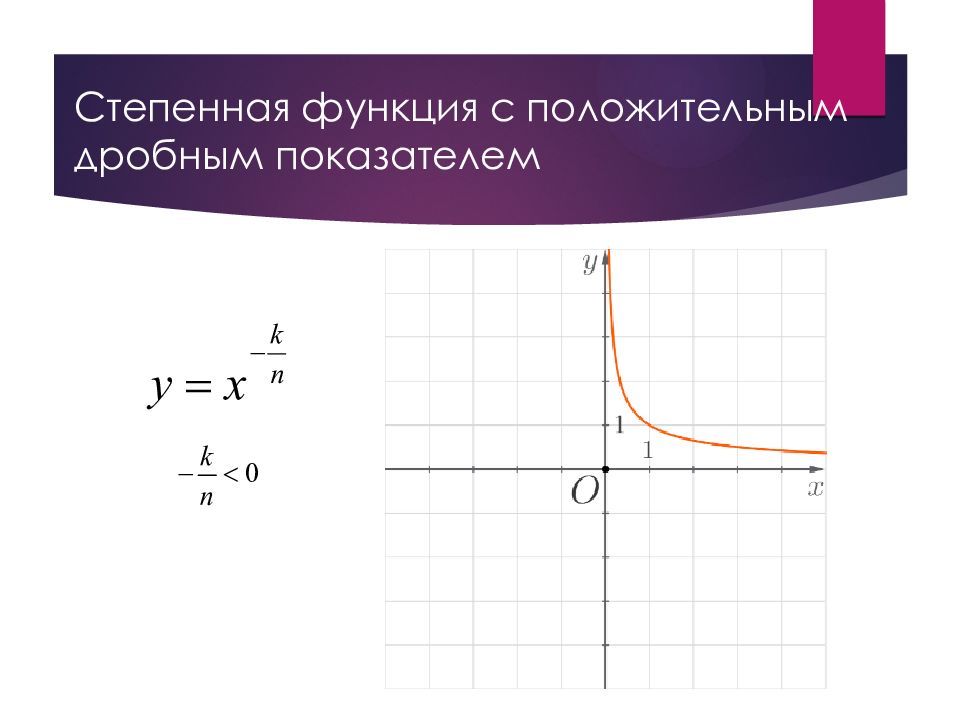
Слайд 8: Степенная функция с отрицательным дробным показателем
x – аргумент (основание степени) n >1, k ( натуральные числа) – показатель степени. Рассмотрим произвольные числа и из области определения, такие что <. Тогда, используя свойства числовых неравенств, получаем: а следовательно, функция убывает на всей области определения.
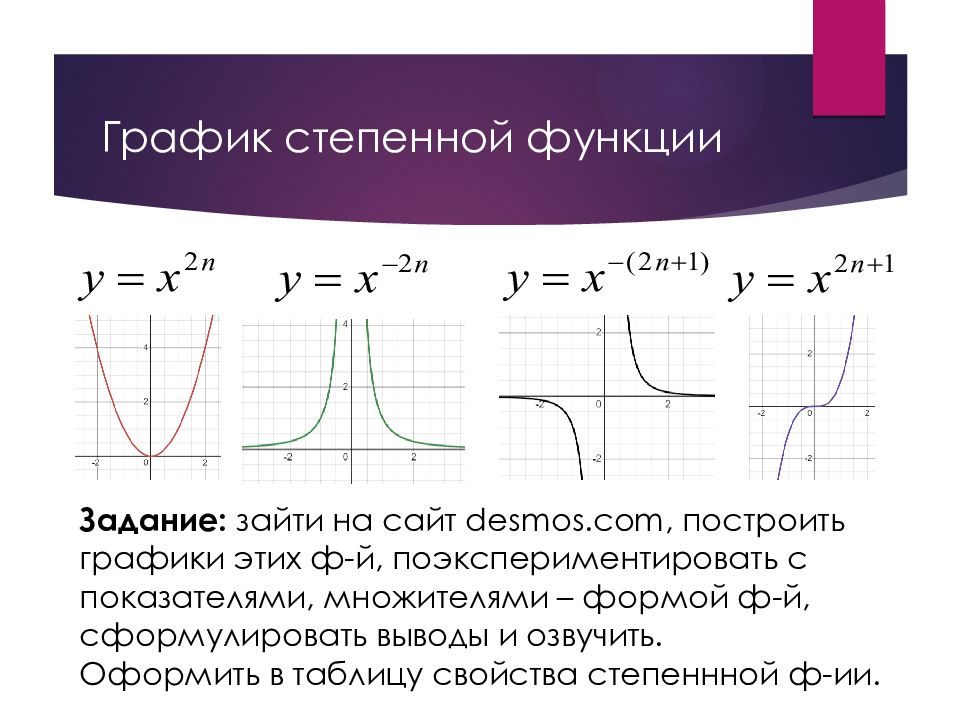
Слайд 10: График степенной функции
Задание: зайти на сайт desmos. com, построить графики этих ф-й, поэкспериментировать с показателями, множителями – формой ф-й, сформулировать выводы и озвучить. Оформить в таблицу свойства степеннной ф- ии.
Слайд 11
(-∞ ;+∞) ; (-∞ ; 0)U(0 ;+ ∞ ) [ 0;+ ∞ ); (0;+ ∞ ) Чётная, симметрия относительно оси Y Убывает (-∞ ; 0 ) и Возрастает ( 0 ;+∞ ); Возрастает (-∞ ; 0) и Убывает ( 0 ;+∞) Снизу Свойства D(f) E(f) Чётность / нечётность Монотонность Ограниченность (-∞ ;+∞); (-∞ ; 0)U(0 ;+∞ ) (-∞ ;+∞); (-∞ ; 0)U(0 ;+∞ ) Нечётная, симметрия относительно начала координат Возрастает (-∞ ;+∞ ); Убывает (-∞ ; 0)U(0 ;+∞) Не ограничена
Слайд 12
- ; - 0 ; - Непрерывна; Точка разрыва х=0 Выпукла вниз (-∞ ;+∞ ); Выпукла вниз (-∞ ; 0)U(0 ;+∞) Симметрия относительно у=х Свойства у наибольшее у наименьшее Непрерывность Выпуклость / вогнутость Обратная ф-я - ; - - ; - Непрерывна; Точка разрыва х=0 Выпукла вверх (-∞ ; 0 ] и Выпукла вниз [ 0 ;+∞ ) Симметрия относительно у=х