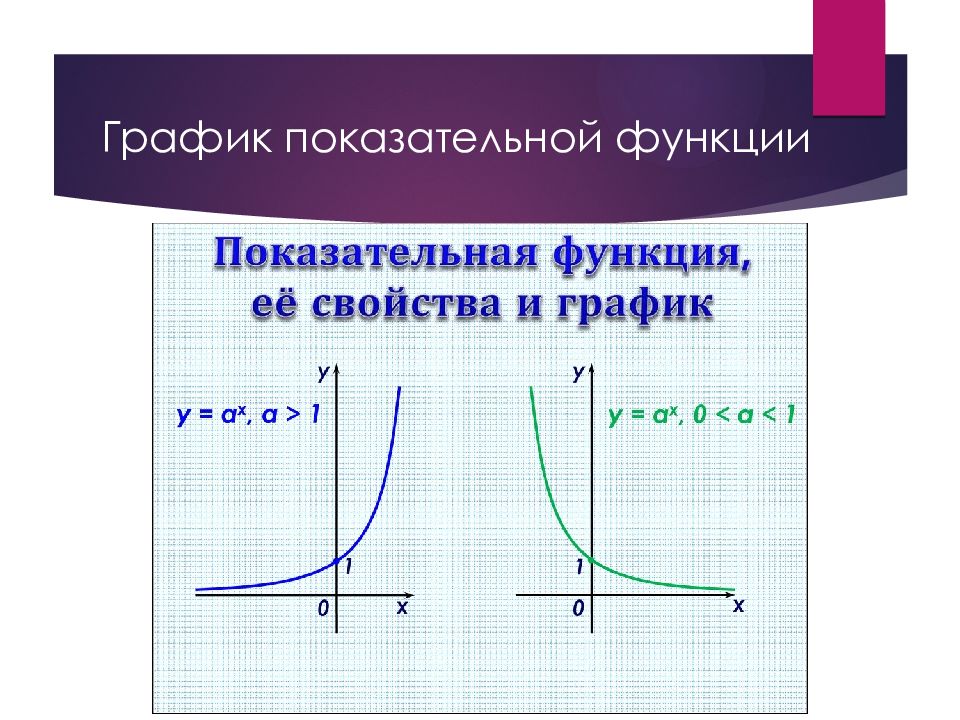
Слайд 4: Показательная функция
a – основание степени x – ( аргумент) показатель степени. a > 0, a ≠ 1, у > 0
Слайд 5: Показательная функция
Х -2 -1 0 1 2 3 У 1 2 4 8 Х -2 -1 0 1 2 3 У 1 2 4 8 Х -2 -1 0 1 2 3 У 4 2 1 Х -2 -1 0 1 2 3 У 4 2 1 Х -2 -1 0 1 2 3 У Х -2 -1 0 1 2 3 У
Слайд 7: Задание на оценку:
Заполните таблицу свойств показательной функции, опираясь на прошлые подобные таблицы и график показательной функции
Слайд 8
(-∞ ;+∞ ) ( 0;+∞) Ф-я общего вида Возрастает (- ∞ ;+ ∞ ) Снизу Свойства D(f) E(f) Чётность / нечётность Монотонность Ограниченность (-∞ ;+ ∞) ( 0 ;+∞) Ф-я общего вида Убывает (-∞ ;+∞ ) Снизу при a > 1 при 0 < a < 1
Слайд 9
- - Непрерывна Выпукла вниз (-∞ ;+∞ ) Симметрия относительно у=х у наибольшее у наименьшее Непрерывность Выпуклость / вогнутость Обратная ф-я - - Непрерывна Выпукла вниз (-∞ ;+∞) Симметрия относительно у=х Свойства при a > 1 при 0 < a < 1
Слайд 10: Показательная функция
При x=0 y =1 ( всегда) Та степень больше, показатель которой меньше Та степень больше, показатель которой больше
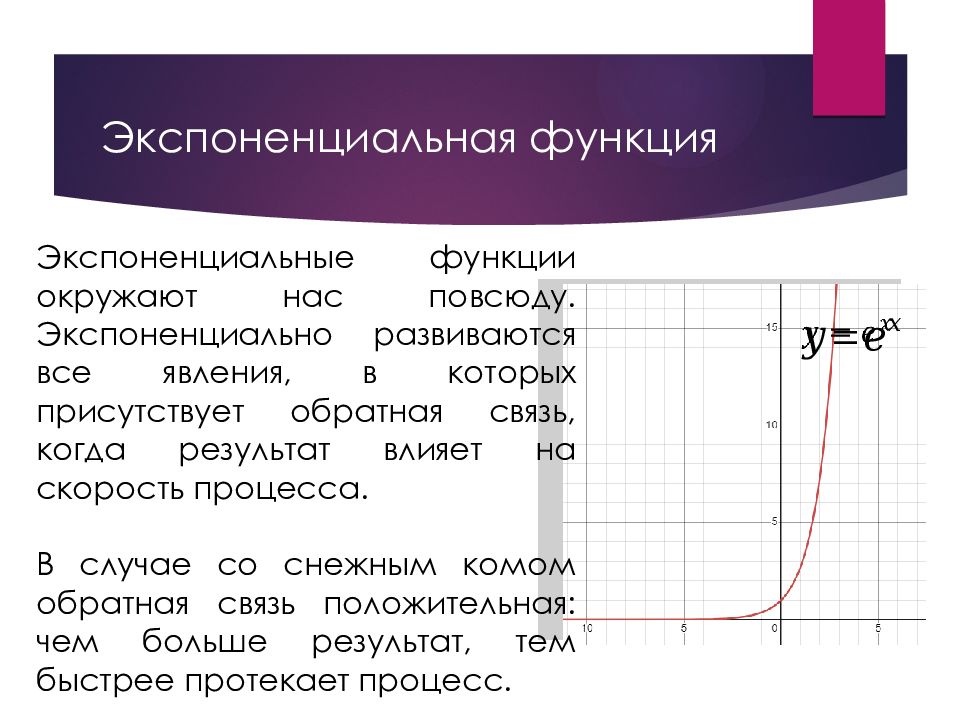
Слайд 11: Экспоненциальн ая функция
Основание показательной ф- ии – число e. Число Эйлера (число e) — математическая константа (действительное число), основание натурального логарифма. Приблизительно равно 2,718281828 …. Это иррациональное и трансцендентное число.
Слайд 13: Экспоненциальн ая функция
У экспоненциально протекающих процессов есть одно общее свойство: за одинаковый интервал времени их параметры меняются в одинаковое число раз. Банковский вклад каждый год увеличивается на 7%, снежный ком за минуту увеличивается в три раза, а количество урана-235 на атомных электростанциях уменьшается вдвое каждые 700 миллионов лет. Экспоненциальн ая функция
Слайд 14: Экспоненциальн ая функция
Экспоненциальные функции окружают нас повсюду. Экспоненциально развиваются все явления, в которых присутствует обратная связь, когда результат влияет на скорость процесса. В случае со снежным комом обратная связь положительная: чем больше результат, тем быстрее протекает процесс. Экспоненциальн ая функция
Слайд 16: Разработчиками ПО
Финансы : Показательная функция используется для расчета сложных процентов в финансовых приложениях. Например, чтобы узнать, сколько будет на счету через определенный период времени. 2. Биология и медицина: В биологии и медицине показательные функции используются для моделирования роста популяций организмов. Например, рост популяции бактерий часто описывается экспоненциальной функцией. 3. Математическое моделирование: Разработчики используют показательные функции для создания моделей физических процессов, таких как радиоактивный распад, распространение инфекционных заболеваний и другие явления, характеризующиеся быстрым ростом или убыванием.
Слайд 17: Разработчиками ПО
4. Информатика: При работе с алгоритмами сортировки, такими как быстрая сортировка ( Quicksort ), часто используется метод разделения массива по среднему элементу. Это позволяет уменьшить время выполнения алгоритма до логарифмического порядка, что значительно ускоряет процесс сортировки. 5. Теория вероятностей: Когда речь идет о случайных событиях, вероятность наступления которых зависит от времени, показательные функции играют важную роль. Например, если мы говорим о процессе возникновения ошибок в программном обеспечении.
Слайд 18: Разработчиками ПО
В контексте сортировки, показательная функция обычно используется для построения алгоритмов, которые эффективно работают на данных с определенными свойствами. Например, метод быстрой сортировки использует бинарный поиск для выбора пороговых значений, что позволяет быстро разделить массив на две части. Это уменьшает количество сравнений и операций обмена элементами, делая алгоритм эффективным для больших объемов данных.
Слайд 19: Графичсекими дизайнерами
Показательные функции могут использоваться графическими дизайнерами для создания различных эффектов, таких как увеличение яркости, контраста или насыщенности цветов. Например, они могут применять их для обработки фотографий или видеоматериалов. Показательные функции также могут быть полезны при создании специальных эффектов, таких как тени или свечения. Кроме того, они могут использоваться для настройки цвета и яркости в графических редакторах, таких как Adobe Photoshop или Illustrator.
Слайд 20: Домашняя работа (обязательно к выполнению) 1. Сравнить числа, используя свойства показательной функции :
Слайд 21: Домашняя работа (обязательно к выполнению) 2. Построить графики функций :
1) 2)