Слайд 3: Институт педагогики и психологии Кафедра психологии и коррекционной педагогики
М1.В.01.02 Методика обучения математике обучающихся с умственной отсталостью Мурманск 2024
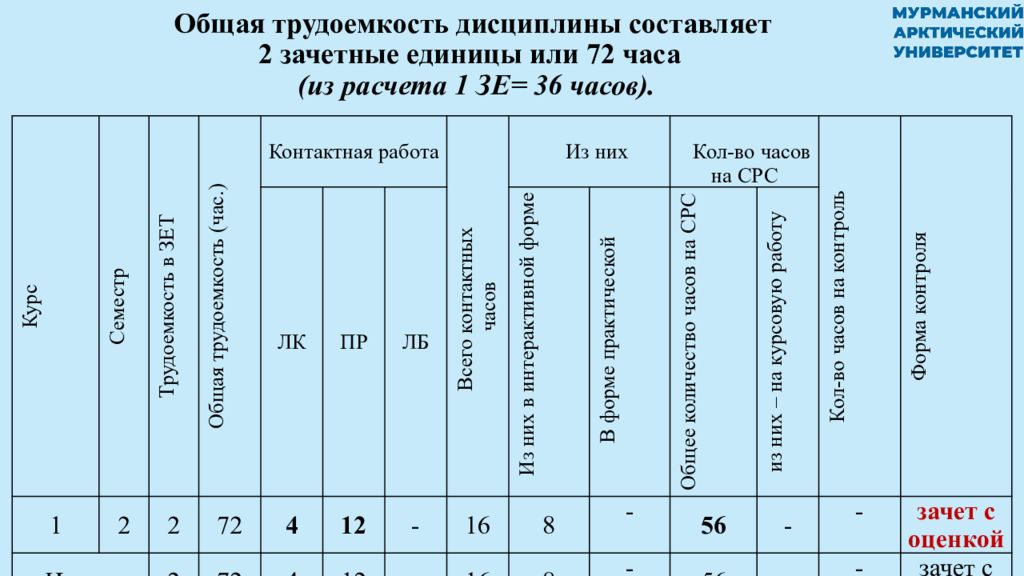
Слайд 4: Общая трудоемкость дисциплины составляет 2 зачетные единицы или 72 часа (из расчета 1 ЗЕ= 36 часов )
Курс Семестр Трудоемкость в ЗЕТ Общая трудоемкость (час.) Контактная работа Всего контактных часов Из них Кол-во часов на СРС Кол-во часов на контроль Форма контроля ЛК ПР ЛБ Из них в интерактивной форме В форме практической Общее количество часов на СРС из них – на курсовую работу 1 2 2 72 4 12 - 16 8 - 56 - - зачет с оценкой Итого: 2 72 4 12 - 16 8 - 56 - - зачет с оценкой
Слайд 5
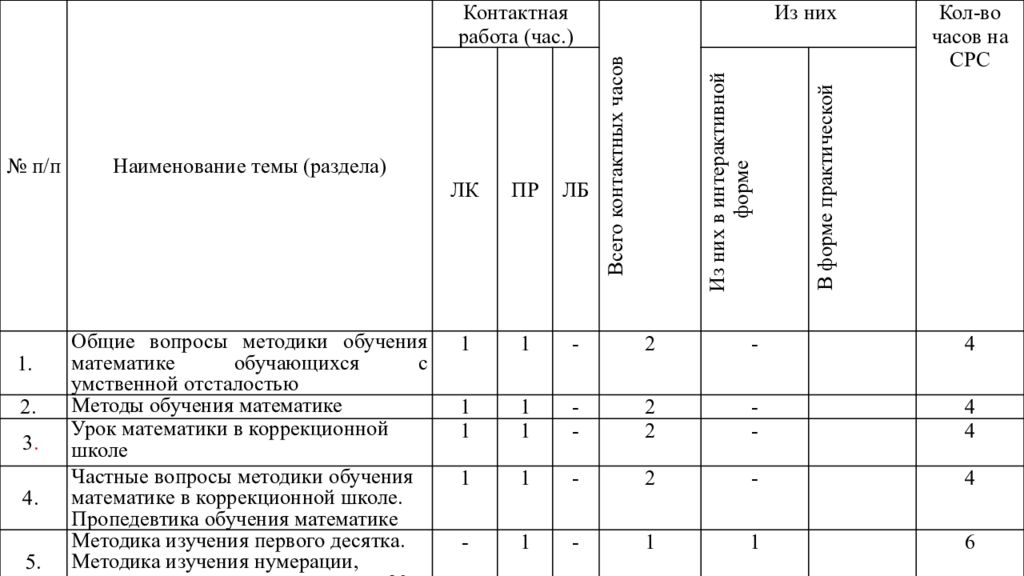
№ п/п Наименование темы (раздела) Контактная работа (час.) Всего контактных часов Из них Кол-во часов на СРС ЛК ПР ЛБ Из них в интерактивной форме В форме практической Общие вопросы методики обучения математике обучающихся с умственной отсталостью 1 1 - 2 - 4 2. Методы обучения математике 1 1 - 2 - 4 3. Урок математики в коррекционной школе 1 1 - 2 - 4 4. Частные вопросы методики обучения математике в коррекционной школе. Пропедевтика обучения математике 1 1 - 2 - 4 5. Методика изучения первого десятка. Методика изучения нумерации, сложения и вычитания в пределах 20 - 1 - 1 1 6 6. Методика изучения нумерации сложения и вычитания в пределах 100. Методика изучения табличного умножения и деления. - 1 - 1 1 6
Слайд 6
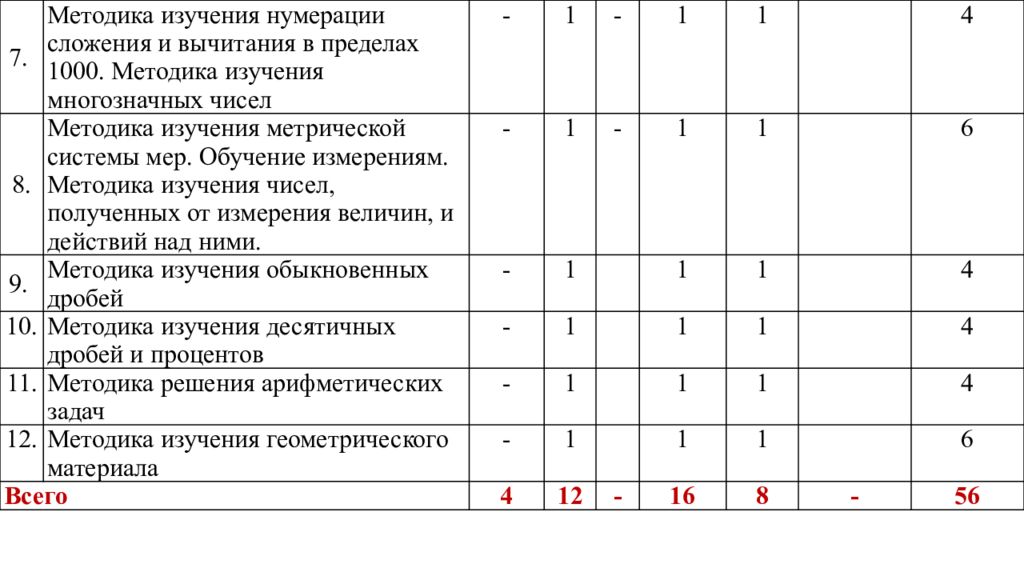
7. Методика изучения нумерации сложения и вычитания в пределах 1000. Методика изучения многозначных чисел - 1 - 1 1 4 8. Методика изучения метрической системы мер. Обучение измерениям. Методика изучения чисел, полученных от измерения величин, и действий над ними. - 1 - 1 1 6 9. Методика изучения обыкновенных дробей - 1 1 1 4 10. Методика изучения десятичных дробей и процентов - 1 1 1 4 11. Методика решения арифметических задач - 1 1 1 4 12. Методика изучения геометрического материала - 1 1 1 6 Всего 4 12 - 16 8 - 56
Слайд 7: Литература
1. Баряева Л.Б., Кондратьева С.Ю. Дискалькулия у детей: профилактика и коррекция нарушений в овладении счетной деятельностью. МЦНИП. Киров, 2013. 2. Лапп, Е. А. Коррекционная педагогика. Проектирование и реализация педагогического процесса : учебное пособие для бакалавриата и магистратуры / Е. А. Лапп, Е. В. Шипилова. — М. : Издательство Юрайт, 2017. — 147 с. — (Авторский учебник). — ISBN 978-5-534-00901-9. https://www.biblio-online.ru/book/C895D5A0-B538-4980-BD64-FB14F6CB95AE 3. Нигматов З. Г., Ахметова Д. З., Челнокова Т. А. Инклюзивное образование : история, теория, технология [Электронный ресурс] / Казань: Познание,2014. -220с. - 978-5-8399-0492-7 http://biblioclub.ru/index.php?page=book&id=257842 4. Перова М.Н. Методика преподавания математики в специальной (коррекционной) школе: Учеб. для студ. дефект. фак. педвузов. М.: Гуманит. изд. центр ВЛАДОС, 2001. – 408 с. 5. Формирование профессиональной компетентности педагога. Поликультурная и информационная компетентность: учебное пособие для вузов / Н. Р. Азизова, Н. А. Савотина, М. И. Бочаров, С. В. Зенкина. — М.: Издательство Юрайт, 2018. — 162 с. — (Серия : Образовательный процесс). — ISBN 978-5-534-06234-2. https://biblio-online.ru/book/F726AEEA-2FDD-418D-8B7E-014E76BFB345/formirovanie-professionalnoy-kompetentnosti-pedagoga-polikulturnaya-i-informacionnaya-kompetentnost. 6. Обучение математике в дошкольных образовательных организациях: Пособие / Белошистая А.В. - 2-е изд. - М.: НИЦ ИНФРА-М, 2016. - 320 с.: 60x90 1/16. - (Практическая педагогика) (Переплёт 7БЦ) ISBN 978-5-16-011419-4 http://znanium.com/bookread2.php?book=523771
Слайд 8: Дополнительная литература
1. Общеметодические аспекты обучения в специальных образовательных учреждениях: Учебно-методическое пособие / Матвеева М.В., Коршунова Т.В. - М.: Форум, НИЦ ИНФРА-М, 2016. - 176 с.: 60x90 1/16 (Обложка) ISBN 978-5-00091-136-5 http://znanium.com/bookread2.php?book=520623 2. Байдак, В. А. Теория и методика обучения математике: наука, учебная дисциплина [Электронный ресурс] : Монография / В. А. Байдак. - 2-е изд., стереотип. - М. : Флинта, 2011. - 264 с. http://znanium.com/bookread.php?book=405875 3. Новгородцева, И. В. Педагогика с методикой преподавания специальных дисциплин [электронный ресурс] : учеб. пособие модульного типа / сост. И.В. Новгородцева. - 2-е изд., стереотип. - М. : ФЛИНТА, 2011. - 378 с. // http://www.znanium.com/catalog.php?bookinfo=454525
Слайд 9: Тема 1. Общие вопросы методики обучения математике обучающихся с умственной отсталостью
Развитие методических основ преподавания математике в коррекционной школе. Задачи обучения математике обучающихся с умственной отсталостью. Связь обучения математики с другими учебными предметами. Особенности усвоения математических знаний, умений и навыков обучающимися с умственной отсталостью. Программа по математике в коррекционной школе.
Слайд 10: Тема 2. Методы обучения математике
Особенности использования методов обучения на уроках математики. Контроль качества знаний, умений и навыков.
Слайд 11: Тема 3. Урок математики в коррекционной школе
Основные требования к уроку математики в коррекционной школе. Система уроков математики. Виды уроков математики. Структура урока математики.
Слайд 12: Тема 4. Частные вопросы методики обучения математике в коррекционной школе. Пропедевтика обучения математике
Пропедевтика обучения математике. Формирование представлений и понятий о признаках величины предметов. Формирование понятий длинный – короткий, длиннее, короче, равные, разные по длине. Организация преподавания математики в подготовительный период.
Слайд 13: Тема 5. Методика изучения первого десятка. Методика изучения нумерации, сложения и вычитания в пределах 20
Понятия число и цифра. Обучение нумерации в пределах 10: (для всех по 2 числа выбрать. Составить конспекты уроков «Число и цифра….». Можно использовать книгу Волиной Праздник числа. Приветствуется использование ИКТ. Например, Игры для тигры и др.) Обучение нумерации в пределах 20. Обучение табличному умножению и делению в пределах 20.
Слайд 14: Тема 6. Методика изучения нумерации сложения и вычитания в пределах 100. Методика изучения табличного умножения и деления
Нумерация в пределах 100. Сложения и вычитания в пределах 100. Обучение табличному умножению и делению в пределах 100. Внетабличное умножение и деление.
Слайд 15: Тема 7. Методика изучения нумерации сложения и вычитания в пределах 1000. Методика изучения многозначных чисел
Нумерация в пределах 1000. Сложения и вычитания в пределах 1000. Методика изучения арифметических действий в пределах 1000. Методика изучения многозначных чисел. Трудности визуализации, представлений в реальном мире многозначных чисел. Методика сложения и вычитания многозначных чисел.
Слайд 16: Тема 8. Методика изучения метрической системы мер. Обучение измерениям. Методика изучения чисел, полученных от измерения величин, и действий над ними
Методика изучения метрической системы мер. Обучение измерениям. Методика изучения чисел, полученных от измерения величин, и действий над ними. Преобразование чисел, выражающих длину, массу, стоимость, время и др. Действия над числами, полученными от измерения величин
Слайд 17: Тема 9. Методика изучения обыкновенных дробей
Получение дробей. Преобразование дробей. Умножение и деление обыкновенных дробей. Нахождение одной и нескольких частей от числа. Нахождение числа от его одной части.
Слайд 18: Тема 10. Методика изучения десятичных дробей и процентов
Получение десятичных дробей. Сравнение десятичных дробей. Действия над десятичными дробями. Методика изучения процентов
Слайд 19: Тема 11. Методика решения арифметических задач
Методика решения простых арифметических задач. Трудности решения арифметических задач с косвенным вопросом Методика решения составных арифметических задач
Слайд 20: Тема 12. Методика изучения геометрического материала
Методика ознакомления обучающихся с умственной отсталостью с геометрическими фигурами связана с задачами изучения темы: формировать четкие представления о таких геометрических фигурах, как точка, отрезок, угол, многоугольник, прямоугольник, квадрат и. т.д.; формировать практические умения и навыки построения геометрических фигур, как с помощью чертёжных инструментов, так и без них; развивать пространственные представления обучающихся. Точка. Линия. Прямая и кривая линии. Отрезок. Углы. Прямой угол. Прямоугольник. Квадрат. Периметр прямоугольника и квадрата. Ломаная. Звенья ломаной. Длина ломаной. Луч. Треугольник. Равносторонний треугольник. Прямоугольный треугольник. Тупоугольный треугольник. Остроугольный треугольник. Представление о телах: куб, призма, пирамида, конус, цилиндр, шар и т.д.
Слайд 21: Тема 13. Исторический обзор и современное состояние методики развития математических представлений у дошкольников
1.1. Теория и методика математического образования дошкольника как научная и учебная дисциплина 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Слайд 22: Математическое образование дошкольников
Теория и методика математического образования дошкольников» является самостоятельной научной и учебной дисциплиной. Первоначально она существовала в рамках дошкольной педагогики, но накопив значительный эмпирический опыт, а также достаточно большой объем научной информации, постепенно превратилась в самостоятельную отрасль знаний. В системе педагогических наук она призвана способствовать интеллектуальному и всестороннему развитию ребенку с учетом неповторимости, уникальности, поддержки индивидуальных потребностей и интересов¸ ориентации на природный потенциал каждого ребенка.
Слайд 23: Предмет исследования
Предметом исследования дисциплины как научной области является изучение основных закономерностей процесса формирования и развития у дошкольников математических представлений и проектирование, осуществление на этой основе эффективных технологий развития и воспитания, способствующих познавательному, личностному развитию ребенка.
Слайд 24: Задачи, решаемые дисциплиной:
1. Научное обоснование целей, содержания, форм, методов предматематической подготовки в основных общеобразовательных программах дошкольного образования, требований к уровню развития количественных, пространственных, временных и др. представлений детей в разных возрастных группах; 2. Разработка и внедрение в практику современных эффективных, в том числе и компьютерных, технологий математического образования дошкольников; 3. Реализация преемственности в формировании основных математических понятий в детском саду и школе; 4. Разработка содержания и технологий, в том числе компьютерных, подготовки высококвалифицированных кадров, способных осуществлять математическое развитие детей с учетом отечественных и зарубежных достижений науки в разных формах дошкольного образования; 5. Разработка на научной основе методических рекомендаций родителям по развитию математических представлений у детей в условиях семьи.
Слайд 25: Теоретическая база
Теоретическую базу изучаемой дисциплины составляют не только общие, исходные положения философии, педагогики, психологии, математики и других наук. К ним относятся: - государственные документы по вопросам образования в РФ; - научные исследования и публикации, в которых отражены основные результаты научных поисков (статьи, монографии, сборники научных трудов и т.п.); - программно-методические документы; - методическая литература (статьи, пособия для воспитателей, родителей и т.п.); - инновационный педагогический опыт по развитию математических представлений в детском саду и семье, опыт и идеи передовых педагогов.
Слайд 26: Методика математического развития
Методика математического развития дошкольников постоянно развивается, совершенствуется и обогащается результатами научных исследований и инноваций. Регулярно выполняются и защищаются кандидатские и докторские диссертации.
Слайд 27: Методика математики
Дисциплина связана со многими науками и, прежде всего, с теми, которые изучают разные стороны личности ребенка, процесс его воспитания и развития. Наиболее тесная связь с дошкольной педагогикой. Эта дисциплина дает знание о принципах, условиях, содержании, методах, средствах, формах организации педагогического процесса в детском саду. Частные методики позволяют осуществлять интеграцию в обучении дошкольников: объединение математики и теории и методики развития речи, теории и методики физического воспитания, теории и методики музыкального воспитания и др., что способствует более полному усвоению математических представлений ребенком. Подготовка к усвоению математики в школе не может осуществляться без связи с методикой начального обучения математике. Наиболее продуктивными являются технологии, разработанные в системе детский сад – школа.
Слайд 28: Обучение математике должно строиться с учетом
закономерностей развития познавательной деятельности, личности ребенка, что является предметом изучением психологических наук. Восприятие, представление, мышление, речь не только функционируют, но и интенсивно развиваются в процессе обучения. Психологические особенности и закономерности восприятия ребенком множества предметов, чисел, пространства, времени служат основой при разработке методики формирования и развития математических представлений. Психология определяет возрастные возможности детей в усвоении знаний и умений, а также указывает пути сопровождения индивидуального маршрута математического развития ребенка. Рациональное построение процесса обучения связано с созданием оптимальных условий на основе анатомо-физиологических особенностей маленьких детей. Закономерности протекания физиологических процессов у дошкольников служат основой для определения форм, места и длительность обучения для каждого возраста детей.
Слайд 29: Связь … с другими предметами
Особо следует выделить связь с информатикой. Сегодня разработаны специальные программы по информатике для дошкольников. Организуются специальные компьютерные среды для обучения детей математике. Связь с различными науками создает теоретическую базу методики развития математических представлений.
Слайд 30: 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Первый этап – эмпирическое развитие методики. Вопросы математического развития детей своими корнями уходят в классическую и народную педагогику. Различные считалки, пословицы, поговорки, загадки, потешки были хорошим материалом в обучении детей счету, позволяли сформировать у ребенка понятия о числах, форме, величине и т.д. Позднее на этом этапе произошло выдвижение идеи о необходимости математического развития детей дошкольного возраста. Выдающиеся мыслители прошлого (Я.А Коменский, И.Г. Песталоцци, К.Д.Ушинский, Л.Н. Толстой), видные деятели (М. Монтессори, Ф.Фребель ) осознавали, что без предварительной математической подготовки детям будет трудно осваивать школьную программу.
Слайд 31: 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Второй этап – Начальный этап становления теории и методики математического развития дошкольников. Определение содержания, методов и приемов работы с детьми, дидактических материалов. Исторически этот этап относится к 20-30 годам 20-го века. Большую роль сыграли отдельные педагоги-исследователи: Е.И. Тихеева, Ф.Н. Блехер, Л.В. Глаголева и др.), «школ» и направлений сенсорного воспитания (М. Монтесори, А.В. Венгер). С начала 20 века в России начала создаваться научно-обоснованная дидактическая система обучения дошкольников математике. Ее начальный этап – начало 20 века – 40-е годы 20 века. В это время в дореволюционной России методические пособия адресовывались, как правило, одновременно семье и д/с. В них родители и воспитатели знакомились с содержанием обучения математике детей. В 1912 голу выходит пособие В.А.Кемниц «Математика в д/с»: игры, беседы, упражнения, изучение чисел 1-10, действий с ними, форм, величин, измерения, части и целого. До 1939 г. в д/с Ленинграда детей обучали счету по методике Л.В.Глаголевой, в которой она рекомендовала опираться на обе господствующие в то время теории: восприятия числа путем счета и путем образа. Она пропагандировала разнообразие методов: • лабораторный (отработка практических действий с использованием наглядных материалов) • исследовательский (поиск детьми ситуаций применения знаний, аналогичных изучаемым) • иллюстративный (закрепление умений в продуктивной деятельности) • наглядный • игра. Кроме того, Л.В. Глаголева раскрыла приемы формирования представлений о величинах, измерении, делении целого на части.
Слайд 32: 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Третий этап. П родолжался с 50х годов 20 века. Создание научно обоснованной дидактической системы формирования элементарных математических представлений в дошкольном возрасте: определение содержания, методов и приемов работы с детьми, дидактических материалов. А.М. Леушина изучала теорию и методику развития количественных и числовых представлений у детей в процессе обучения. 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Слайд 33: 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Четвертый этап – Психолого-педагогические исследования 60-70 годов 20 века. Изучались закономерности становления представлений о числе, развития счетной деятельности, вычислительной деятельности. Обосновывалась необходимостью начинать обучение детей с раннего возраста, с восприятия множеств предметов, с последующим обучением счету, выделению отношений между числами. Разрабатывались дидактические материалы, пособия, игры. Это были исследования психологов: И.А Френкеля, Л.Ф. Яблокова, Н.А. Менчинской, Н.Н. Лежавы, Г.С. Костюка. Педагогов: А.М. Леушиной, Н.Г. Бакст. В 70-80 годы проведены исследования по отдельным проблемам методики (Т.В. Тарунтаева, В.В. Данилова, Г.А. Корнилова, Т.Д. Рихтерман ). 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Слайд 34: 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Пятый этап – современное состояние теории и методики математического развития детей дошкольного возраста. С 80х годов 20 века до настоящего времени. Современное состояние теории и методики развития математических представлений у детей дошкольного возраста сложилось в 80-90 годы и первые годы нового столетия под влиянием развития идей обучения детей математике, а также реорганизации всей системы образования. Уже в 80 годы начали обсуждаться пути совершенствования как содержания, так и методов обучения дошкольников математике. В качестве негативного момента отмечалась ориентировка на выработку у детей предметных действий, в основном связанных со счетом и простейшими вычислениями, без должного уровня их обобщенности. Такой подход не обеспечивал подготовку к усвоению математических понятий в дальнейшем обучении. Специалисты изучали возможности интенсификации и оптимизации обучения, способствующие общему и математическому развитию ребенка, отмечали необходимость повышения теоретического уровня осваиваемых детьми знаний. Это требовало реконструкции программы обучения. Начались поиски путей обогащения содержания обучения. Решение этих сложных задач осуществлялось по-разному. 1.2. Исторические этапы становления и развития «Теории и методики математического образования дошкольника»
Слайд 36: Литература
1. Формирование элементарных математических представлений у дошкольников. Под ред. А.А. Столяра. -М.,- Просвещение, 1988. 2. Леушина А.М. Формирование элементарных математических представлений у детей дошкольного возраста. М., 1974. 3. Щербакова Е.И. Методика обучения математике в детском саду. М., 2000. 4. Щербакова Е.И. Теория и методика математического развития дошкольников. – М., 2005. 5. Грин Р., Лаксон В. Введение в мир числа. – М., 1974 6. Альтхауз Д., Дум Э. Цвет, форма, количество. – М., 1984 7. Фидлер М Математика уже в детском саду. – М, 1981. 8. Доман Глен, Доман Дженет Как обучить ребенка математике. – М., 1996. 9. Мак- Гован Д., Шрутен М. Играем в математику!- Мн, 2005.
Слайд 37
Основная 1. Михайлова З.А. и др. Теории и технологии математического развития детей дошкольного возраста. – СПб.: «ДЕТСТВО-ПРЕСС», 2008.- 384с. 2. Щербакова Е.Н. Теория и методика математического развития дошкольников. – М.: Издательство Московского психолого-социального института; Воронеж: Издательство НПО «МОДЭК», - 2005.-392с. Дополнительная 1. Егоров С.Ф., Лыков С.В.. Волобуева Л.М. Введение в историю дошкольной педагогики/Под ред. С.Ф. Егорова. – М.: «Академия» -2001.-390с. 2. Теории и технологии математического развития детей дошкольного возраста. Хрестоматия /сост. З.А. Михайлова, Р.Л. Непомнящая, М.Н. Полякова. - СПб, 2006. 3. Формирование элементарных математических представлений у дошкольников / Под ред. А.А. Столяра. - М., 1988.
Слайд 38: Глоссарий
Предмет исследования дисциплины как научной области является изучение основных закономерностей процесса формирования и развития у дошкольников математических представлений и проектирование, осуществление на этой основе эффективных технологий развития и воспитания, способствующих познавательному, личностному развитию ребенка. Теоретическая база исследования методики математического образования дошкольников – общие исходные положения философии, педагогики, психологии, математики и др. наук.
Слайд 39: Глоссарий
В современном словаре иностранных слов находим такое определение термина « формировать» [лат. formare ] 1 ) образовывать, составлять, организовывать; 2 ) придавать чему-либо какую-либо форму, вид, законченность; порождать. Анализ педагогических источников позволил сделать вывод о том, что формирование – изменения в развитии личности человека или отдельных его качеств, которые происходят под влиянием совокупности факторов: внутренних и внешних, природных и социальных, объективных и субъективных. Формировать – это организовывать всю жизнедеятельность человека, осуществлять воспитание и обучение, воздействовать на него так, чтобы развить то или иное качество.
Слайд 40: Глоссарий
Развитие – философская категория, выражающая процесс движения, изменения целостных систем. К наиболее характерным чертам развития относятся: возникновение качественно нового объекта (или его состояния), направленность, необратимость, закономерность, единство количественных и качественных изменений, взаимосвязь прогресса и регресса, противоречивость, спиралевидность формы (цикличность), развертывание во времени. Развитие - это изменение, представляющее собой переход качества от простого ко все более сложному, от низшего к высшему; процесс, в котором постепенное накопление количественных изменений приводит к наступлению качественных изменений. Являясь процессом обновления, рождения нового и отмирания старого, развитие противоположно регрессу, деградации. Источником и внутренним содержанием развития является наличие противоречий между старым и новым.
Слайд 41: Глоссарий
В психолого - педагогической литературе определилось два подхода к рассматриваемым дефинициям. Первый — формирование личности как ее развитие, т.е. процесс и результат этого развития. Взятое в этом значении понятие формирования личности является предметом психологического изучения, в задачу которого входит выяснение того, что есть (находится в наличии, экспериментально выявляется, обнаруживается) и что может быть в развивающейся личности в условиях целенаправленных воспитательных воздействий.Это собственно психологический подход к формированию личности. Второй смысл - формирование личности как ее целенаправленное воспитание. А.С. Макаренко удачно назвал этот процесс «проектированием личности». Это собственно педагогический подход к вычленению задач и способов формирования личности. Педагогический подход предполагает необходимость выяснить, что и как должно быть сформировано в личности, чтобы она отвечала требованиям, которые предъявляет к ней общество. Нельзя допускать смешения психологического и педагогического подхода к формированию личности, в противном случае может произойти подмена желаемым действительного. Синтезируя наиболее устоявшиеся определения, приходим к выводу, что развитие — это процесс и результат количественных и качественных изменений в организме человека. Оно связано с постоянными, непрекращающимися изменениями, переходами из одного состояния в другое, восхождением от простого к сложному, от низшего к высшему. В человеческом развитии проявляется действие универсального философского закона взаимоперехода количественных изменений в качественные и наоборот. Глоссарий
Слайд 42: Глоссарий
Математика – наука абстрактная, для ее понимания требуется развитое словесно-логическое мышление. У дошкольника пока еще преобладает наглядно-образное, мышление на уровне представлений. 24 Представления, в том числе и математические, - это субъективные образы объективно существующие, воссозданные памятью или созданные воображением, возникающие, когда нечто материальное, породившее эти образы, непосредственно не воздействует на органы чувств субъекта. Генетически представления занимают прмежуточное положение между восприятием и понятиями. Представления предшествуют понятийному мышлению, сопровождают его, придают понятийному мышлению конкретность и определенность. Исследования педагогов и психологов (Ж.. Пиаже, Л.С. Выготский, А.В. Запорожец, Л.А. Венгер, А.М. Леушина, Г.А. Корнеева, Е.И. Щербакова, В.В. Данилова, Т.А. Мусейибова и др.) показывают, что существуют особенности восприятия и генезиса математических представлений в дошкольном возрасте. Глоссарий
Слайд 43: Глоссарий
Математическое образование направлено на освоение дошкольниками представлений, которые являются предпосылкой формирования математических понятий (число, величина, геометрические фигуры). Математические представления (о множестве, числе, счете, форме предметов и геометрических фигурах, величинах и их измерении, простейших вычислениях), постигаемые ребенком на эмпирическом, чувственном уровне, называют элементарными. Глоссарий
Слайд 44: Глоссарий
Формирование элементарных математических представлений – это целенаправленный процесс передачи и усвоения знаний, приемов и способов умственной деятельности, предусмотренных программными требованиями. Основная его цель – не только подготовка к успешному овладению математикой в школе, но и всестороннее развитие детей. Формирование элементарных математических представлений дошкольников осуществляется с помощью научно обоснованной методической системы, компонентами которой являются цель, содержание, методы, средства и формы организации работы, теснейшим образом связанных между собой и взаимообусловленных друг другом. Глоссарий
Последний слайд презентации: Математика УО ГОЛ: Глоссарий
Среди задач по формированию элементарных математических знаний и последующего математического развития детей следует выделить главные, а именно: приобретение знаний о множестве, числе, величине, форме, пространстве и времени как основы математического развития; формирование широкой начальной ориентации в количественных, пространственных и временных отношениях окружающей действительности; формирование навыков и умений в счете, вычислениях, измерении, моделировании, общеучебных умений; овладение математической терминологией; развитие познавательных интересов и способностей, логического мышления, общее интеллектуальное развитие ребенка. Глоссарий