МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ Общие сведения о местных сопротивлениях
Гидравлические потери энергии - местные потери и потери на трение по длине. Рассмотрим более подробно потери, обусловленные местными сопротивлениями, т. е. элементами трубопроводов, в которых из-за изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв транзитного потока от стенок русла и возникают вихреобразования. Ранее были приведены примеры местных сопротивлений и эмпирическая общая формула связи местной потери напора и скорости потока - формула Вейсбаха:
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местных сопротивлений представляют собой соединения или комбинации перечисленных простейших сопротивлений. Так, например, при течении жидкости через вентиль поток искривляется, меняет свое направление, сужается и, наконец, расширяется до первоначальных размеров ; при этом возникают интенсивные вихреобразования.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе. Коэффициенты потерь при турбулент ном течении определяются в основном формой местных сопротивлений и очень мало изменяются с изменением абсолютных размеров русла, скорости потока и вязкости ν жидкости, т. е. с изменением числа Re, поэтому обычно принимают, что они не зависят от Re, что означает квадратичный закон сопротивления, или автомодельность.
Внезапное расширение русла (канала, трубы)
Значения коэффициентов чаще получают из опытов, на основании которых выводят эмпирические формулы или строят графики. Для внезапного расширения при турбулентном течении потерю напора можно найти теоретическим путем. Поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии.
Рис. Внезапное расширение трубы
При этом происходит непрерывный обмен частицами Ж между основным потоком и завихренной его частью. Основной вихрь порождает более мелкие вихри, которые уносятся потоком и при этом распадаются на еще более мелкие вихри. Таким образом, потеря энергии происходит не только в основном вихре, но и по длине следующего за ним участка потока.
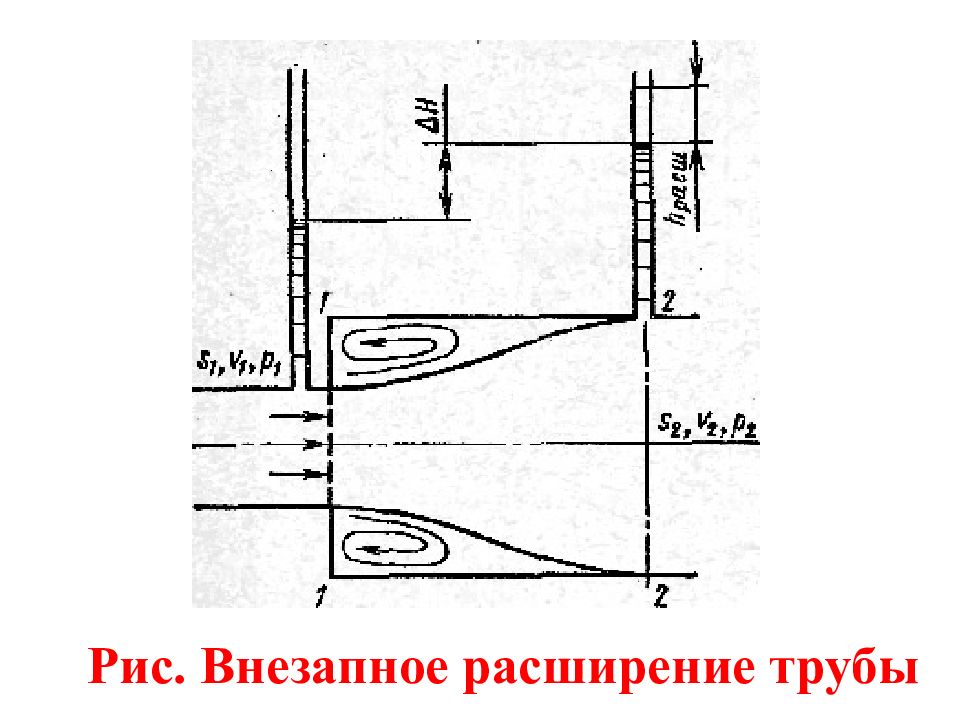
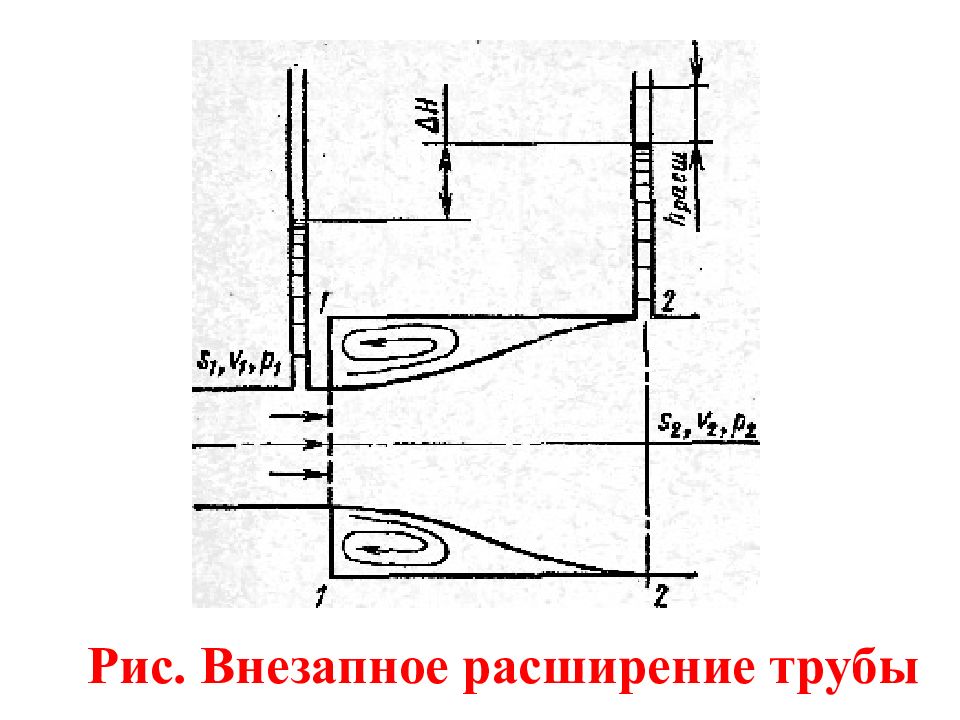
Рассмотрим два сечения горизонтального потока: 1—1 - в плоскости расширения трубы и 2—2 - после расширения, где поток заполнил все сечение широкой трубы. Так как поток между сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту, на большую, чем первый ; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на h расш. Эта высота h расш и есть местная потеря напора на расширение.
Рис. Внезапное расширение трубы
Давление, скорость, площадь потока в сеч. 1-1 - р 1, υ 1, S 1 ; в сеч. 2 - 2 - р 2, υ 2, S 2. Сделаем три допущения: 1) распределение скоростей в сеч. 1-1 и 2-2 равномерное (т. е. 1 = 2 =1, что обычно принимается при турбулентном режиме); 2) касательное напряжение на стенке трубы между сеч. 1-1 и 2-2 равно нулю, т. е. пренебрегаем силой трения (мала по сравнению с силами давления; 3) давление р 1 в сеч. 1-1 действует по всей площади S 2 потому, что, хотя труба и расширилась, поток в сеч. 1 - 1 еще сохранил свой поперечный размер, следовательно, υ 1 и р 1 еще не изменились.
Запишем для сеч. 1-1 и 2 - 2 уравнение Бернулли с учетом потери напора h pa сш на расширение (принимая z 1 = z 2 = 0):
Применим теорему Эйлера об изменении количества движения к фиксированному объему, заключенному между сечениями 1-1, 2-2 и стенкой трубы. Для этого определим равнодействующую внешних сил, действующих на рассматриваемый объем в направлении движения, т. е. сил давления. Т.к. площади оснований цилиндра слева и справа одинаковы и равны S 2, давление p 1 в сечении 1 - 1 равномерно распределено по всей площади S 2, равнодействующая сила численно равную секундному импульсу ( p 1 – p 2 ) S 2.
Соответствующее этому импульсу изменение количества движения найдется как разность между секундным количеством движения, выносимым из рассматриваемого объема и вносимым в него: Q ρ ( υ 2 – υ 1 ); (при равномерном распределении скоростей по сечениям). Приравняем одно к другому по теореме Эйлера: ( p 1 – p 2 ) S 2 = Q ρ ( υ 2 – υ 1 ).
Разделим это уравнение на S 2 ρ g ; преобразуем правую часть уравнения, учитывая, что Q = υ 2 S 2 :
Сгруппируем и получим Это уравнение полностью аналогично ранее записанному уравнению Бернулли и тогда h расш = ( υ 1 – υ 2 ) 2 /(2 g ), (1.70) т. е. потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей (теорема Борда в честь французского ученого, который в 1766 г. вывел эту формулу.
Следовательно, для внезапного расширения русла = ( l – S 1 / S 2 ) 2. Если учесть, что υ 1 S 1 = υ 2 S 2, то полученный результат можно записать еще в виде, соответствующем общему способу выражения местных потерь : (1.70′) (1.71)
Доказанная теорема хорошо подтверждается опытом при турбулентном течении и широко используется в расчетах. Когда площадь S 2 S 1 и, следовательно, скорость υ 2 0 ( можно считать равной нулю), h расш = υ 1 2 /(2 g ), т. е. теряется весь скоростной напор (вся кинетическая энергия, которой обладает жидкость ); =1. Такому случаю соответствует, например, подвод жидкости по трубе к резервуару достаточно больших размеров.
Потеря напора (энергии) при внезапном расширении расходуется на вихреобразование, связанное с отрывом потока от стенок, т. е. на поддержание непрерывного вращательного движения жидких масс с постоянным их обновлением (обменом). Поэтому этот вид потерь, пропорциональных скорости (расходу) во второй степени, называют потерями на вихреобразование. В конечном счете они расходуются на работу сил трения, но не непосредственно, как в прямых трубах постоянного сечения, а через вихреобразование.
Постепенное расширение русла
Диффузор (Д) - постепенно расширяющаяся труба. Течение Ж в Д сопровождается уменьшением υ и увеличением p, а следовательно, преобразованием кинетической энергии Ж в энергию давления. Частицы движущейся Ж преодолевают нарастающее давление за счет своей кинетической энергии, которая уменьшается вдоль Д и, что особенно важно, в направлении от оси к стенке.
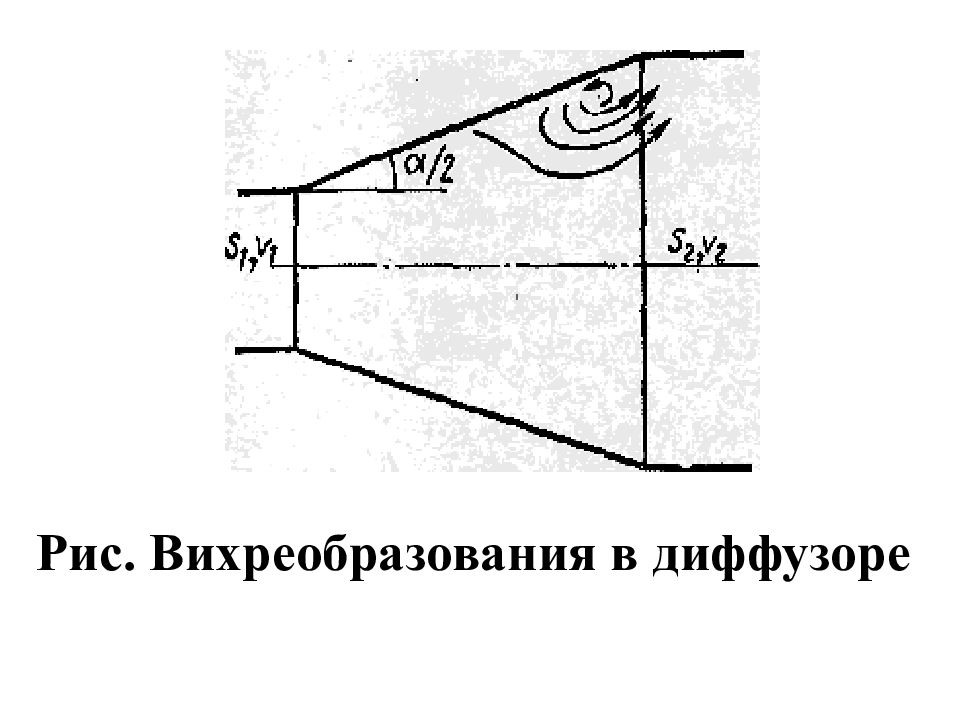
Слои Ж, прилежащие к стенкам, обладают столь малой кинетической энергией, что иногда не в состоянии преодолеть повышенное давление, останавливаются или даже начинают двигаться обратно. Обратное движение (противоток) вызывает отрыв основного потока от стенки и вихреобразования (рис.). Интенсивность явлений возрастает с увеличением угла расширения Д, а вместе с этим растут потери на вихреобразования.
Рис. Вихреобразования в диффузоре
Кроме того, в Д имеются обычные потери на трение, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора h диф в Д условно рассматривают как сумму двух слагаемых: h диф = h тр + h расш, где h тр и h расш – потери напора на трение и расширение (на вихреобразование). (1.72)
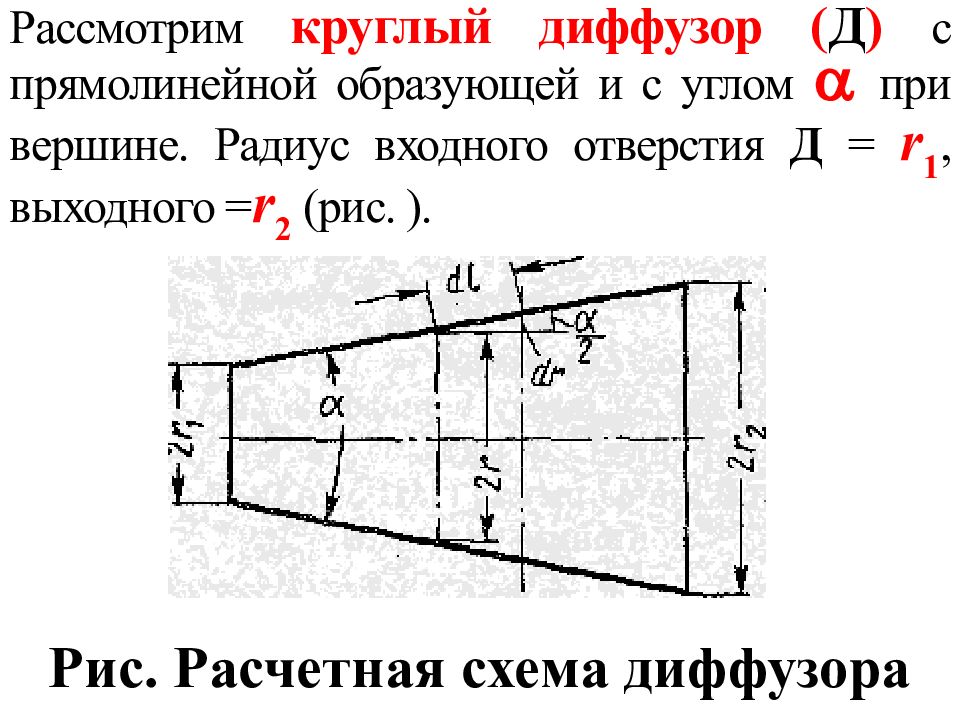
Рассмотрим круглый диффузор ( Д ) с прямолинейной образующей и с углом при вершине. Радиус входного отверстия Д = r 1, выходного = r 2 (рис. ). Рис. Расчетная схема диффузора
h тр можно приближенно подсчитать следующим способом. Так как r сечения и υ движения Ж - величины переменные вдоль Д, то элементарная потеря напора на трение для элементарного отрезка Д длиной dl вдоль образующей выразится по основной формуле гд e υ - средняя скорость в произвольно взятом сечении, радиус которого r. Из элементарного треугольника: dl = dr / sin ( /2). (1) (*)
На основании уравнения расхода можно записать υ = υ 1 ( r 1 / r ) 2, (2) где υ 1 - скорость в начале Д. Подставим выражения (1) и (2) в (*) для dh тр и выполним интегрирование в пределах от r 1 до r 2, (вдоль всего Д ), считая т постоянным:
или где п= ( S 2 / S 1 )=( r 2 / r 1 ) 2 - степень расширения Д. (1.73)
Второе слагаемое - потеря напора на расширение (на вихреобразование) – имеет ту же природу, что и при внезапном расширении, но меньшее значение, поэтому оно обычно выражается по формуле ( 1.70) или ( 1.71), но с поправочным коэффициентом k < 1, (1.74)
Коэффициент k называют коэффициентом смягчения (в Д по сравнению с внезапным расширением торможение потока как бы мягче). Значение k для Д с углами конусности =5 - 20° можно определять по формуле k = sin . (1.75) Учитывая полученные формулы (1.73) и (1.74), можно исходное выражение (1.72 h диф = h тр + h расш ), записать в виде (1.76)
а коэффициент ζ сопротивления Д выразить формулой (1.77) Это выражение показывает, что коэффициент ζ диф зависит от угла , коэффициента т и степени расширения п.
Выясним характер зависимости ζ диф от . С увеличением при заданных т и п первое слагаемое (обусловленное трением) в формуле (1.77), уменьшается, так как Д становится короче, а второе слагаемое ( обусловленное вихреобразованием и отрывом потока ) увеличивается. При уменьшении вихреобра зование уменьшается, но возрастает трение, так как при заданной п диффузор удлиняется, и поверхность его трения увеличивается.
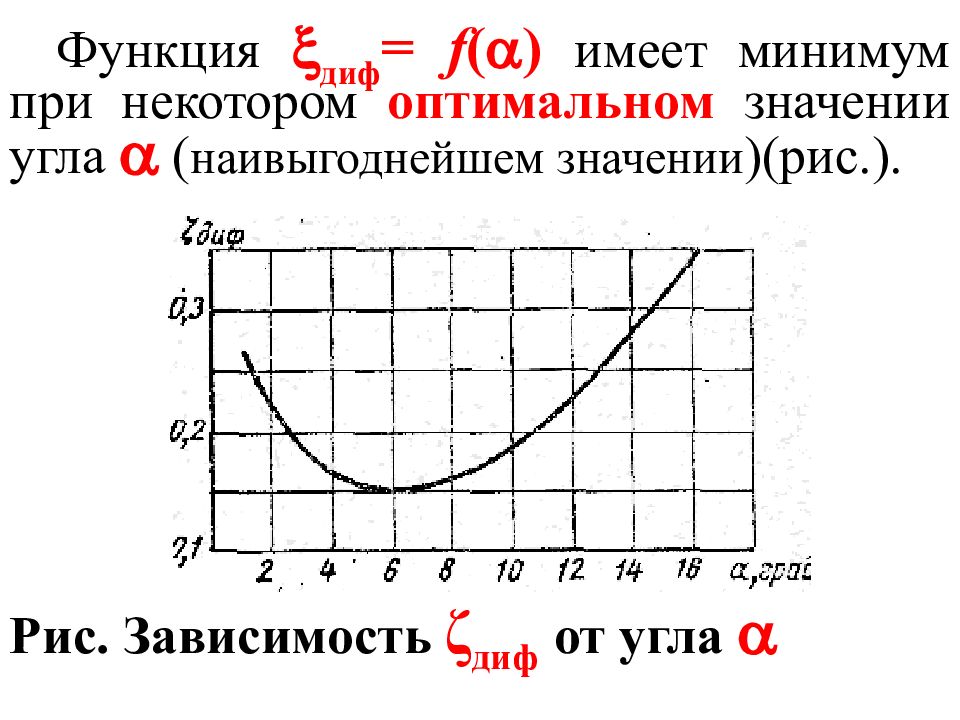
Функция диф = f ( ) имеет минимум при некотором оптимальном значении угла ( наивыгоднейшем значении ) (рис. ). Рис. Зависимость ζ диф от угла
Значение опт можно приближенно найти следующим способом: в (1.77) заменим sin ( /2) через sin /2, продифференцируем полученное выражение по , приравняем к «0» и решим относительно . Найдем откуда получим опт
При подстановке в эту формулу т = 0,015-0,025 и п =2-4 получим опт =6°, что соответствует экспериментальным данным. Для сокращения длины Д при заданном п на практике обычно принимают = 7- 9° (такие же углы и для квадратных диффузоров). Для прямоугольных Д с расширением в одной плоскости (плоские диффузоры) опт больше, чем для круглых и квадратных, и составляет 10-12°.
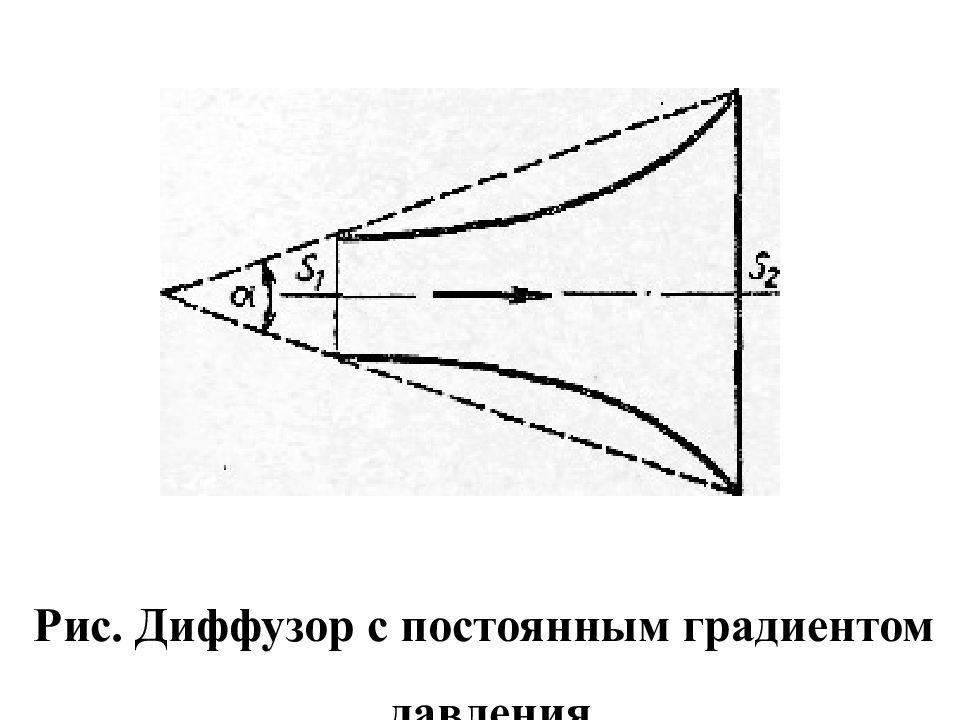
Если габариты не позволяют установить углы , близкие к опт, то при >15-25° целесообразно отказаться от Д с прямолинейной образующей и применить один из специальных Д, например, Д, обеспечивающий постоянный градиент р вдоль оси ( dp / dx = const ) и, следовательно, приблизительно равномерное нарастание р (при прямой образующей градиент р убывает вдоль Д) (рис.).
Рис. Диффузор с постоянным градиентом давления
Уменьшение потери энергии в таких Д по сравнению с обычными будет тем больше, чем больше угол , и при углах 40 - 60° доходит до 40 % от потерь в обычных Д. Кроме того, поток в криволинейном Д отличается большей устойчивостью, т. е. в нем меньше тенденций к отрыву потока.
Хорошие результаты дает также ступенчатый Д, состоящий из обычного Д с опт и следующего за ним внезапного расширения (рис.), которое не вызывает больших потерь энергии, так как скорости в этом месте сравнительно малы. Общее сопротивление такого Д значительно меньше, чем обычного Д такой же длины, и с той же степенью расширения, показанного на рисунке штриховыми линиями. Рис. Ступенчатый диффузор
