Первый слайд презентации: Множество, подмножество
Цели: и зучить, что такое множество и подмножество, рассмотреть примеры., что являемся дополнением множества, у читься решать задачи на множества Множество, подмножество Ключевые слова : Множество Способы задания множеств Знак принадлежности множеству Пустое множество Подмножество Числовые множества Свойства множеств
Слайд 2
«Множество есть многое, мыслимое нами как единое» основатель теории множеств – Георг Кантор (1845—1918) — немецкий математик, логик, теолог, создатель теории бесконечных множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв. Множество, подмножество
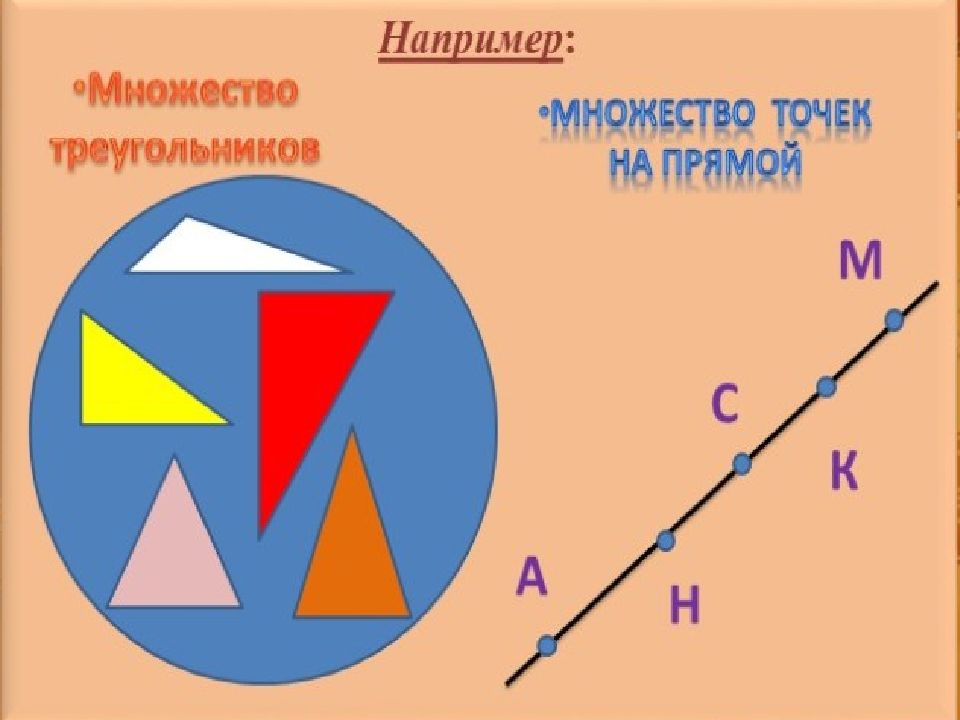
Слайд 3: Примеры множеств из окружающего мира
Например, множество дней недели состоит из элементов : понедельник, вторник, среда, четверг, пятница, суббота, воскресенье. Множество месяцев – из элементов : январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Слайд 6
Множество можно задать одним из двух способов: Можно явно перечислить все элементы множества. (Н-р, дни недели) Можно описать множество, т.е. указать признак, которым обладают все элементы множества (кубик с цифрами 1,2,3,4,5,6) Множество – это совокупность объектов, объединённых каким-либо признаком, свойством
Слайд 7: Условные обозначения
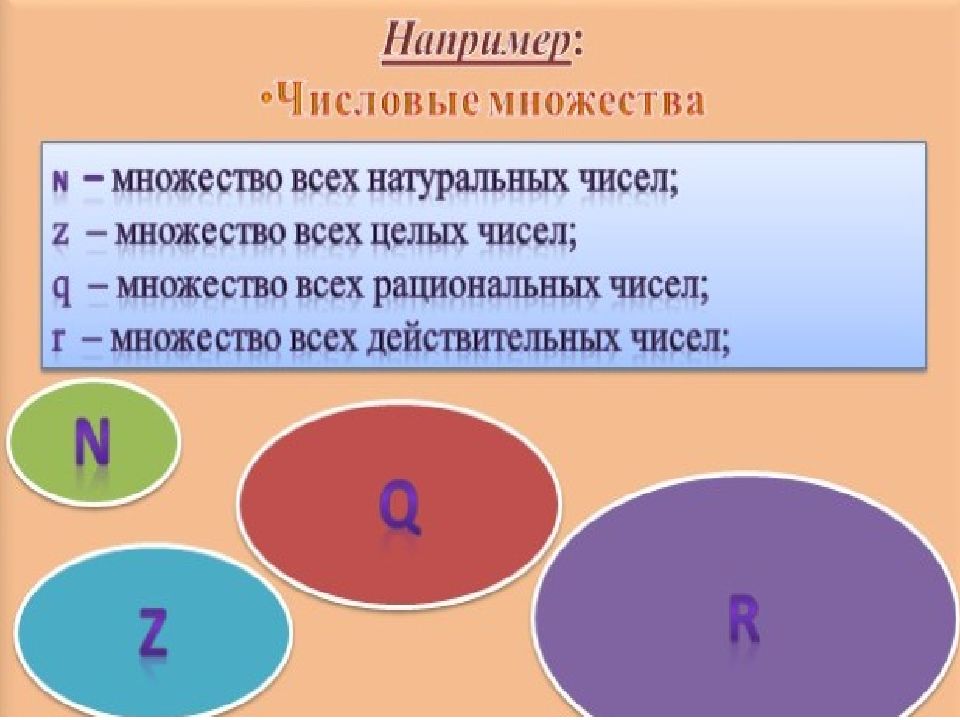
Множества: Заглавные буквы латинского алфавита или их сочетание: N, Z, GR,… Графическое изображение – круги Эйлера, диаграммы Венна Элементы множества: строчные буквы латинского алфавита: a, b, c,… н атуральное изображение элемента множества: 5, лисица,, …… Принадлежность элементов множеству: «а принадлежит множеству А » - а ∈ А «а не принадлежит множеству А» - а ∉ А
Слайд 8
Чтобы указать, что некоторый элемент принадлежит множеству, используют значок Например: А, читается « 6 принадлежит А» А, читается «7 не принадлежит А»
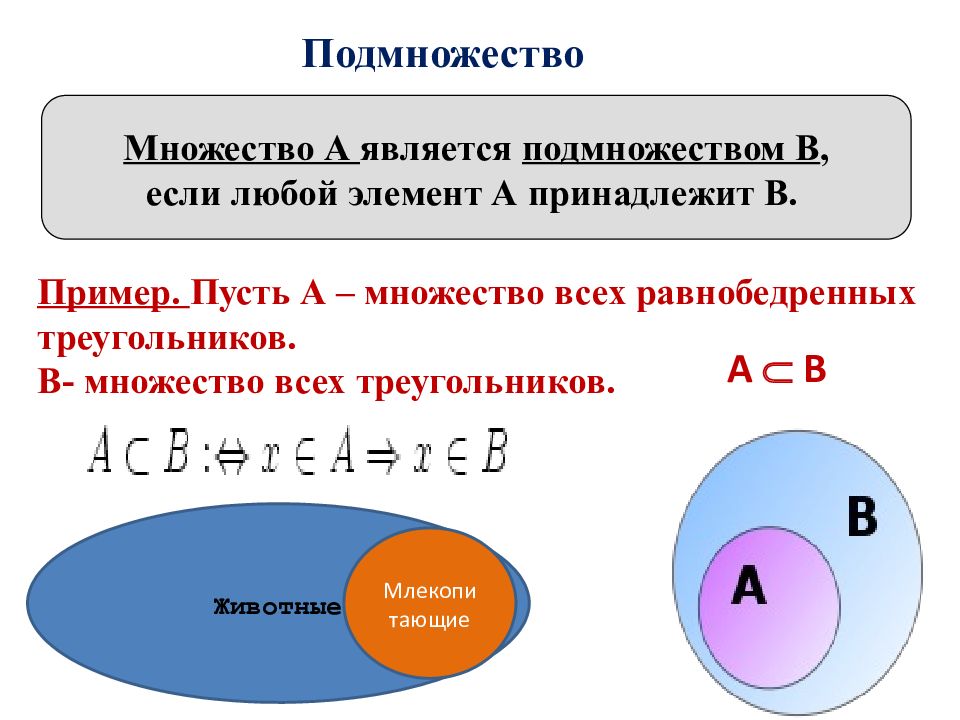
Слайд 10: Подмножество
Пример. Пусть А – множество всех равнобедренных треугольников. В- множество всех треугольников. Множество А является подмножеством В, если любой элемент А принадлежит В. Животные Млекопитающие А В
Слайд 11
Равные множества Два множества A и B будут равны, если каждый элемент A будет также являться элементом B, и каждый элемент множества B будет также являться элементом A: a b c d e Рассмотрим 2 множества: А={ a, b, c, d, e } В ={ c, d, a, b, e } Множества А и В называются равными, если А ⊂ В и В ⊂ А Эти множества пересекаются, причем каждый элемент множества А является элементом множества В (А ⊂ В), и наоборот, каждый элемент множества В является элементом множества А (В ⊂ А). А = В
Слайд 12
Пустое множество является подмножеством любого множества Пустое множество Пустое множество – это множество которое не содержит элементов. Любое множество является подмножеством самого себя.