Первый слайд презентации: Надо подчинить свои чувства исполнению долга» Священные писания
Слайд 2: Задание
Найти все правила по каждой теме (из файла «стереометрия вся теория»), записать их в тетрадь, добавив чертёж (его можно найти в интернете). Темы: Параллельные прямая и плоскость Параллельные плоскости Тетраэдр и его элементы Параллелепипед и его элементы Построение основных сечений (правила и понять как строить)
Слайд 4: Взаимное расположение прямой и плоскости
Возможны три случая взаимного расположения прямой и плоскости в стереометрии: Прямая лежит в плоскости (каждая точка прямой лежит в плоскости). Прямая и плоскость пересекаются (имеют единственную общую точку). Прямая и плоскость не имеют ни одной общей точки.
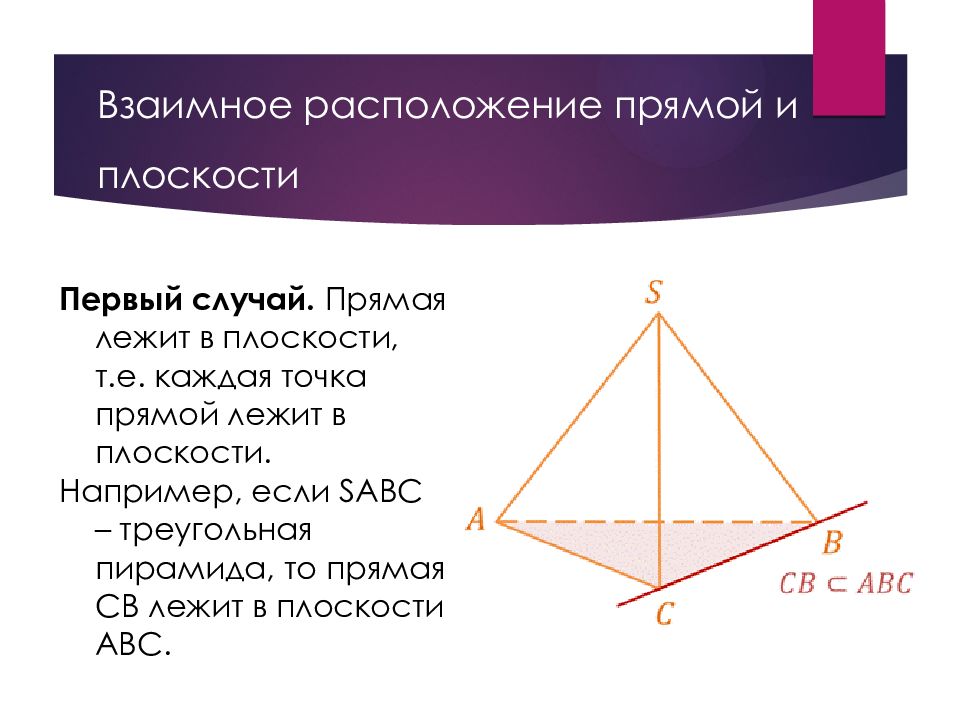
Слайд 5: Взаимное расположение прямой и плоскости
Первый случай. Прямая лежит в плоскости, т.е. каждая точка прямой лежит в плоскости. Например, если SABC – треугольная пирамида, то прямая CB лежит в плоскости ABC.
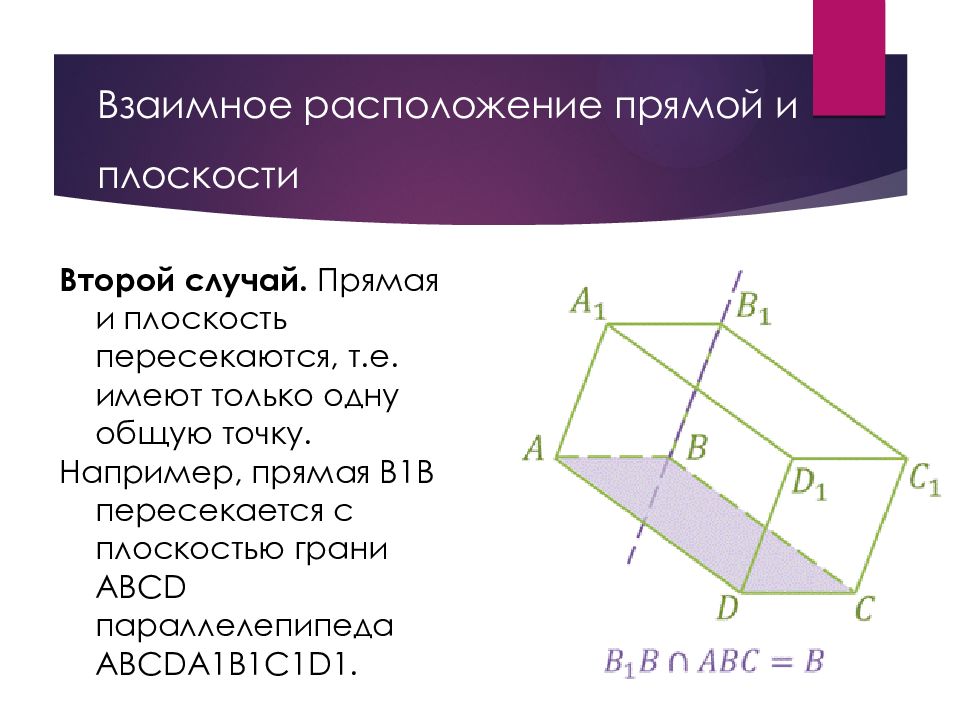
Слайд 6: Взаимное расположение прямой и плоскости
Второй случай. Прямая и плоскость пересекаются, т.е. имеют только одну общую точку. Например, прямая B1B пересекается с плоскостью грани ABCD параллелепипеда ABCDA1B1C1D1.
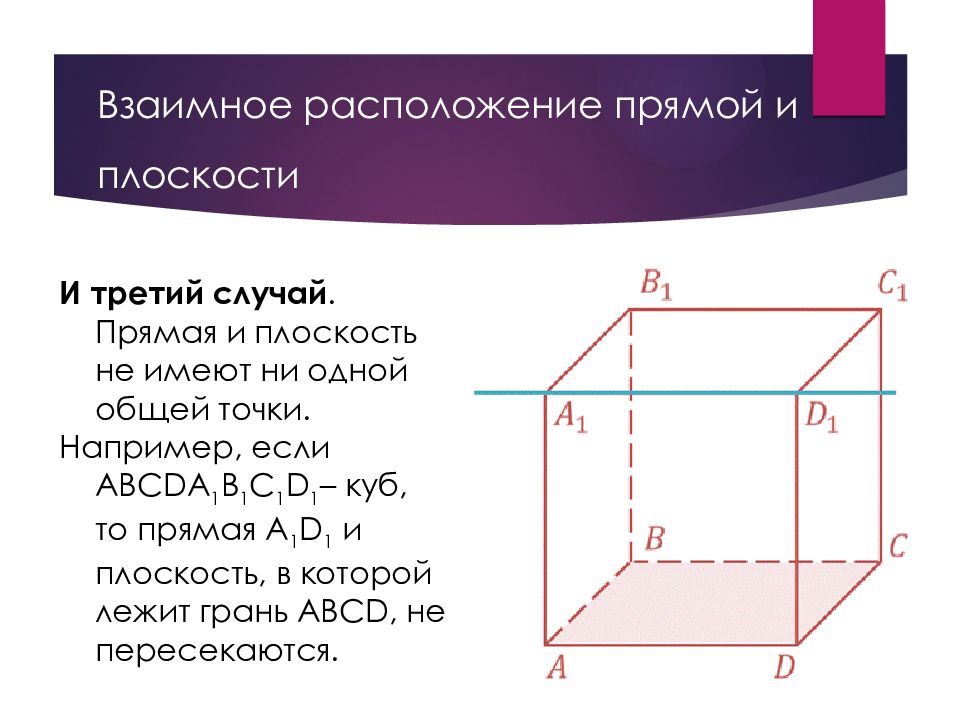
Слайд 7: Взаимное расположение прямой и плоскости
И третий случай. Прямая и плоскость не имеют ни одной общей точки. Например, если ABCDA 1 B 1 C 1 D 1 – куб, то прямая A 1 D 1 и плоскость, в которой лежит грань ABCD, не пересекаются.
Слайд 8: Параллельные прямая и плоскость
Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут :
Слайд 9: Параллельные прямая и плоскость
Теорема 1 (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
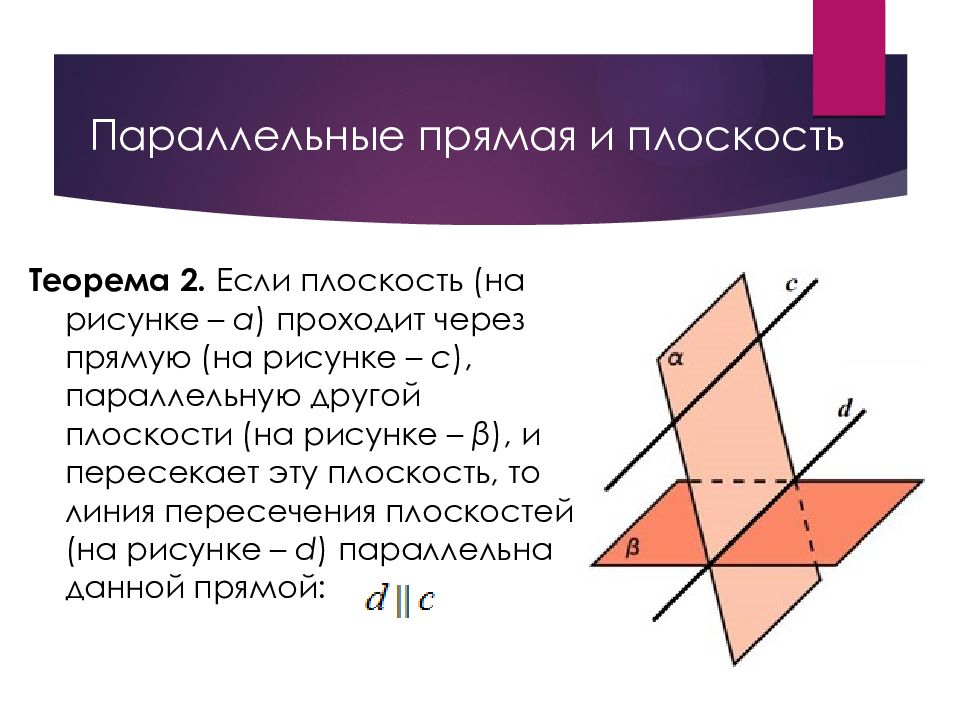
Слайд 10: Параллельные прямая и плоскость
Теорема 2. Если плоскость (на рисунке – α ) проходит через прямую (на рисунке – с ), параллельную другой плоскости (на рисунке – β ), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке – d ) параллельна данной прямой:
Слайд 13: Параллельные плоскости
Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:
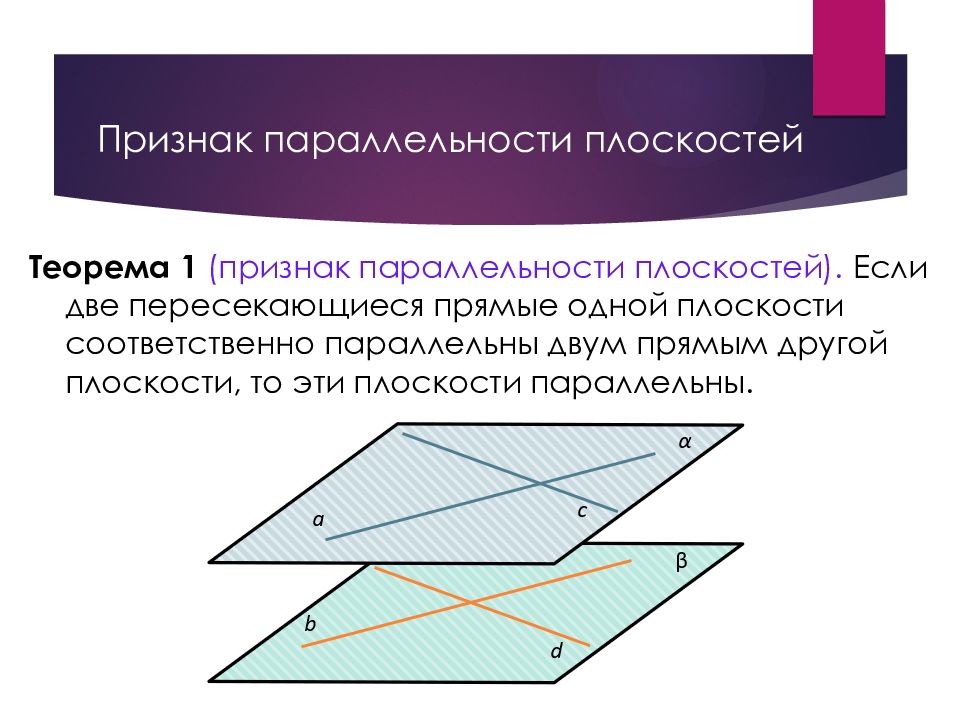
Слайд 14: Признак параллельности плоскостей
Теорема 1 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Слайд 15: Свойство противолежащих граней параллелепипеда
Теорема 2 (о свойстве противолежащих граней параллелепипеда). Противолежащие грани параллелепипеда лежат в параллельных плоскостях. Противолежащие грани – это те, которые не имеют общих точек.
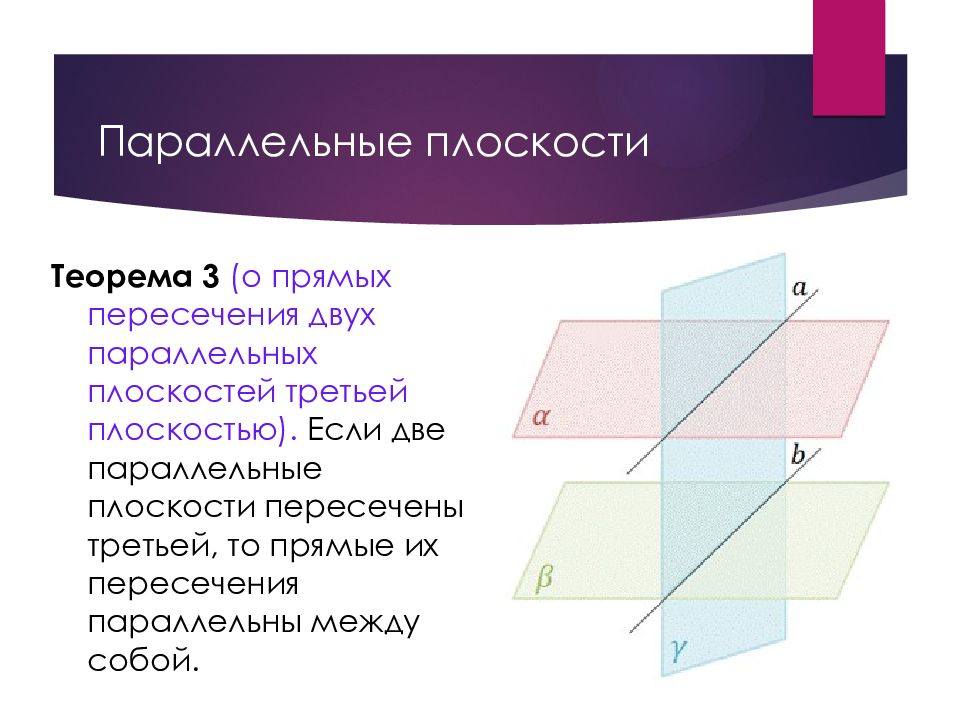
Слайд 16: Параллельные плоскости
Теорема 3 (о прямых пересечения двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.
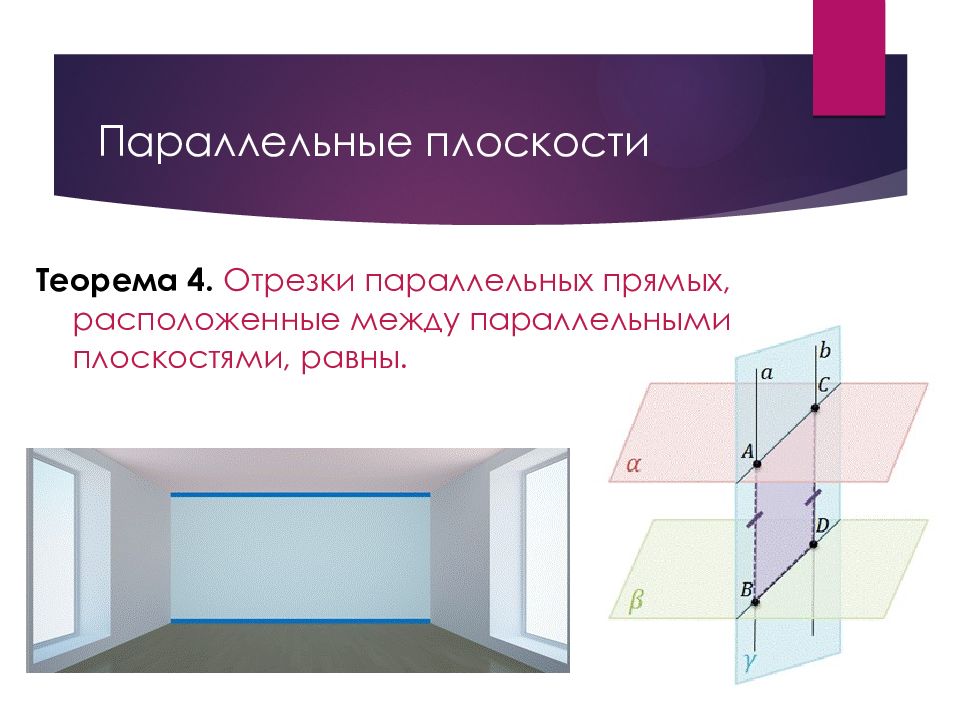
Слайд 17: Параллельные плоскости
Теорема 4. Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.
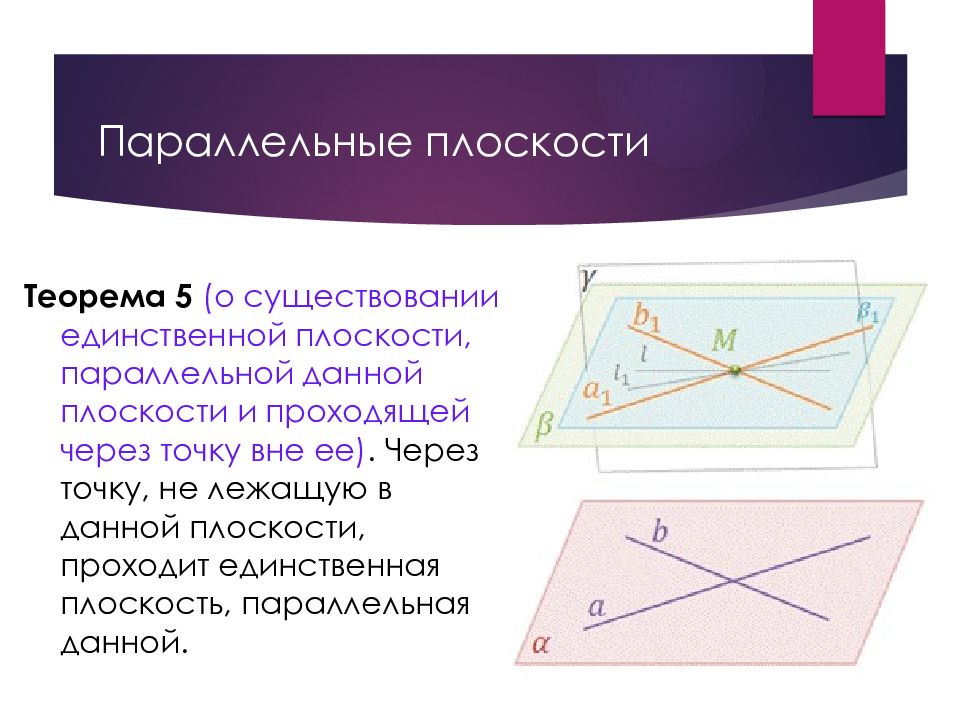
Слайд 18: Параллельные плоскости
Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее). Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.
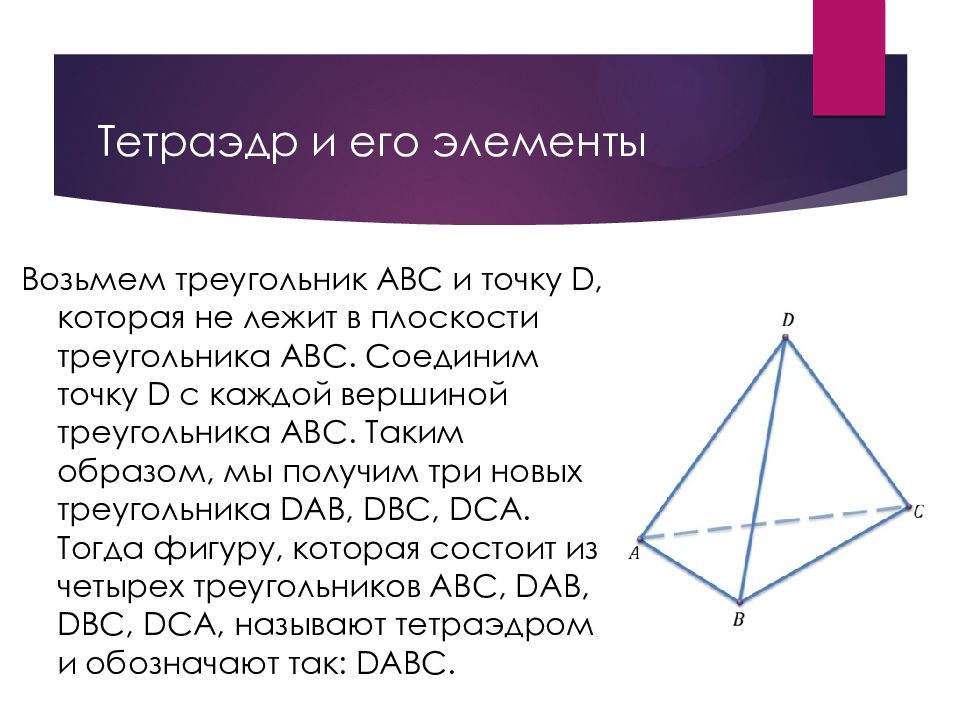
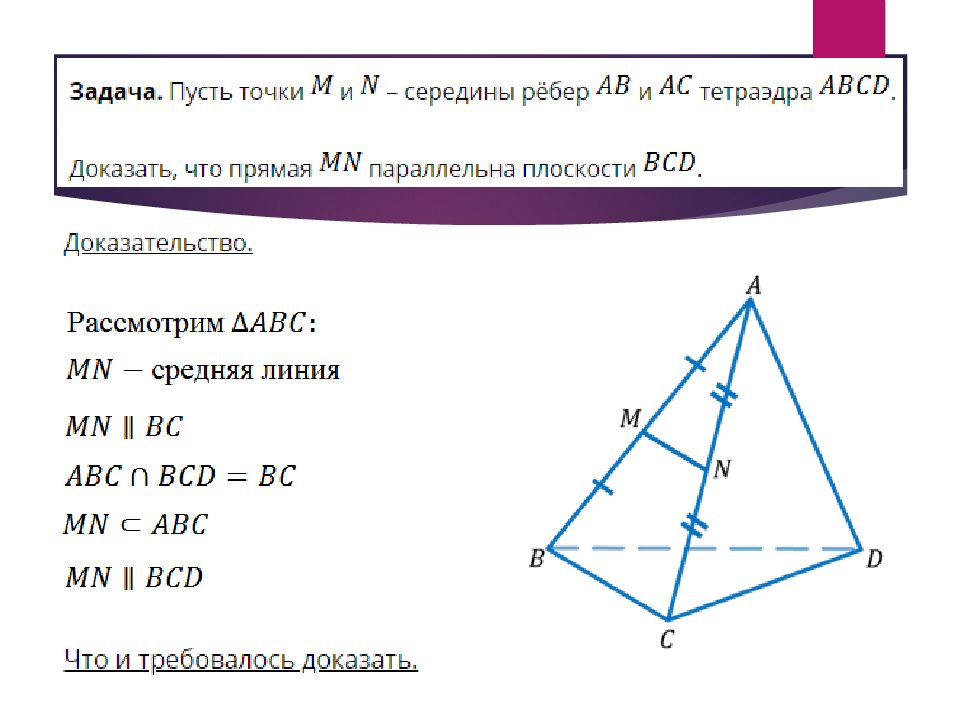
Слайд 21: Тетраэдр и его элементы
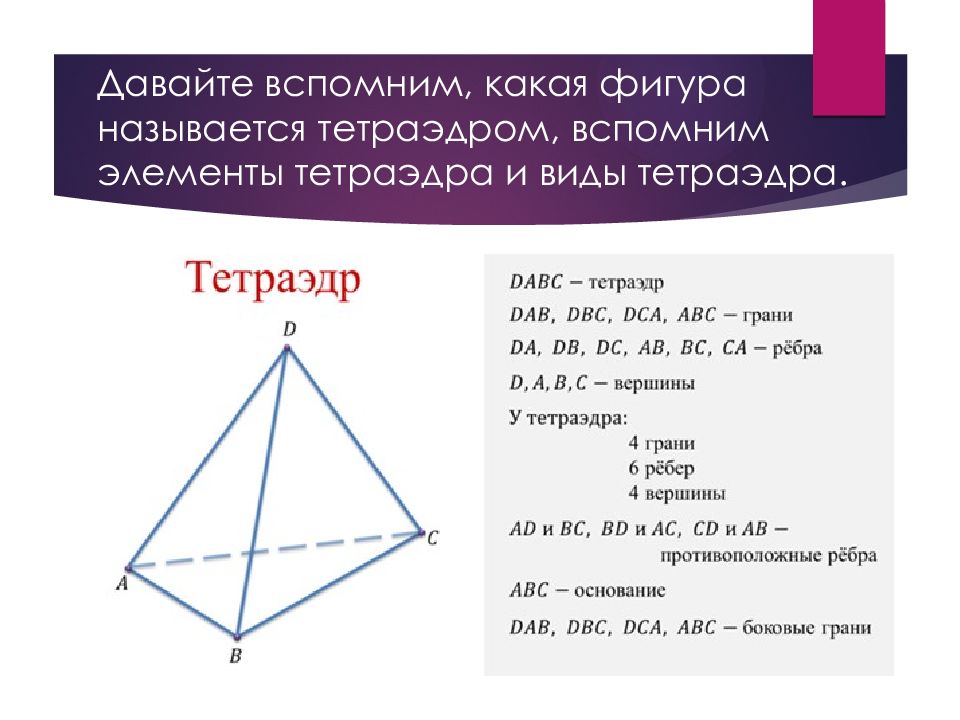
Возьмем треугольник ABC и точку D, которая не лежит в плоскости треугольника ABC. Соединим точку D с каждой вершиной треугольника ABC. Таким образом, мы получим три новых треугольника DAB, DBC, DCA. Тогда фигуру, которая состоит из четырех треугольников ABC, DAB, DBC, DCA, называют тетраэдром и обозначают так: DABC.
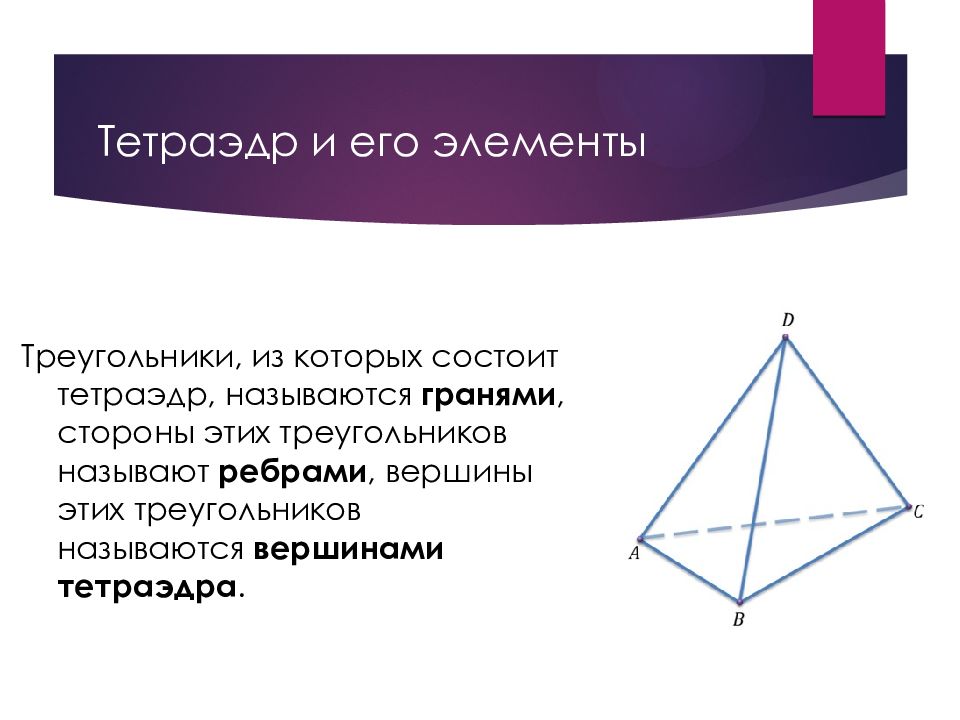
Слайд 22: Тетраэдр и его элементы
Треугольники, из которых состоит тетраэдр, называются гранями, стороны этих треугольников называют ребрами, вершины этих треугольников называются вершинами тетраэдра.
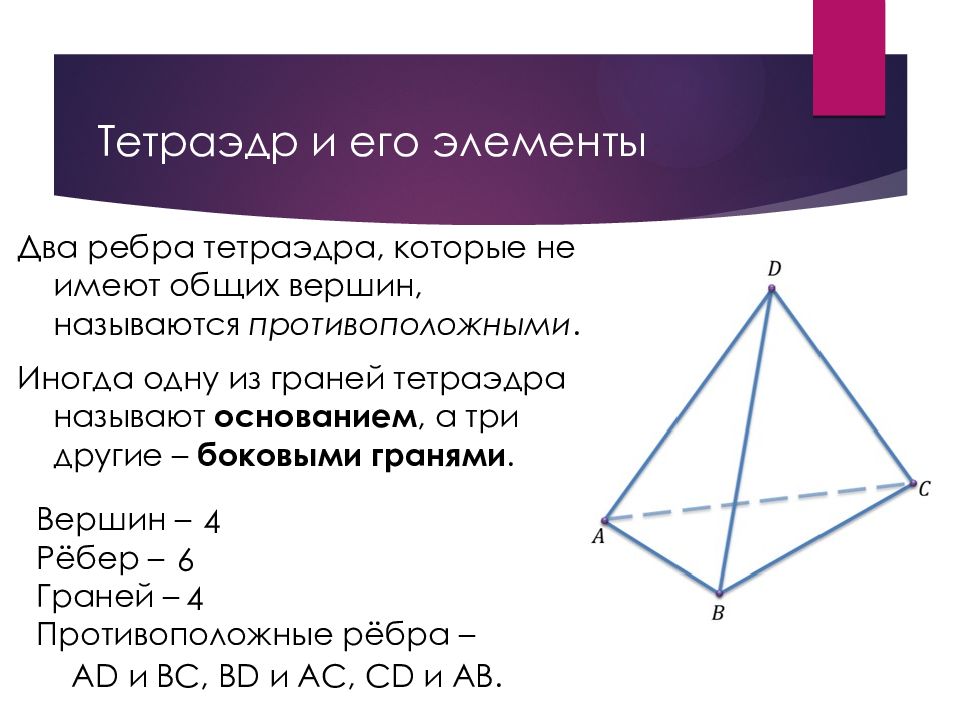
Слайд 23: Тетраэдр и его элементы
Два ребра тетраэдра, которые не имеют общих вершин, называются противоположными. Иногда одну из граней тетраэдра называют основанием, а три другие – боковыми гранями. Вершин – Рёбер – Граней – Противоположные рёбра – 4 6 4 AD и BC, BD и AC, CD и AB.
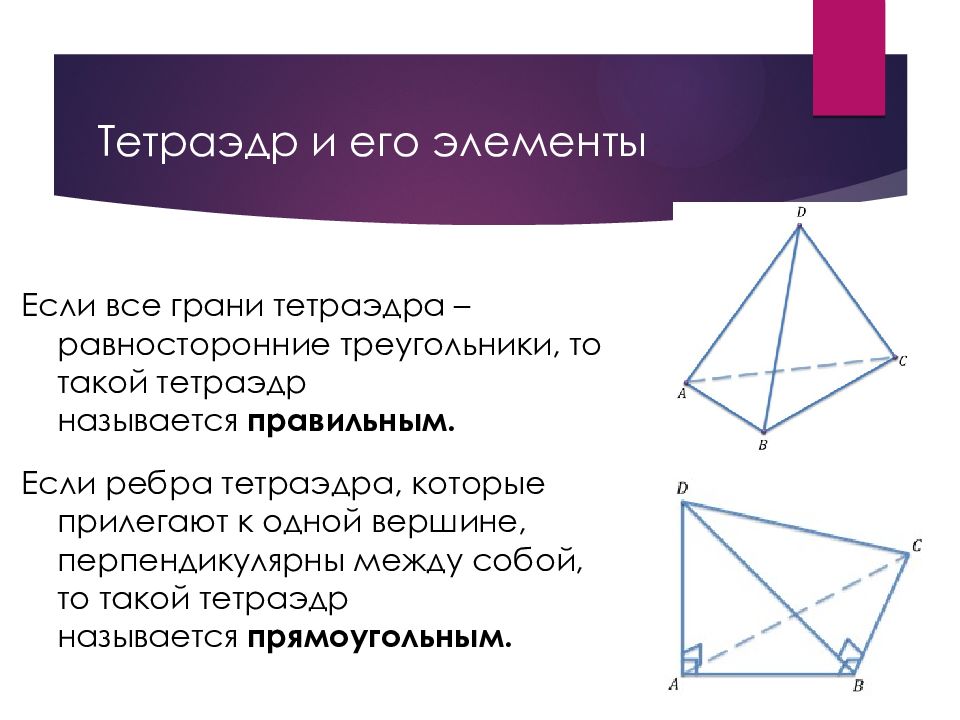
Слайд 24: Тетраэдр и его элементы
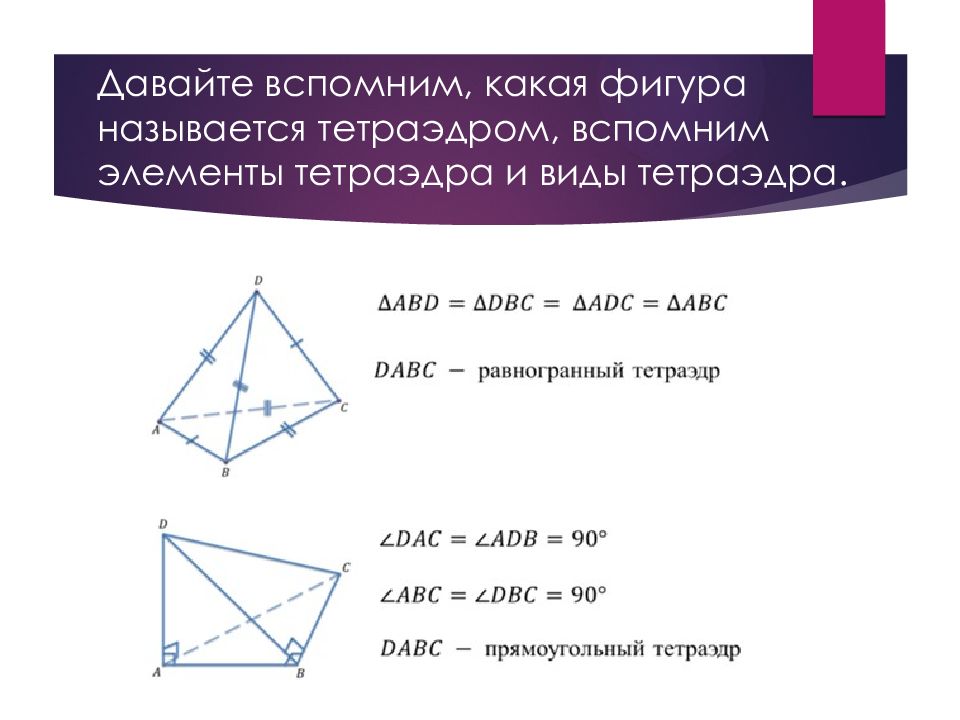
Если все грани тетраэдра – равносторонние треугольники, то такой тетраэдр называется правильным. Если ребра тетраэдра, которые прилегают к одной вершине, перпендикулярны между собой, то такой тетраэдр называется прямоугольным.
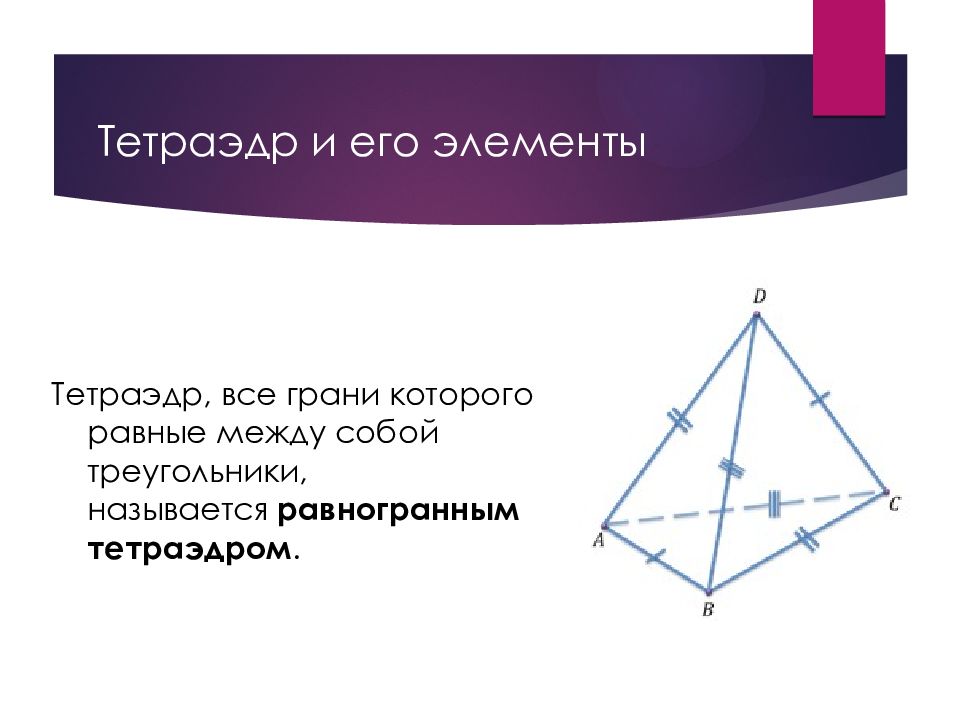
Слайд 25: Тетраэдр и его элементы
Тетраэдр, все грани которого равные между собой треугольники, называется равногранным тетраэдром.
Слайд 26: Тетраэдр и его элементы
Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов.
Слайд 27: Пример использования тетраэдра в строительных конструкциях
Ярким примером тетраэдра является разработанное для Нового Орлеана «здание-город», которое возвышается на 360 метров, включает в себя 20000 квартир, суммарная жилая площадь которых 2040000 квадратных метров. Здание использует экологичное энергоснабжение — энергию ветра, воды и солнца. Кроме квартир в тетраэдре помещаются коммерческие организации, три отеля, культурные объекты, школа, больницы и казино. И, учитывая место, под которое создавался проект, его немаловажная особенность — способность держаться на плаву.
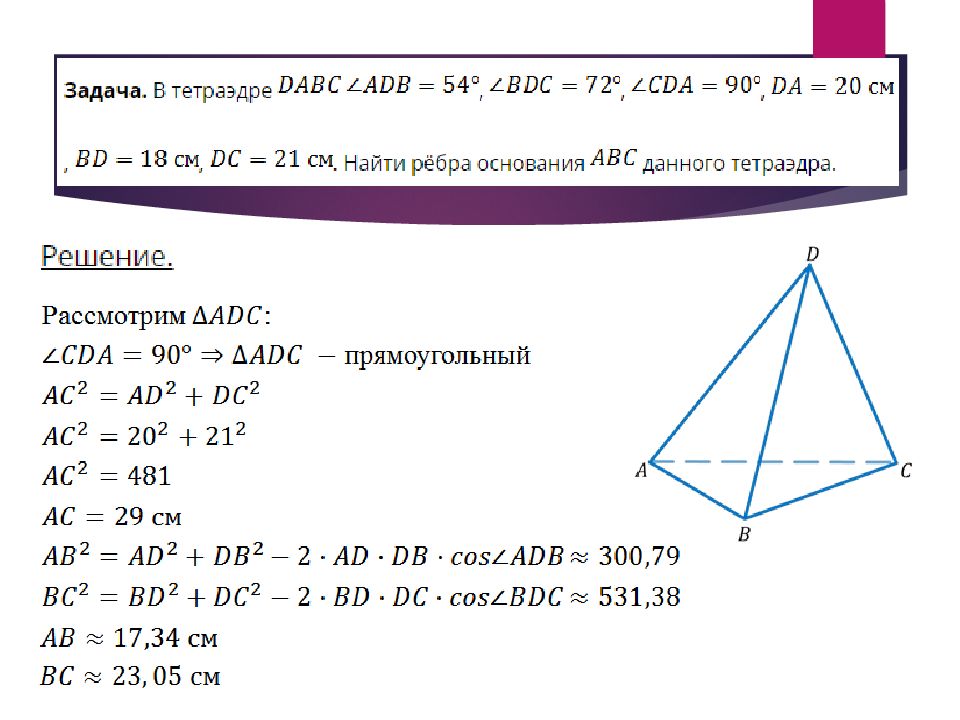
Слайд 29: Д авайте вспомним, какая фигура называется тетраэдром, вспомним элементы тетраэдра и виды тетраэдра
Слайд 30: Д авайте вспомним, какая фигура называется тетраэдром, вспомним элементы тетраэдра и виды тетраэдра
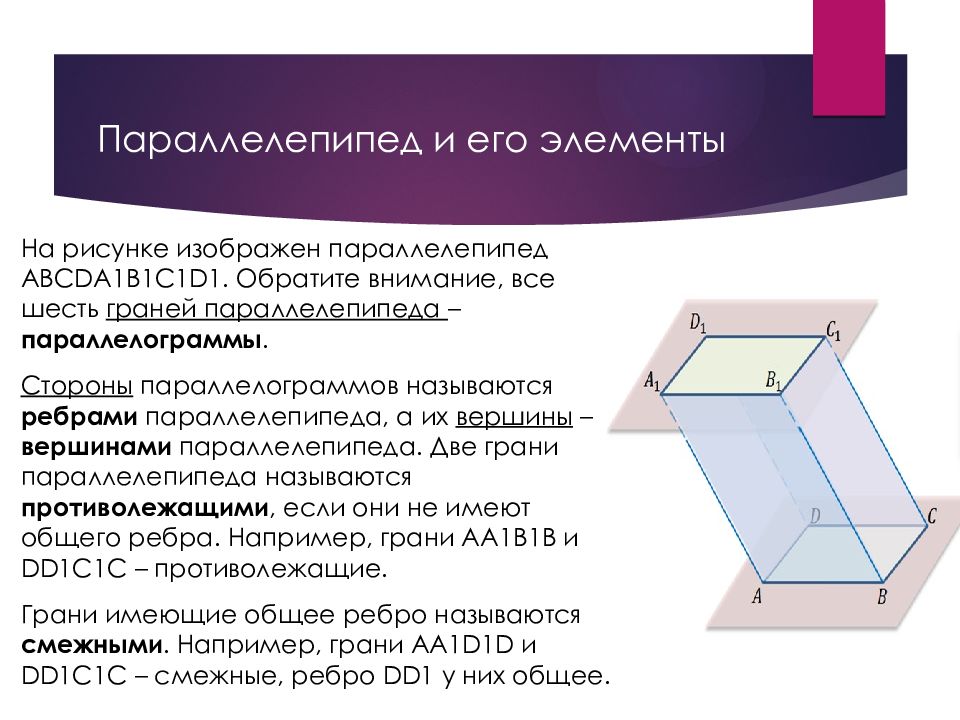
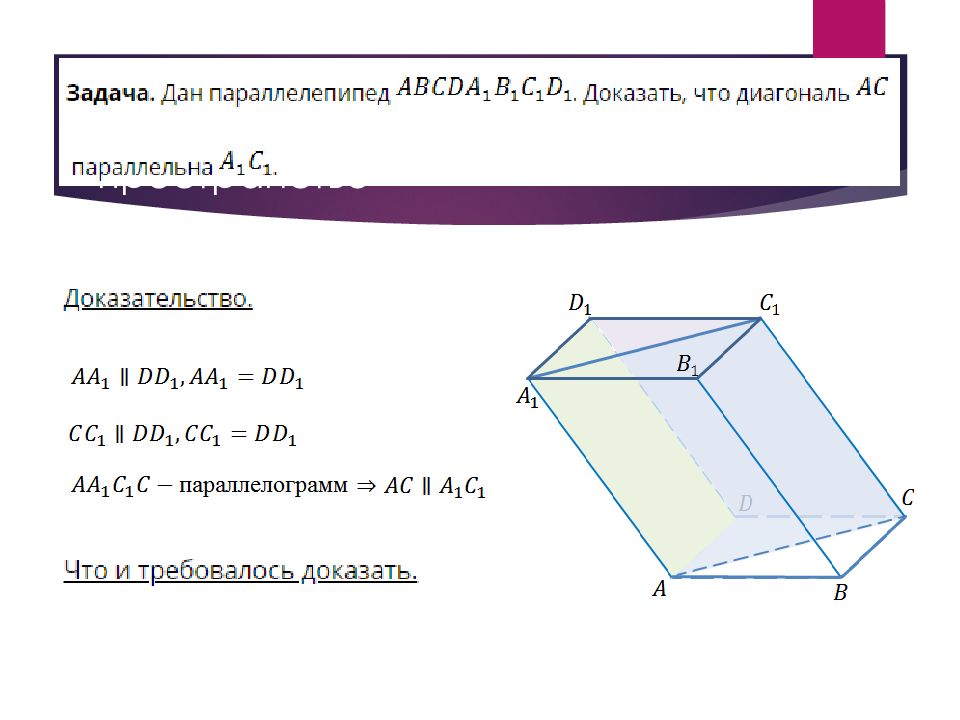
Слайд 35: Параллелепипед и его элементы
Рассмотрим два равных параллелограмма ABCD и A 1 B 1 C 1 D 1, которые расположены в параллельных плоскостях так, что отрезки AA 1, BB 1, CC 1, DD 1 параллельны. Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов ABB1A1, BCC1B1, CDD1C1, DAA1D1называется параллелепипедом и обозначается так: ABCDA1B1C1D1 Параллелограммы, из которых составлен параллелепипед, называются гранями.
Слайд 36: Параллелепипед и его элементы
На рисунке изображен параллелепипед ABCDA1B1C1D1. Обратите внимание, все шесть граней параллелепипеда – параллелограммы. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра. Например, грани AA1B1B и DD1C1C – противолежащие. Грани имеющие общее ребро называются смежными. Например, грани AA1D1D и DD1C1C – смежные, ребро DD1 у них общее.
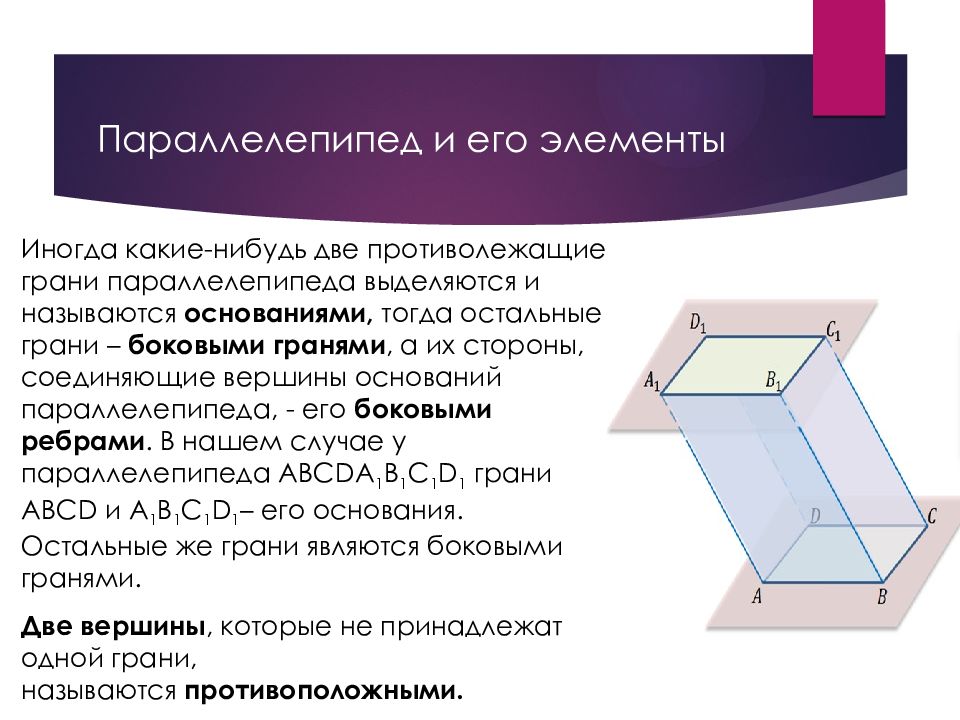
Слайд 37: Параллелепипед и его элементы
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, - его боковыми ребрами. В нашем случае у параллелепипеда ABCDA 1 B 1 C 1 D 1 грани ABCD и A 1 B 1 C 1 D 1 – его основания. Остальные же грани являются боковыми гранями. Две вершины, которые не принадлежат одной грани, называются противоположными.
Слайд 38: Параллелепипед и его элементы
Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, - его боковыми ребрами. В нашем случае у параллелепипеда ABCDA 1 B 1 C 1 D 1 грани ABCD и A 1 B 1 C 1 D 1 – его основания. Остальные же грани являются боковыми гранями. Две вершины, которые не принадлежат одной грани, называются противоположными.
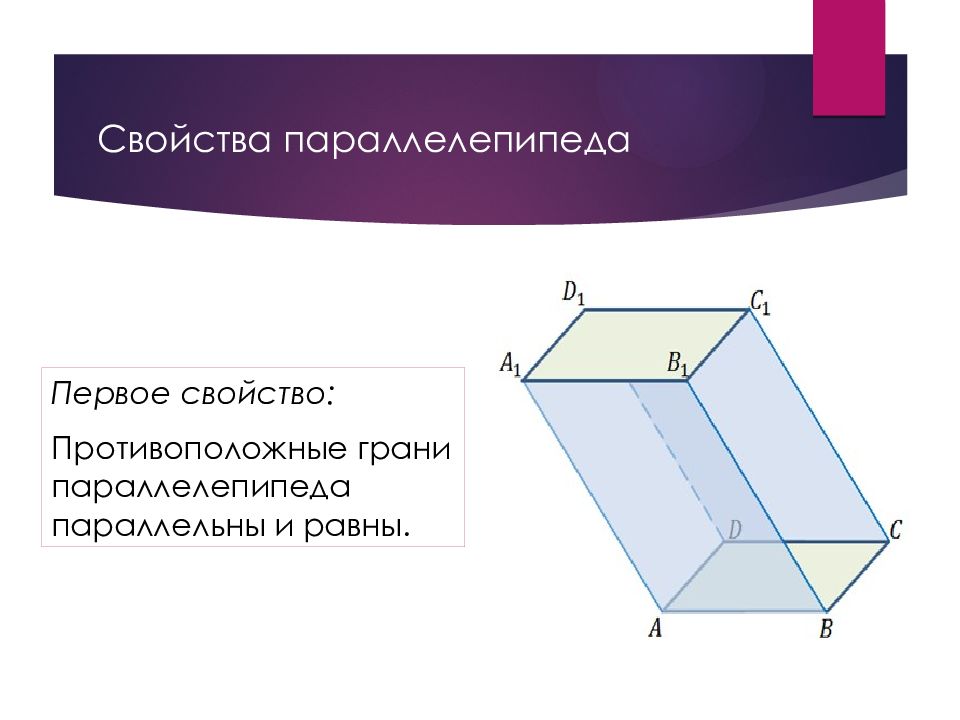
Слайд 39: Свойства параллелепипеда
Первое свойство: Противоположные грани параллелепипеда параллельны и равны.
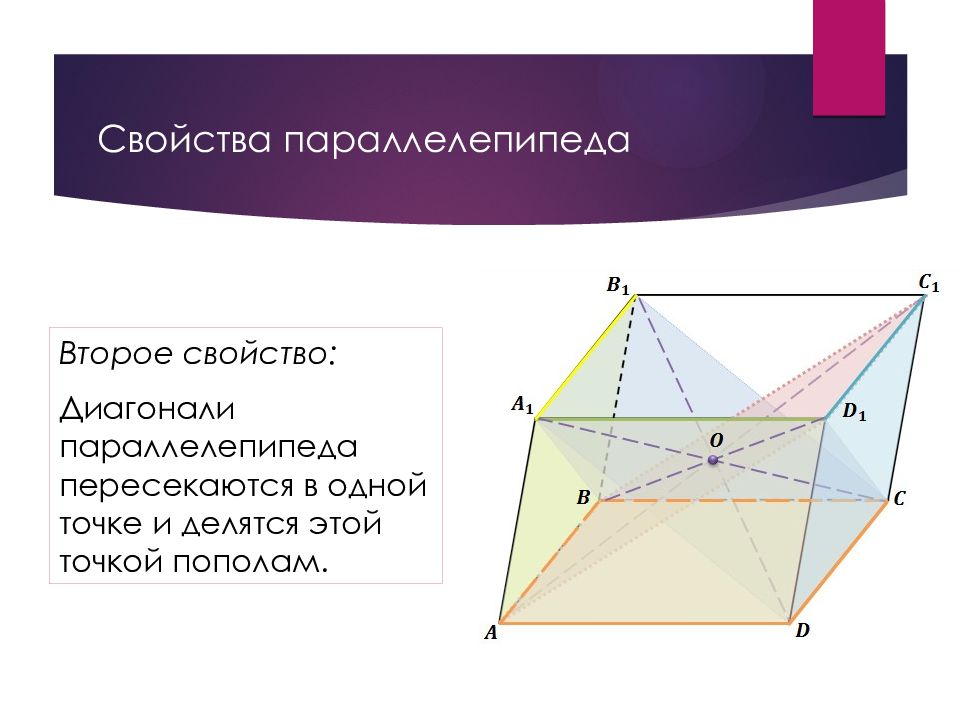
Слайд 40: Свойства параллелепипеда
Второе свойство: Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
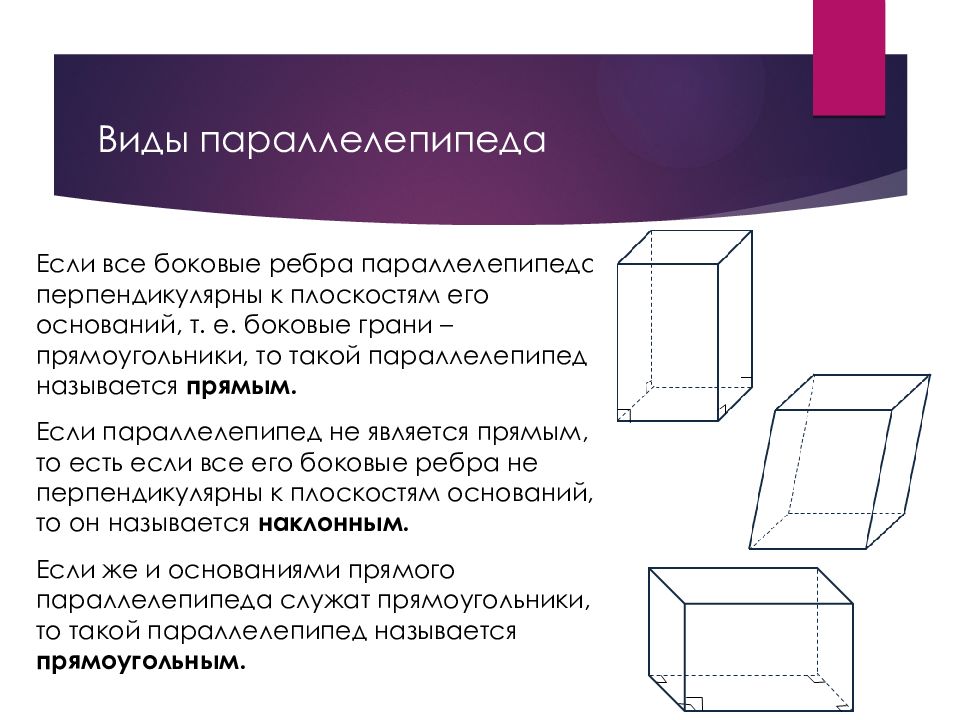
Слайд 41: Виды параллелепипеда
Если все боковые ребра параллелепипеда перпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такой параллелепипед называется прямым. Если параллелепипед не является прямым, то есть если все его боковые ребра не перпендикулярны к плоскостям оснований, то он называется наклонным. Если же и основаниями прямого параллелепипеда служат прямоугольники, то такой параллелепипед называется прямоугольным.
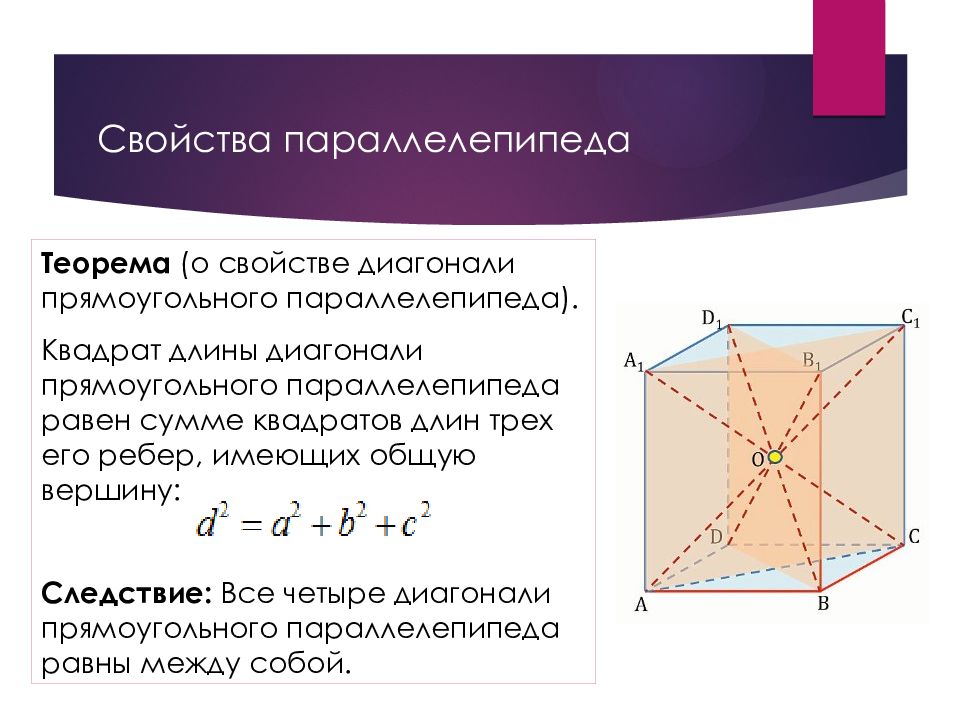
Слайд 42: Свойства параллелепипеда
Теорема (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину : Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.
Слайд 47: Основные определения
Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба). Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости.
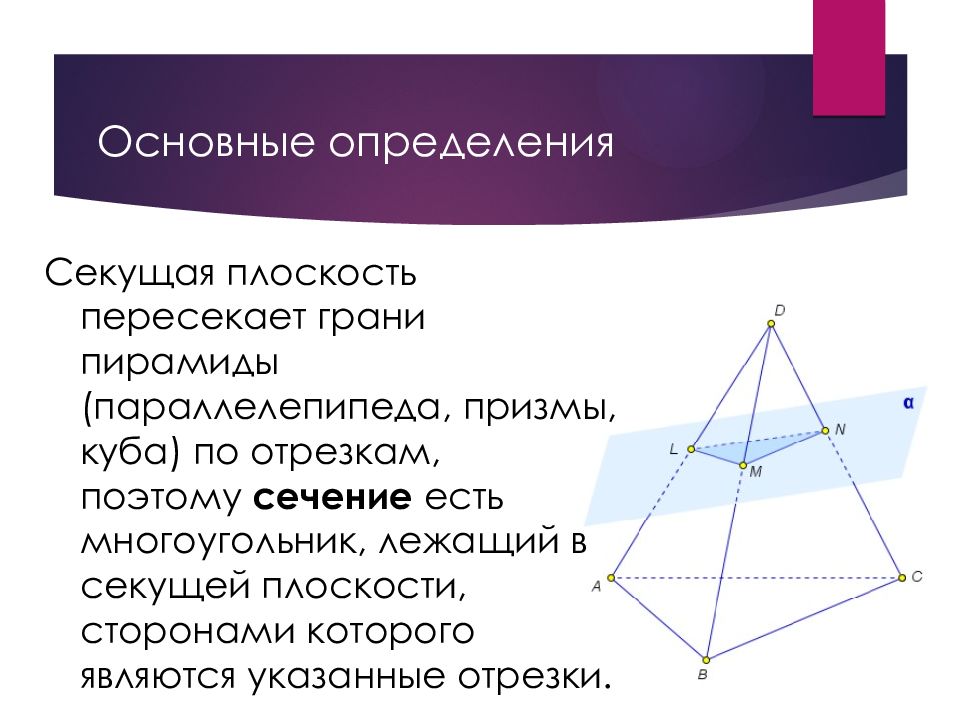
Слайд 48: Основные определения
Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтому сечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.
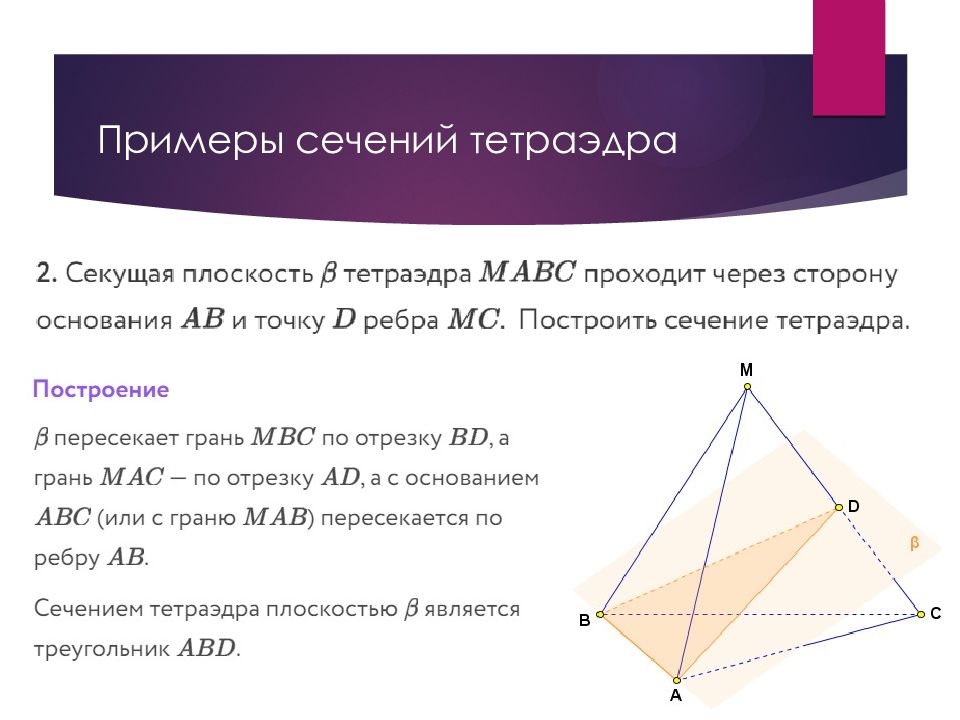
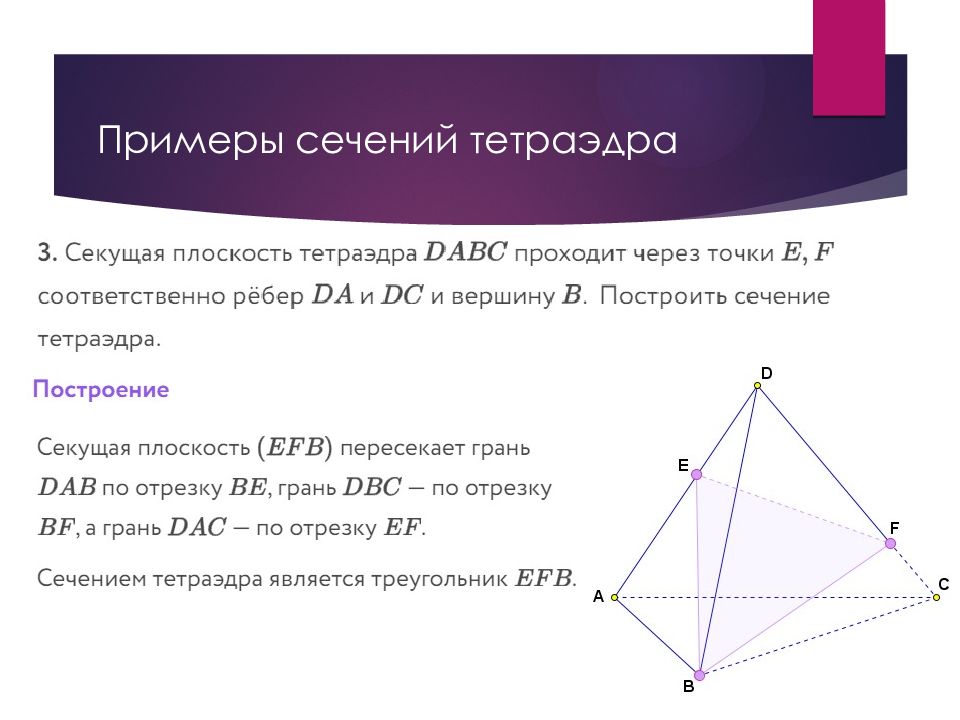
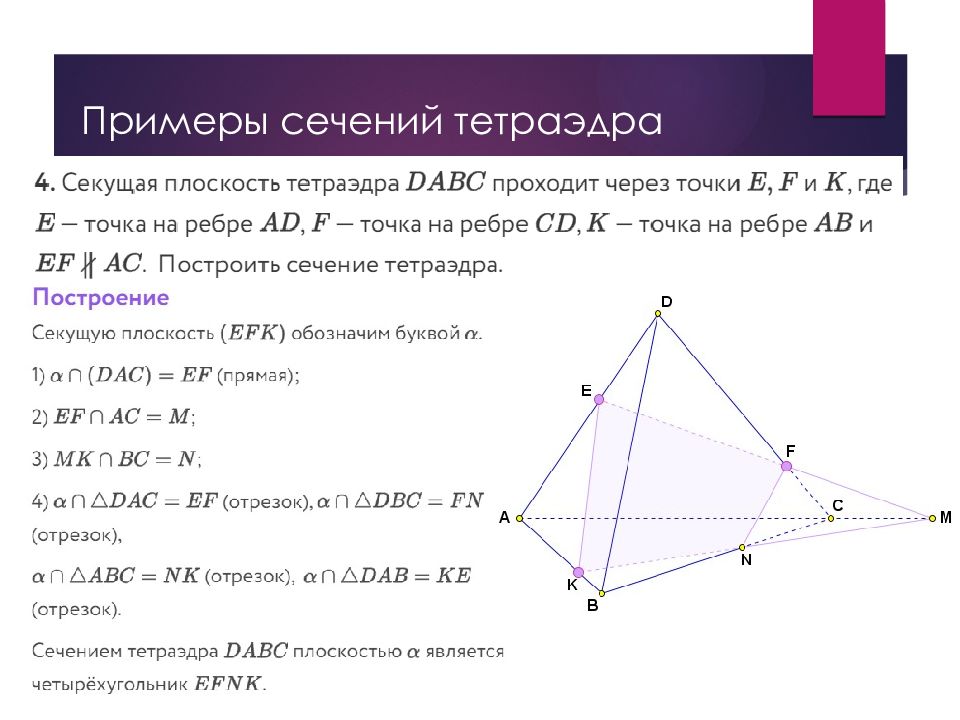
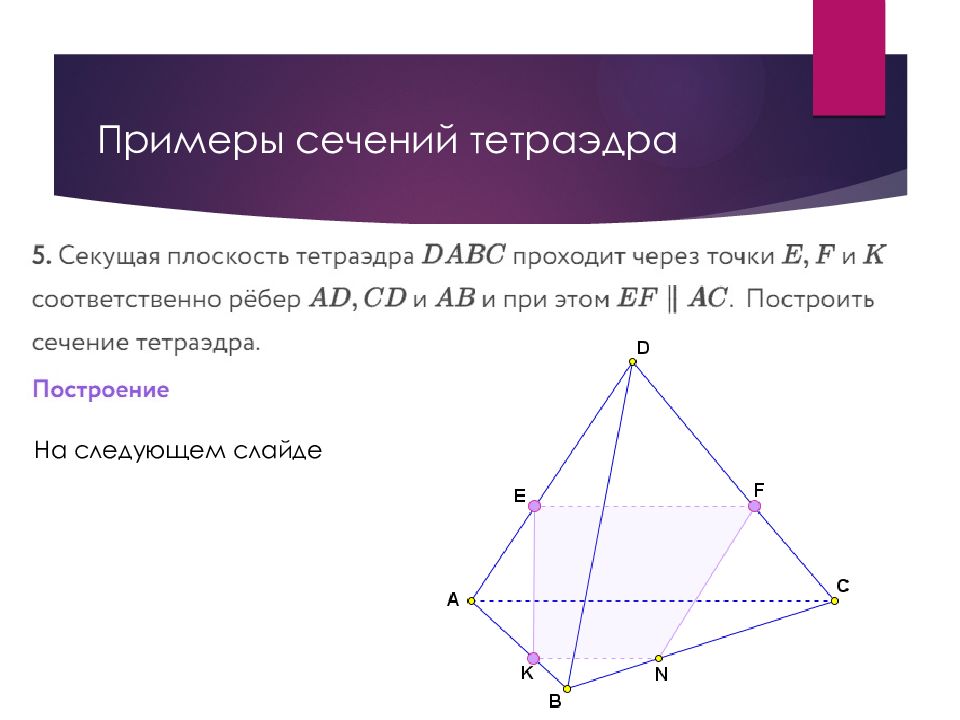
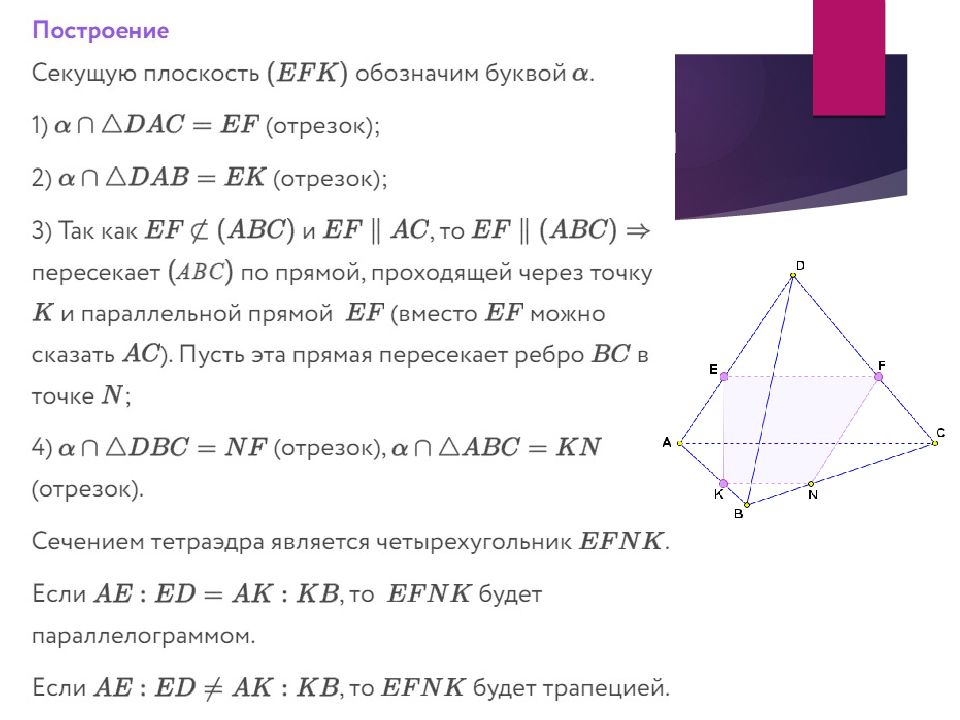
Слайд 49: Построение сечений в стереометрии
Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна.
Слайд 50: Построение сечений в стереометрии
В основе построения сечений многогранников лежит две задачи на построение: Линии пересечения двух плоскостей. Для построения прямой, по которой пересекаются некоторые две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β. Точки пересечения прямой и плоскости. Для построения точки пересечения прямой l и плоскости α нужно построить точку пересечения прямой l и прямой l 1, по которой пересекаются плоскость α и любая плоскость, содержащая прямую l. Построение сечений в стереометрии
Слайд 51: Построение сечений в стереометрии
Правила построения сечений многогранников: 1) проводим прямые через точки, лежащие в одной плоскости; 2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости); б) параллельные грани плоскость сечения пересекает по параллельным прямым. Построение сечений в стереометрии
Слайд 58: Примеры сечений параллелепипеда
Больше подробных примеров построения сечений тут: https ://uztest.ru/abstracts/?idabstract=511902
Слайд 60: Домашняя работа (обязательно к выполнению )
Дополнить конспект в тетради со всей этой презентации. Решить задачи: