Слайд 2: Логика, высказывания
2 Логика, высказывания Аристотель (384-322 до н.э.) Логика (др.греч. λογικ ο ς ) – это наука о том, как правильно рассуждать, делать выводы, доказывать утверждения. Формальная логика отвлекается от конкретного содержания, изучает только истинность и ложность высказываний. Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.
Слайд 3: Высказывание или нет?
3 Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата – 10 сторон и все разные. Красиво! В городе N живут 2 миллиона человек. Который час?
Слайд 4: Логика и компьютер
4 Логика и компьютер Логика изучает операции между 0 и 1! Джордж Буль Алгебра логики — это математический аппарат, с помощью которого записывают, упрощают и преобразуют логические высказывания, вычисляют их значения. Связь с двоичным кодированием! ! Алгебра высказываний, булева алгебра Любое высказывание может быть ложно ( 0 ) или истинно ( 1 ). ! двоичная логика
Слайд 5: Простые и составные высказывания
5 Простые и составные высказывания A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания строятся из простых с помощью логических связок (операций) « и», « или», « не», « если … то», « тогда и только тогда» и др. A и B A или не B если A, то B A тогда и только тогда, когда B Сейчас идет дождь и открыта форточка. Сейчас идет дождь или форточка закрыта. Если сейчас идет дождь, то форточка открыта. Дождь идет тогда и только тогда, когда открыта форточка.
Слайд 6: Операция НЕ ( инверсия)
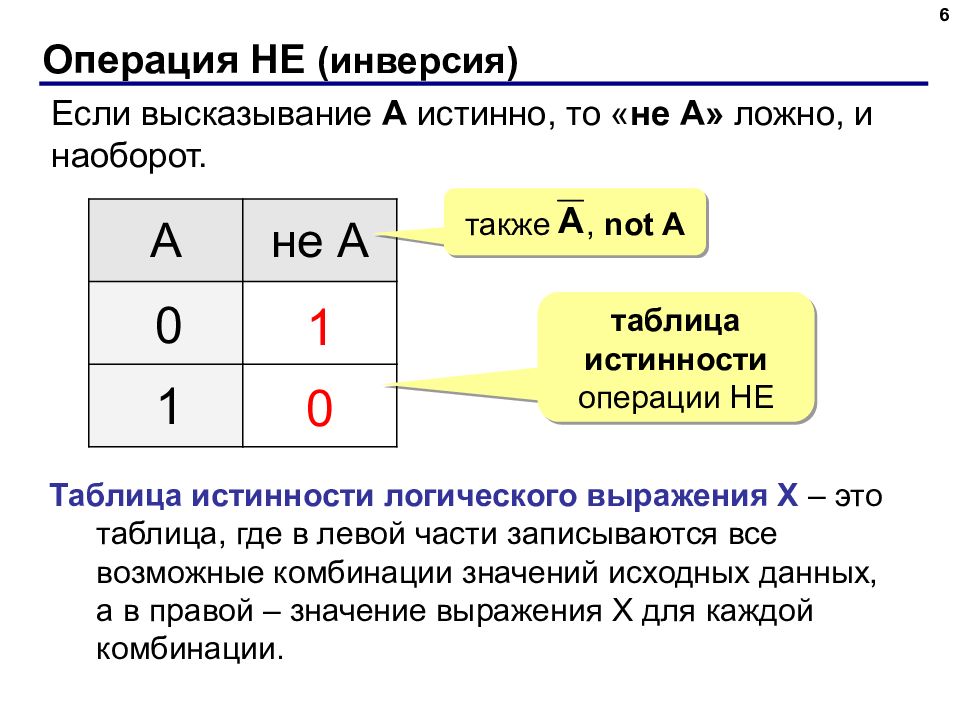
6 Операция НЕ ( инверсия) Если высказывание A истинно, то « не А» ложно, и наоборот. А не А 1 0 0 1 таблица истинности операции НЕ Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации. также, not A
Слайд 7: Операция И
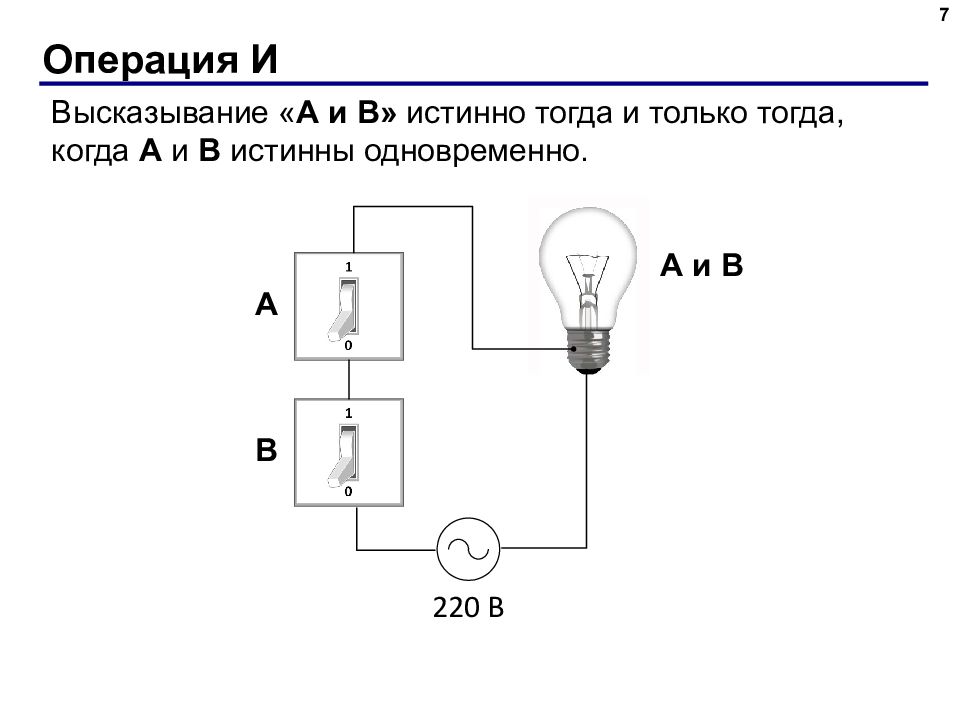
7 Операция И Высказывание « A и B » истинно тогда и только тогда, когда А и B истинны одновременно. 220 В A и B A B
Слайд 8: Операция И ( логическое умножение, конъюнкция)
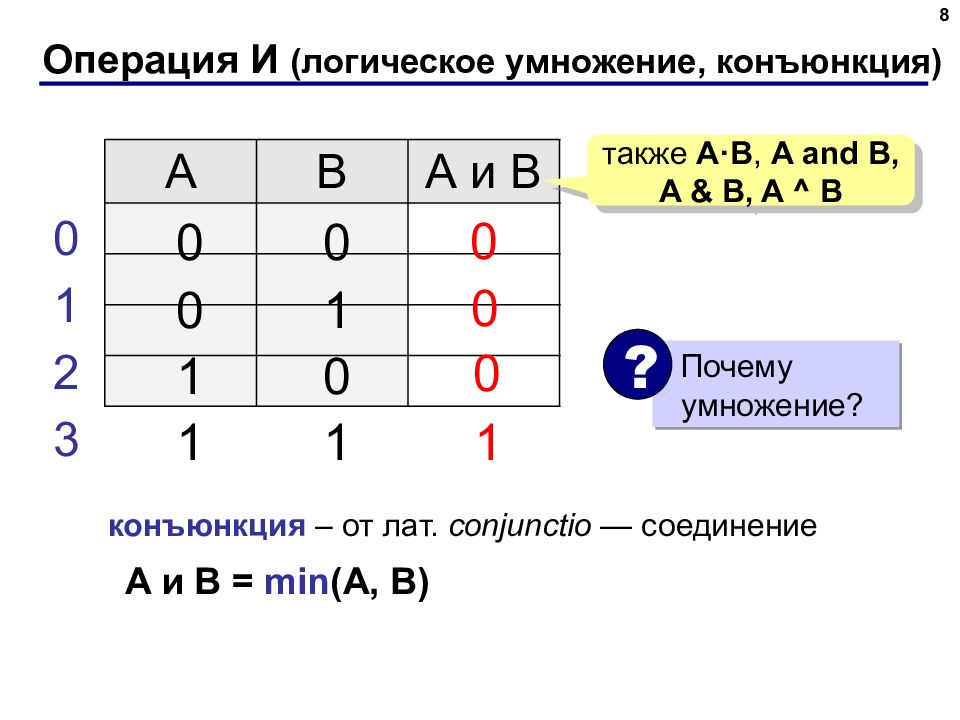
8 Операция И ( логическое умножение, конъюнкция) A B А и B 1 0 также A·B, A and B, A & B, A ^ B 0 0 0 1 1 0 1 1 0 1 2 3 0 0 конъюнкция – от лат. conjunctio — соединение Почему умножение? ? A и B = min (A, B)
Слайд 9: Операция ИЛИ ( логическое сложение, дизъюнкция)
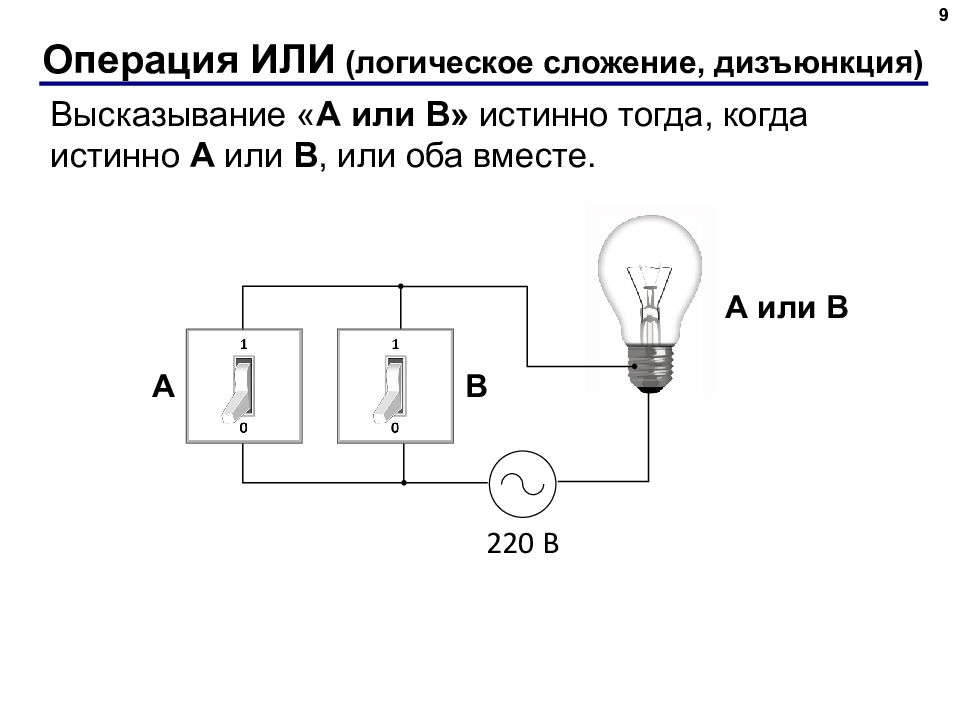
9 Операция ИЛИ ( логическое сложение, дизъюнкция) Высказывание « A или B » истинно тогда, когда истинно А или B, или оба вместе. 220 В A или B A B
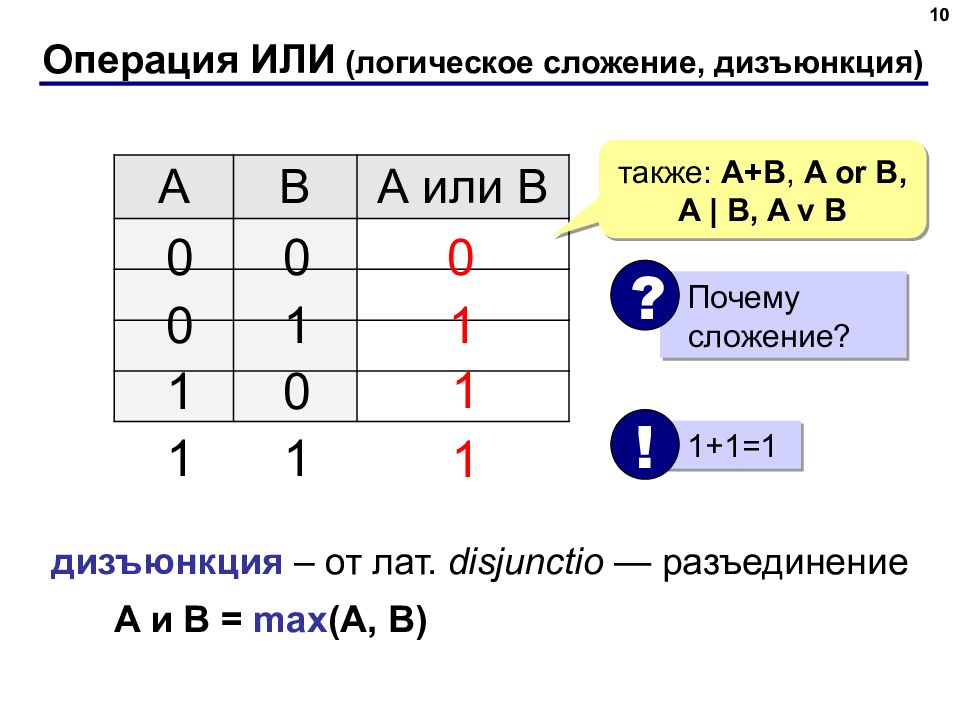
Слайд 10: Операция ИЛИ ( логическое сложение, дизъюнкция)
10 Операция ИЛИ ( логическое сложение, дизъюнкция) A B А или B 1 0 также: A + B, A or B, A | B, A v B 0 0 0 1 1 0 1 1 1 1 дизъюнкция – от лат. dis junctio — разъединение A и B = max (A, B) Почему сложение? ? 1+1=1 !
Слайд 11: Логические выражения
11 Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь). Авария = вышли из строя 2 из 3-х двигателей. A – «Двигатель № 1 неисправен». B – «Двигатель № 2 неисправен». C – «Двигатель № 3 неисправен». Аварийный сигнал : X = «Неисправны два двигателя» = ( A и B) или ( A и C ) или ( B и C ) логическое выражение Формализация – это переход к записи на формальном языке! !
Слайд 12: Порядок вычисления
12 скобки НЕ И ИЛИ импликация эквиваленция 1 2 3 4 5 6 , исключающее ИЛИ
Слайд 13: Составление условий
13 0 1 2 3 4 5 6 7 8 ( x 3) и ( x 6) ( 3 x ) и ( x 6) 0 1 2 3 4 5 6 7 8 ( 1 x ) и ( x 3 ) или ( 5 x ) и ( x 8 ) 0 1 2 3 4 5 6 7 8
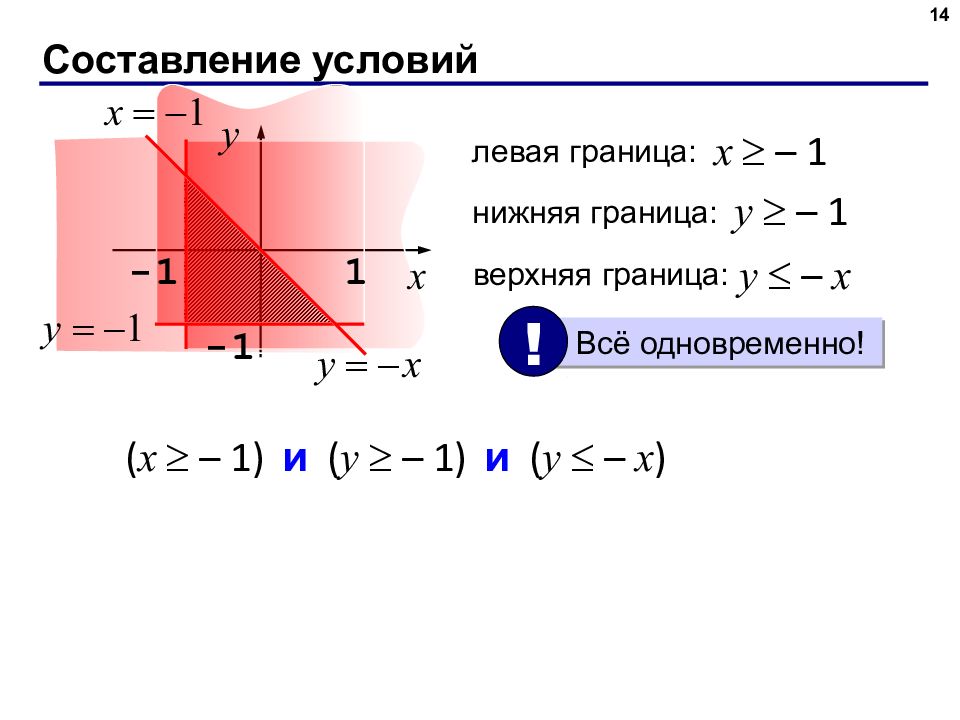
Слайд 14: Составление условий
14 левая граница: x – 1 нижняя граница: y – 1 верхняя граница: y – x Всё одновременно! ! ( x – 1) и ( y – 1) и ( y – x )
Слайд 15: Составление условий
15 ( x 2 +y 2 1) и ( x 0 ) левая правая ( x 0 ) и ( x 2 +y 2 1) левая нижняя и ( y – x ) верхняя
Слайд 16: Составление условий
16 = + ( … ) или ( … ) ( ( x 2 +y 2 1) и ( x 0 ) ) или ( ( x 2 +y 2 1) и ( x 0 ) и ( y – x ) ) Как упростить? ? ( x 2 +y 2 1) и ( ( x 0) или (( x 0 ) и ( y – x )) ) А ещё? ? ( x 2 +y 2 1) и ( ( x 0) или ( y – x ) )
Слайд 17: Определение истинности выражений
17 Для каких из указанных значений числа X истинно высказывание: (X < 5 ) И НЕ (X < 1 ) ? X = 2 : ( 1 ) И НЕ ( 0 ) X = 4 : ( 1 ) И НЕ ( 0 ) X = 8 : ( 0 ) И НЕ ( 0 ) ( 0 И 1) = 0 ( 1 И 1 ) = 1 ( 1 И 1 ) = 1 можно не вычислять!
Слайд 18: Задачи
18 Для каких из указанных значений числа X ЛОЖНО высказывание: (НЕ (X ≥ 3) И НЕ (X = 8)) ИЛИ ( X ≤ 5 ) ? X = 4: (НЕ ( 1 ) И НЕ ( 0 )) ИЛИ ( 1 ) = 1 X = 1: (НЕ ( 0 ) И НЕ ( 0 )) ИЛИ ( 1 ) = 1 X = 8 : (НЕ (1) И НЕ (1)) ИЛИ (0) ( 0 И 0 ) ИЛИ (0) = 0 ? + 1
Слайд 19: Задачи
19 Для каких значений числа X истинно высказывание: (X < 5 ) И НЕ (X < 1 ) ? (X < 5 ) И (X >= 1 ) 1 5 3 2 4 1, 2, 3, 4
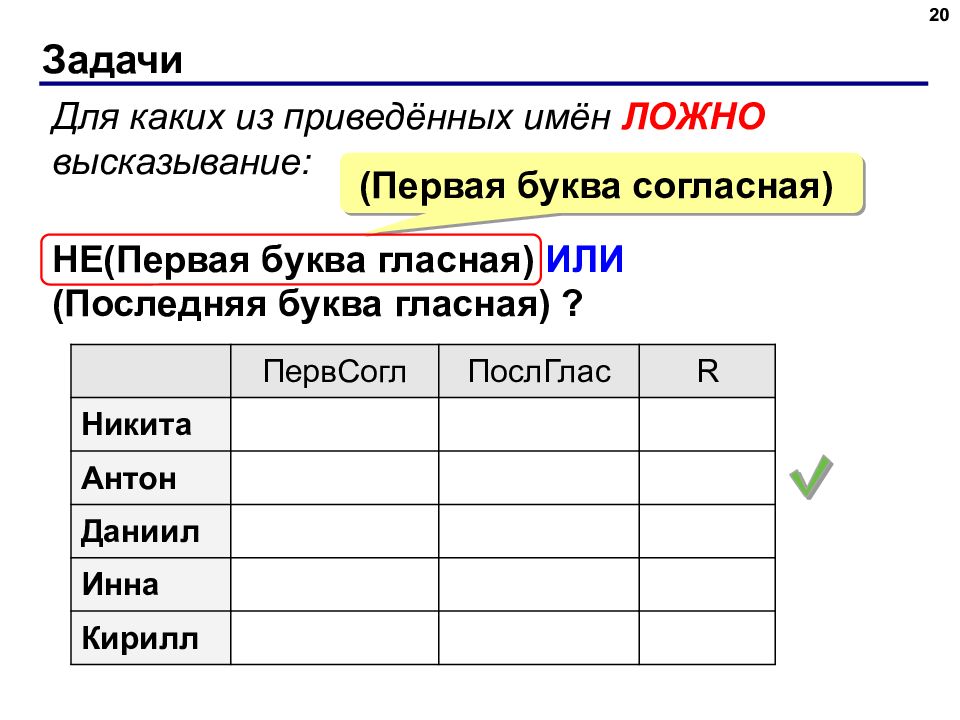
Слайд 20: Задачи
20 Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) ИЛИ (Последняя буква гласная) ? (Первая буква согласная) ПервСогл ПослГлас R Никита 1 1 1 Антон 0 0 0 Даниил 1 0 1 Инна 0 1 1 Кирилл 1 0 1
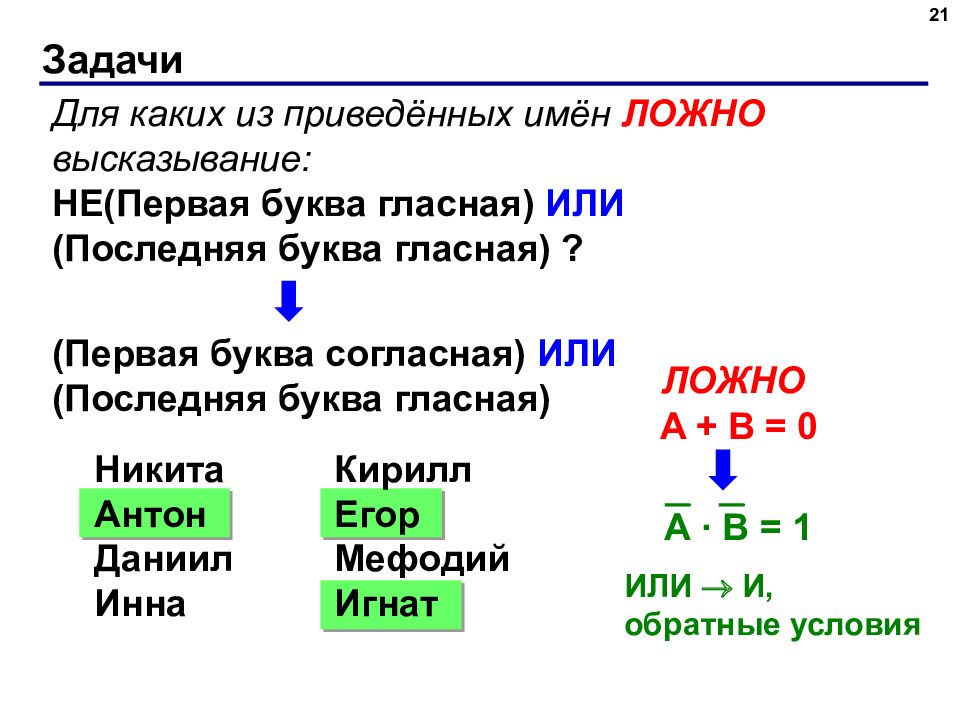
Слайд 21: Задачи
21 Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) ИЛИ (Последняя буква гласная) ? (Первая буква согласная) ИЛИ (Последняя буква гласная) Никита Антон Даниил Инна Кирилл Егор Мефодий Игнат ЛОЖНО A + B = 0 A · B = 1 ИЛИ И, обратные условия
Слайд 22: Задачи
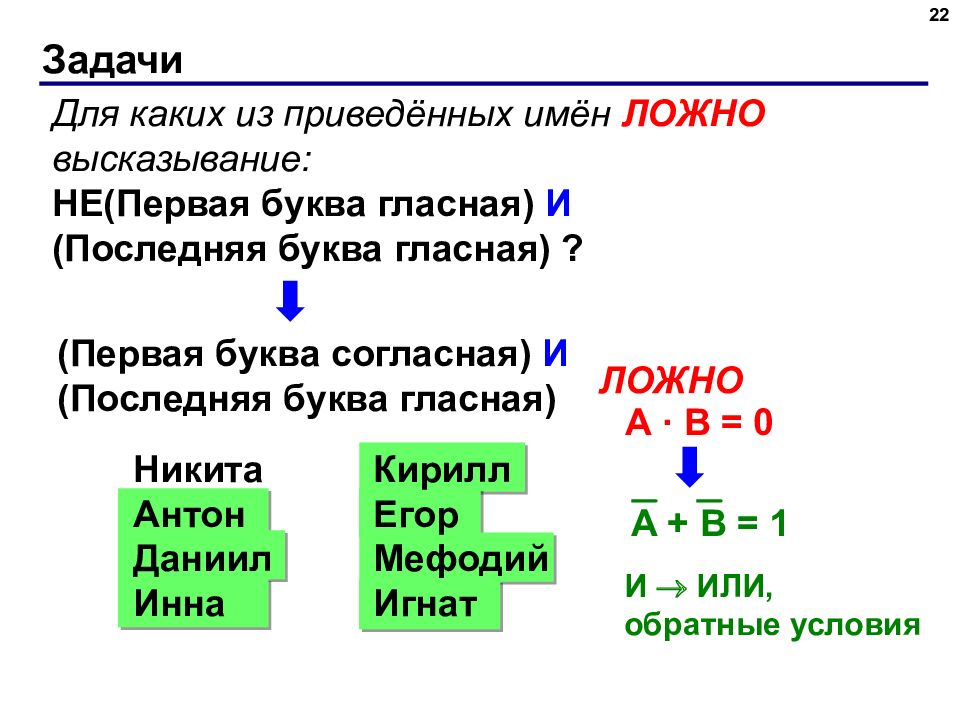
22 Для каких из приведённых имён ЛОЖНО высказывание: НЕ(Первая буква гласная) И (Последняя буква гласная) ? (Первая буква согласная) И (Последняя буква гласная) Никита Антон Даниил Инна Кирилл Егор Мефодий Игнат ЛОЖНО A · B = 0 A + B = 1 И ИЛИ, обратные условия
Слайд 23: Задачи
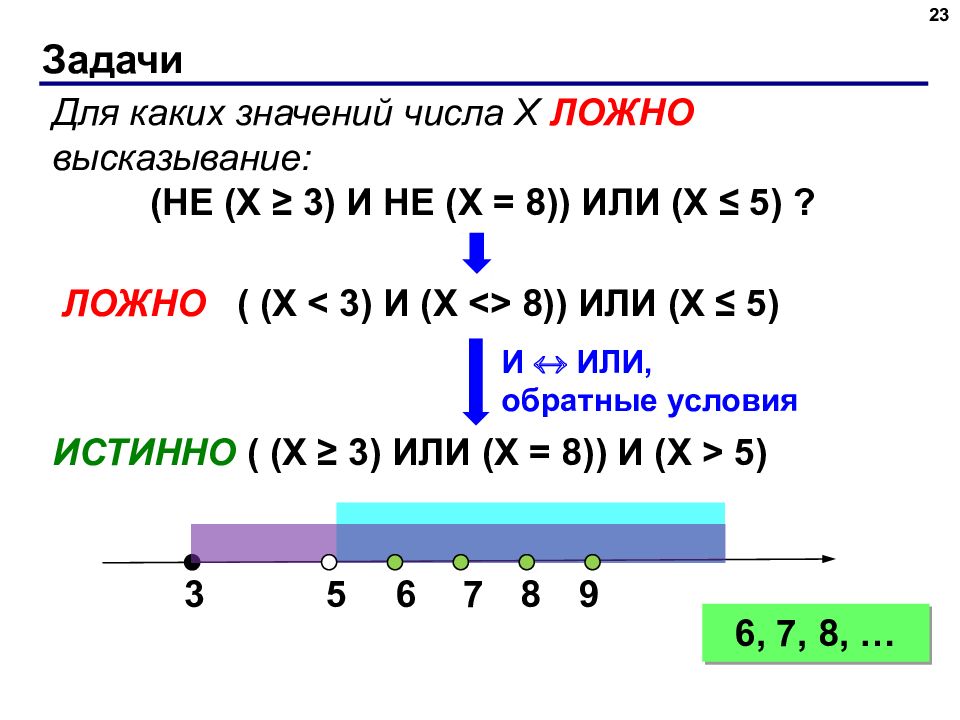
23 Для каких значений числа X ЛОЖНО высказывание: (НЕ (X ≥ 3) И НЕ (X = 8)) ИЛИ ( X ≤ 5 ) ? ЛОЖНО ( (X < 3) И (X <> 8)) ИЛИ ( X ≤ 5 ) 3 6, 7, 8, … ИСТИННО ( (X ≥ 3) ИЛИ (X = 8)) И ( X > 5 ) 8 7 5 6 9 И ИЛИ, обратные условия
Слайд 24: Что такое множество?
24 Множество – некоторый набор элементов, каждый из которых отличается от остальных. пустое множество: конечное число элементов: буквы русского алфавита бесконечное число элементов: натуральные числа Как задать множество? перечислением элементов { Вася, Петя, Коля } логическим выражением: { x : x > 0 }
Слайд 25: Изображение множеств
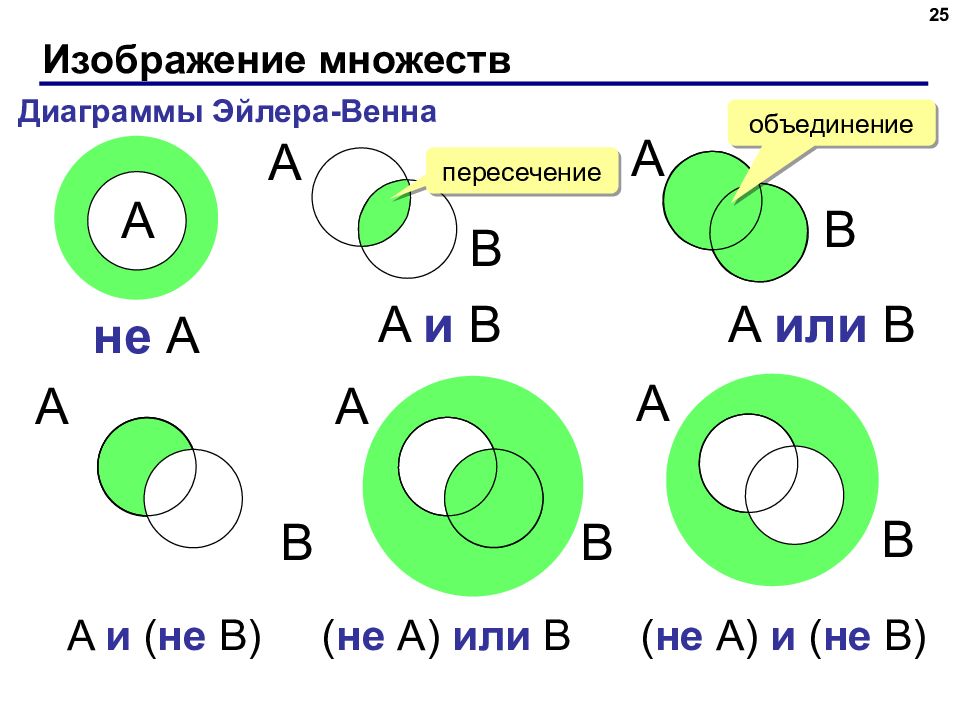
25 Диаграммы Эйлера-Венна A B A B A A и B A B A или B ( не A) или B A B пересечение объединение A и ( не B) A B не A ( не A) и ( не B)
Слайд 26: Количество элементов множеств
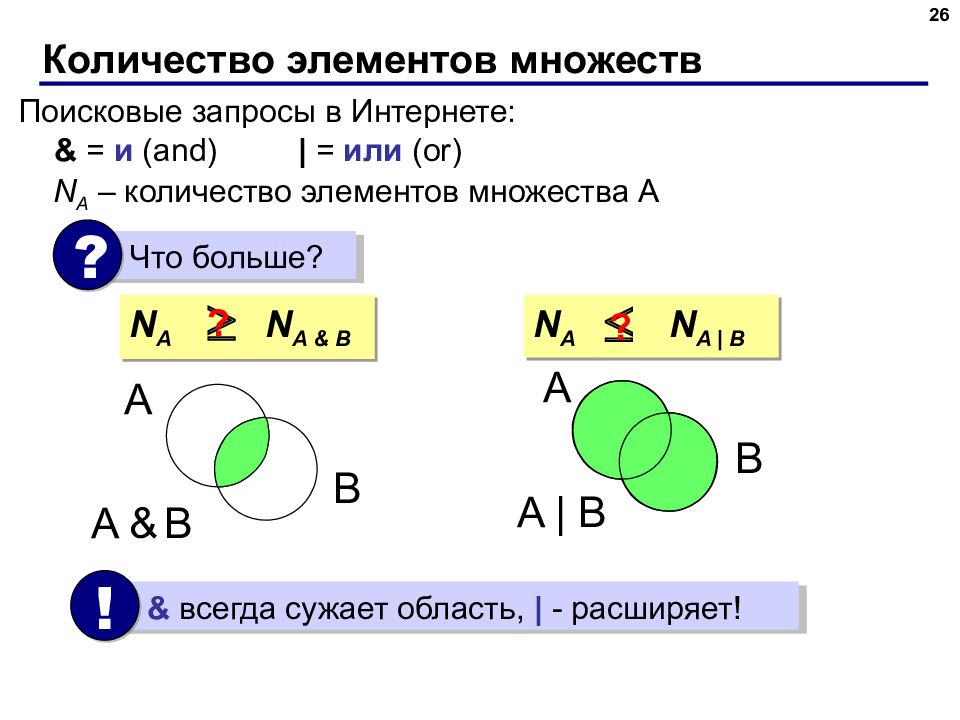
26 Поисковые запросы в Интернете: & = и ( and ) | = или ( or ) Что больше? ? N A – количество элементов множества A N A N A & B ? A B A & B N A N A | B ? A B A | B & всегда сужает область, | - расширяет! !
Слайд 27: Задачи
27 В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. А: принтеры & сканеры & продажа Б: принтеры | продажа В: принтеры & продажа Г: принтеры | сканеры | продажа АВБГ
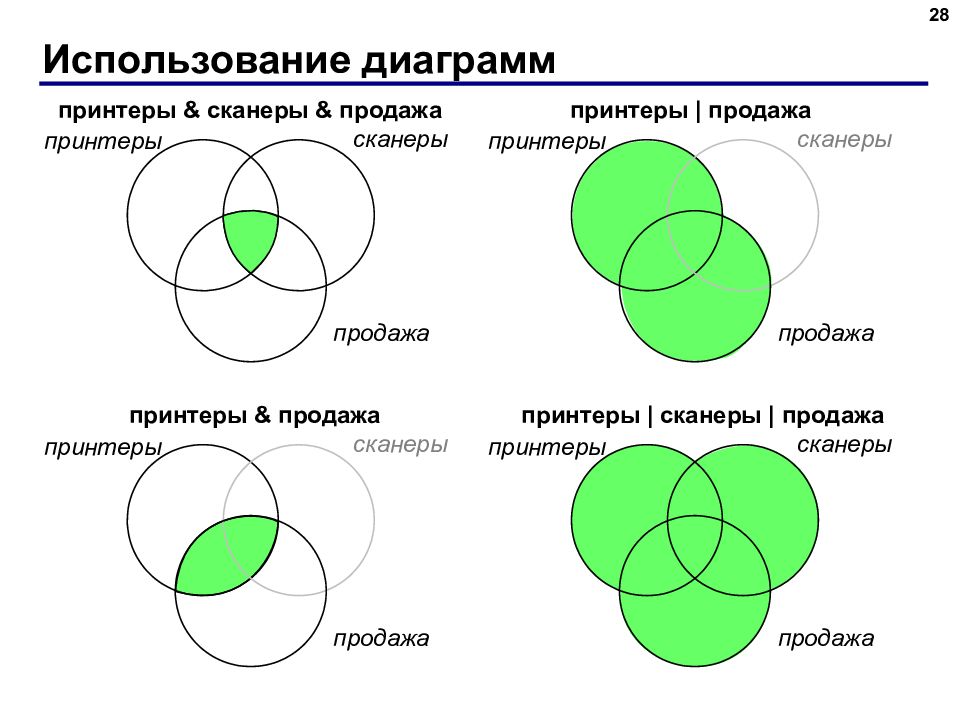
Слайд 28: Использование диаграмм
28 принтеры сканеры продажа принтеры & сканеры & продажа принтеры сканеры продажа принтеры | продажа принтеры сканеры продажа принтеры & продажа принтеры сканеры продажа принтеры | сканеры | продажа
Слайд 29: Задачи
29 В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. А: принтеры & сканеры & продажа Б: (принтеры & сканеры) | продажа В: (принтеры | сканеры) & продажа Г: принтеры | сканеры | продажа ГБВА
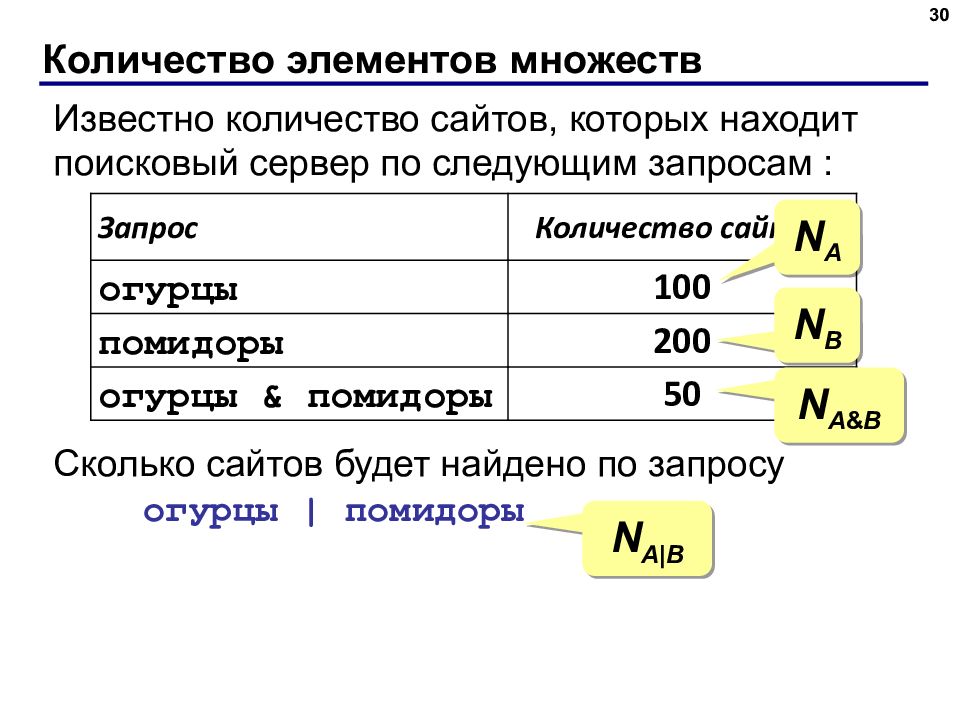
Слайд 30: Количество элементов множеств
30 Известно количество сайтов, которых находит поисковый сервер по следующим запросам : Сколько сайтов будет найдено по запросу огурцы | помидоры Запрос Количество сайтов огурцы 100 помидоры 200 огурцы & помидоры 50 N A N B N A & B N A|B
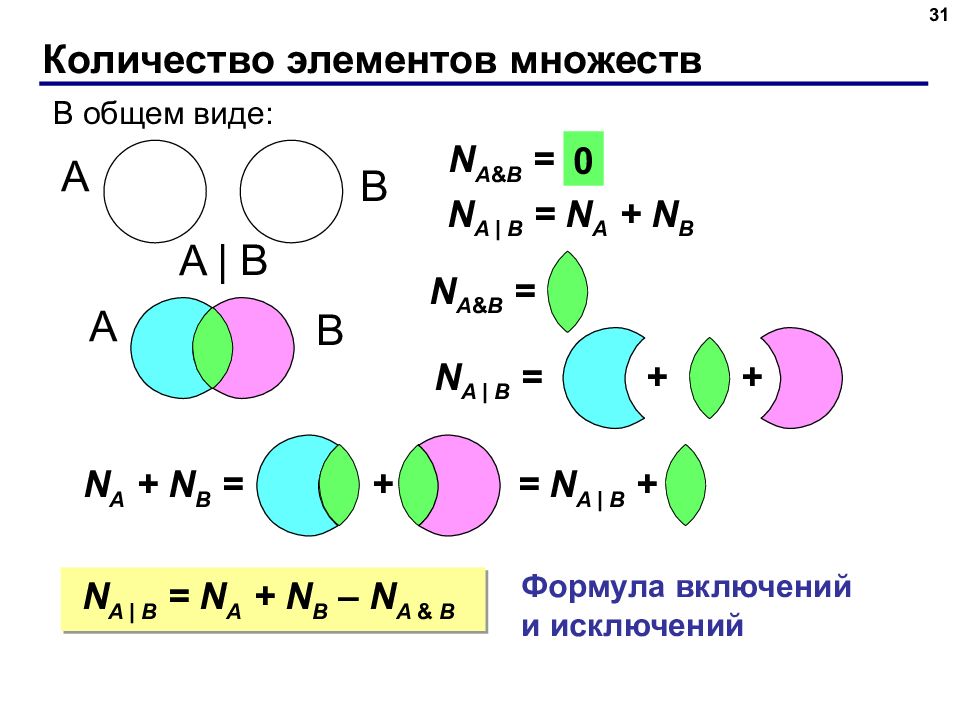
Слайд 31: Количество элементов множеств
31 A B В общем виде: N A & B = ? 0 N A | B = N A + N B A B N A | B = + + N A + N B = N A & B = N A | B = N A + N B – N A & B Формула включений и исключений + = N A | B + A | B
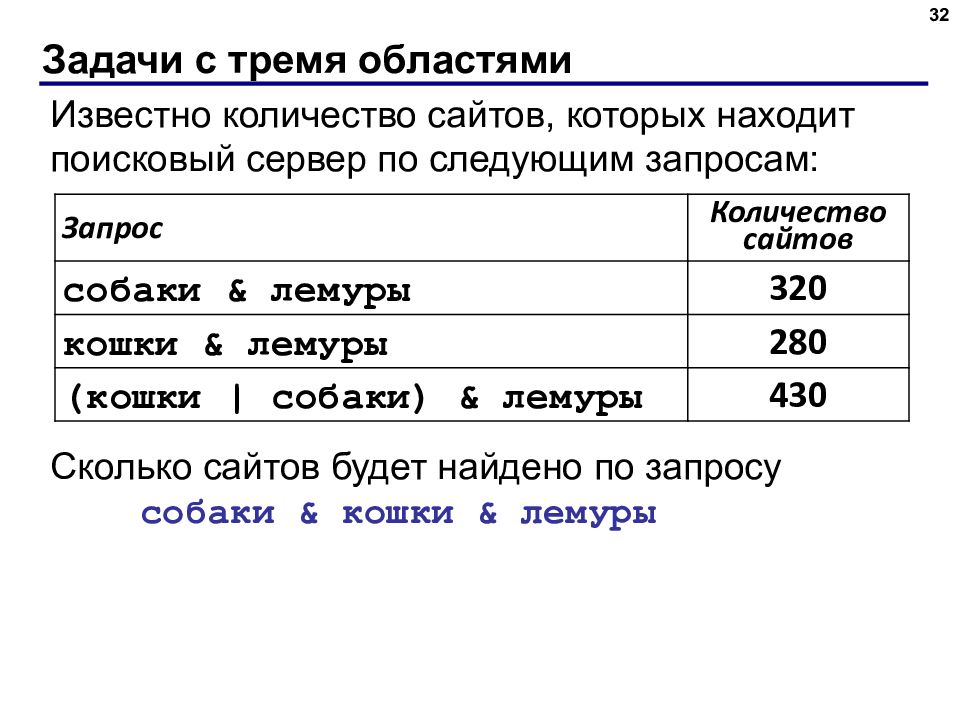
Слайд 32: Задачи с тремя областями
32 Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов будет найдено по запросу собаки & кошки & лемуры Запрос Количество сайтов собаки & лемуры 320 кошки & лемуры 280 ( кошки | собаки) & лемуры 430
Слайд 33: Задача с тремя областями
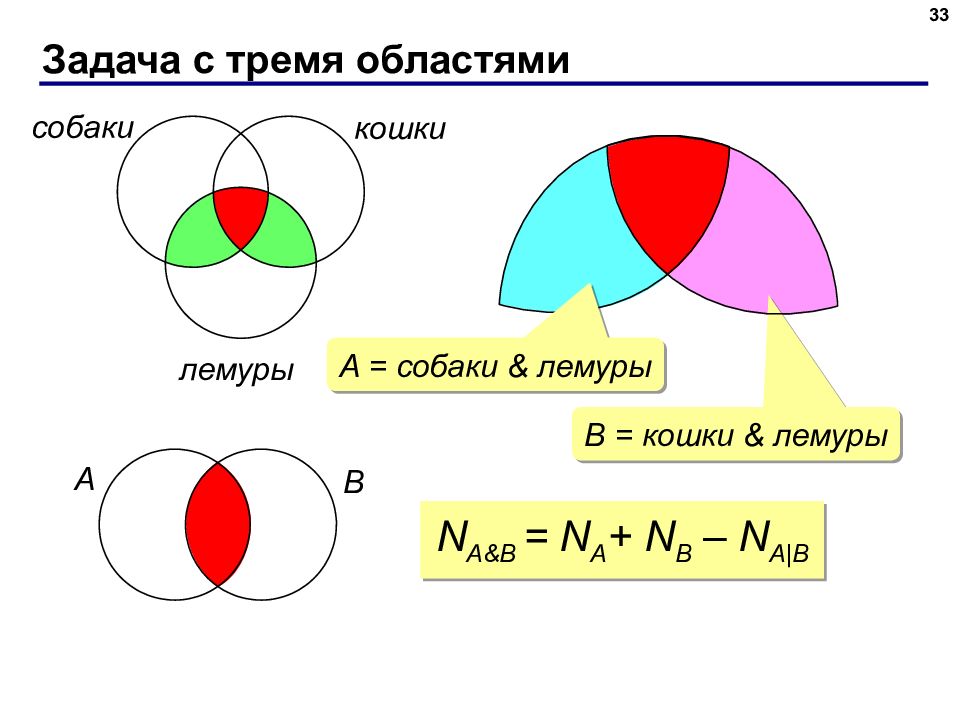
33 собаки кошки лемуры B = кошки & лемуры A B N A&B = N A + N B – N A|B A = собаки & лемуры
Слайд 34: Задачи с тремя областями
34 Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов будет найдено по запросу собаки & кошки & лемуры Запрос Количество сайтов собаки & лемуры 320 кошки & лемуры 280 ( кошки | собаки) & лемуры 430 A B A | B A & B Общее условие с & можно отбросить ! ! N A & B = N A + N B – N A|B = 320 + 280 – 430 = 170
Слайд 35: Задачи с тремя областями
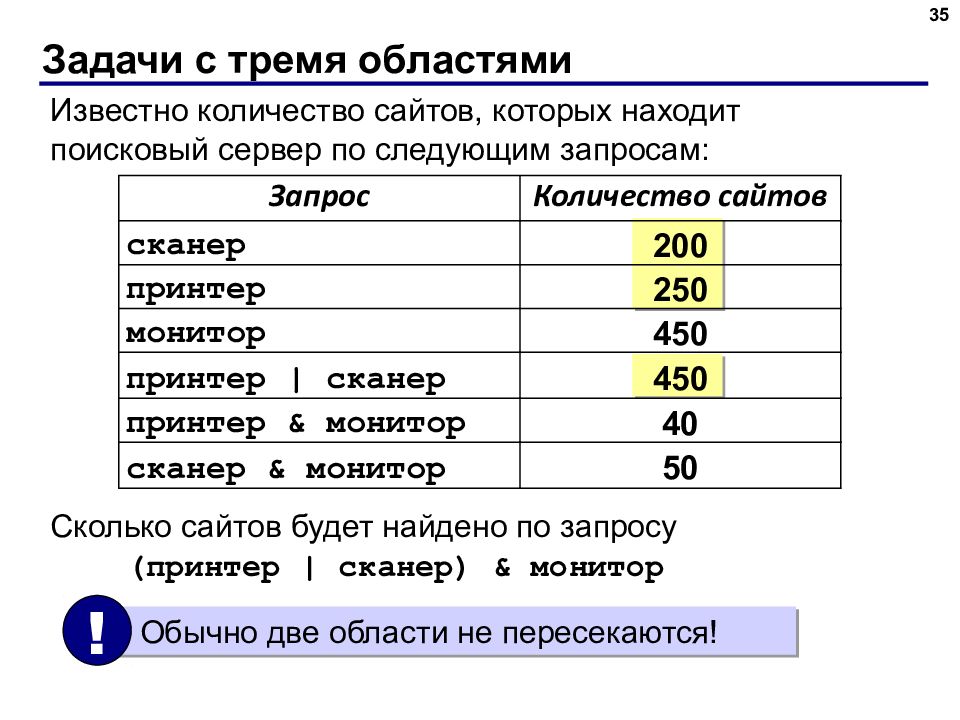
Известно количество сайтов, которых находит поисковый сервер по следующим запросам: Сколько сайтов будет найдено по запросу (принтер | сканер) & монитор Задачи с тремя областями 35 Запрос Количество сайтов сканер 200 принтер 250 монитор 450 принтер | сканер 450 принтер & монитор 40 сканер & монитор 50 Обычно две области не пересекаются! !
Слайд 36: Задачи с тремя областями
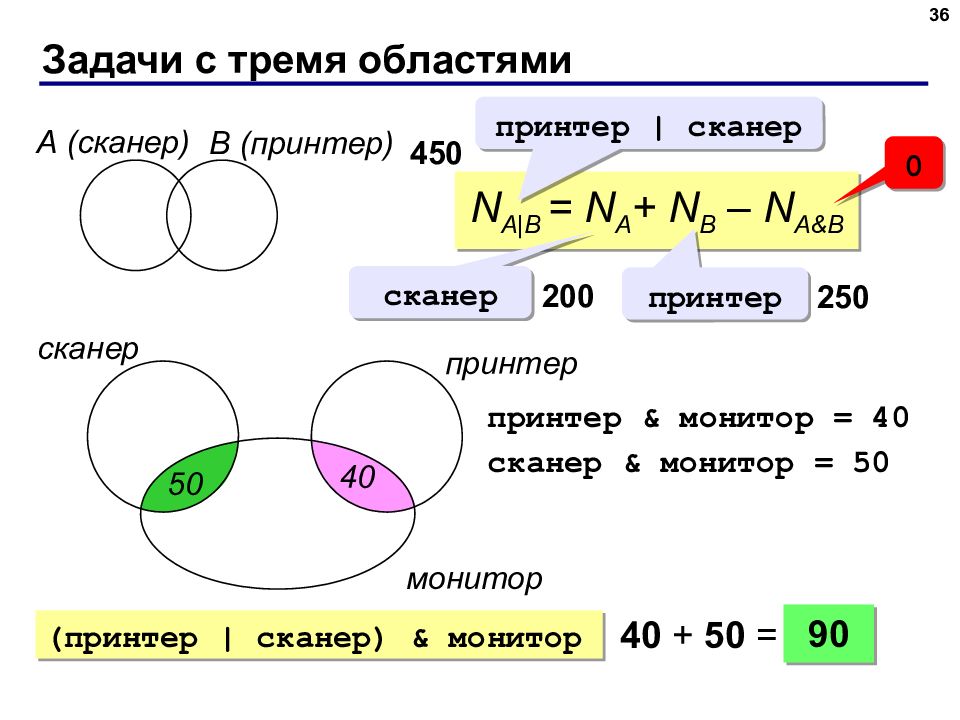
36 А (сканер) B (принтер) N A|B = N A + N B – N A&B принтер | сканер 450 сканер принтер 2 0 0 250 0 сканер принтер монитор 90 40 + 50 = принтер & монитор = 40 сканер & монитор = 50 50 40 (принтер | сканер) & монитор
Слайд 37: Задача 3а (Логическое высказывание)
37 Найдите значение выражения 1010011 2 + 322 8 - A1 16 Ответ запишите в десятичной системе счисления. Решение: Переведем все числа в десятичную систему счисления через развернутую форму записи числа: 1010011 2 = 1*2 6 + 1*2 4 + 1*2 1 + 1*2 0 = 64+16+2+1=83 322 8 = 3*8 2 + 2*8 1 + 2*8 0 = 192 + 16 + 2 = 210 A1 16 = 10*16 1 + 1*16 0 = 160 + 1 = 161 Вычислим значение выражения 83 + 210 – 161 = 132 Ответ: 132
Слайд 38: Задача 3а (Логическое высказывание)
38 Напишите наименьшее число x, для которого истинно высказывание: (x > 23) И НЕ (x делится на 8) Решение: Операция НЕ перед выражением меняет его смысл на противоположный, то есть высказывание будет звучать: (x > 23) И (x не делится на 8) Операция И означает, что условия действуют одновременно, то есть мы должны найти наименьшее число, которое не делится на 8 и большее 23 Число 24 > 23, но делится на 8! Возьмем число больше. Число 25 не делится на 8! Ответ: 25
Слайд 39: Задача 3б (Логическое высказывание)
39 Напишите наименьшее число x, для которого истинно высказывание: (x > 31) И НЕ (сумма цифр числа x больше 8) Решение: Операция НЕ перед выражением меняет его смысл на противоположный, то есть высказывание будет звучать: (x > 31) И (сумма цифр числа x <= 8) Операция И - условия действуют одновременно. Минимальное число 32. Его сумма цифр 3 +2=5 < 8. Условие выполнено! Ответ: 32
Слайд 40: Задача 3в (Логическое высказывание)
40 Напишите наибольшее число x, для которого истинно высказывание: НЕ (x > 19) И НЕ (x чётное) Решение: Операция НЕ перед выражением меняет его смысл на противоположный, то есть высказывание будет звучать: (x <= 31) И ( x нечётное) Операция И - условия действуют одновременно. Максимальное число 31 и оно нечётное! Ответ: 31
Слайд 41: Задача 3г (Логическое высказывание)
41 Напишите наибольшее число x, для которого ложно высказывание: (x > 95) ИЛИ НЕ (x кратно 14) Решение: Операция НЕ перед выражением меняет его смысл на противоположный, то есть высказывание будет звучать: (x <= 31) ИЛИ ( x не кратно 16) Операция ИЛИ – достаточно одного условия для истинности выражения, но т.к. у нас выражение должно быть ложно, то должны быть ложны оба условия. Нам надо найти наибольшее число X<=95 и кратное 16. 16 кратны числа 16, 32, 48, 64, 80, 96 … Наибольшее число, не превышающее 95 – это 80. Ответ: 80
Слайд 42: Задача 3д (Логическое высказывание)
42 Напишите наименьшее двузначное число x, для которого истинно высказывание: (ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И НЕ (ЧИСЛО ДЕЛИТСЯ НА 6) И (ЧИСЛО ДЕЛИТСЯ НА 7) Решение: Применяем операцию НЕ и получаем выражение: (ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И (ЧИСЛО НЕ ДЕЛИТСЯ НА 6) И (ЧИСЛО ДЕЛИТСЯ НА 7) Ищем наименьшее двузначное число, у которого первая цифра нечетная ( 1,3,5,7,9), которое делится на 7 и не делится на 6. 14 – двузначное, первая цифра нечетная, делится на 7 и не делится на 6. Ответ: 14
Слайд 43: Задача 3е (Логическое высказывание)
43 Найдите наибольшее натуральное двухзначное число X, для которого истинно высказывание: ((X < 25) ИЛИ НЕ (X > 58)) И (X чётное) Решение: Применяем операцию НЕ и получаем выражение: ((X < 25) ИЛИ (X <= 58)) И (X чётное) Ищем наибольшее четное двузначное число <=58. Наибольшее число 58 чётное! Ответ: 58
Слайд 44: Задача 3 (Справочная информация)
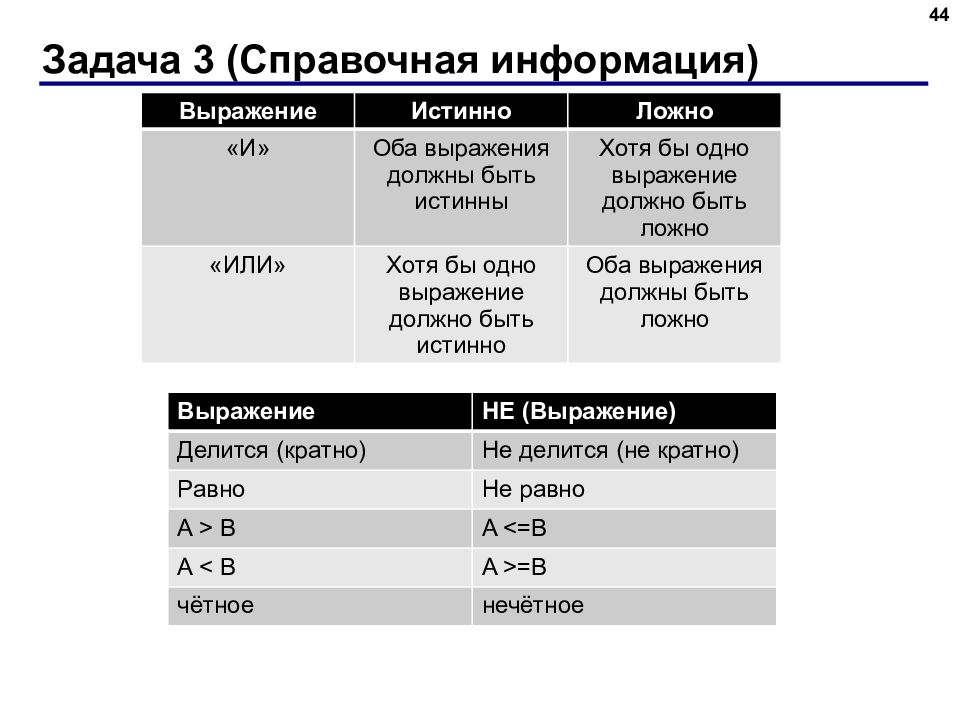
44 Выражение Истинно Ложно «И» Оба выражения должны быть истинны Хотя бы одно выражение должно быть ложно «ИЛИ» Хотя бы одно выражение должно быть истинно Оба выражения должны быть ложно Выражение НЕ (Выражение) Делится (кратно) Не делится (не кратно) Равно Не равно A > B A <=B A < B A >=B чётное нечётное
Слайд 45: Задача 3 (самостоятельно)
45 1) Найдите количество двухзначных натуральных чисел X, для которых ложно высказывание: (X >= 47) И НЕ ((X кратно 4) И НЕ (Х кратно 8)) 2) Найдите количество трехзначных натуральных чисел X, для которых истинно высказывание: (X >= 250) И (X кратно 30) И НЕ (Х < 700) 3) Найдите количество двухзначных натуральных чисел X, для которых ложно высказывание: НЕ (X >= 74) И НЕ (X чётное) 4) Найдите количество двухзначных натуральных чисел X, для которых ложно высказывание: (X <= 81) И НЕ (X оканчивается на четную цифру)
Слайд 46: Задача 3 (самостоятельно)
46 5) Напишите наибольшее двузначное число x, для которого истинно высказывание: (ТОЛЬКО ПЕРВАЯ ЦИФРА ЧЁТНАЯ) И НЕ (ЧИСЛО ДЕЛИТСЯ НА 3) И (ЧИСЛО ДЕЛИТСЯ НА 5) 6) Напишите наименьшее двузначное число x, для которого истинно высказывание: (ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И НЕ (ЧИСЛО ДЕЛИТСЯ НА 4) И (ЧИСЛО ДЕЛИТСЯ НА 5) 7) Напишите наибольшее двузначное число x, для которого истинно высказывание: (ТОЛЬКО ПЕРВАЯ ЦИФРА НЕЧЁТНАЯ) И НЕ (ЧИСЛО ДЕЛИТСЯ НА 5) И (ЧИСЛО ДЕЛИТСЯ НА 4)
Последний слайд презентации: ОГЭ Информатика: Задача 3 (самостоятельно)
47 8) Напишите наибольшее число x, для которого истинно высказывание: НЕ (x ≥ 38) И НЕ(x не делится на 17) 9) Напишите наименьшее число x, для которого истинно высказывание: НЕ (x ≤ 39) И (x кратно 12) 10) Напишите наименьшее число x, для которого ложно высказывание: НЕ (x > 73) ИЛИ НЕ(x кратно 18) 11) Напишите наибольшее число x, для которого ложно высказывание: (x > 72) ИЛИ (x не делится на 11)