Операции над Массивами Переписываем всё, с примерами и табличками
При работе с большими объёмами данных в программировании приходится использовать массивы, списки, вектора… в зависимости от поставленной задачи. Чтобы лучше взаимодействовать с данными больших хранилищ информации(массивы), следует овладеть приёмами, позволяющими манипулировать данными внутри массивов: Нахождение наибольшего и наименьшего элемента, сдвиги массивов, сортировки массивов.
1. Нахождение наибольшего и наименьшего элемента: Для начала создаём переменную для того, чтобы запоминать в неё нужный элемент массива. Если мы ищем минимальное значение, то переменная должна быть заранее больше всех элементов массива. Если ищем максимальное, то переменная должна быть меньше всех элементов массива.
В цикле мы проверяем, является ли переменная minimum больше первого элемента массива, и если ДА – её надо уменьшить. Также нужно запомнить порядковый номер этого элемента в отдельную переменную, например index. После проверки первого элемента в цикле проверяются и все остальные. После работы цикла в переменной index будет храниться порядковый номер самого маленького элемента массива, а в переменной minimum – самое маленькое число. Максимум ищется аналогично, нужно запустить такой же цикл, в условии поменять знак > на знак <, и переменная maximum изначально должна быть очень маленькой.
2. Сдвиги массивов. Сдвиг массива, это когда все элементы меняют свой порядковый номер на следующий, а первый последний элемент перемещается в начало массива, это сдвиг вправо. И соответственно, если все элементы меняют порядковый номер на предыдущий, а первый элемент(нулевой) перемещается в конец списка – это сдвиг влево.
При запуске такого алгоритма, важно понимать, что цикл работает не со всем массивом. Чтобы сдвинуть элемент вправо используется строка x[ i ] = x[i+1]. Мы берём следующий элемент и сохраняем на место предыдущего. Но если цикл выполняется 10й раз, а в массиве всего 10 элементов, то x[i+1] – это 11й элемент, которого не существует, - произойдёт ошибка. Чтобы избежать такой ошибки – цикл выполняется на 1 меньше, чем размер массива. Либо, начинается не с 0 а с 1, если мы используем x[i-1].
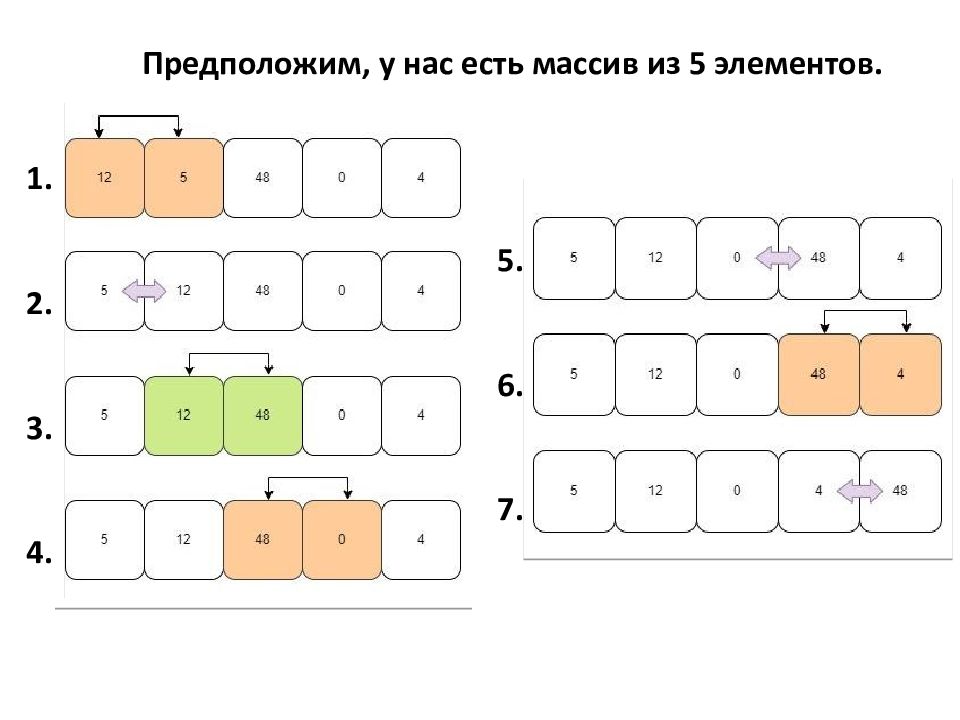
3. Сортировка массивов. Сортировка массива, это когда все его элементы выстраиваются в определённом порядке. Существует много способов сортировать массивы, рассмотрим 2 самых простых способа: Сортировка выбором и Пузырьковая сортировка. 1. Пузырьковая сортировка В пузырьковой сортировке мы сравниваем 2 соседних элемента. Если они стоят не в том порядке – меняем их местами. После проверяется вторая пара элементов, третья… пока цикл не дойдёт до конца массива. После первого такого прохода процесс начинается сначала и так до тех пор, пока все элементы не будут стоять в нужном нам порядке.
1. 2. 3. 4. 5. 6. 7. Предположим, у нас есть массив из 5 элементов.
Чтобы понять, когда пора прекращать сортировку – обычно создают дополнительную переменную,которая увеличивается каждый раз, когда происходила замена, и обнуляется перед каждым новым запуском. Если в конце переменная насчитала 0 замен – значит всё уже стоит на нужных местах и пора прерывать сортировку: В этом случае цикл также работает не до последнего элемента, а до предпоследнего(из-за x[i+1] ).
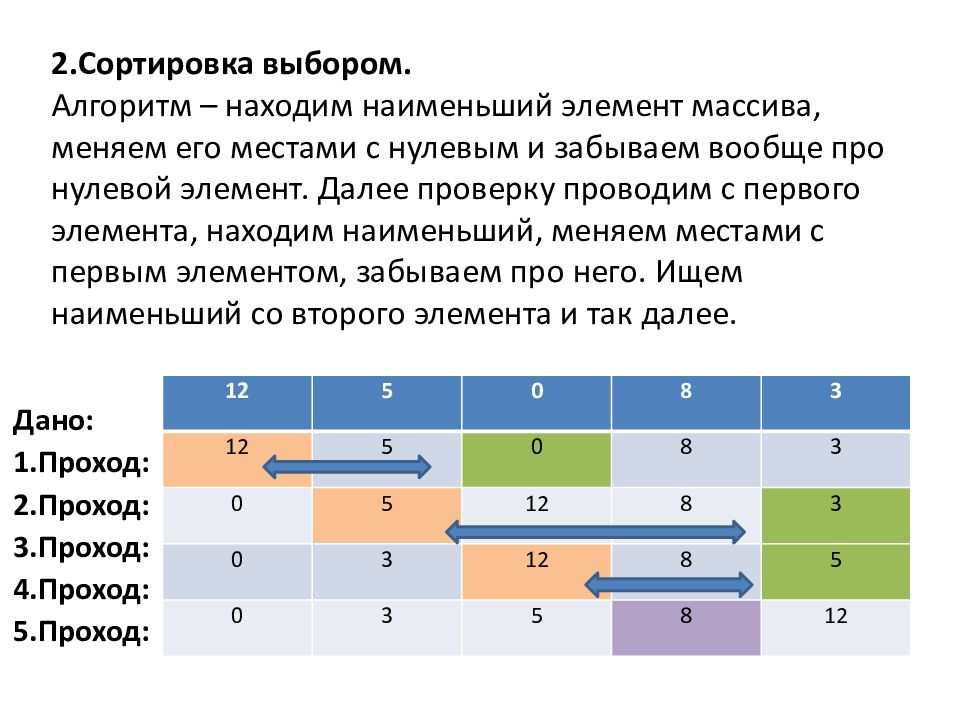
2.Сортировка выбором. Алгоритм – находим наименьший элемент массива, меняем его местами с нулевым и забываем вообще про нулевой элемент. Далее проверку проводим с первого элемента, находим наименьший, меняем местами с первым элементом, забываем про него. Ищем наименьший со второго элемента и так далее. 12 5 0 8 3 12 5 0 8 3 0 5 12 8 3 0 3 12 8 5 0 3 5 8 12 Дано: 1.Проход: 2.Проход: 3.Проход: 4.Проход: 5.Проход:
При такой сортировке очень помогает алгоритм нахождения наибольшего и наименьшего элемента массива, с запоминанием его порядкового номера. Вот так выглядит весь алгоритм, если учитывать, что findMin (); это функция, которая находит наименьшее значение, как на 3м слайде. Обратите внимание, на 3м слайде цикл начинается с « n » а не с 0. Это сделано для того, чтобы не искать минимальное значение среди отсортированных значений.
