Операции над множествами: пересечение, объединение, дополнение 8ТВиС
Объединение Два или несколько множеств можно объединить в одно. Получится новое множество, которое называют объединением. Для обозначения объединения используют значок U.
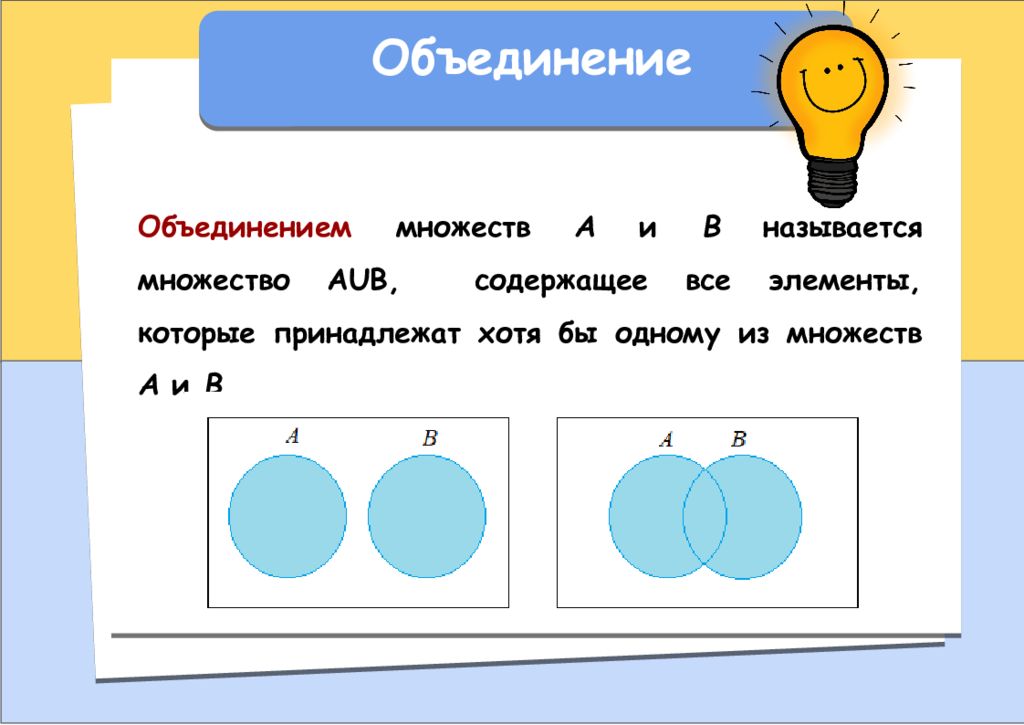
Объединение Объединением множеств А и В называется множество АUВ, содержащее все элементы, которые принадлежат хотя бы одному из множеств А и В.
Пример №1 Пусть даны множества: А={1, 2, 3, 4} и В={2, 3, 5, 7}. Найдите объединение множеств А и В.
Пусть даны множества: А={1, 2, 3, 4} и В={2, 3, 5, 7}. Найдите объединение множеств А и В. Ответ: При объединении множеств общие элементы учитываются один раз. Пример №1
Объединение Отрезок и полуинтервал – числовые множества. Их объединение состоит из всех точек числовой прямой, принадлежащих хотя бы одному из этих множеств.
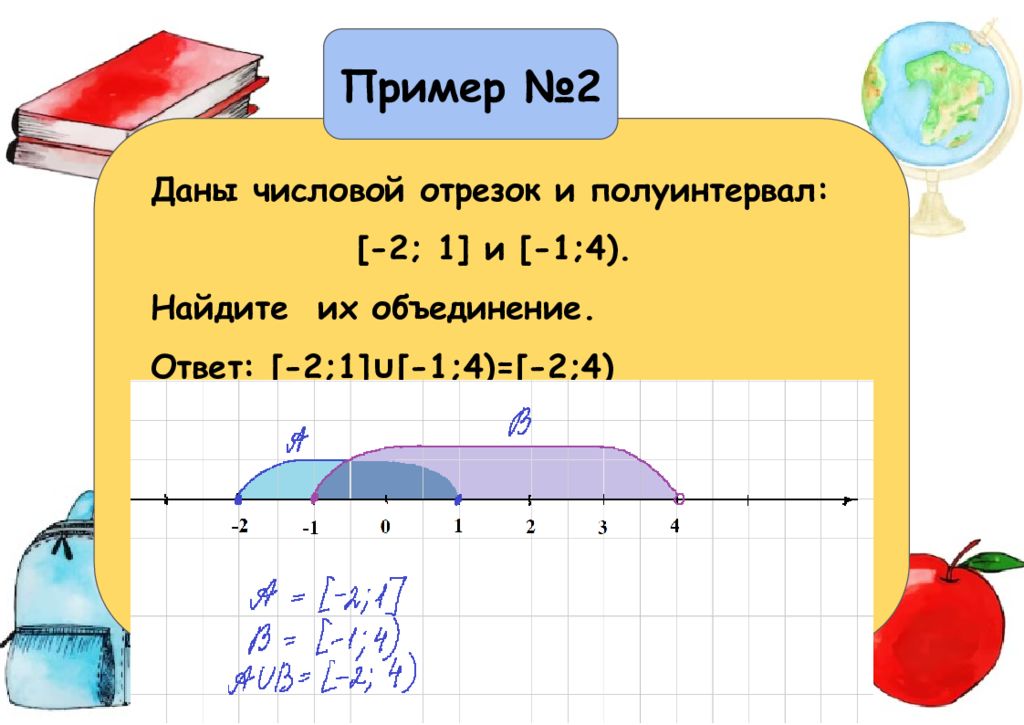
Пример №2 Даны числовой отрезок и полуинтервал: [-2; 1] и [-1;4). Найдите их объединение.
Пример №2 Даны числовой отрезок и полуинтервал: [-2; 1] и [-1;4). Найдите их объединение. Ответ: [-2;1]∪[-1;4)=[-2;4)
Пересечение Разные множества могут иметь общие элементы. Эти элементы тоже образуют новое множество, которое называют пересечением данных множеств. Для обозначения пересечения множеств используют значок ∩.
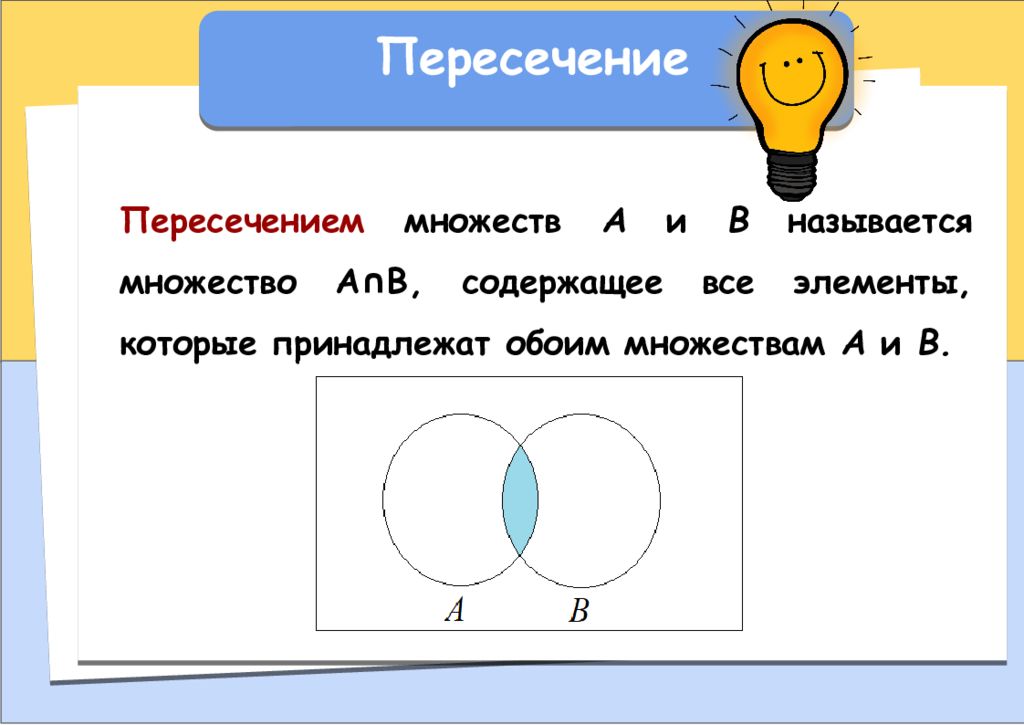
Пересечение Пересечением множеств А и В называется множество А∩В, содержащее все элементы, которые принадлежат обоим множествам А и В.
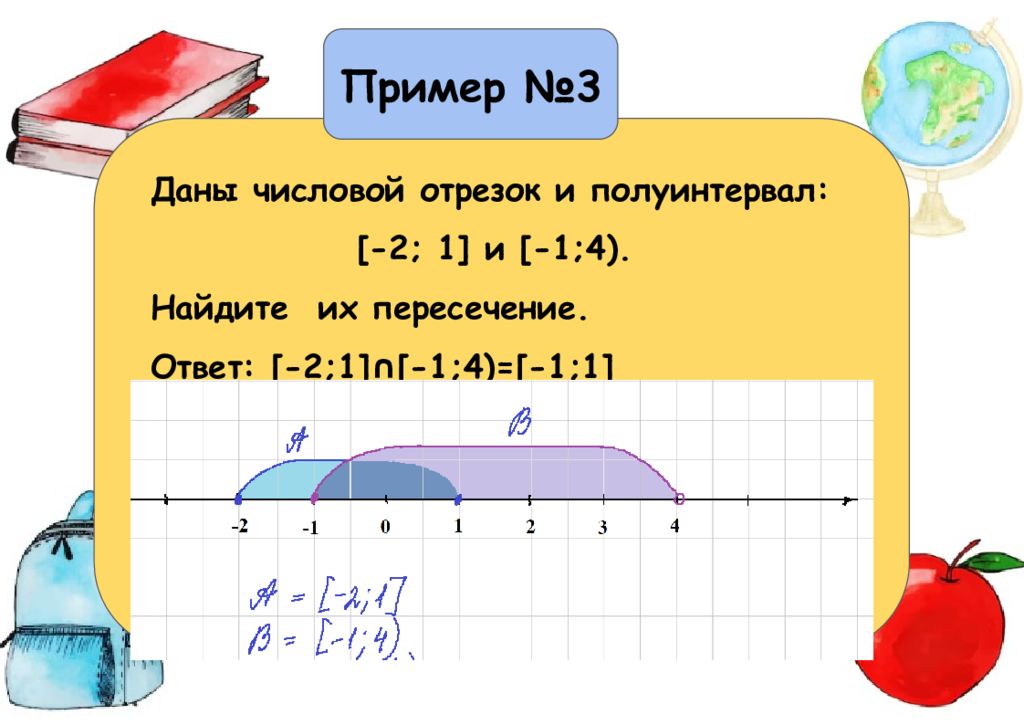
Пример №3 Даны числовой отрезок и полуинтервал: [-2; 1] и [-1;4). Найдите их пересечение.
Пример №3 Даны числовой отрезок и полуинтервал: [-2; 1] и [-1;4). Найдите их пересечение. Ответ: [-2;1]∩[-1;4)=[-1;1]
Если множества не имеют одинаковых элементов, то их пересечение является пустым множеством.
Пример №4 Даны множества: А={1; 3; 5; 7; …} и B={2; 4; 6; 8; …}. Найдите пересечение множеств А и В.
Пример №4 Ответ: А={1; 3; 5; 7; …}-множество нечётных чисел; B={2; 4; 6; 8; …} - множество чётных чисел. А∩В=∅
Дополнение
Пример №5
В={1, 2, 3, 4, 5, 6} А={3, 4, 5, 6}. Ответ: Пример №5
