Слайд 2: Определенный интеграл
a f ( x ) dx F ( x ) b F ( b ) F ( a ) b a - формула Ньютона – Лейбница a - нижний предел интегрирования, b - верхний предел интегрирования.
Слайд 3: Для вычисления определённого интеграла f ( x ) dx,
нужно: 1. Найти какую- нибудь первообразную для функции (найти неопределенный интеграл от функции , в котором можно принять C=0 ); 2. В полученном выражении подставить вместо x сначала верхний предел, а затем нижний предел, и из результата первой подстановки вычесть результат второй. b a Для вычисления определённого интеграла f ( x ) dx, b F ( x ) f ( x ) a
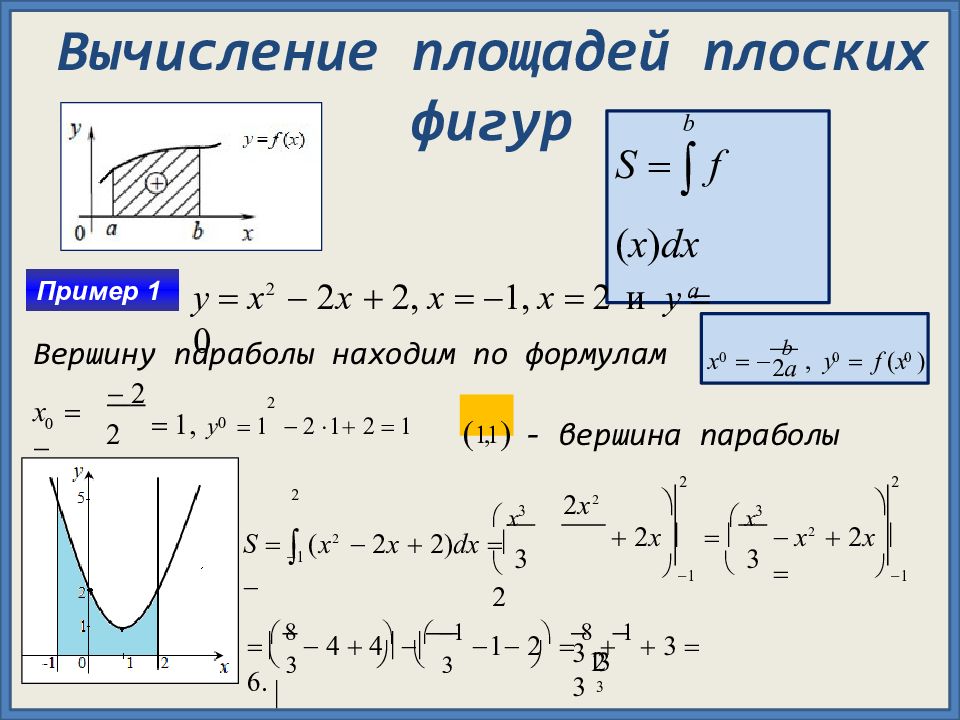
Слайд 4: Вычисление площадей плоских
фигур b S f ( x ) dx a Пример 1 y x 2 2 х 2, x 1, x 2 и y 0 Вершину параболы находим по формулам 0 0 0 2 а х b, y f ( x ) 0 2 2 1 х 2 0 1, у 1 2 1 2 1 1,1 - вершина параболы 2 1 2 1 2 1 3 3 2 x 2 2 x 2 x 2 x 2 x 3 x 3 S ( x 2 2 x 2) dx 3 3 3 3 8 4 4 1 1 2 8 1 3 6. 3
Слайд 5
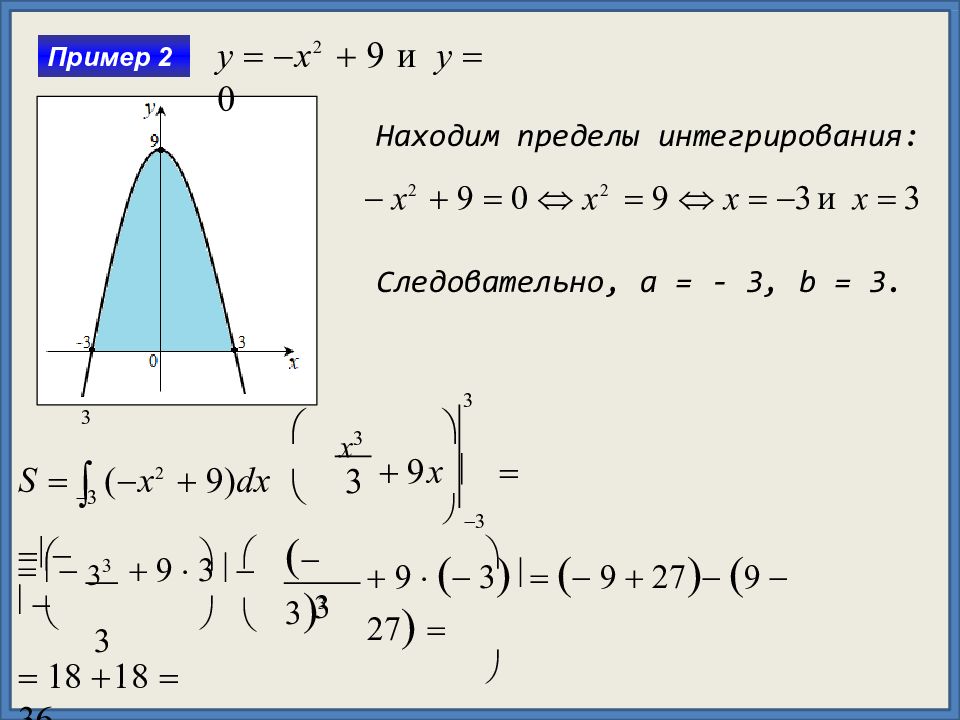
y x 2 9 и y 0 Пример 2 3 3 3 3 3 9 x x 3 S ( x 2 9) dx 9 3 9 27 9 27 3 9 3 3 3 3 3 3 18 18 36 Находим пределы интегрирования: x 2 9 0 x 2 9 x 3 и x 3 Следовательно, a = - 3, b = 3.
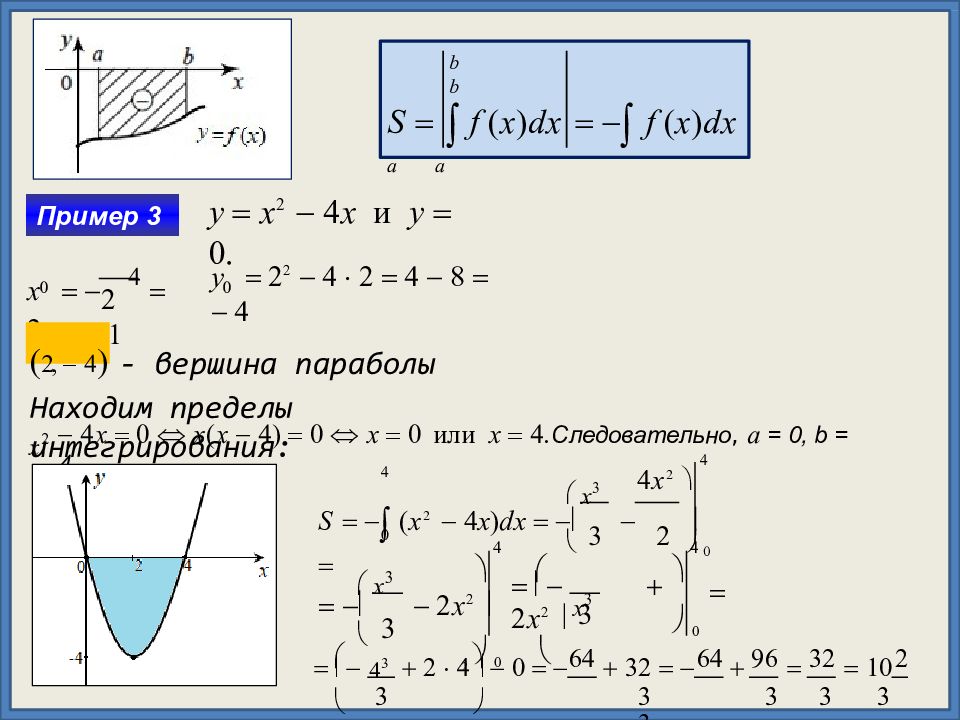
Слайд 6: S f ( x ) dx f ( x ) dx a a
b b S f ( x ) dx f ( x ) dx a a Пример 3 y x 2 4 х и y 0. 0 0 2 1 y 2 2 4 2 4 8 4 х 4 2, 2, 4 - вершина параболы Находим пределы интегрирования: x 2 4 х 0 x ( x 4) 0 x 0 или x 4. Следовательно, a = 0, b = 4. 4 0 4 4 x 2 x 3 S ( x 2 4 x ) dx 4 0 4 3 3 2 x 2 0 3 2 0 x 3 2 x 2 x 3 64 64 96 32 2 4 3 2 2 4 0 32 10 3 3 3 3 3 3
Слайд 7: Задание. Вычислить определенный интеграл
1 6 9 2. x dx x 5 7 x 6 dx 1
Слайд 8: Задание. Вычислить площадь криволинейной трапеции ограниченной линиями
y x 1, y 1, x 0, x 2 y x 2, y 0, x 1, x 2
Последний слайд презентации: Определенный интеграл: Самостоятельная работа
Вариант 1 Найдите первообразную f ( x ) 9 x 2 cos x Найдите неопределенный интеграл 157 dx Найдите неопределенный интеграл 9 x 5 dx Найдите интеграл 2 4 x 3 dx 1 Найдите интеграл 2 sin xdx 0