Политехнический институт Великий Новгород, 2025 г.
Образовательный интенсив Обучение решению планиметрических задач повышенной сложности (часть 2) Кондрушенко Е. М., зав. кафедрой алгебры и геометрии, кандидат пед. наук, доцент Бутц А. В., ассистент кафедры алгебры и геометрии
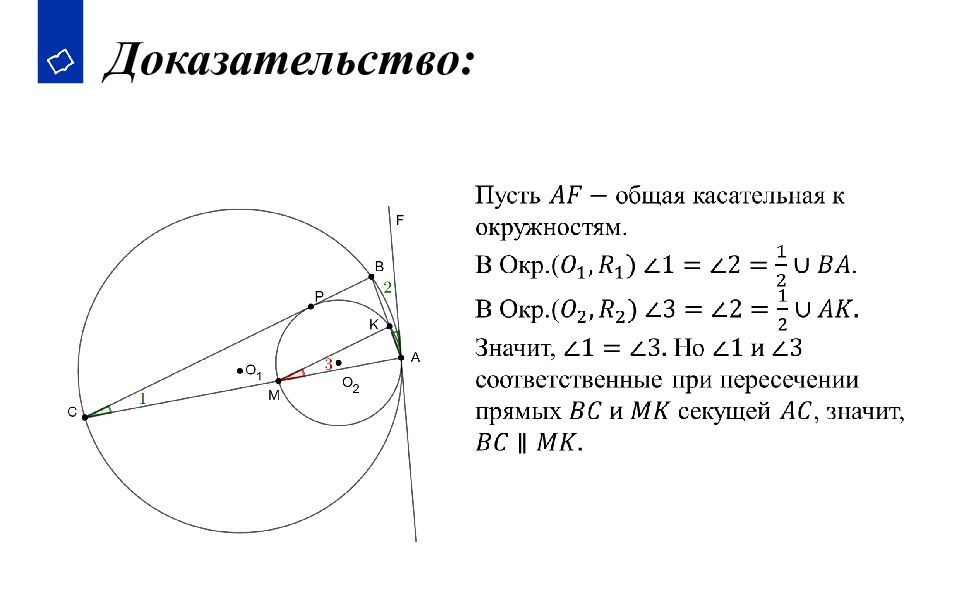
Ключевые задачи 1. Доказать, что хорды окружности, равны тогда и только тогда, когда они равноудалены от центра окружности. 2. Доказать, что любая прямая, проходящая через центр окружности, является ее осью симметрии. 3. Доказать, что если две параллельные прямые пересекают окружность каждая в двух точках, то дуги окружности, заключенные между этими прямыми, равны. 4. Доказать, что хорда окружности равна произведению диаметра на синус вписанного угла, опирающегося на эту хорду. 5. Доказать, что угол, образованный касательной и хордой, проходящей через точку касания, измеряется половиной дуги, заключенной между его сторонами.
6. Доказать, что угол, образованный двумя секущими с общей точкой, лежащей вне окружности (вершина угла), равен модулю полуразности угловых величин дуг окружности, заключенных внутри этого угла. 7. Доказать, что угол между пересекающимися хордами окружности равен полусумме угловых величин дуг, заключенных между сторонами данного угла и угла с ним вертикального. 8. Доказать, что если из некоторой точки вне окружности проведены к окружности касательная и секущая, то квадрат отрезка касательной с концами в общей точке и точке касания с окружностью равен произведению отрезков секущей с концами в общей точке и в точках пересечения секущей с окружностью.
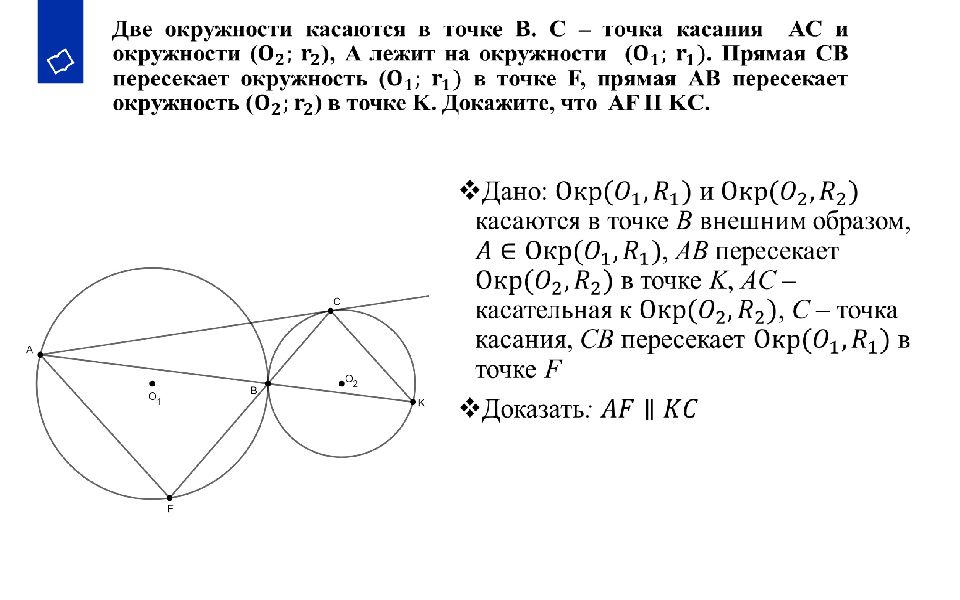
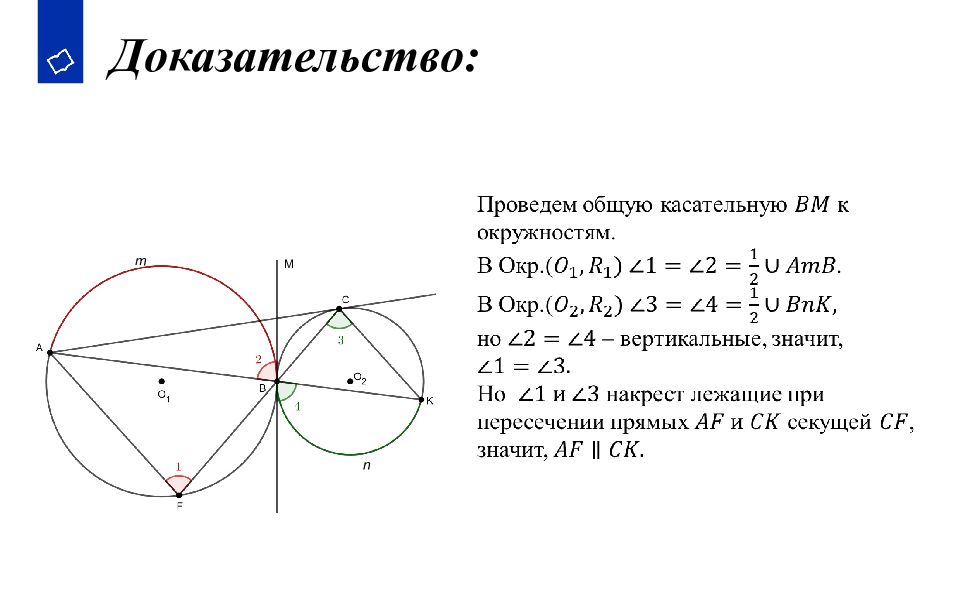
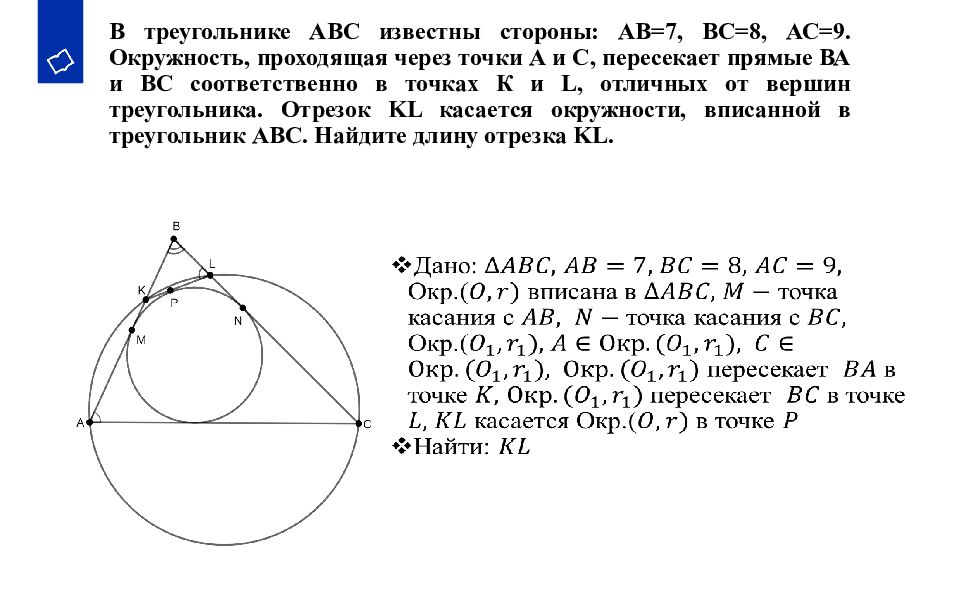
9. Доказать, что произведение секущих, проведённых из данной вне окружности точки, от этой точки до точек пересечения с окружностью, есть величина постоянная. 10. В треугольнике АВС ВС=а, АС=в, АВ=с, р - полупериметр треугольника. В треугольник вписана окружность, М – точка касания с АВ, N – с ВС, Р – с АС. Доказать, что АМ=р - а, В N =р - в, СР=р - с. 11. В треугольниках АВС и АДС точки В и Д лежат по одну сторону от АС, угол АВС равен углу АДС. Доказать, что точки А, В, Д, С лежат на одной окружности. 12. Доказать, что центры двух касающихся окружностей и точка касания лежат на одной прямой. 13. Две окружности с радиусами R и r касаются внешним образом. Найти длину отрезка общей касательной с концами в точках касания.
F
M m n
Решение.
Спасибо за внимание!
