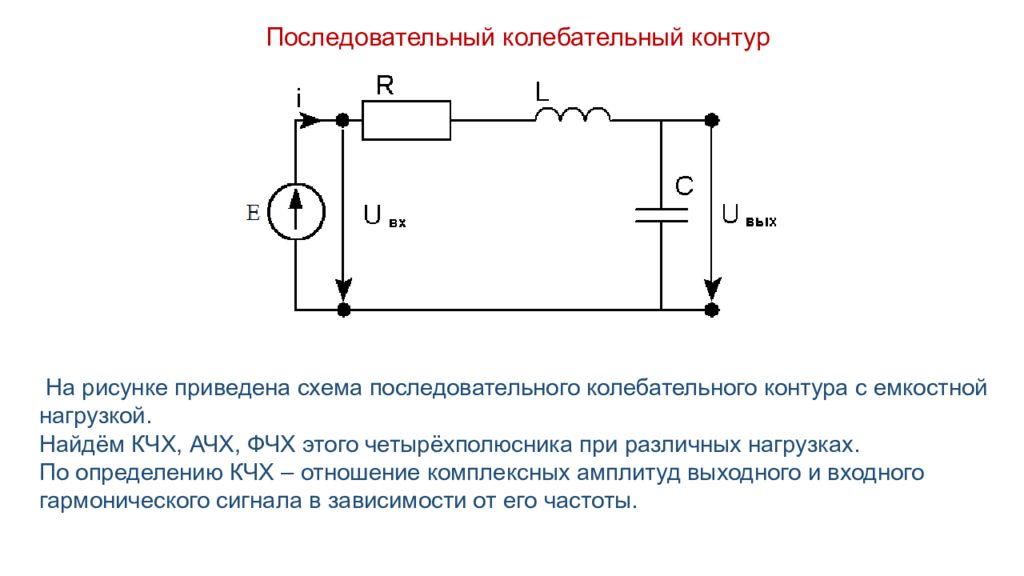
Последовательный колебательный контур На рисунке приведена схема последовательного колебательного контура с емкостной нагрузкой. Найдём КЧХ, АЧХ, ФЧХ этого четырёхполюсника при различных нагрузках. По определению КЧХ – отношение комплексных амплитуд выходного и входного гармонического сигнала в зависимости от его частоты.
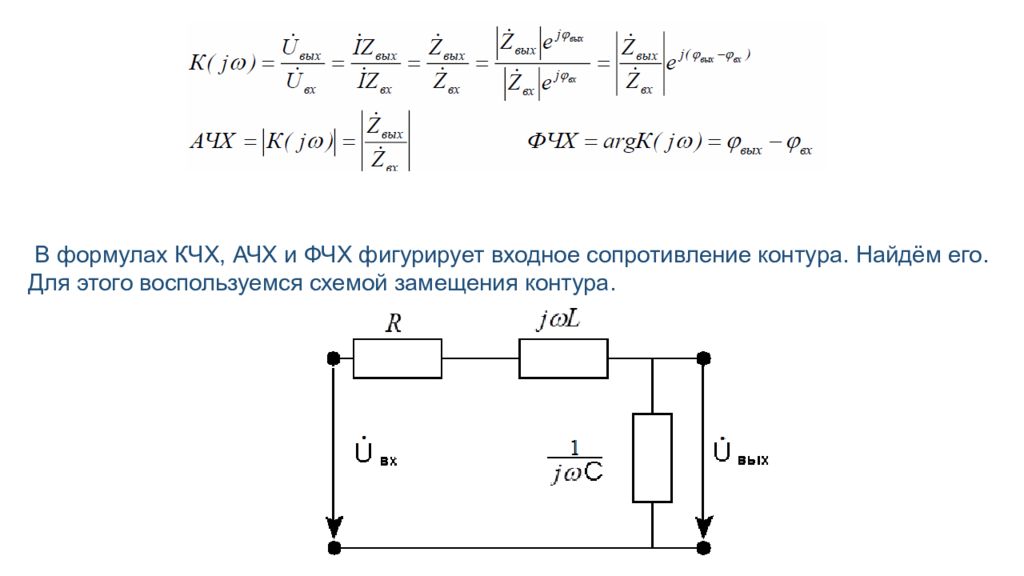
В формулах КЧХ, АЧХ и ФЧХ фигурирует входное сопротивление контура. Найдём его. Для этого воспользуемся схемой замещения контура.
- резонансная частота – частота, на которой входное сопротивление т.е. на этой частоте индуктивное и емкостное сопротивления равны по модулю и противоположны по знаку, и, следовательно, компенсируют друг друга. Кроме того, напряжения, выделяемые на индуктивности и емкости, так же равны друг другу по модулю и противоположны по знаку. Говорят, что в этом случае в контуре происходит резонанс напряжений, то есть суммарное падение напряжения на индуктивности и емкости равно нулю.
- - резонансная частота – частота, на которой входное сопротивление, т.е. на этой частоте индуктивное и емкостное сопротивления равны по модулю и противоположны по знаку, и, следовательно, компенсируют друг друга. Кроме того, напряжения, выделяемые на индуктивности и емкости, так же равны друг другу по модулю и противоположны по знаку. Говорят, что в этом случае в контуре происходит резонанс напряжений, то есть суммарное падение напряжения на индуктивности и емкости равно нулю.
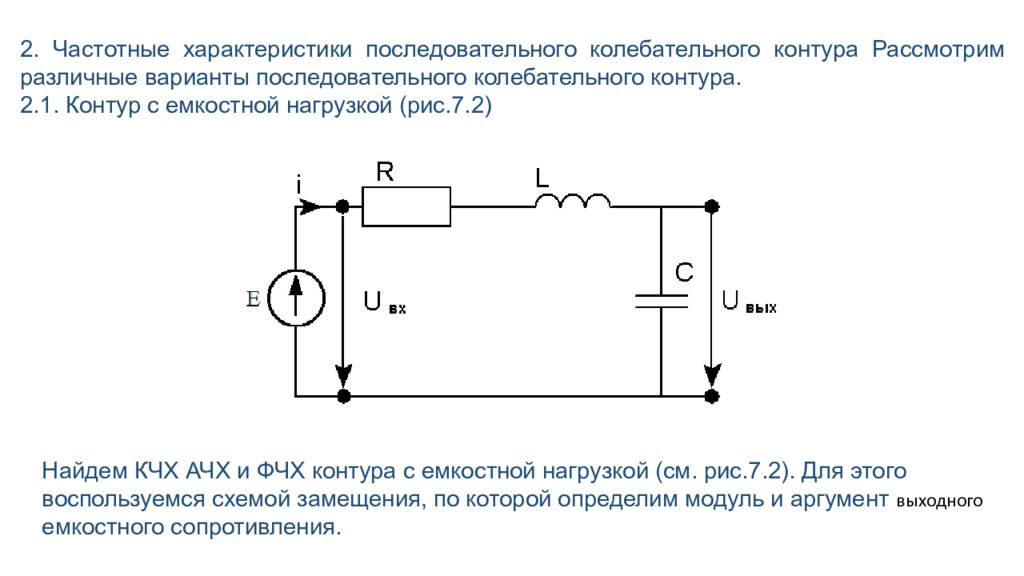
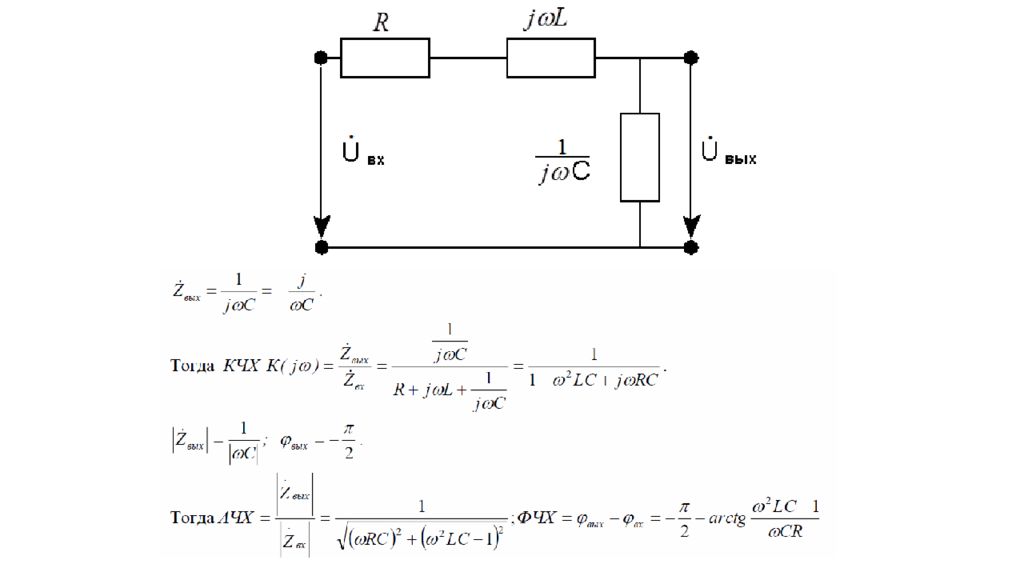
2. Частотные характеристики последовательного колебательного контура Рассмотрим различные варианты последовательного колебательного контура. 2.1. Контур с емкостной нагрузкой (рис.7.2) Найдем КЧХ АЧХ и ФЧХ контура с емкостной нагрузкой (см. рис.7.2). Для этого воспользуемся схемой замещения, по которой определим модуль и аргумент выходного емкостного сопротивления.
Одним из наиболее важных параметров колебательного контура является его характеристическое сопротивление. Характеристическим сопротивлением контура ρ называется величина модуля реактивного сопротивления емкости и индуктивности контура на резонансной частоте: В общем случае характеристическое сопротивление может быть вычислено по формуле: Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура: катушкой индуктивности (энергия магнитного поля) и конденсатором (энергия электрического поля).
Графики АЧХ и ФЧХ
АЧХ имеет max на резонансной частоте, т.к. входное сопротивление минимально и равно R. При этом ток протекающий в контуре, максимален и выходное напряжение также максимально. Обсудим изменение АЧХ при стремлении частоты к бесконечности. С увеличением частоты относительно резонансной АЧХ стремится к нулю, потому что емкость (конденсатор) закорачивает выходные клеммы с ростом частоты, поскольку емкостное сопротивление с ростом частоты уменьшается. Обсудим изменение АЧХ при стремлении частоты к нулю. При стремлении частоты к нулю значение АЧХ стремится к единице. Это можно объяснить так: - сопротивление конденсатора при стремлении частоты к нулю стремится к бесконечности, - тогда ток по цепи не течет, - падение напряжения на элементах R и L равно нулю, - следовательно, напряжения на входе и выходе одинаковы и их отношение равно единице.
Полосой пропускания линейной цепи называется диапазон частот, в котором АЧХ уменьшается не более, чем в раза от своего максимального значения. При увеличении R расширяется полоса пропускания последовательного колебательного контура. При высокой добротности полоса пропускания колебательного контура узкая, она пропускает частоты вблизи и контур называется полосно-пропускающим фильтром. С уменьшением добротности полоса пропускания контура расширяется, при добротности близкой к 1, контур станет фильтром низких частот. Изменяя индуктивность или емкость можем изменить резонансную частоту и сместить max АЧХ вправо ( L или C ↑ ) или влево ( L или C ↓ ) и изменим диапазон частот, которые пропускает фильтр.
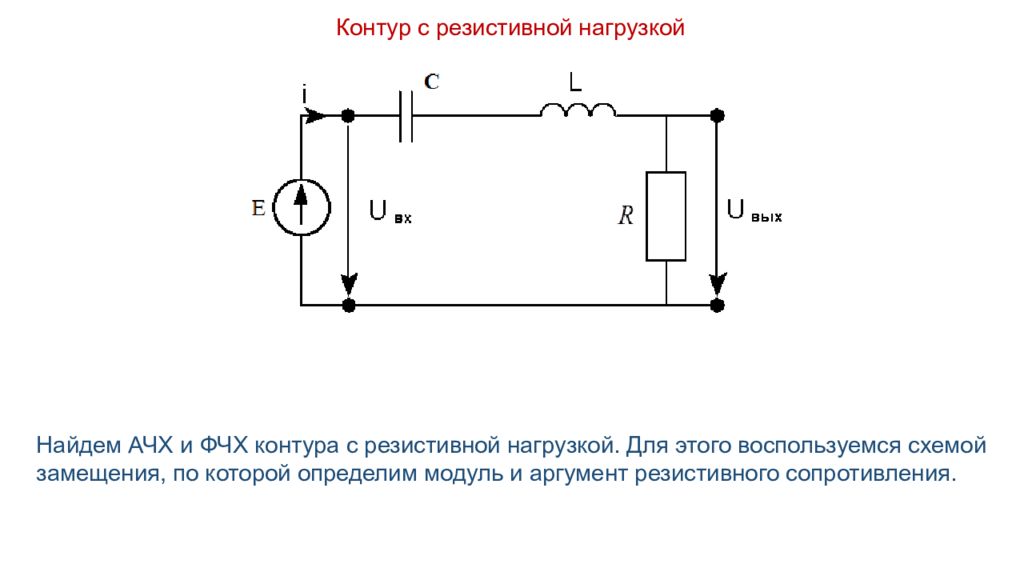
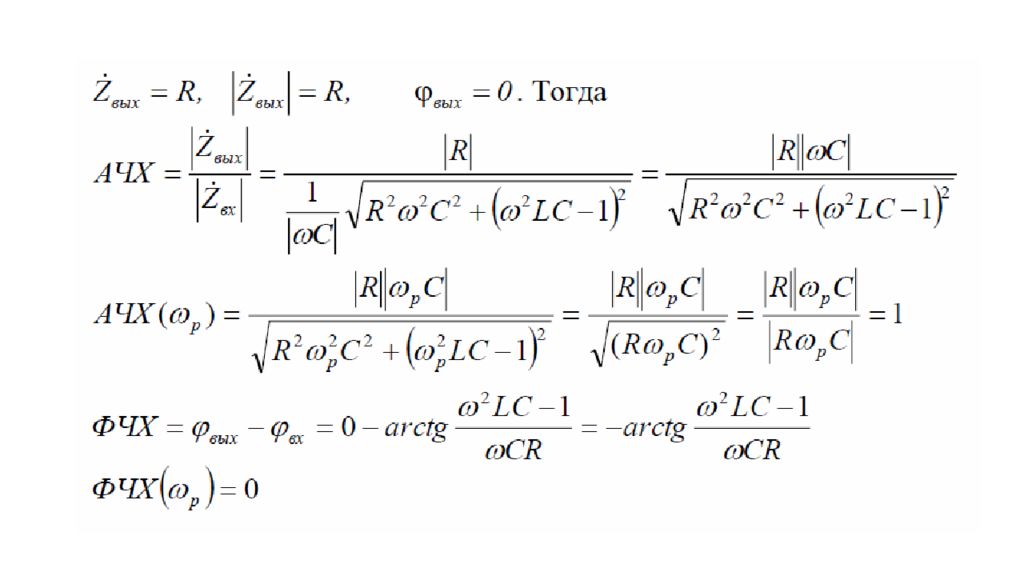
Контур с резистивной нагрузкой Найдем АЧХ и ФЧХ контура с резистивной нагрузкой. Для этого воспользуемся схемой замещения, по которой определим модуль и аргумент резистивного сопротивления.
Графики АЧХ и ФЧХ.
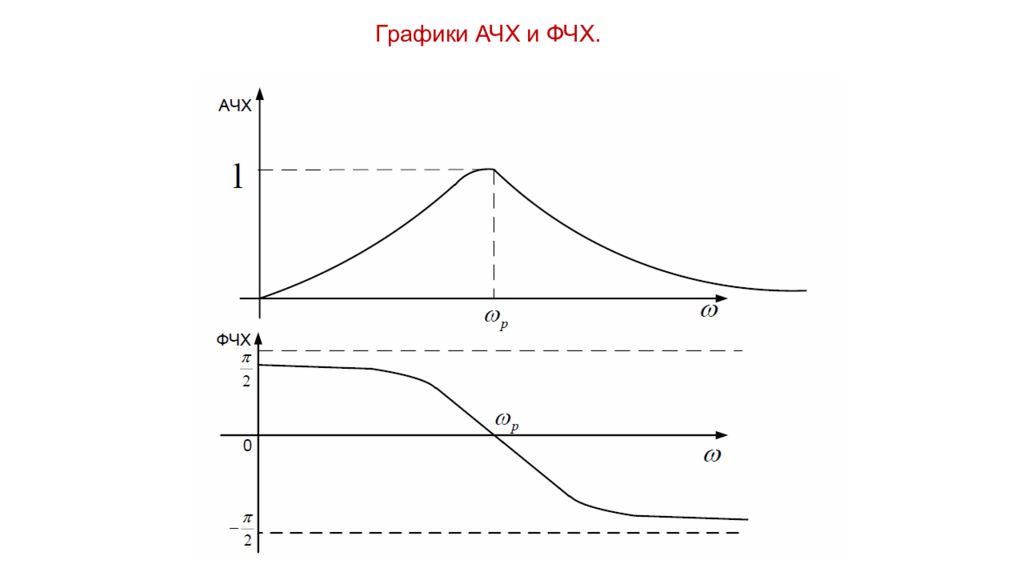
АЧХ имеет максимум на резонансной частоте, т.к. входное сопротивление минимально и равно R. При этом ток, протекающий по цепи, максимален и выходное напряжение также максимально. Изменение АЧХ при стремлении частоты к бесконечности. С увеличением частоты относительно резонансной АЧХ стремится к нулю, т.к. индуктивное сопротивление с ростом частоты стремится к бесконечности, ток через цепь стремится к нулю и напряжение на резистивной нагрузке (на выходе) также стремится к нулю. Изменение АЧХ при стремлении частоты к нулю. С уменьшением частоты относительно резонансной АЧХ стремится к нулю, т.к. емкостное сопротивление с ростом частоты стремится к бесконечности, ток через цепь опять стремится к нулю и напряжение на резистивной нагрузке (на выходе) также стремится к нулю.
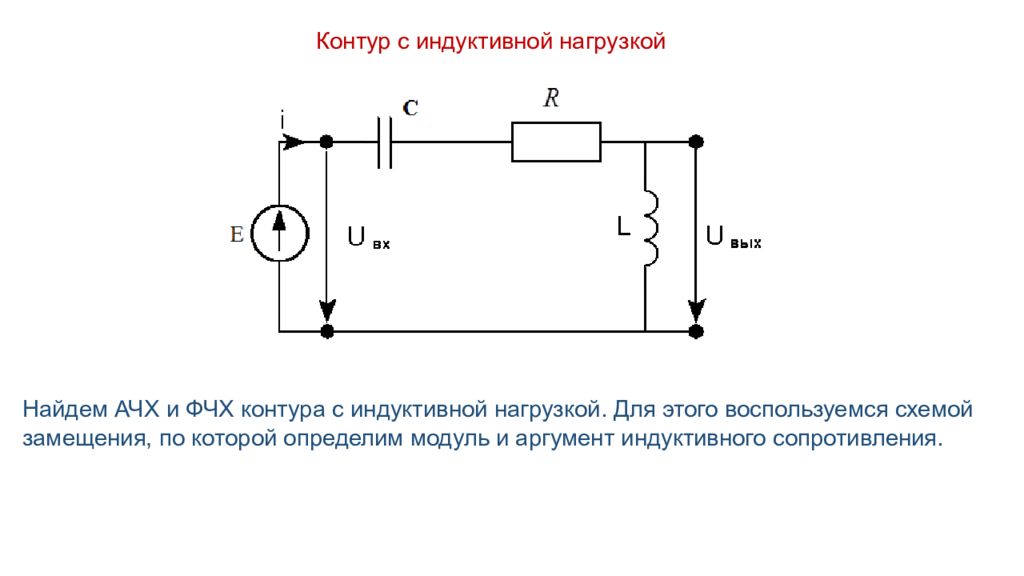
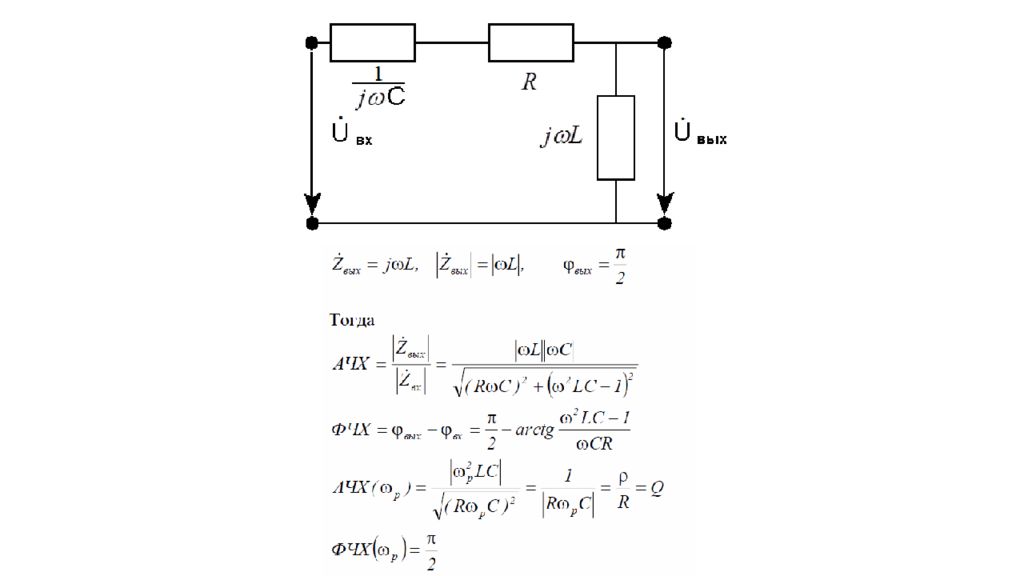
Контур с индуктивной нагрузкой Найдем АЧХ и ФЧХ контура с индуктивной нагрузкой. Для этого воспользуемся схемой замещения, по которой определим модуль и аргумент индуктивного сопротивления.
Графики АЧХ и ФЧХ последовательного колебательного контура с индуктивной нагрузкой
АЧХ имеет максимум на резонансной частоте, т.к. входное сопротивление минимально и равно R. При этом ток, протекающий по цепи, максимален и выходное напряжение также максимально. Изменение АЧХ при стремлении частоты к нулю. С уменьшением частоты относительно резонансной АЧХ стремится к нулю, это объясняется тем, что катушка индуктивности закорачивает выходные клеммы с уменьшением частоты, поскольку индуктивное сопротивление с уменьшением частоты уменьшается. Изменение АЧХ при стремлении частоты к бесконечности. При стремлении частоты к бесконечности значение АЧХ стремится к единице. Это можно объяснить так: - сопротивление индуктивности при стремлении частоты к бесконечности стремится к бесконечности, - тогда ток по цепи не течет, - падение напряжения на элементах R и С равно нулю, - следовательно, напряжения на входе и выходе одинаковы и их отношение равно единице.
