При двукратном бросании кости в сумме выпало 11 очков. Какова вероятность того, что хотя бы раз выпало 5 очков?
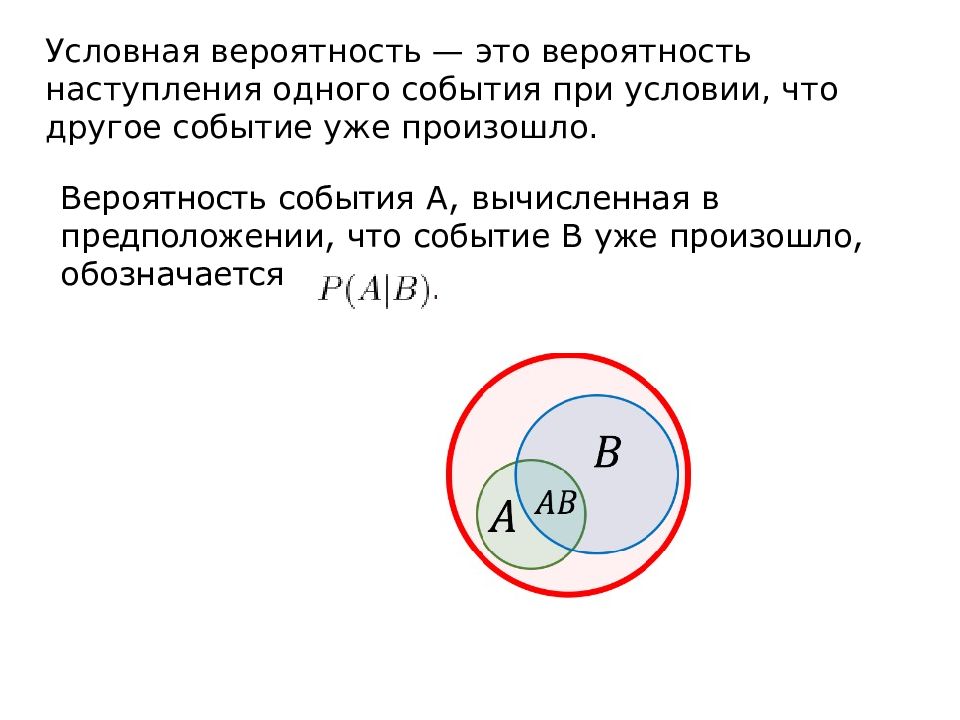
Условная вероятность — это вероятность наступления одного события при условии, что другое событие уже произошло. Вероятность события А, вычисленная в предположении, что событие В уже произошло, обозначается
Пусть для некоторого эксперимента красный круг обозначает множество всех возможных исходов. Зеленый круг обозначает множество исходов, благоприятствующих событию А, синий круг обозначает множество исходов, благоприятствующих событию В, область, лежащая в пересечении этих кругов обозначает множество исходов, благоприятствующих обоим событиям А и В, обозначим его АВ. Если мы вычисляем вероятность события А в предположении, что событие В уже произошло (то есть условную вероятность), то в этом случае для нас множество исходов, благоприятствующих событию В окажется множеством всех возможных исходов, а благоприятными исходами будут те исходы, которые при этом еще благоприятствуют событию А. То есть нам нужно найти, какую часть число исходов, благоприятствующих событиям А и В составляет от числа исходов, благоприятствующих событию В.
При двукратном бросании кости в сумме выпало 11 очков. Какова вероятность того, что хотя бы раз выпало 5 очков? При двукратном бросании игральной кости 11 очков может получится только в двух случаях: 6 + 5 и 5 + 6. При этом 5 очков выпадало в обоих случаях. Значит, вероятность того, что хотя бы раз выпало 5 очков равна
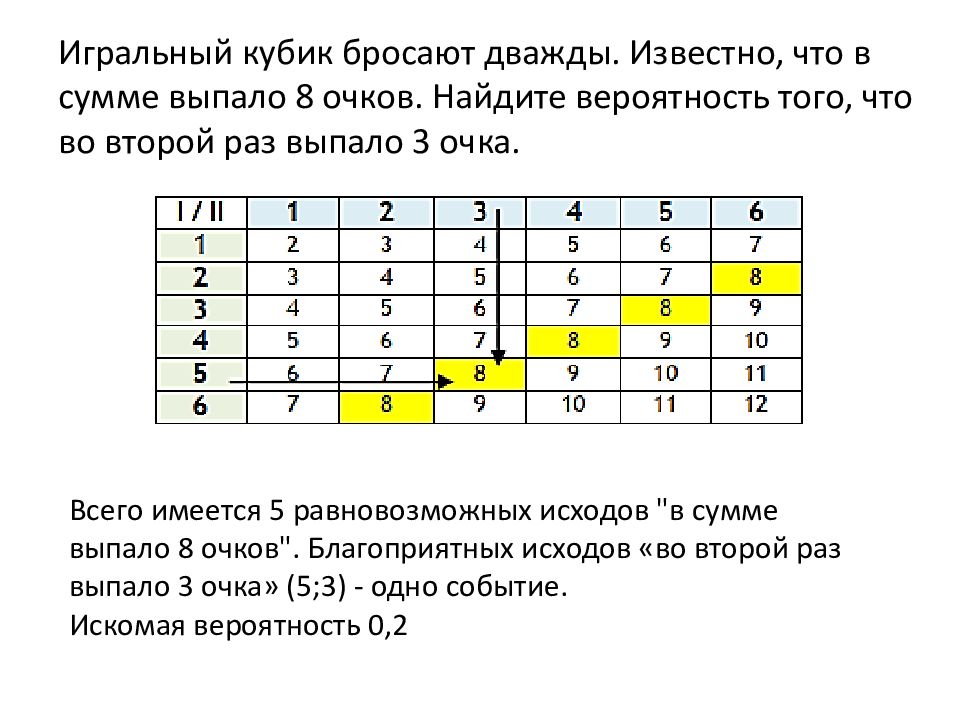
Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка. Всего имеется 5 равновозможных исходов " в сумме выпало 8 очков ". Благоприятных исходов «во второй раз выпало 3 очка » (5;3) - одно событие. Искомая вероятность 0,2
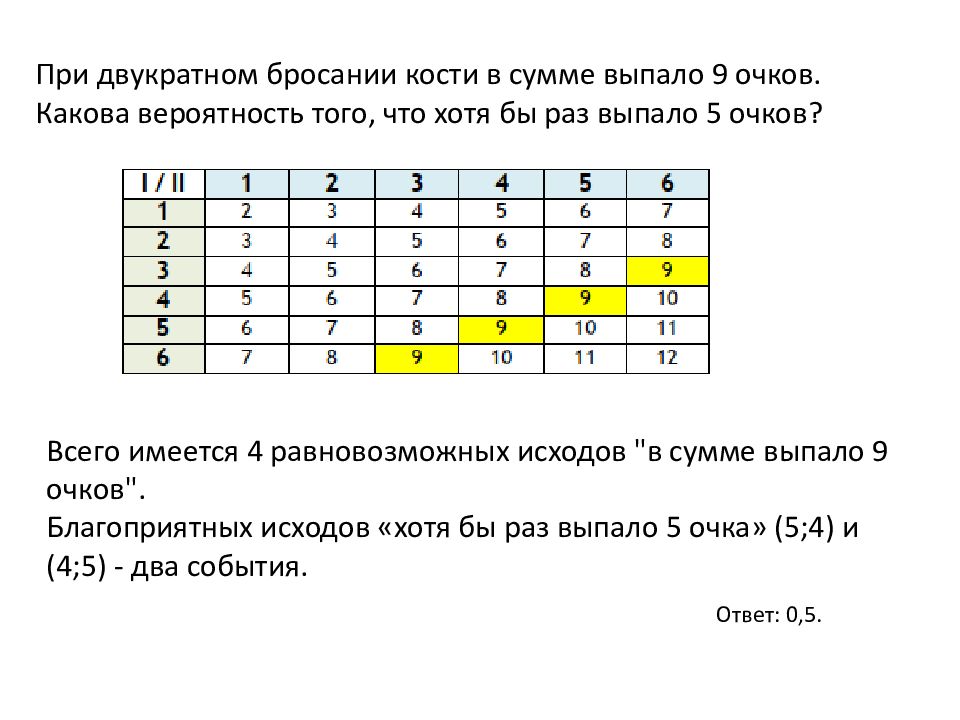
При двукратном бросании кости в сумме выпало 9 очков. Какова вероятность того, что хотя бы раз выпало 5 очков? Всего имеется 4 равновозможных исходов " в сумме выпало 9 очков". Благоприятных исходов «хотя бы раз выпало 5 очка » (5;4) и (4;5) - два события. Ответ: 0,5.
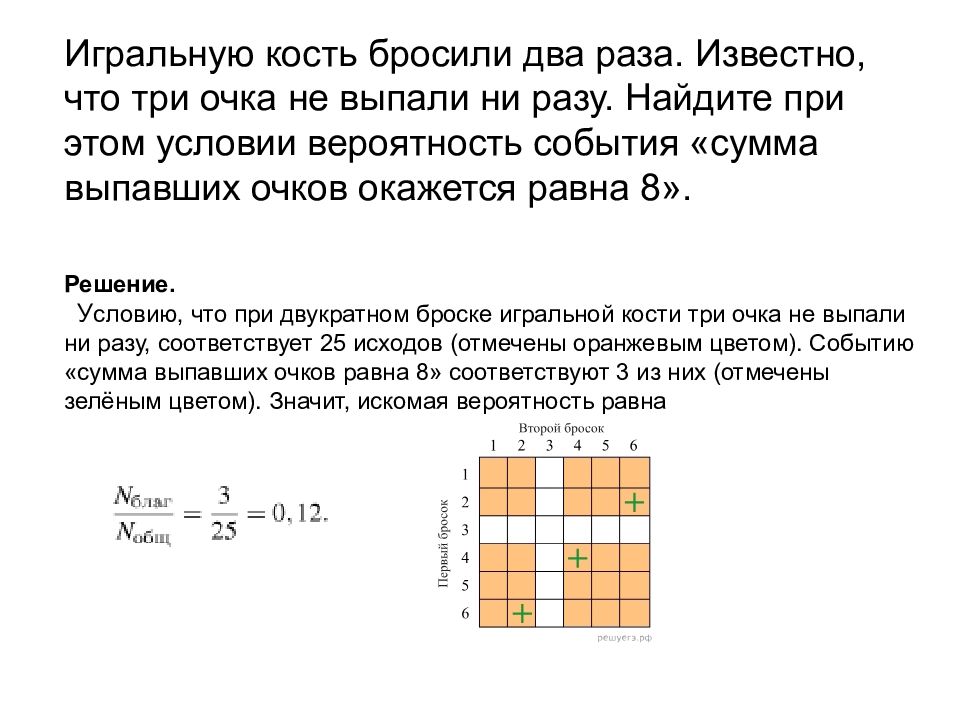
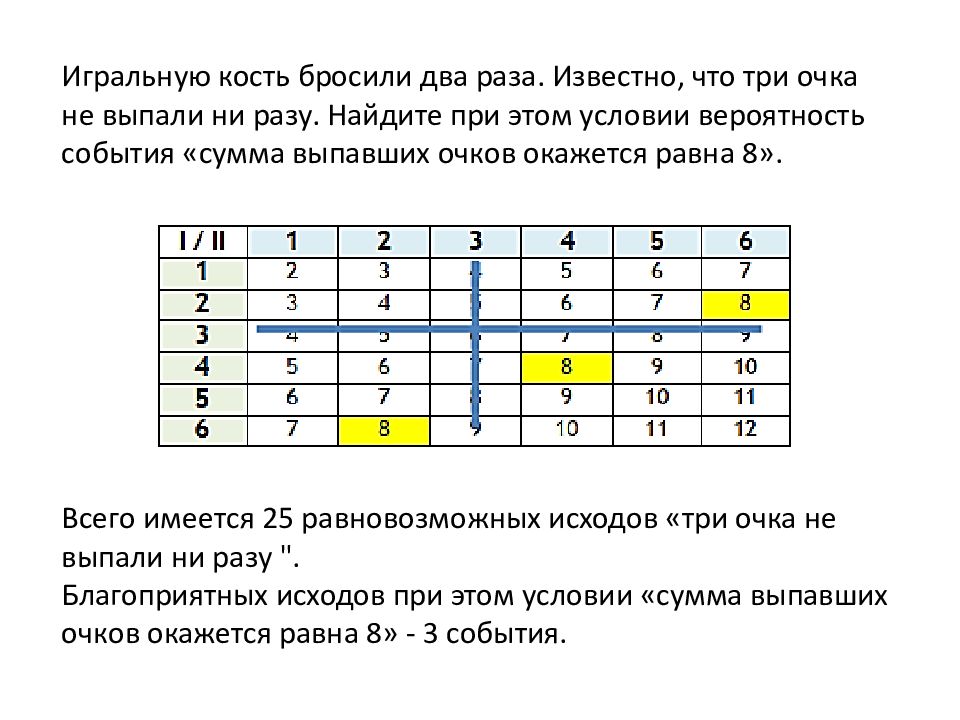
Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8». Решение. У словию, что при двукратном броске игральной кости три очка не выпали ни разу, соответствует 25 исходов (отмечены оранжевым цветом). Событию «сумма выпавших очков равна 8» соответствуют 3 из них (отмечены зелёным цветом). Значит, искомая вероятность равна
Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8». Всего имеется 25 равновозможных исходов « три очка не выпали ни разу ". Благоприятных исходов при этом условии « сумма выпавших очков окажется равна 8» - 3 события.
При двукратном бросании игральной кости в сумме выпало 8 очков. Какова вероятность того, что хотя бы раз выпало 6 очков?
Решение. При двукратном бросании игральной кости 3 очка может получится только в двух случаях: 1 + 2 и 2 + 1. При этом 2 очка выпадало в обоих случаях. Значит, вероятность того, что хотя бы раз выпало 2 очка равна При двукратном бросании игральной кости в сумме выпало 3 очка. Какова вероятность того, что хотя бы раз выпало 2 очка?
